Statistical Mechanics: Theory and Molecular Simulation Chapter 3 - The microcanonical ensemble and introduction to molecular dynamics

2023年4月3日 18:09

Statistical Mechanics: Theory and Molecular SimulationはMark Tuckermanによって著された分子シミュレーションに関連した熱・統計物理学，及び量子力学の参考書になります。

現時点では（恐らく）和訳がないこともあり，日本での知名度はあまりないような気がしますが，被引用数が1300を超えていることを考えると海外では高く認知されている参考書みたいです。

本記事では，Chapter 3（The microcanonical ensemble and introduction to molecular dynamics）の章末問題の和訳とその解答例を紹介します。解答例に間違いが見受けられた場合はお知らせいただけると助かります。

Problem 3.1

同一$${N}$$粒子からなる系の標準的なハミルトニアンを考える。

$$
\begin{align*}
\mathcal{H}&=\sum_{i=1}^N\frac{\mathbf{p}_i^2}{2m}+U(\mathbf{r}_1,\cdots,\mathbf{r}_N)
\end{align*}
$$

a. ミクロカノニカル分配関数が以下の数式で表現できることを示せ。

$$
\begin{align*}
\Omega(N,V,E)&=M_N\int{\rm d}E'\int{\rm d}^N\mathbf{p}\delta\left(\sum_{i=1}^N\frac{\mathbf{p}_i^2}{2m}-E'\right)\\
&\times\int_{D(V)}{\rm d}^N\mathbf{r}\delta\left(U(\mathbf{r}_1,\cdots,\mathbf{r}_N)-E+E'\right)
\end{align*}
$$

b. (a)の結果を用いて，分解関数が以下の数式で表現できることを示せ。

$$
\begin{align*}
\Omega(N,V,E)&=\frac{E_0}{N!\Gamma\left(\frac{3N}{2}\right)}\left[\left(\frac{2\pi m}{h^2}\right)^{3/2}\right]^N\\
&\times\int_{D(V)}{\rm d}^N\mathbf{r}\left[E-U(\mathbf{r}_1,\cdots,\mathbf{r}_N)\right]^{3N/2-1}\theta\left(E-U(\mathbf{r}_1,\cdots,\mathbf{r}_N)\right)
\end{align*}
$$

ここで，$${\theta(x)}$$はヘヴィサイドのステップ関数である。

a. デルタ関数の性質$${\int{\rm d}x\delta(x-a)\delta(x-b)=\delta(a-b)}$$を利用すると，

$$
\begin{align*}
\int{\rm d}E'\delta\left(\sum_{i=1}^N\frac{\mathbf{p}_i^2}{2m}-E'\right)\delta\left(U(\mathbf{r}_1,\cdots,\mathbf{r}_N)-E+E'\right)&=\int{\rm d}E'\delta\left(E'-\sum_{i=1}^N\frac{\mathbf{p}_i^2}{2m}\right)\delta\left(E'-\left(E-U(\mathbf{r}_1,\cdots,\mathbf{r}_N)\right)\right)\\
&=\delta\left(\sum_{i=1}^N\frac{\mathbf{p}_i^2}{2m}-\left(E-U(\mathbf{r}_1,\cdots,\mathbf{r}_N)\right)\right)\\
&=\delta\left(\mathcal{H}(\mathbf{x})-E\right)
\end{align*}
$$

となるため，

$$
\begin{align*}
\Omega(N,V,E)&=M_N\int{\rm d}^N\mathbf{p}\int_{D(V)}{\rm d}^N\mathbf{r}\delta\left(\mathcal{H}(\mathbf{x})-E\right)\\
&=M_N\int{\rm d}^N\mathbf{p}\int_{D(V)}{\rm d}^N\mathbf{r}\left\{\int{\rm d}E'\delta\left(\sum_{i=1}^N\frac{\mathbf{p}_i^2}{2m}-E'\right)\delta\left(U(\mathbf{r}_1,\cdots,\mathbf{r}_N)-E+E'\right)\right\}\\
&=M_N\int{\rm d}E'\int{\rm d}^N\mathbf{p}\delta\left(\sum_{i=1}^N\frac{\mathbf{p}_i^2}{2m}-E'\right)\int_{D(V)}{\rm d}^N\mathbf{r}\delta\left(U(\mathbf{r}_1,\cdots,\mathbf{r}_N)-E+E'\right)
\end{align*}
$$

b. 運動量に関する積分は本文の式(3.5.18)の結果を天下り的に利用して，

$$
\begin{align*}
M_N\int{\rm d}^N\mathbf{p}\delta\left(\sum_{i=1}^N\frac{\mathbf{p}_i^2}{2m}-E'\right)&=\frac{E_0}{E'}\frac{1}{N!}\frac{1}{\Gamma(3N/2)}\left(\frac{2\pi mE'}{h^2}\right)^{3N/2}
\end{align*}
$$

と計算される。
さらに$${E\geq U(\mathbf{r}_1,\cdots,\mathbf{r}_N)}$$であることに注意して$${E'}$$に関する積分を実行することにより，

$$
\begin{align*}
\Omega(N,V,E)&=\frac{E_0}{N!\Gamma(3N/2)}\left(\frac{2\pi m}{h^2}\right)^{3N/2}\int_{D(V)}{\rm d}^N\mathbf{r}\left[\int{\rm d}E' (E')^{3N/2-1}\delta\left(U(\mathbf{r}_1,\cdots,\mathbf{r}_N)-E+E'\right)\right]\\
&=\frac{E_0}{N!\Gamma(3N/2)}\left(\frac{2\pi m}{h^2}\right)^{3N/2}\int_{D(V)}{\rm d}^N\mathbf{r}\left[E-U(\mathbf{r}_1,\cdots,\mathbf{r}_N)\right]^{3N/2-1}\theta\left(E-U(\mathbf{r}_1,\cdots,\mathbf{r}_N)\right)
\end{align*}
$$

Problem 3.2

1.7節の図1.7にて記されている調和ポリマーモデルの例を取り扱う。

全ての結合長の平衡値が0であるとき，ポテンシャルエネルギーは以下の式で表される。

$$
\begin{align*}
U(\mathbf{r}_0,\cdots,\mathbf{r}_{N+1})&=\frac{1}{2}m\omega^2\sum_{k=0}^N(\mathbf{r}_k-\mathbf{r}_{k+1})^2
\end{align*}
$$

ここで$${m}$$は粒子の質量，$${\omega}$$は調和カップリングの振動数である。両端の座標をそれぞれ$${\mathbf{r},\ \mathbf{r}'}$$と表記することにする，つまり$${\mathbf{r}:=\mathbf{r}_0,\ \mathbf{r}':=\mathbf{r}_{N+1}}$$である。
以下の座標変換を考える。

$$
\begin{align*}
\mathbf{r}_k&=\mathbf{u}_k+\frac{k}{k+1}\mathbf{r}_{k+1}+\frac{1}{k+1}\mathbf{r},\ \ \ \ \ \ k=1,\cdots,N
\end{align*}
$$

この座標変換を利用することにより，系のミクロカノニカル分配関数$${\Omega(N,V,E)}$$を計算せよ。ポリマーは体積$${V}$$の立方体の中に存在すると仮定せよ。
ヒント：変換は再帰的に実行する必要があることに注意せよ。再帰をどのように実行すべきだろうか？$${N=2, 3}$$といった少数の場合にどうなるかを具体的に調べることが有効かもしれない。

式(4.5.44)より，ポテンシャルエネルギーは

$$
\begin{align*}
U(\mathbf{u}_1,\cdots,\mathbf{u}_{N},\mathbf{r},\mathbf{r}')&=\frac{1}{2}m\omega^2\sum_{k=0}^N(\mathbf{r}_k-\mathbf{r}_{k+1})^2\\
&=\sum_{k=1}^N\frac{(k+1)m\omega^2}{2k}\mathbf{u}_k^2+\frac{m\omega^2}{2(N+1)}(\mathbf{r}-\mathbf{r}')^2
\end{align*}
$$

と変形できる。また，式(4.5.46)より変換のヤコビアンは1である。

$$
\begin{align*}
{\rm d}^N\mathbf{r}&={\rm d}^N\mathbf{u}
\end{align*}
$$

以上の踏まえて，ミクロカノニカル分配関数を式展開すると，

$$
\begin{align*}
\Omega(N+2,V,E)&=\frac{E_0}{h^{3(N+2)}}\int{\rm d}\mathbf{r}\int{\rm d}\mathbf{r}'\int{\rm d}^{N+2}\mathbf{p}\int{\rm d}^N\mathbf{r}\delta\left(\frac{1}{2m}\sum_{k=0}^{N+1}\mathbf{p}_k^2+\frac{1}{2}m\omega^2\sum_{k=0}^N(\mathbf{r}_k-\mathbf{r}_{k+1})^2-E\right)\\
&=\frac{E_0}{h^{3(N+2)}}\int{\rm d}\mathbf{r}\int{\rm d}\mathbf{r}'\int{\rm d}^{N+2}\mathbf{p}\int{\rm d}^N\mathbf{u}\delta\left(\sum_{k=1}^N\left\{\frac{\mathbf{p}_k^2}{2m}+\frac{(k+1)m\omega^2}{2k}\mathbf{u}_k^2\right\}+\frac{1}{2m}(\mathbf{p}_0^2+\mathbf{p}_{N+1}^{2})-\left\{E-\frac{m\omega^2}{2(N+1)}(\mathbf{r}-\mathbf{r}')^2\right\}\right)\\
&=E_0(N+1)^{3/2}\left(\frac{2}{2\pi\hbar\omega}\right)^{3(N+2)}\int{\rm d}\mathbf{r}\int{\rm d}\mathbf{r}'\int{\rm d}^{N+2}\mathbf{p}\int{\rm d}^{N}\mathbf{u}\delta\left(\sum_{k=1}^N\left(\mathbf{p}_k^2+\mathbf{u}_k^2\right)+(\mathbf{p}_0^2+\mathbf{p}_{N+1}^{2})-\left\{E-(\mathbf{r}-\mathbf{r}')^2\right\}\right)\\
&=:E_0(N+1)^{3/2}\left(\frac{2}{2\pi\hbar\omega}\right)^{3(N+2)}\int{\rm d}\mathbf{r}\int{\rm d}\mathbf{r}'\int{\rm d}^{N+2}\mathbf{p}\int{\rm d}^{N}\mathbf{u}\delta\left(\sum_{k=1}^N\left(\mathbf{p}_k^2+\mathbf{u}_k^2\right)+(\mathbf{p}_0^2+\mathbf{p}_{N+1}^{2})-E'(\mathbf{r},\mathbf{r}')\right)\\
&=\frac{E_0(N+1)^{3/2}}{(2\pi)^3\Gamma(3(N+1))}\left(\frac{2}{\hbar\omega}\right)^{3(N+2)}\int{\rm d}\mathbf{r}\int{\rm d}\mathbf{r}'\int_{0}^{\infty}{\rm d}RR^{6N+5}\delta\left(R^2-E'(\mathbf{r},\mathbf{r}')\right)\\
&=\frac{E_0(N+1)^{3/2}}{(2\pi)^3\Gamma(3(N+1))}\left(\frac{2}{\hbar\omega}\right)^{3(N+2)}\int{\rm d}\mathbf{r}\int{\rm d}\mathbf{r}'\frac{1}{2\sqrt{E'}}\int_{0}^{\infty}{\rm d}RR^{6N+5}\delta\left(R-\sqrt{E'}\right)\\
&=\frac{E_0(N+1)^{3/2}}{2(2\pi)^3\Gamma(3(N+1))}\left(\frac{2}{\hbar\omega}\right)^{3(N+2)}\int{\rm d}\mathbf{r}\int{\rm d}\mathbf{r}'\left\{E-(\mathbf{r}-\mathbf{r}')^2\right\}^{3N+2}\\
&=\frac{E_0Vm^{3/2}\omega^3}{2^{5/2}(2\pi)^3\Gamma(3(N+1))}\left(\frac{2}{\hbar\omega}\right)^{3(N+2)}\int{\rm d}\mathbf{s}\left(E-\mathbf{s}^2\right)^{3N+2}\\
&=\frac{E_0Vm^{3/2}\omega^3}{2^{5/2}(2\pi)^3\Gamma(3(N+1))}\left(\frac{2}{\hbar\omega}\right)^{3(N+2)}\int_{0}^{\sqrt{E}}{\rm d}s s^2(E-s^2)^{3N+2}\\
&=\frac{E_0Vm^{3/2}\omega^3}{2^{5/2}(2\pi)^3}\left(\frac{2}{\hbar\omega}\right)^{3(N+2)}\frac{2^{3N+2}E^{\frac{6N+7}{2}}}{(6N+7)!!}\\
\end{align*}
$$

となる。

Problem 3.3

外部ポテンシャル下にある単一の水分子$${\rm H_2O}$$を考える。３原子の座標をそれぞれ$${\mathbf{r}_{\rm O},\ \mathbf{r}_{\rm H_1},\ \mathbf{r}_{\rm H_2}}$$，及び作用する力をそれぞれ$${\mathbf{F}_{\rm O},\ \mathbf{F}_{\rm H_1},\ \mathbf{F}_{\rm H_2}}$$と表すことにする。分子を結合長$${d_{\rm OH},\ d_{\rm HH}}$$が固定された剛体として扱い，以下の拘束条件を課すことにする。

$$
\begin{align*}
|\mathbf{r}_{\rm O}- \mathbf{r}_{\rm H_1}|^2-d_{\rm OH}^2&=0\\
|\mathbf{r}_{\rm O}- \mathbf{r}_{\rm H_2}|^2-d_{\rm OH}^2&=0\\
|\mathbf{r}_{\rm H_1}- \mathbf{r}_{\rm H_2}|^2-d_{\rm HH}^2&=0\\
\end{align*}
$$

a. ラグランジュの未定乗数法を用いて，3原子に対する拘束条件付きの運動方程式を導け。

b. 運動方程式を速度ベルレ法を用いて数値積分することを考える。SHAKEステップにおける係数を解くために使用される3x3の行列方程式を導け。

c. 線形化された行列方程式を解くための反復法を考案せよ。

d. RATTLEステップにおける係数を解くために使用される3x3の行列方程式を導け。この方程式は反復することなく解析的に解くことができることを示せ。

a. $${\rm O}$$原子の質量を$${m_{\rm O}}$$，$${\rm H}$$原子の質量を$${m_{\rm H}}$$とする。また，拘束条件を

$$
\begin{align*}
\sigma_1(\mathbf{r}_{\rm O},\mathbf{r}_{\rm H_1})&:=|\mathbf{r}_{\rm O}- \mathbf{r}_{\rm H_1}|^2-d_{\rm OH}^2\\
\sigma_2(\mathbf{r}_{\rm O},\mathbf{r}_{\rm H_2})&:=|\mathbf{r}_{\rm O}- \mathbf{r}_{\rm H_2}|^2-d_{\rm OH}^2\\
\sigma_3(\mathbf{r}_{\rm H_1},\mathbf{r}_{\rm H_2})&:=|\mathbf{r}_{\rm H_1}- \mathbf{r}_{\rm H_2}|^2-d_{\rm HH}^2
\end{align*}
$$

とし，対応する未定乗数をそれぞれ$${\lambda_1,\ \lambda_2,\ \lambda_3}$$とする。
このとき，３原子の拘束条件付きの運動方程式は以下の通りとなる。

$$
\begin{align*}
m_{\rm O}\ddot{\mathbf{r}}_{\rm O}&=\mathbf{F}_{\rm O}+2\lambda_1(\mathbf{r}_{\rm O}- \mathbf{r}_{\rm H_1})+2\lambda_2(\mathbf{r}_{\rm O}- \mathbf{r}_{\rm H_2})\\
m_{\rm H}\ddot{\mathbf{r}}_{\rm H_1}&=\mathbf{F}_{\rm H_1}-2\lambda_1(\mathbf{r}_{\rm O}- \mathbf{r}_{\rm H_1})+2\lambda_3(\mathbf{r}_{\rm H_1}- \mathbf{r}_{\rm H_2})\\
m_{\rm H}\ddot{\mathbf{r}}_{\rm H_2}&=\mathbf{F}_{\rm H_2}-2\lambda_1(\mathbf{r}_{\rm O}- \mathbf{r}_{\rm H_2})-2\lambda_3(\mathbf{r}_{\rm H_1}- \mathbf{r}_{\rm H_2})
\end{align*}
$$

b. 速度ベルレ法を用いて$${t=0}$$から$${t=\Delta t}$$の時間発展に対して各座標を更新すると，

$$
\begin{align*}
\mathbf{r}_{\rm O}(\Delta t)&=\mathbf{r}_{\rm O}(0)+\Delta t \mathbf{v}_{\rm O}(0)+\frac{\Delta t^2}{2m_{\rm O}}\mathbf{F}_{\rm O}+\frac{\Delta t^2}{m_{\rm O}}\left\{\lambda_1(\mathbf{r}_{\rm O}(0)- \mathbf{r}_{\rm H_1}(0))+\lambda_2(\mathbf{r}_{\rm O}(0)- \mathbf{r}_{\rm H_2}(0))\right\}\\
&=:\mathbf{r}_{\rm O}'+\frac{1}{m_{\rm O}}\left\{\tilde{\lambda}_1(\mathbf{r}_{\rm O}(0)- \mathbf{r}_{\rm H_1}(0))+\tilde{\lambda}_2(\mathbf{r}_{\rm O}(0)- \mathbf{r}_{\rm H_2}(0))\right\}\\
\mathbf{r}_{\rm H_1}(\Delta t)&=\mathbf{r}_{\rm H_1}(0)+\Delta t \mathbf{v}_{\rm H_1}(0)+\frac{\Delta t^2}{2m_{\rm H}}\mathbf{F}_{\rm H_1}+\frac{\Delta t^2}{m_{\rm H}}\left\{-\lambda_1(\mathbf{r}_{\rm O}(0)- \mathbf{r}_{\rm H_1}(0))+\lambda_3(\mathbf{r}_{\rm H_1}(0)- \mathbf{r}_{\rm H_2})(0)\right\}\\
&=:\mathbf{r}_{\rm H_1}'+\frac{1}{m_{\rm H}}\left\{-\tilde{\lambda}_1(\mathbf{r}_{\rm O}(0)- \mathbf{r}_{\rm H_1}(0))+\tilde{\lambda}_3(\mathbf{r}_{\rm H_1}(0)- \mathbf{r}_{\rm H_2}(0))\right\}\\
\mathbf{r}_{\rm H_2}(\Delta t)&=\mathbf{r}_{\rm H_2}(0)+\Delta t \mathbf{v}_{\rm H_2}(0)+\frac{\Delta t^2}{2m_{\rm H}}\mathbf{F}_{\rm H_2}+\frac{\Delta t^2}{m_{\rm H}}\left\{-\lambda_2(\mathbf{r}_{\rm O}(0)- \mathbf{r}_{\rm H_2}(0))-\lambda_3(\mathbf{r}_{\rm H_1}(0)- \mathbf{r}_{\rm H_2})(0)\right\}\\
&=:\mathbf{r}_{\rm H_2}'+\frac{1}{m_{\rm H}}\left\{-\tilde{\lambda}_2(\mathbf{r}_{\rm O}(0)- \mathbf{r}_{\rm H_2}(0))-\tilde{\lambda}_3(\mathbf{r}_{\rm H_1}(0)- \mathbf{r}_{\rm H_2}(0))\right\}\\
\end{align*}
$$

ここで，$${\tilde{\lambda}_i=\tilde{\lambda}_i^{(1)}+\delta \tilde{\lambda}_i^{(1)}}$$とし，また，

$$
\begin{align*}
\mathbf{r}_{\rm O}^{(1)}&:=\mathbf{r}_{\rm O}'+\frac{1}{m_{\rm O}}\left\{\tilde{\lambda}_1^{(1)}(\mathbf{r}_{\rm O}(0)- \mathbf{r}_{\rm H_1}(0))+\tilde{\lambda}_2^{(1)}(\mathbf{r}_{\rm O}(0)- \mathbf{r}_{\rm H_2}(0))\right\}\\
\mathbf{r}_{\rm H_1}^{(1)}&:=\mathbf{r}_{\rm H_1}'+\frac{1}{m_{\rm H}}\left\{-\tilde{\lambda}_1^{(1)}(\mathbf{r}_{\rm O}(0)- \mathbf{r}_{\rm H_1}(0))+\tilde{\lambda}_3^{(1)}(\mathbf{r}_{\rm H_1}(0)- \mathbf{r}_{\rm H_2}(0))\right\}\\
\mathbf{r}_{\rm H_2}^{(1)}&:=\mathbf{r}_{\rm H_2}'+\frac{1}{m_{\rm H}}\left\{-\tilde{\lambda}_2^{(1)}(\mathbf{r}_{\rm O}(0)- \mathbf{r}_{\rm H_2}(0))-\tilde{\lambda}_3^{(1)}(\mathbf{r}_{\rm H_1}(0)- \mathbf{r}_{\rm H_2}(0))\right\}\\
\end{align*}
$$

と定義する。
$${t=\Delta t}$$における拘束条件を$${\delta\tilde{\lambda}_i}$$の一次で近似すると，

$$
\begin{align*}
\sigma_1(\mathbf{r}_{\rm O}(\Delta t),\mathbf{r}_{\rm H_1}(\Delta t))&=|\mathbf{r}_{\rm O}(\Delta t)- \mathbf{r}_{\rm H_1}(\Delta t)|^2-d_{\rm OH}^2\\
&=\left|\left[\mathbf{r}_{\rm O}^{(1)}+\frac{1}{m_{\rm O}}\left\{\delta\tilde{\lambda}_1^{(1)}(\mathbf{r}_{\rm O}(0)- \mathbf{r}_{\rm H_1}(0))+\delta\tilde{\lambda}_2^{(1)}(\mathbf{r}_{\rm O}(0)- \mathbf{r}_{\rm H_2}(0))\right\}\right]- \left[\mathbf{r}_{\rm H_1}^{(1)}+\frac{1}{m_{\rm H}}\left\{-\delta\tilde{\lambda}_1^{(1)}(\mathbf{r}_{\rm O}(0)- \mathbf{r}_{\rm H_1}(0))+\delta\tilde{\lambda}_3^{(1)}(\mathbf{r}_{\rm H_1}(0)- \mathbf{r}_{\rm H_2}(0))\right\}\right]\right|^2-d_{\rm OH}^2\\
&\simeq \sigma_1\left(\mathbf{r}_{\rm O}^{(1)},\mathbf{r}_{\rm H_1}^{(1)}\right)+2\left(\mathbf{r}_{\rm O}^{(1)}-\mathbf{r}_{\rm H_1}^{(1)}\right)\left\{\left(\frac{1}{m_{\rm O}}+\frac{1}{m_{\rm H}}\right)(\mathbf{r}_{\rm O}(0)- \mathbf{r}_{\rm H_1}(0))\right\}\delta\tilde{\lambda}_1^{(1)}+2\left(\mathbf{r}_{\rm O}^{(1)}-\mathbf{r}_{\rm H_1}^{(1)}\right)\frac{1}{m_{\rm O}}(\mathbf{r}_{\rm O}(0)- \mathbf{r}_{\rm H_2}(0))\delta\tilde{\lambda}_2^{(1)}-2\left(\mathbf{r}_{\rm O}^{(1)}-\mathbf{r}_{\rm H_1}^{(1)}\right)\frac{1}{m_{\rm H}}(\mathbf{r}_{\rm H_1}(0)- \mathbf{r}_{\rm H_2}(0))\delta\tilde{\lambda}_3^{(1)}\\
&=0\\
\sigma_2(\mathbf{r}_{\rm O}(\Delta t),\mathbf{r}_{\rm H_2}(\Delta t))&=|\mathbf{r}_{\rm O}(\Delta t)- \mathbf{r}_{\rm H_2}(\Delta t)|^2-d_{\rm OH}^2\\
&=\left|\left[\mathbf{r}_{\rm O}^{(1)}+\frac{1}{m_{\rm O}}\left\{\delta\tilde{\lambda}_1^{(1)}(\mathbf{r}_{\rm O}(0)- \mathbf{r}_{\rm H_1}(0))+\delta\tilde{\lambda}_2^{(1)}(\mathbf{r}_{\rm O}(0)- \mathbf{r}_{\rm H_2}(0))\right\}\right]- \left[\mathbf{r}_{\rm H_2}^{(1)}+\frac{1}{m_{\rm H}}\left\{-\delta\tilde{\lambda}_2^{(1)}(\mathbf{r}_{\rm O}(0)- \mathbf{r}_{\rm H_2}(0))-\delta\tilde{\lambda}_3^{(1)}(\mathbf{r}_{\rm H_1}(0)- \mathbf{r}_{\rm H_2}(0))\right\}\right]\right|^2-d_{\rm OH}^2\\
&\simeq \sigma_2\left(\mathbf{r}_{\rm O}^{(1)},\mathbf{r}_{\rm H_2}^{(1)}\right)+2\left(\mathbf{r}_{\rm O}^{(1)}-\mathbf{r}_{\rm H_2}^{(1)}\right)\frac{1}{m_{\rm O}}(\mathbf{r}_{\rm O}(0)- \mathbf{r}_{\rm H_1}(0))\delta\tilde{\lambda}_1^{(1)}+2\left(\mathbf{r}_{\rm O}^{(1)}-\mathbf{r}_{\rm H_2}^{(1)}\right)\left\{\left(\frac{1}{m_{\rm O}}+\frac{1}{m_{\rm H}}\right)(\mathbf{r}_{\rm O}(0)- \mathbf{r}_{\rm H_2}(0))\right\}\delta\tilde{\lambda}_2^{(1)}+2\left(\mathbf{r}_{\rm O}^{(1)}-\mathbf{r}_{\rm H_2}^{(1)}\right)\frac{1}{m_{\rm H}}(\mathbf{r}_{\rm H_1}(0)- \mathbf{r}_{\rm H_2}(0))\delta\tilde{\lambda}_3^{(1)}\\
&=0\\
\sigma_3(\mathbf{r}_{\rm H_1}(\Delta t),\mathbf{r}_{\rm H_2}(\Delta t))&=|\mathbf{r}_{\rm H_1}(\Delta t)- \mathbf{r}_{\rm H_2}(\Delta t)|^2-d_{\rm HH}^2\\
&=\left|\left[\mathbf{r}_{\rm H_1}^{(1)}+\frac{1}{m_{\rm H}}\left\{-\delta\tilde{\lambda}_1^{(1)}(\mathbf{r}_{\rm O}(0)- \mathbf{r}_{\rm H_1}(0))+\delta\tilde{\lambda}_3^{(1)}(\mathbf{r}_{\rm H_1}(0)- \mathbf{r}_{\rm H_2}(0))\right\}\right]- \left[\mathbf{r}_{\rm H_2}^{(1)}+\frac{1}{m_{\rm H}}\left\{-\delta\tilde{\lambda}_2^{(1)}(\mathbf{r}_{\rm O}(0)- \mathbf{r}_{\rm H_2}(0))-\delta\tilde{\lambda}_3^{(1)}(\mathbf{r}_{\rm H_1}(0)- \mathbf{r}_{\rm H_2}(0))\right\}\right]\right|^2-d_{\rm OH}^2\\
&\simeq \sigma_3\left(\mathbf{r}_{\rm H_1}^{(1)},\mathbf{r}_{\rm H_2}^{(1)}\right)-2\left(\mathbf{r}_{\rm H_1}^{(1)}-\mathbf{r}_{\rm H_2}^{(1)}\right)\frac{1}{m_{\rm H}}(\mathbf{r}_{\rm O}(0)- \mathbf{r}_{\rm H_1}(0))\delta\tilde{\lambda}_1^{(1)}+2\left(\mathbf{r}_{\rm H_1}^{(1)}-\mathbf{r}_{\rm H_2}^{(1)}\right)\frac{1}{m_{\rm H}}(\mathbf{r}_{\rm O}(0)- \mathbf{r}_{\rm H_2}(0))\delta\tilde{\lambda}_2^{(1)}+2\left(\mathbf{r}_{\rm H_1}^{(1)}-\mathbf{r}_{\rm H_2}^{(1)}\right)\frac{2}{m_{\rm H}}(\mathbf{r}_{\rm H_1}(0)- \mathbf{r}_{\rm H_2}(0))\delta\tilde{\lambda}_3^{(1)}\\
&=0\\
\end{align*}
$$

$$
\begin{align*}
\therefore \begin{bmatrix}\delta\tilde{\lambda}_1^{(1)} \\ \delta\tilde{\lambda}_2^{(1)}\\\delta\tilde{\lambda}_3^{(1)}\end{bmatrix}&=\frac{1}{2}\begin{bmatrix}\left(\mathbf{r}_{\rm O}^{(1)}-\mathbf{r}_{\rm H_1}^{(1)}\right)\left(\frac{1}{m_{\rm O}}+\frac{1}{m_{\rm H}}\right)(\mathbf{r}_{\rm O}(0)- \mathbf{r}_{\rm H_1}(0))&\left(\mathbf{r}_{\rm O}^{(1)}-\mathbf{r}_{\rm H_1}^{(1)}\right)\frac{1}{m_{\rm O}}(\mathbf{r}_{\rm O}(0)- \mathbf{r}_{\rm H_2}(0))&-\left(\mathbf{r}_{\rm O}^{(1)}-\mathbf{r}_{\rm H_1}^{(1)}\right)\frac{1}{m_{\rm H}}(\mathbf{r}_{\rm H_1}(0)- \mathbf{r}_{\rm H_2}(0))\\
\left(\mathbf{r}_{\rm O}^{(1)}-\mathbf{r}_{\rm H_2}^{(1)}\right)\frac{1}{m_{\rm O}}(\mathbf{r}_{\rm O}(0)- \mathbf{r}_{\rm H_1}(0))&\left(\mathbf{r}_{\rm O}^{(1)}-\mathbf{r}_{\rm H_2}^{(1)}\right)\left(\frac{1}{m_{\rm O}}+\frac{1}{m_{\rm H}}\right)(\mathbf{r}_{\rm O}(0)- \mathbf{r}_{\rm H_2}(0))& \left(\mathbf{r}_{\rm O}^{(1)}-\mathbf{r}_{\rm H_2}^{(1)}\right)\frac{1}{m_{\rm H}}(\mathbf{r}_{\rm H_1}(0)- \mathbf{r}_{\rm H_2}(0))\\
-\left(\mathbf{r}_{\rm H_1}^{(1)}-\mathbf{r}_{\rm H_2}^{(1)}\right)\frac{1}{m_{\rm H}}(\mathbf{r}_{\rm O}(0)- \mathbf{r}_{\rm H_1}(0))&\left(\mathbf{r}_{\rm H_1}^{(1)}-\mathbf{r}_{\rm H_2}^{(1)}\right)\frac{1}{m_{\rm H}}(\mathbf{r}_{\rm O}(0)- \mathbf{r}_{\rm H_2}(0))&\left(\mathbf{r}_{\rm H_1}^{(1)}-\mathbf{r}_{\rm H_2}^{(1)}\right)\frac{2}{m_{\rm H}}(\mathbf{r}_{\rm H_1}(0)- \mathbf{r}_{\rm H_2}(0))
\end{bmatrix}^{-1}\begin{bmatrix}\sigma_1(\mathbf{r}_{\rm O}(\Delta t),\mathbf{r}_{\rm H_1}(\Delta t))\\\sigma_2(\mathbf{r}_{\rm O}(\Delta t),\mathbf{r}_{\rm H_2}(\Delta t))\\\sigma_3(\mathbf{r}_{\rm H_1}(\Delta t),\mathbf{r}_{\rm H_2}(\Delta t))\end{bmatrix}
\end{align*}
$$

参考文献とは$${\tilde{\lambda}_i}$$の定義が係数2の分だけ異なることに注意。

c. bで求めた行列方程式を解いて得られた$${\delta\tilde{\lambda}_i^{\rm(1,solv)}}$$は$${\delta\tilde{\lambda}_i^{\rm(1)}}$$の近似解である。
そこで，

$$
\begin{align*}
\tilde{\lambda}_i&=\tilde{\lambda}_i^{(1)}+\delta \tilde{\lambda}_i^{(1)}\\
&=:\tilde{\lambda}_i^{(1)}+\left\{\delta\tilde{\lambda}_i^{\rm(1,solv)}+\delta \tilde{\lambda}_i^{(2)}\right\}\\
&=\left\{\tilde{\lambda}_i^{(1)}+\delta\tilde{\lambda}_i^{\rm(1,solv)}\right\}+\delta \tilde{\lambda}_i^{(2)}\\
&=:\tilde{\lambda}_i^{(2)}+\delta \tilde{\lambda}_i^{(2)}
\end{align*}
$$

とし，再度$${\delta \tilde{\lambda}_i^{(2)}}$$に関して線形化された行列方程式を解くことにする。
この作業を収束($${\delta \tilde{\lambda}_i^{(n)}\simeq 0}$$)するまで繰り返す。

d. 速度更新に対する未定乗数を$${\mu_i}$$と表記することにする。今，$${t=\Delta t}$$における座標が求まり，式(3.9.16)を用いて$${t=\Delta t/2}$$における速度まで計算できているとする。
このとき，$${t=\Delta t}$$における各速度は以下の式から計算される。

$$
\begin{align*}
\mathbf{v}_{\rm O}(\Delta t)&=\left\{\mathbf{v}_{\rm O}(\Delta t/2)+\frac{\Delta t}{2m_{\rm O}}\mathbf{F}_{\rm O}(\Delta t)\right\}+\frac{\Delta t}{2m_{\rm O}}\left\{2(\mathbf{r}_{\rm O}(\Delta t)-\mathbf{r}_{\rm H_1}(\Delta t))\mu_1+2(\mathbf{r}_{\rm O}(\Delta t)-\mathbf{r}_{\rm H_2}(\Delta t))\mu_2\right\}\\
&=:\mathbf{v}_{\rm O}'+\left(\frac{\mathbf{r}_{\rm O}(\Delta t)-\mathbf{r}_{\rm H_1}(\Delta t)}{m_{\rm O}}\right)\tilde{\mu}_1+\left(\frac{\mathbf{r}_{\rm O}(\Delta t)-\mathbf{r}_{\rm H_2}(\Delta t)}{m_{\rm O}}\right)\tilde{\mu}_2\\
\mathbf{v}_{\rm H_1}(\Delta t)&=\left\{\mathbf{v}_{\rm H_1}(\Delta t/2)+\frac{\Delta t}{2m_{\rm H}}\mathbf{F}_{\rm H_1}(\Delta t)\right\}+\frac{\Delta t}{2m_{\rm H}}\left\{-2(\mathbf{r}_{\rm O}(\Delta t)-\mathbf{r}_{\rm H_1}(\Delta t))\mu_1+2(\mathbf{r}_{\rm H_1}(\Delta t)-\mathbf{r}_{\rm H_2}(\Delta t))\mu_3\right\}\\
&=:\mathbf{v}_{\rm H_1}'-\left(\frac{\mathbf{r}_{\rm O}(\Delta t)-\mathbf{r}_{\rm H_1}(\Delta t)}{m_{\rm H}}\right)\tilde{\mu}_1+\left(\frac{\mathbf{r}_{\rm H_1}(\Delta t)-\mathbf{r}_{\rm H_2}(\Delta t)}{m_{\rm H}}\right)\tilde{\mu}_3\\
\mathbf{v}_{\rm H_2}(\Delta t)&=\left\{\mathbf{v}_{\rm H_2}(\Delta t/2)+\frac{\Delta t}{2m_{\rm H}}\mathbf{F}_{\rm H_2}(\Delta t)\right\}+\frac{\Delta t}{2m_{\rm H}}\left\{-2(\mathbf{r}_{\rm O}(\Delta t)-\mathbf{r}_{\rm H_2}(\Delta t))\mu_2-2(\mathbf{r}_{\rm H_1}(\Delta t)-\mathbf{r}_{\rm H_2}(\Delta t))\mu_3\right\}\\
&=:\mathbf{v}_{\rm H_2}'-\left(\frac{\mathbf{r}_{\rm O}(\Delta t)-\mathbf{r}_{\rm H_2}(\Delta t)}{m_{\rm H}}\right)\tilde{\mu}_2-\left(\frac{\mathbf{r}_{\rm H_1}(\Delta t)-\mathbf{r}_{\rm H_2}(\Delta t)}{m_{\rm H}}\right)\tilde{\mu}_3\\
\end{align*}
$$

式(3.9.18)の拘束条件を具体的に書き下すと以下の通りになる。

$$
\begin{align*}
\left.\frac{\partial \sigma_1}{\partial\mathbf{r}_{\rm O}}\right|_{t=\Delta t}\cdot\mathbf{v}_{\rm O}(\Delta t)+\left.\frac{\partial \sigma_1}{\partial\mathbf{r}_{\rm H_1}}\right|_{t=\Delta t}\cdot\mathbf{v}_{\rm H_1}(\Delta t)&=2\left\{\mathbf{r}_{\rm O}(\Delta t)-\mathbf{r}_{\rm H_1}(\Delta t)\right\}\cdot\left[\left(\mathbf{v}_{\rm O}'-\mathbf{v}_{\rm H_1}'\right)+\left(\frac{1}{m_{\rm O}}+\frac{1}{m_{\rm H}}\right)\left\{\mathbf{r}_{\rm O}(\Delta t)-\mathbf{r}_{\rm H_1}(\Delta t)\right\}\tilde{\mu}_1+\frac{1}{m_{\rm O}}\left\{\mathbf{r}_{\rm O}(\Delta t)-\mathbf{r}_{\rm H_2}(\Delta t)\right\}\tilde{\mu}_2-\frac{1}{m_{\rm H}}\left\{\mathbf{r}_{\rm H_1}(\Delta t)-\mathbf{r}_{\rm H_2}(\Delta t)\right\}\tilde{\mu}_3\right]\\
&=0\\
\left.\frac{\partial \sigma_2}{\partial\mathbf{r}_{\rm O}}\right|_{t=\Delta t}\cdot\mathbf{v}_{\rm O}(\Delta t)+\left.\frac{\partial \sigma_2}{\partial\mathbf{r}_{\rm H_2}}\right|_{t=\Delta t}\cdot\mathbf{v}_{\rm H_2}(\Delta t)&=2\left\{\mathbf{r}_{\rm O}(\Delta t)-\mathbf{r}_{\rm H_2}(\Delta t)\right\}\cdot\left[\left(\mathbf{v}_{\rm O}'-\mathbf{v}_{\rm H_2}'\right)+\frac{1}{m_{\rm O}}\left\{\mathbf{r}_{\rm O}(\Delta t)-\mathbf{r}_{\rm H_1}(\Delta t)\right\}\tilde{\mu}_1+\left(\frac{1}{m_{\rm O}}+\frac{1}{m_{\rm H}}\right)\left\{\mathbf{r}_{\rm O}(\Delta t)-\mathbf{r}_{\rm H_2}(\Delta t)\right\}\tilde{\mu}_2+\frac{1}{m_{\rm H}}\left\{\mathbf{r}_{\rm H_1}(\Delta t)-\mathbf{r}_{\rm H_2}(\Delta t)\right\}\tilde{\mu}_3\right]\\
&=0\\
\left.\frac{\partial \sigma_3}{\partial\mathbf{r}_{\rm H_1}}\right|_{t=\Delta t}\cdot\mathbf{v}_{\rm H_1}(\Delta t)+\left.\frac{\partial \sigma_3}{\partial\mathbf{r}_{\rm H_3}}\right|_{t=\Delta t}\cdot\mathbf{v}_{\rm H_3}(\Delta t)&=2\left\{\mathbf{r}_{\rm H_1}(\Delta t)-\mathbf{r}_{\rm H_2}(\Delta t)\right\}\cdot\left[\left(\mathbf{v}_{\rm H_1}'-\mathbf{v}_{\rm H_2}'\right)-\frac{1}{m_{\rm H}}\left\{\mathbf{r}_{\rm O}(\Delta t)-\mathbf{r}_{\rm H_1}(\Delta t)\right\}\tilde{\mu}_1+\frac{1}{m_{\rm H}}\left\{\mathbf{r}_{\rm O}(\Delta t)-\mathbf{r}_{\rm H_2}(\Delta t)\right\}\tilde{\mu}_2+\frac{2}{m_{\rm H}}\left\{\mathbf{r}_{\rm H_1}(\Delta t)-\mathbf{r}_{\rm H_2}(\Delta t)\right\}\tilde{\mu}_3\right]\\
&=0\\
\end{align*}
$$

$$
\begin{align*}
\begin{bmatrix}\tilde{\mu}_1\\
\tilde{\mu}_2\\
\tilde{\mu}_3
\end{bmatrix}&=-\begin{bmatrix}
\left(\frac{1}{m_{\rm O}}+\frac{1}{m_{\rm H}}\right)\left\{\mathbf{r}_{\rm O}(\Delta t)-\mathbf{r}_{\rm H_1}(\Delta t)\right\}^2 & \frac{1}{m_{\rm O}}\left\{\mathbf{r}_{\rm O}(\Delta t)-\mathbf{r}_{\rm H_1}(\Delta t)\right\}\cdot\left\{\mathbf{r}_{\rm O}(\Delta t)-\mathbf{r}_{\rm H_2}(\Delta t)\right\} &-\frac{1}{m_{\rm H}}\left\{\mathbf{r}_{\rm O}(\Delta t)-\mathbf{r}_{\rm H_1}(\Delta t)\right\}\cdot\left\{\mathbf{r}_{\rm H_1}(\Delta t)-\mathbf{r}_{\rm H_2}(\Delta t)\right\}\\
\frac{1}{m_{\rm O}}\left\{\mathbf{r}_{\rm O}(\Delta t)-\mathbf{r}_{\rm H_2}(\Delta t)\right\}\cdot\left\{\mathbf{r}_{\rm O}(\Delta t)-\mathbf{r}_{\rm H_1}(\Delta t)\right\}&\left(\frac{1}{m_{\rm O}}+\frac{1}{m_{\rm H}}\right)\left\{\mathbf{r}_{\rm O}(\Delta t)-\mathbf{r}_{\rm H_2}(\Delta t)\right\}^2 & \frac{1}{m_{\rm H}}\left\{\mathbf{r}_{\rm O}(\Delta t)-\mathbf{r}_{\rm H_2}(\Delta t)\right\}\cdot\left\{\mathbf{r}_{\rm H_1}(\Delta t)-\mathbf{r}_{\rm H_2}(\Delta t)\right\}\\
-\frac{1}{m_{\rm H}}\left\{\mathbf{r}_{\rm H_1}(\Delta t)-\mathbf{r}_{\rm H_2}(\Delta t)\right\}\cdot\left\{\mathbf{r}_{\rm O}(\Delta t)-\mathbf{r}_{\rm H_1}(\Delta t)\right\}&\frac{1}{m_{\rm H}}\left\{\mathbf{r}_{\rm H_1}(\Delta t)-\mathbf{r}_{\rm H_2}(\Delta t)\right\}\cdot\left\{\mathbf{r}_{\rm O}(\Delta t)-\mathbf{r}_{\rm H_2}(\Delta t)\right\}&\frac{2}{m_{\rm H}}\left\{\mathbf{r}_{\rm H_1}(\Delta t)-\mathbf{r}_{\rm H_2}(\Delta t)\right\}^2
\end{bmatrix}^{-1}
\begin{bmatrix}
\left\{\mathbf{r}_{\rm O}(\Delta t)-\mathbf{r}_{\rm H_1}(\Delta t)\right\}\cdot\left(\mathbf{v}_{\rm O}'-\mathbf{v}_{\rm H_1}'\right)\\
\left\{\mathbf{r}_{\rm O}(\Delta t)-\mathbf{r}_{\rm H_2}(\Delta t)\right\}\cdot\left(\mathbf{v}_{\rm O}'-\mathbf{v}_{\rm H_2}'\right)\\
\left\{\mathbf{r}_{\rm H_1}(\Delta t)-\mathbf{r}_{\rm H_2}(\Delta t)\right\}\cdot\left(\mathbf{v}_{\rm H_1}'-\mathbf{v}_{\rm H_2}'\right)
\end{bmatrix}
\end{align*}
$$

$${\tilde{\mu}_i}$$に関する行列方程式は近似なしで得られたものであり，１回の逆行列計算で解を求めることができるため，反復計算は必要ない。

Problem 3.4

質量$${m}$$，振動数$${\omega}$$を有する一次元調和振動子は以下のハミルトニアンに従う。

$$
\begin{align*}
\mathcal{H}&=\frac{p^2}{2m}+\frac{1}{2}m\omega^2x^2
\end{align*}
$$

位相空間上の関数$${a(x,p)=p^2}$$に対してミクロカノニカルアンサンブル平均$${\langle a\rangle}$$と時間平均

$$
\begin{align*}
\bar{a}&=\frac{1}{T}\int_0^{T}{\rm d}ta(x(t),p(t))
\end{align*}
$$

が等しいことを示せ。ここで，$${T=2\pi/T}$$は運動の１周期である。

初期条件$${x(0),p(0)}$$を用いると解$${x(t),p(t)}$$は以下の通りになる。

$$
\begin{align*}
x(t)&= x(0)\cos\omega t+\frac{p(0)}{m\omega}\sin\omega t\\
p(t)&=-m\omega x(0)\sin\omega t+p(0)\cos\omega t
\end{align*}
$$

$${x(t),p(t)}$$を用いて$${\bar{a}}$$を計算すると，

$$
\begin{align*}
\bar{a}&=\frac{1}{T}\int_0^{T}{\rm d}ta(x(t),p(t))\\
&=\frac{1}{T}\int_0^{T}{\rm d}t\left\{-m\omega x(0)\sin\omega t+p(0)\cos\omega t\right\}^2\\
&=mE
\end{align*}
$$

となる。
一方，$${\langle a\rangle}$$は

$$
\begin{align*}
\langle a\rangle&=\frac{\int_{-\infty}^{\infty}{\rm d}x\int_{-\infty}^{\infty}{\rm d}pp^2\delta(\mathcal{H}-E)}{\int_{-\infty}^{\infty}{\rm d}x\int_{-\infty}^{\infty}{\rm d}p\delta(\mathcal{H}-E)}\\
&=\frac{2m\int_{-\infty}^{\infty}{\rm d}x\int_{-\infty}^{\infty}{\rm d}yy^2\delta(x^2+y^2-E)}{\int_{-\infty}^{\infty}{\rm d}x\int_{-\infty}^{\infty}{\rm d}y\delta(x^2+y^2-E)}\\
&=\frac{m\int_{-\infty}^{\infty}{\rm d}x\int_{-\infty}^{\infty}{\rm d}y(x^2+y^2)\delta(x^2+y^2-E)}{\int_{-\infty}^{\infty}{\rm d}x\int_{-\infty}^{\infty}{\rm d}y\delta(x^2+y^2-E)}\\
&=\frac{m\int_{0}^{\infty}{\rm d}rr^2\delta(r^2-E)}{\int_{0}^{\infty}{\rm d}r\delta(r^2-E)}\\
&=mE
\end{align*}
$$

となる。

$$
\begin{align*}
\therefore \bar{a}&=\langle a\rangle
\end{align*}
$$

Problem 3.5

一次元空間でハミルトニアン$${\mathcal{H}=p^2/2m+U(x)}$$に従う単独粒子の運動を考える。また，以下のように時間発展演算子をトロッター分解することにする：

$$
\begin{align*}
\exp({\rm i}\mathcal{L}\Delta t)&\simeq\exp\left(\frac{\Delta t}{2}\frac{p}{m}\frac{\partial}{\partial x}\right)\exp\left(\Delta tF(x)\frac{\partial}{\partial p}\right)\exp\left(\frac{\Delta t}{2}\frac{p}{m}\frac{\partial}{\partial x}\right)
\end{align*}
$$

a. $${x(\Delta t), p(\Delta t)}$$を決定する有限差分方程式を導出せよ。このアルゴリズムは位置ベルレアルゴリズムとして知られている（$${{\rm Tuckerman}\ et\ al., 1992}$$）。

b. 以下の偏微分行列$${\mathbf{J}}$$（ヤコビ行列）を用いることにより，このアルゴリズムが測度保存かつシンプレックであることを示せ。

c. $${U(x)=-m\omega^2x^2/2}$$の場合における厳密に保存するハミルトニアン（影のハミルトニアン）を求めよ。
ヒント：影のハミルトニアンが以下の数式で表現できることを仮定し，係数$${a,b}$$の値を具体的に決定せよ。

$$
\begin{align*}
\tilde{\mathcal{H}}(x,p;\Delta t)&=a(\Delta t)p^2+b(\Delta t)x^2
\end{align*}
$$

d. このアルゴリズムを実装したプログラムを書き下し，cで求めた影のハミルトニアンが確かに保存すること，及び真のハミルトニアンも十分に小さい時間ステップに対して安定していることを実証せよ。

$$
\begin{align*}
x(\Delta t)&=\exp\left(\frac{\Delta t}{2}\frac{p}{m}\frac{\partial}{\partial x}\right)\exp\left(\Delta tF(x)\frac{\partial}{\partial p}\right)\exp\left(\frac{\Delta t}{2}\frac{p}{m}\frac{\partial}{\partial x}\right)x\\
&=\exp\left(\frac{\Delta t}{2}\frac{p}{m}\frac{\partial}{\partial x}\right)\exp\left(\Delta tF(x)\frac{\partial}{\partial p}\right)\left(x+\frac{\Delta t p}{2m}\right)\\
&=\exp\left(\frac{\Delta t}{2}\frac{p}{m}\frac{\partial}{\partial x}\right)\left(x+\frac{\Delta t p}{2m}+\frac{\Delta t^2 F(x)}{2m}\right)\\
&=x+\frac{\Delta t p}{m}+\frac{\Delta t^2 F\left(x+\frac{\Delta tp}{2m}\right)}{2m}\\
p(\Delta t)&=\exp\left(\frac{\Delta t}{2}\frac{p}{m}\frac{\partial}{\partial x}\right)\exp\left(\Delta tF(x)\frac{\partial}{\partial p}\right)\exp\left(\frac{\Delta t}{2}\frac{p}{m}\frac{\partial}{\partial x}\right)p\\
&=\exp\left(\frac{\Delta t}{2}\frac{p}{m}\frac{\partial}{\partial x}\right)\exp\left(\Delta tF(x)\frac{\partial}{\partial p}\right)p\\
&=\exp\left(\frac{\Delta t}{2}\frac{p}{m}\frac{\partial}{\partial x}\right)\left(p+\Delta tF(x)\right)\\
&=p+\Delta tF\left(x+\frac{\Delta tp}{2m}\right)\\
\end{align*}
$$

$${x\rightarrow x(0), p\rightarrow p(0) }$$と表記を変更すると，

$$
\begin{align*}
x(\Delta t)&=x(0)+\frac{\Delta t p(0)}{m}+\frac{\Delta t^2 F\left(x(0)+\frac{\Delta tp(0)}{2m}\right)}{2m}\\
p(\Delta t)&=p(0)+\Delta tF\left(x(0)+\frac{\Delta tp(0)}{2m}\right)\\
\end{align*}
$$

b. $${\alpha:=x(0)+\frac{\Delta tp(0)}{2m}}$$として$${\mathbf{J}}$$を計算すると，

$$
\begin{align*}
\mathbf{J}&=\begin{pmatrix}\frac{\partial x(\Delta t)}{\partial x(0)} & \frac{\partial x(\Delta t)}{\partial p(0)}\\
\frac{\partial p(\Delta t)}{\partial x(0)} & \frac{\partial p(\Delta t)}{\partial p(0)}\end{pmatrix}\\
&=\begin{pmatrix}1+\frac{\Delta t^2}{2m}\frac{\partial F}{\partial \alpha} & \frac{\Delta t}{m}+\frac{\Delta t^3}{4m^2}\frac{\partial F}{\partial \alpha}\\
\Delta t\frac{\partial F}{\partial \alpha} & 1+\frac{\Delta t^2}{2m}\frac{\partial F}{\partial \alpha}\end{pmatrix}\\
\end{align*}
$$

より，

$$
\begin{align*}
|\mathbf{J}|&=1\\
\mathbf{J}^{\rm T}\mathbf{M}\mathbf{J}&=
\begin{pmatrix}1+\frac{\Delta t^2}{2m}\frac{\partial F}{\partial \alpha} & \Delta t\frac{\partial F}{\partial \alpha}\\
\frac{\Delta t}{m}+\frac{\Delta t^3}{4m^2}\frac{\partial F}{\partial \alpha}& 1+\frac{\Delta t^2}{2m}\frac{\partial F}{\partial \alpha}\end{pmatrix}
\begin{pmatrix}0&1\\-1&0\end{pmatrix}
\begin{pmatrix}1+\frac{\Delta t^2}{2m}\frac{\partial F}{\partial \alpha} & \frac{\Delta t}{m}+\frac{\Delta t^3}{4m^2}\frac{\partial F}{\partial \alpha}\\
\Delta t\frac{\partial F}{\partial \alpha} & 1+\frac{\Delta t^2}{2m}\frac{\partial F}{\partial \alpha}\end{pmatrix}\\
&=
\begin{pmatrix}1+\frac{\Delta t^2}{2m}\frac{\partial F}{\partial \alpha} & \Delta t\frac{\partial F}{\partial \alpha}\\
\frac{\Delta t}{m}+\frac{\Delta t^3}{4m^2}\frac{\partial F}{\partial \alpha}& 1+\frac{\Delta t^2}{2m}\frac{\partial F}{\partial \alpha}\end{pmatrix}
\begin{pmatrix}\Delta t\frac{\partial F}{\partial \alpha} & 1+\frac{\Delta t^2}{2m}\frac{\partial F}{\partial \alpha}\\
-1-\frac{\Delta t^2}{2m}\frac{\partial F}{\partial \alpha} & -\frac{\Delta t}{m}-\frac{\Delta t^3}{4m^2}\frac{\partial F}{\partial \alpha}\end{pmatrix}\\
&=\begin{pmatrix}0&1\\-1&0\end{pmatrix}
\end{align*}
$$

より，このアルゴリズムは測度保存かつシンプレックである。

c. $${U(x)=-\frac{m\omega^2}{2}x^2}$$のとき，$${F(x)=m\omega^2x}$$となるため，時間発展は以下の方程式に従う。

$$
\begin{align*}
x(\Delta t)&=\left\{1+\frac{(\omega\Delta t)^2}{2}\right\}x(0)+\left\{1+\frac{(\omega\Delta t)^2}{4}\right\}\frac{\Delta tp(0)}{m}\\
p(\Delta t)&=\Delta m\omega^2x(0)+\left\{1+\frac{(\omega\Delta t)^2}{2}\right\}p(0)\\
\end{align*}
$$

ここで，

$$
\begin{align*}
\tilde{\mathcal{H}}(x,p;\Delta t)&=a(\Delta t)p(\Delta t)^2+b(\Delta t)x(\Delta t)^2\\
&=a(0)p(0)^2+b(0)x(0)^2
\end{align*}
$$

を満たす影のハミルトニアンが存在すると仮定する。
$${p(\Delta t)x(\Delta t)}$$の項が0となるためには，

$$
\begin{align*}
a(\Delta t)&=-\frac{1}{(m\omega)^2}\left\{1+\frac{(\omega\Delta t)^2}{4}\right\}b(\Delta t)
\end{align*}
$$

となる必要がある。
この条件を用いて，$${a(\Delta t),\ b(\Delta t)}$$を$${b(0)}$$で表すと，

$$
\begin{align*}
b(\Delta t)&=b(0)\\
a(\Delta t)&=-\frac{1}{(m\omega)^2}\left\{1+\frac{(\omega\Delta t)^2}{4}\right\}b(0)
\end{align*}
$$

となる。$${b(0)=-2m\omega^2}$$に選ぶと，

$$
\begin{align*}
\tilde{\mathcal{H}}(x,p;\Delta t)&=\left\{1+\frac{(\omega\Delta t)^2}{4}\right\}\frac{p(\Delta t)^2}{2m}-\frac{m\omega^2}{2}x(\Delta t)^2\\
\end{align*}
$$

d. pythonによるプログラム例を以下に示す。

# import modules
import numpy as np

# Input parameters
x       = 1
p       = 1
dt      = 0.0001
weight  = 1
omega   = 5
n_steps = 5000

# Define functions
def force(x):
    return weight * (omega ** 2) * x
def shadow_H(x,p):
    return 0.5 * (1 + 0.25 * (omega * dt) ** 2 ) * p ** 2 / weight - 0.5 * weight * ( omega * x) ** 2 
def true_H(x,p):
    return 0.5 * p ** 2 / weight - 0.5 * weight * ( omega * x) ** 2

#----- below is the code -----#
results = []
for i in range(n_steps):
    if i % (n_steps // 100) == 0:
        results.append([i, shadow_H(x,p), true_H(x,p)])
  
    # Update coordinate and momentum
    x += 0.5 * dt * p / weight
    p += dt * force(x)
    x += 0.5 * dt * p / weight
    print(x,p)
results.append([i, shadow_H(x,p), true_H(x,p)])

# Export the result to a csv file
header = 'n_step, shadow_h, true_h'
np.savetxt('results.csv', np.array(results), header = header, delimiter=",", comments = '')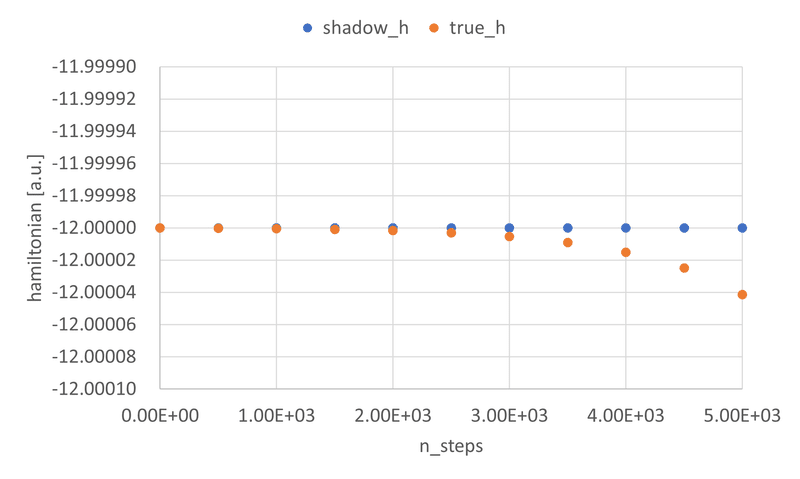

Problem 3.6

以下のポテンシャル下で運動する一次元の単粒子を考える。

$$
\begin{align*}
U(x)&=\frac{1}{2}m(\omega^2+\Omega^2)x^2
\end{align*}
$$

ここで，$${\Omega\ll\omega}$$である。このポテンシャルによる力には２つの時間スケールがあり，それらをそれぞれ$${F_{\rm fast}=-m\omega^2 x,\ F_{\rm slow}=-m\Omega^2 x}$$とする。式(3.11.6)の時間発展演算子の分解形式を用いて，この系を時間ステップ$${\Delta t}$$だけ積分することを考える，ここで$${{\rm i}\mathcal{L}_{\rm fast}}$$は早い振動子に対する完全なリウヴィル演算子である。

$$
\begin{align*}
&\ \exp\left({\rm i}\mathcal{L}\Delta t\right)\\
&=\exp\left({\rm i}\mathcal{L}_{\rm slow}\frac{\Delta t}{2}\right)\exp\left({\rm i}\mathcal{L}_{\rm fast}\Delta t\right)\exp\left({\rm i}\mathcal{L}_{\rm slow}\frac{\Delta t}{2}\right)
\end{align*}\tag{3.11.6}
$$

a. 位相空間のベクトル$${(x,p)}$$への演算子$${\exp\left({\rm i}\mathcal{L}_{\rm fast}\Delta t\right)}$$の作用は式(3.11.8)にあるように解析的に評価できる。

$$
\begin{align*}
p&=p+0.5*{\rm d}t*F_{\rm slow}\\
x_{\rm temp}&=x*\cos({\rm arg})+p/(m*\omega)*\sin({\rm arg})\\
p_{\rm temp}&=p*\cos({\rm arg})-m*\omega*x*\sin({\rm arg})\\
x&=x_{\rm temp}\\
p&=p_{\rm temp}\\
p&=p+0.5*{\rm d}t*F_{\rm slow}\\
\end{align*}\tag{3.11.8}
$$

ここで，$${{\rm arg}=\omega*{\rm d}t}$$である。
この事実を用いて，位相空間での時間発展が以下の数式で表せられることを示せ。

$$
\begin{align*}
\begin{pmatrix}x(\Delta t)\\ p(\Delta t)\end{pmatrix}&=\mathbf{A}(\omega,\Omega,\Delta t)\begin{pmatrix}x(0)\\ p(0)\end{pmatrix}
\end{align*}
$$

ここで，$${\mathbf{A}(\omega,\Omega,\Delta t)}$$は2×2の行列である。この行列の具体的な表式を導け。

b. $${{\rm det}(\mathbf{A})=1}$$を示せ。

c. $${\mathbf{A}}$$の固有値が$${\Delta t}$$の大きさに依存して，$${-2 < {\rm Tr}(\mathbf{A})<2}$$を満たす場合は共役な複素数のペア，もしくは$${|{\rm Tr}(\mathbf{A})|\geq 2}$$を満たす場合は両方とも実数となることを示せ。

d. $${\Delta t=\pi/\omega}$$に選んだ際の数値的な意味合いを論ぜよ。

a. $${F_{\rm slow}(x)=-m\Omega^2 x}$$を式(3.11.7)に代入すると，

$$
\begin{align*}
x(\Delta t)&=x(0)\cos\omega\Delta t+\frac{1}{\omega}\left[\frac{p(0)}{m}-\frac{\Delta t}{2}\Omega^2x(0)\right]\sin\omega\Delta t\\
&=\left(\cos\omega\Delta t-\frac{\Omega^2\Delta t}{2\omega}\sin\omega\Delta t\right)x(0)+\frac{\sin\omega\Delta t}{m\omega}p(0)\\
p(\Delta t)&=\left[p(0)-\frac{\Delta t m\Omega^2}{2}x(0)\right]\cos\omega\Delta t-m\omega x(0)\sin\omega\Delta t-\frac{\Delta tm\Omega^2}{2}\left[\left(\cos\omega\Delta t-\frac{\Omega^2\Delta t}{2\omega}\sin\omega\Delta t\right)x(0)+\frac{\sin\omega\Delta t}{m\omega}p(0)\right]\\
&=-m\left[\Omega^2\Delta t\cos\omega\Delta t+\left\{\omega-\frac{\Omega^4\Delta t^2}{4\omega}\right\}\sin\omega\Delta t\right]x(0)+\left(\cos\omega\Delta t-\frac{\Omega^2\Delta t}{2\omega}\sin\omega\Delta t\right)p(0)
\end{align*}
$$

$$
\begin{align*}
\therefore \mathbf{A}(\omega,\Omega,\Delta t)&=\begin{pmatrix}
\left(\cos\omega\Delta t-\frac{\Omega^2\Delta t}{2\omega}\sin\omega\Delta t\right)&
\frac{\sin\omega\Delta t}{m\omega}\\
-m\left[\Omega^2\Delta t\cos\omega\Delta t+\left\{\omega-\frac{\Omega^4\Delta t^2}{4\omega}\right\}\sin\omega\Delta t\right]&
\left(\cos\omega\Delta t-\frac{\Omega^2\Delta t}{2\omega}\sin\omega\Delta t\right)
\end{pmatrix}
\end{align*}
$$

$$
\begin{align*}
{\rm det}(\mathbf{A})&=\left(\cos\omega\Delta t-\frac{\Omega^2\Delta t}{2\omega}\sin\omega\Delta t\right)^2+ \frac{\sin\omega\Delta t}{\omega}\left[\Omega^2\Delta t\cos\omega\Delta t+\left\{\omega-\frac{\Omega^4\Delta t^2}{4\omega}\right\}\sin\omega\Delta t\right]\\
&=\cos\omega^2\Delta t+\sin\omega^2\Delta t\\
&=1\\
\therefore {\rm det}(\mathbf{A})&=1
\end{align*}
$$

c. $${f(\omega,\Omega,\Delta t):=\cos\omega\Delta t-\frac{\Omega^2\Delta t}{2\omega}\sin\omega\Delta t}$$，及び$${\mathbf{A}(\omega,\Omega,\Delta t)}$$の固有値を$${\lambda}$$とすると，

$$
\begin{align*}
{\rm det}(\mathbf{A}-\lambda\mathbf{I})&=1-2f(\omega,\Omega,\Delta t)\lambda+\lambda^2\\
&=0\\
\therefore \lambda &=f(\omega,\Omega,\Delta t)\pm\sqrt{f(\omega,\Omega,\Delta t)^2-1}
\end{align*}
$$

また，$${{\rm Tr}(\mathbf{A})=2f(\omega,\Omega,\Delta t)}$$であることを考慮すると，題意は示されたことになる。

d. $${\Delta t=\pi/\omega}$$の場合，$${x(t+\Delta t)=-x(t)}$$となり，$${F_{\rm slow}}$$による影響が見えなくなってしまう。

Problem 3.7

以下のポテンシャル下で運動する一次元の単粒子を考える。

$$
\begin{align*}
U(x)&=\frac{1}{2}m\omega^2x^2+\frac{g}{4}x^4
\end{align*}
$$

$${m=1,\ \omega=1,\ g=0.1,\ x(0)=0,\ p(0)=1}$$に選んだ際のこの問題に対するRESPAアルゴリズムを実装したプログラムを書け。$${\delta t=0.01}$$に選んだ場合，$${\Delta t}$$をどの程度大きくできるだろうか？RESPAによる軌跡を単一の小さい時間ステップの場合の軌跡と比較せよ。プログラムを用いてRESPAがおおよそ$${\Delta t}$$の2次のオーダーの精度であることを実証せよ。

$${F_{\rm fast}(x):=-m\omega^2x,\ F_{\rm slow}(x):=-gx^3}$$とする。
pythonによるプログラム例を以下に示す。

# import modules
import numpy as np

# Input parameters
m       = 1
omega    = 1
x        = 0
p        = 1
g        = 0.1
dt       = 0.01
n        = 1000
Dt       = n * dt
n_steps  = 500000

# Define functions
def force_fast(x):
    return - m * (omega ** 2) * x
def force_slow(x):
    return - g * (x ** 3)
def IntegrateRESPA(x, p):
    p += 0.5 * Dt * force_slow(x)
    for _ in range(n):
        p += 0.5 * dt * force_fast(x)
        x += dt * p / m
        p += 0.5 * dt * force_fast(x)
    p += 0.5 * Dt * force_slow(x)
    return x, p
def Integrate(x, p):
    p += 0.5 * dt * (force_fast(x) + force_slow(x))
    x += dt * p / m
    p += 0.5 * dt * (force_fast(x) + force_slow(x))
    return x, p

#----- below is the code -----#
traj_single = [[x,p]]
traj_respa = [[x,p]]
traj_error = [[0,0]]
x_single, p_single = x, p
x_respa, p_respa = x, p
for i in range(n_steps):
    x_single, p_single = Integrate(x_single, p_single)
    
    if i % n == 0:
        x_respa, p_respa = IntegrateRESPA(x_respa, p_respa)
        traj_single.append([x_single, p_single])
        traj_respa.append([x_respa, p_respa])
        if i != 0:
            x_error = abs((x_single - x_respa) / x_single)
            p_error = abs((p_single - p_respa) / p_single)
            traj_error.append([x_error, p_error])
            print(x_error, p_error)

# Export the result to csv file
header = 'x, p'
np.savetxt('result_single.csv', traj_single, header = header, delimiter=",", comments = '')
np.savetxt('result_respa.csv', traj_respa, header = header, delimiter=",", comments = '')
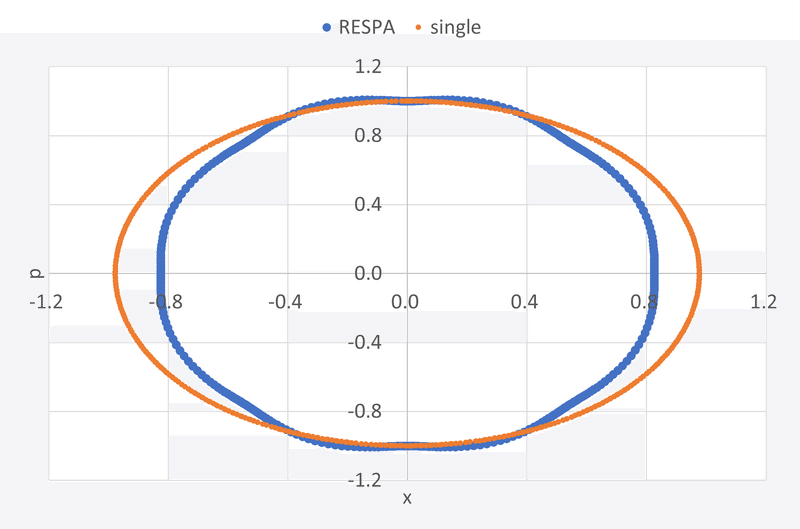
print(np.mean(traj_error))

$${n=\Delta t/\delta t=1000}$$の場合の位相空間上の軌跡を以下に示す。

Problem 3.8

式(3.11.12)のアルゴリズムの疑似コードを生成せよ。

$$
\begin{align*}
\exp\left({\rm i}\mathcal{L}\Delta T\right)&\ \\
&=\exp\left(\frac{\Delta T}{2}F_{\rm slow}\frac{\partial}{\partial p}\right)\\
&\ \ \ \times\left\{\exp\left(\frac{\Delta t}{2}F_{\rm intermed}\frac{\partial}{\partial p}\right)\right.\\
&\ \ \ \left[\exp\left(\frac{\delta t}{2}F_{\rm fast}\frac{\partial}{\partial p}\right)\exp\left(\frac{\delta t}{2}F_{\rm fast}\frac{\partial}{\partial p}\right)\exp\left(\frac{\delta t}{2}F_{\rm fast}\frac{\partial}{\partial p}\right)\right]^n\\
&\ \ \ \ \left.\exp\left(\frac{\Delta t}{2}F_{\rm intermed}\frac{\partial}{\partial p}\right)\right\}^m\exp\left(\frac{\Delta T}{2}F_{\rm slow}\frac{\partial}{\partial p}\right)
\end{align*}\tag{3.11.12}
$$

参考文献の表記に倣うと疑似コードは以下のようになる。

p = p + 0.5 * ΔT * F_slow
for i = 1 to m
  p = p + 0.5 * Δt * F_intermed
  for j = 1 to n
    p = p + 0.5 * δt * F_fast
    x = x + δt * p/m
    # Recalculate fast force
    p = p + 0.5 * δt * F_fast
  endfor
  # Recalculate intermediate force
  p = p + 0.5 * Δt * F_intermed
endfor
# Recalculate slow force
p = p + 0.5 * ΔT * F_slow.

Problem 3.9

ミクロカノニカルアンサンブルにおける体積$${V}$$を圧力$${P}$$にルジャンドル変換した場合のエネルギーを求めよ。何の熱力学関数がエネルギーを代表する量となるか？

NVSアンサンブルにおいて，体積$${V}$$を圧力$${P}$$にルジャンドル変換したエネルギーを$${H(N,P,E)}$$とおくと，

$$
\begin{align*}
H(N,P,E)&=E(N,V(P),S)-\left(\frac{\partial E}{\partial V}\right)_{N,S}V(P)\\
&=E(N,V(P),S)+PV(P)
\end{align*}
$$

が得られる。$${H(N,P,E)}$$はエンタルピーと称されるNPEアンサンブルにおける完全な熱力学関数であり，NPEアンサンブルにおける代表的なエネルギー量と解釈される。

参考文献

Mark Tuckerman, Statistical Mechanics: Theory and Molecular Simulation (Oxford Graduate Texts)

この記事が気に入ったらサポートをしてみませんか？