Statistical Mechanics: Theory and Molecular SimulationはMark Tuckermanによって著された分子シミュレーションに関連した熱・統計物理学，及び量子力学の参考書になります。

現時点では（恐らく）和訳がないこともあり，日本での知名度はあまりないような気がしますが，被引用数が1500を超えていることを考えると海外では高く認知されている参考書みたいです。

https://scholar.google.com/citations?user=w_7furwAAAAJ

本記事では，Chapter 13（Classical time-dependent statistical mechanics）の章末問題の和訳とその解答例を紹介します。解答例に間違いが見受けられた場合はお知らせいただけると助かります。

Problem 13.1

２つの速度自己相関関数のモデルを考える。

$$
\begin{align*}
C_1(t)&=\left\langle v^2\right\rangle{\rm e}^{-\gamma t}\\
C_2(t)&=\left\langle v^2\right\rangle{\rm e}^{-\gamma t}\cos(\alpha t)\\
\end{align*}
$$

a. それぞれのモデルに対して拡散係数$${D_1,\ D_2}$$を計算せよ。大小関係はどうなるか？

b. 2つの拡散係数を比較し，それぞれどのような物理的状況を描写したものなのか述べよ。

a. 

$$
\begin{align*}
D_1&=\int_0^{\infty}{\rm d}tC_1(t)\\
&=\left\langle v^2\right\rangle\int_0^{\infty}{\rm e}^{-\gamma t}\\
&=\frac{\left\langle v^2\right\rangle}{\gamma}\\
D_2&=\int_0^{\infty}{\rm d}tC_2(t)\\
&=\left\langle v^2\right\rangle\int_0^{\infty}{\rm e}^{-\gamma t}\cos(\alpha t)\\
&=\left\langle v^2\right\rangle\Re\left[\int_0^{\infty}{\rm e}^{-(\gamma-{\rm i}\alpha) t}\right]\\
&=\frac{\left\langle v^2\right\rangle}{\gamma}\left(\frac{1}{1+(\alpha/\gamma)^2}\right)\\
\end{align*}\tag{1.1}
$$

$$
\begin{align*}
\therefore D_1 &> D_2
\end{align*}\tag{1.2}
$$

b. モデル1は自己相関が単純に指数関数的に減衰するため，ランダムな運動しか存在しない。一方，モデル2には周期運動も混在する。

Problem 13.2

古典的な等方的等温等圧（NPT）アンサンブルは，Green-Kubo理論を介して物質の体積粘性係数を決定するために特に有用である。

a. 線形応答の表式は初期分布を$${f_0(\mathcal{H}(\mathbf{r},\mathbf{p}),V)=\exp(-\beta(\mathcal{H}(\mathbf{r},\mathbf{p})+PV))/\Delta(N,P,T)}$$（等温等圧分布関数）に選んでも不変であることを示せ。

b. 次に，外部の圧縮場と相互作用する系を考え，以下の運動方程式に従うとする。

$$
\begin{align*}
\dot{r}_{i,\alpha}&=\frac{p_{i,\alpha}}{m_i}+\sum_{\beta}r_{i,\beta}M_{\beta\alpha}\\
\dot{p}_{i,\alpha}&=F_{i,\alpha}-\sum_{\beta}p_{i,\beta}M_{\beta\alpha}\\
\end{align*}
$$

ここで，$${\alpha,\ \beta}$$は３つの空間次元$${x,y,z}$$のインデックスである。運動方程式が非圧縮条件を満たすことを示せ。

c. $${M_{\alpha\beta}}$$を

$$
\begin{align*}
M_{\alpha\beta}&=\frac{1}{3}\gamma\delta_{\alpha\beta}
\end{align*}
$$

に選んだ場合を考える。ここで，$${\gamma}$$は圧縮率である。
体積粘性係数$${\eta_{\rm V}}$$は一般化されたニュートンの粘性法則によって与えられる。

$$
\begin{align*}
\langle V\rangle_{\rm eq}\eta_{\rm V}&=-\lim_{t\rightarrow \infty}\frac{\langle P(t)V(t)\rangle}{\gamma}
\end{align*}
$$

ここで，$${\langle\cdots\rangle_{\rm eq}}$$は（平衡）等方的NPT分布関数の平均，$${\langle\cdots\rangle}$$は非平衡平均を表す。線形応答理論を用いて$${\langle P(t)V(t)\rangle}$$を評価し，$${\eta_{\rm V}}$$の適切なGreen-Kubo表式を導出せよ。

a.

$$
\begin{align*}
\int{\rm d}\mathbf{x}f_0(\mathcal{H}(\mathbf{x}))&\rightarrow\int_0^{\infty}{\rm d}V\int_{D(V)}{\rm d}\mathbf{x}f_0(\mathcal{H}(\mathbf{x}), V)
\end{align*}
$$

とすれば，導出については同じ理屈が通用する。

b. 

$$
\begin{align*}
\mathbf{M}&:=\begin{bmatrix}
M_{xx} & M_{xy} & M_{xz}\\
M_{yx} & M_{yy} & M_{yz}\\
M_{zx} & M_{zy} & M_{zz}
\end{bmatrix}
\end{align*}\tag{2.1}
$$

と定義し，運動方程式を

$$
\begin{align*}
\dot{\mathbf{r}}_{i}&=\frac{\mathbf{p}_{i}}{m_i}+\mathbf{M}^{\rm T}\mathbf{r}_{i}\\
\dot{\mathbf{p}}_{i}&=\mathbf{F}_{i}-\mathbf{M}^{\rm T}\mathbf{p}_{i}\\
\end{align*}\tag{2.2}
$$

と表記することにする。

$$
\begin{align*}
\nabla_{\mathbf{x}}\cdot\dot{\mathbf{x}}&=\sum_{i=1}^N\left[\frac{\partial \dot{\mathbf{r}}_i}{\partial \mathbf{r}_i}+\frac{\partial \dot{\mathbf{p}}_i}{\partial \mathbf{p}_i}\right]\\
&=\sum_{i=1}^N\left[\frac{\partial \mathbf{M}^{\rm T}\mathbf{r}_{i}}{\partial \mathbf{r}_i}-\frac{\partial \mathbf{M}^{\rm T}\mathbf{p}_{i}}{\partial \mathbf{p}_i}\right]\\
&=N\left({\rm Tr}[\mathbf{M}]-{\rm Tr}[\mathbf{M}]\right)\\
&=0
\end{align*}\tag{2.3}
$$

c. 

$$
\begin{align*}
j(\mathbf{x})&=-\sum_{i=1}^N\left\{\mathbf{D}_i^{\rm T}\frac{\partial\mathcal{H}}{\partial\mathbf{p}_i}+\mathbf{C}_i^{\rm T}\frac{\partial\mathcal{H}}{\partial\mathbf{q}_i}\right\}\\
&=-\sum_{i=1}^N\left\{\left(-\mathbf{M}^{\rm T}\mathbf{p}_i\right)^{\rm T}\left(\frac{\mathbf{p}_i}{m_i}\right)+\left(-\mathbf{M}^{\rm T}\mathbf{r}_i\right)^{\rm T}\left(-\mathbf{F}_i\right)\right\}\\
&=\sum_{i=1}^N\left\{\frac{\mathbf{p}_i^{\rm T}\mathbf{M}\mathbf{p}_i}{m_i}+\mathbf{r}_i^{\rm T}\mathbf{M}\mathbf{F}_i\right\}\\
&=\frac{\gamma}{3}\sum_{i=1}^N\left\{\frac{\mathbf{p}_i^{\rm T}\mathbf{p}_i}{m_i}+\mathbf{r}_i^{\rm T}\mathbf{F}_i\right\}\\
&=\gamma V\mathcal{P}(\mathbf{x})
\end{align*}\tag{2.4}
$$

より，

$$
\begin{align*}
&\langle P(t)V(t)\rangle\\
&=P\langle V\rangle_{\rm eq}-\beta\int_{0}^{t}{\rm d}s\int_{0}^{\infty}{\rm d}V\int_{D(V)}{\rm d}\mathbf{x}f_0(\mathcal{H},V)\mathcal{P}(\mathbf{x}_{t-s}(\mathbf{x}))Vj(\mathbf{x})\\
&=P\langle V\rangle_{\rm eq}-\beta\gamma\int_{0}^{t}{\rm d}s\int_{0}^{\infty}{\rm d}V\int_{D(V)}{\rm d}\mathbf{x}f_0(\mathcal{H},V)\mathcal{P}(\mathbf{x}_{t-s}(\mathbf{x}))\mathcal{P}(\mathbf{x})\\
&=P\langle V\rangle_{\rm eq}-\beta\gamma\int_{0}^{t}{\rm d}\tau\left\langle\mathcal{P}(0)\mathcal{P}(\tau)\right\rangle\\
\end{align*}\tag{2.5}
$$

$$
\begin{align*}
\therefore \eta_{\rm V}&=-\lim_{t\rightarrow \infty}\frac{\langle P(t)V(t)\rangle}{\gamma \langle V\rangle_{\rm eq}}\\
&=-\frac{P}{\gamma}+\frac{\beta}{\langle V\rangle_{\rm eq}}\int_{0}^{\infty}{\rm d}t\left\langle\mathcal{P}(0)\mathcal{P}(t)\right\rangle
\end{align*}\tag{2.6}
$$

Problem 13.3

(13.3.34)式のEinsteinの関係式が(13.3.33)式のGreen–Kuboの関係式から導出できることを示せ。

$$
\begin{align*}
D&=\frac{1}{3}\int_0^{\infty}{\rm d}t\frac{1}{N}\sum_{i=1}^N\left\langle\dot{\mathbf{r}}_i(0)\cdot\dot{\mathbf{r}}_i(t)\right\rangle
\end{align*}\tag{13.3.33}
$$

$$
\begin{align*}
D&=\frac{1}{6}\lim_{t\rightarrow\infty}\frac{{\rm d}}{{\rm d}t}\frac{1}{N}\sum_{i=1}^N\left\langle\left|\mathbf{r}_i(t)-\mathbf{r}_i(0)\right|^2\right\rangle
\end{align*}\tag{13.3.34}
$$

長時間極限（$${t\gg 1}$$）において，平均二乗変位が$${t}$$に線形に比例することを考慮すると，

$$
\begin{align*}
\int_0^{\infty}{\rm d}t\left\langle\dot{\mathbf{r}}(0)\cdot\dot{\mathbf{r}}(t)\right\rangle&=\frac{1}{2}\lim_{t\rightarrow\infty}\frac{{\rm d}}{{\rm d}t}\left\langle\left|\mathbf{r}(t)-\mathbf{r}(0)\right|^2\right\rangle\\
&=\frac{1}{2}\lim_{t\rightarrow\infty}\frac{\left\langle\left|\mathbf{r}(t)-\mathbf{r}(0)\right|^2\right\rangle}{t}
\end{align*}\tag{3.1}
$$

が示されれば良いことになる。

$$
\begin{align*}
\mathbf{r}(t)-\mathbf{r}(0)&=\int_{0}^t{\rm d}t'\dot{\mathbf{r}}(t')
\end{align*}\tag{3.2}
$$

より，

$$
\begin{align*}
\left\langle\left|\mathbf{r}(t)-\mathbf{r}(0)\right|^2\right\rangle&=\int_{0}^t{\rm d}t'\int_{0}^t{\rm d}t''\left\langle\left|\dot{\mathbf{r}}(t')\cdot\dot{\mathbf{r}}(t'')\right|\right\rangle\\
&=2\int_{0}^t{\rm d}t'\int_{0}^{t'}{\rm d}t''\left\langle\left|\dot{\mathbf{r}}(t')\cdot\dot{\mathbf{r}}(t'')\right|\right\rangle\\
&=2\int_{0}^t{\rm d}t'\int_{0}^{t'}{\rm d}\tau\left\langle\left|\dot{\mathbf{r}}(t')\cdot\dot{\mathbf{r}}(t'-\tau)\right|\right\rangle\\
&=\frac{1}{2}\int_{0}^t{\rm d}t'\int_{0}^{t'}{\rm d}\tau\left\langle\left|\dot{\mathbf{r}}(\tau)\cdot\dot{\mathbf{r}}(0)\right|\right\rangle\\
&=2\left\{\left[t'\int_{0}^{t'}{\rm d}\tau\left\langle\left|\dot{\mathbf{r}}(\tau)\cdot\dot{\mathbf{r}}(0)\right|\right\rangle\right]_0^{t}-\int_{0}^t{\rm d}t't'\left\langle\left|\dot{\mathbf{r}}(t')\cdot\dot{\mathbf{r}}(0)\right|\right\rangle\right\}\\
&=2\left\{t\int_{0}^{t}{\rm d}\tau\left\langle\left|\dot{\mathbf{r}}(\tau)\cdot\dot{\mathbf{r}}(0)\right|\right\rangle-\int_{0}^t{\rm d}t't'\left\langle\left|\dot{\mathbf{r}}(t')\cdot\dot{\mathbf{r}}(0)\right|\right\rangle\right\}\\
&=2t\int_{0}^{t}{\rm d}t'\left(1-\frac{t'}{t}\right)\left\langle\left|\dot{\mathbf{r}}(\tau)\cdot\dot{\mathbf{r}}(0)\right|\right\rangle
\end{align*}\tag{3.3}
$$

$$
\begin{align*}
\therefore \frac{1}{2}\lim_{t\rightarrow\infty}\frac{\left\langle\left|\mathbf{r}(t)-\mathbf{r}(0)\right|^2\right\rangle}{t}&=\lim_{t\rightarrow\infty}\int_{0}^{t}{\rm d}t'\left(1-\frac{t'}{t}\right)\left\langle\left|\dot{\mathbf{r}}(\tau)\cdot\dot{\mathbf{r}}(0)\right|\right\rangle\\
&=\int_{0}^{\infty}{\rm d}t'\left\langle\left|\dot{\mathbf{r}}(\tau)\cdot\dot{\mathbf{r}}(0)\right|\right\rangle
\end{align*}\tag{3.4}
$$

Problem 13.4

時間依存の境界条件がない場合において，(13.5.22)式によって(13.5.23)式が保存することを証明せよ。

$$
\begin{align*}
\dot{\mathbf{r}}_i&=\frac{\mathbf{p}_i}{m_i}+\mathbf{r}_i\cdot\nabla\mathbf{u}\\
\dot{\mathbf{p}}_i&=\mathbf{F}_i-\mathbf{p}_i\cdot\nabla\mathbf{u}-m_i\mathbf{r}_i\cdot\nabla\mathbf{u}\cdot\nabla\mathbf{u}-\frac{p_{\eta_1}}{Q_1}\mathbf{p}_i\\
\dot{\zeta}&=\sum_{i=1}^N\mathbf{r}_i\cdot\nabla\mathbf{u}\cdot\mathbf{p}_i\frac{p_{\eta_1}}{Q_1}\\
\dot{\eta}_j&=\frac{p_{\eta_j}}{Q_j}\ \ \ \ \ j=1,\cdots,M\\
\dot{p}_{\eta_1}&=\left[\sum_{i=1}^N\frac{\mathbf{p}_i^2}{m_i}-3Nk_{\rm B}T\right]-\frac{p_{\eta_2}}{Q_2}p_{\eta_1}\\
\dot{p}_{\eta_j}&=\left[\frac{p_{\eta_{j-1}}^2}{Q_{j-1}}-k_{\rm B}T\right]-\frac{p_{\eta_{j+1}}}{Q_{j+1}}p_{\eta_j}\ \ \ \ \ j=2,\cdots,M-1\\
\dot{p}_{\eta_M}&=\left[\frac{p_{\eta_{M-1}}^2}{Q_{M-1}}-k_{\rm B}T\right]
\end{align*}\tag{13.5.22}
$$

$$
\begin{align*}
\mathcal{H}'&=\sum_{i=1}^N\frac{\left(\mathbf{p}_i+m_i\mathbf{r}_i\cdot\nabla\mathbf{u}\right)^2}{2m_i}+U(\mathbf{r})+\sum_{j=1}^M\frac{p_{\eta_j}^2}{2Q_j}\\
&\ \ \ \ \ +3Nk_{\rm B}T\eta_1+k_{\rm B}T\sum_{j=2}^M\eta_j+\zeta
\end{align*}\tag{13.5.23}
$$

$$
\begin{align*}
\frac{\rm d}{{\rm d}t}\frac{\left(\mathbf{p}_i+m_i\mathbf{r}_i\cdot\nabla\mathbf{u}\right)^2}{2m_i}&=\frac{\left(\dot{\mathbf{p}}_i+m_i\dot{\mathbf{r}}_i\cdot\nabla\mathbf{u}\right)\cdot\left(\mathbf{p}_i+m_i\mathbf{r}_i\cdot\nabla\mathbf{u}\right)}{m_i}\\
&=\left(\mathbf{F}_i-\frac{p_{\eta_1}}{Q_1}\mathbf{p}_i\right)\cdot\left(\frac{\mathbf{p}_i}{m_i}+\mathbf{r}_i\cdot\nabla\mathbf{u}\right)\\
\end{align*}\tag{4.1}
$$

$$
\begin{align*}
\frac{\rm d}{{\rm d}t}U(\mathbf{r})&=\sum_{i=1}^N\frac{\partial U}{\partial\mathbf{r}_i}\cdot\dot{\mathbf{r}}_i\\
&=-\sum_{i=1}^N\mathbf{F}_i\cdot\left(\frac{\mathbf{p}_i}{m_i}+\mathbf{r}_i\cdot\nabla\mathbf{u}\right)\\
\end{align*}\tag{4.2}
$$

$$
\begin{align*}
\frac{\rm d}{{\rm d}t}\sum_{j=1}^M\frac{p_{\eta_j}^2}{2Q_j}&=\frac{\dot{p}_{\eta_1}p_{\eta_1}}{Q_1}+\sum_{j=2}^{M-1}\frac{\dot{p}_{\eta_j}p_{\eta_j}}{Q_j}+\frac{\dot{p}_{\eta_M}p_{\eta_M}}{Q_M}\\
&=\left\{\left[\sum_{i=1}^N\frac{\mathbf{p}_i^2}{m_i}-3Nk_{\rm B}T\right]-\frac{p_{\eta_2}}{Q_2}p_{\eta_1}\right\}\frac{p_{\eta_1}}{Q_1}\\
&\ \ \ \ \ +\sum_{j=2}^{M-1}\left\{\left[\frac{p_{\eta_{j-1}}^2}{Q_{j-1}}-k_{\rm B}T\right]-\frac{p_{\eta_{j+1}}}{Q_{j+1}}p_{\eta_j}\right\}\frac{p_{\eta_j}}{Q_j}\\
&\ \ \ \ \ +\left\{\left[\frac{p_{\eta_{M-1}}^2}{Q_{M-1}}-k_{\rm B}T\right]\right\}\frac{p_{\eta_M}}{Q_M}\\
&=\left\{\left[\sum_{i=1}^N\frac{\mathbf{p}_i^2}{m_i}-3Nk_{\rm B}T\right]\right\}\frac{p_{\eta_1}}{Q_1}-k_{\rm B}T\sum_{j=2}^{M}\frac{p_{\eta_j}}{Q_j}\\
&=\left\{\left[\sum_{i=1}^N\frac{\mathbf{p}_i^2}{m_i}-3Nk_{\rm B}T\right]\right\}\dot{\eta}_1-k_{\rm B}T\sum_{j=2}^{M}\dot{\eta}_j\\
\end{align*}\tag{4.3}
$$

より，

$$
\begin{align*}
\dot{\mathcal{H}}&=0
\end{align*}\tag{4.4}
$$

Problem 13.5

Problem 5.9では周期ポテンシャル中を運動する単粒子を考えた。ここでは，更に線形ポテンシャル$${-fq}$$を系に追加し，粒子が一定力$${f}$$によって駆動されている状況を考える。この場合の全ポテンシャルはGalton’s staircaseとして知られている。

$$
\begin{align*}
U(q)&=V_0\cos(kq)-fq
\end{align*}
$$

a. エネルギーが一定に保たれる条件下における運動方程式を積分するプログラムを書き，長時間極限における$${\langle\dot{q}\rangle_t}$$を計算することによって系が定常状態に達しないことを示せ。

b. 次に系を$${k_{\rm B}T=1}$$のNose-Hoover chain熱浴と接続した場合を取り扱う。系は定常状態に達するであろうか？もしそうであるならば，様々な$${f}$$の値に対する$${\langle\dot{q}\rangle_t}$$を計算し，$${\langle\dot{q}\rangle_t}$$の$${f}$$に対する依存性が線形の領域を特定し，$${m=1,\ k=1,\ V_0=1}$$に選んだ場合の拡散係数$${D}$$の値を推定せよ。

c. 最後に，系をProblem 4.2の熱浴（$${M=2}$$とする）に接続した場合を考える。これらの方程式を積分するアルゴリズムはLiu and Tuckerman (2000)，及びEzra (2007)によって与えられた。(b)と同じ解析を実行し，様々な$${V_0}$$に対する拡散係数の値を推定せよ。

a. pythonにコード例を以下に示す。

import numpy as np
import random

### Input parameters ###
m         = 1
k         = 1
V_0       = 1
f         = 1
dt        = 0.001
n_steps   = 10000
n_samples = 1000
Total_E   = 1

### Define functions ###
def U(q, i):
    if i == 0:
        return V_0 * np.cos(k * q)
    else:
        return V_0 * np.cos(k * q) - f * q
    
def F(q):
    return k * V_0 * np.sin(k * q) + f
    
def E(q, v):
    return 0.5 * m * v ** 2 + U(q)
    
### The below is the code ###
# Generate the initial positions
vec_q = np.random.rand(n_samples)
vec_v = 2 * np.sqrt(Total_E - U(vec_q, 0)) / m 
vec_v *= np.array([random.randrange(-1, 2, 2) for _ in range(n_samples)]) 

# Integrate the equations of motion
for i in range(n_steps):
    # Update positions and velocities
    F_0 = F(vec_q)
    vec_q += dt * vec_v + 0.5 * dt ** 2 * F_0 / m
    F_1 = F(vec_q)
    vec_v += 0.5 * dt * (F_0 + F_1) / m
    
    # Print mean velocity
    print(f"{i}, {np.mean(vec_v)}")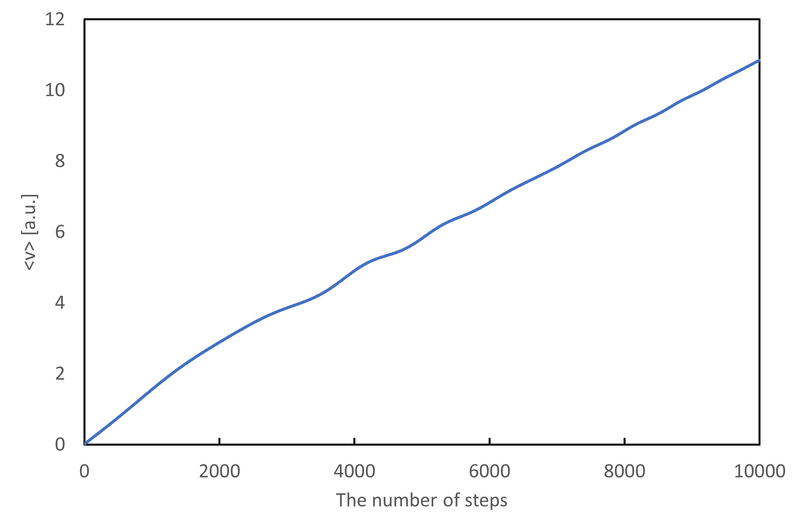

図 5.1にあるように$${\langle\dot{q}\rangle_t}$$は定常状態に達することなく増加し続ける。

b. pythonによるコード例を以下に示す。

### Import libraries ###
import numpy as np
import itertools

### Input parameters ###
N_c       = 4      # The number of decompotiosion for the operator exp(i * L_NHC * dt / 2)
dt        = 0.025  # time step
n_steps   = 5000   # The number of iteration
n_samples = 5000   # The number of samples for time average
M         = 2      # The number of chains
Q         = 1      # The time scale parameter for all chains
weight    = 1      # Weight of particle
k         = 1      # Wave number of periodic potential
V_0       = 1      # Height of periodic potential
f         = 1.00   # Driving force
kbT       = 1      # Temperature of thermostat

### Seven weights of the Yodhida scheme for a sixth-order scheme ###
N_sy = 7
w    = [0] * N_sy 
w[0] = w[6] = 0.784513610477560
w[1] = w[5] = 0.235573213359357
w[2] = w[4] = -1.17767998417887
w[3] = 1 - 2 * np.sum(w[:3])

### Initial values of dynamical variables ###
vec_q = np.random.rand(n_samples)
vec_p = np.random.normal(0, np.sqrt(weight * kbT), n_samples)
eta   = np.random.rand(M, n_samples)
p_eta = np.random.normal(0, np.sqrt(weight * kbT), ( M, n_samples))

### Define functions ###
def updateDynamicalVariables(p_now, eta, p_eta):
    for n_c, n_sy in itertools.product(range(N_c), range(N_sy)):
        scale = 1.0
        KE = p_now ** 2 / weight
        delta_j = w[n_sy] * dt / N_c
        p_eta[M - 1] += 0.25 * delta_j * (p_eta[M - 2] ** 2 / Q - kbT)
        for m in range(M - 2, -1, -1):
            p_eta[m] *= np.exp(-0.125 * delta_j * p_eta[m + 1] / Q)
            if m == 0:
                p_eta[m] += 0.25 * delta_j * (KE - kbT)
            else:
                p_eta[m] += 0.25 * delta_j * (p_eta[m - 1] ** 2 / Q - kbT)
            p_eta[m] *= np.exp(-0.125 * delta_j * p_eta[m + 1] / Q)
        
        scale *= np.exp(-0.5 * delta_j * p_eta[0] / Q)
        KE *= np.exp(-1.0 * delta_j * p_eta[0] / Q)
        
        for m in range(M):
            eta[m] += 0.5 * delta_j * p_eta[m] / Q
        
        for m in range(0, M - 1, 1):
            p_eta[m] *= np.exp(-0.125 * delta_j * p_eta[m + 1] / Q)
            if m == 0:
                p_eta[m] += 0.25 * delta_j * (KE - kbT)
            else:
                 p_eta[m] += 0.25 * delta_j * (p_eta[m - 1] ** 2 / Q - kbT)
            p_eta[m] *= np.exp(-0.125 * delta_j * p_eta[m + 1] / Q)

        p_eta[M - 1] += 0.25 * delta_j * (p_eta[M - 2] ** 2 / Q - kbT)
        
        p_now *= scale
    
    return p_now, eta, p_eta

def F(q):
    return k * V_0 * np.sin(k * q) + f

###---- The below is the code ----###
# The numerical integration
for i in range(1, n_steps + 1):
    vec_p, eta, p_eta = updateDynamicalVariables(vec_p, eta, p_eta)
    vec_p += 0.5 * dt * F(vec_q)
    vec_q += dt * vec_p / weight
    vec_p += 0.5 * dt * F(vec_q)
    vec_p, eta, p_eta = updateDynamicalVariables(vec_p, eta, p_eta)
    
    # Print mean velocity
    print(f"{i}, {np.mean(vec_p) / weight}")
    

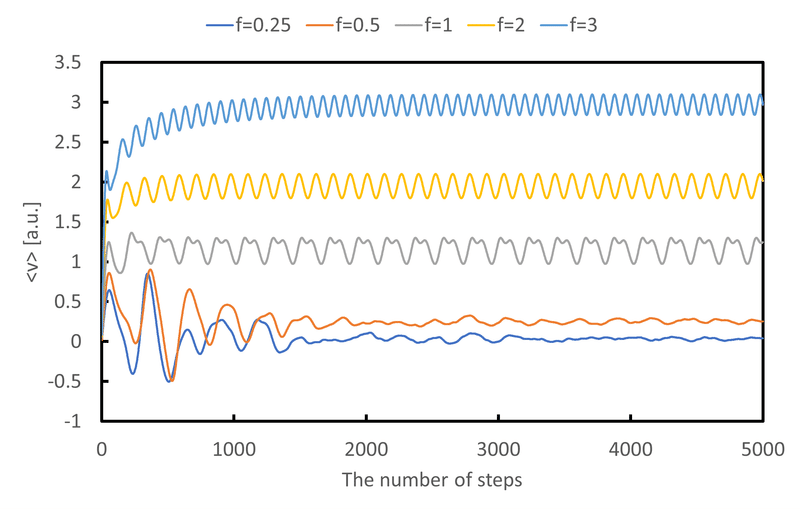
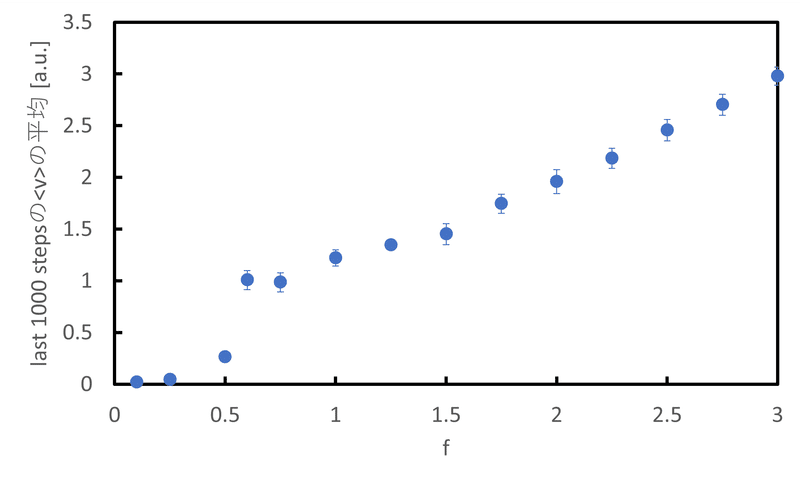
図5.3より，$${f=1.5}$$あたりから平均収束速度が$${f}$$に対して線形に応答している様子が伺える。拡散係数は$${D\simeq 1\ {\rm a.u.}}$$と見積もられる。

c. しんど過ぎるので省略。。。（せめて論文の中身を確認したい。。。）

Problem 13.6

(13.5.20)式のセル行列の発展が，(13.5.1)式で表さられる$${\mathbf{h}(0)={\rm diag}(L,L,L)}$$の場合のplanar Couette flowを再現することを示せ。

$$
\begin{align*}
\mathbf{h}(t) &=\begin{bmatrix}
L & \gamma t L & 0\\
0 & L & 0\\
0 & 0 & L
\end{bmatrix}
\end{align*}\tag{13.5.1}
$$

$$
\begin{align*}
\dot{\mathbf{h}} &= (\nabla\mathbf{u})^{\rm T}\mathbf{h}\\
\nabla\mathbf{u}&=\begin{bmatrix}
0 & 0 & 0\\
\gamma & 0 & 0\\
0 & 0 & 0
\end{bmatrix}
\end{align*}\tag{13.5.20}
$$

$$
\begin{align*}
\dot{\mathbf{h}} &= (\nabla\mathbf{u})^{\rm T}\mathbf{h}\\
&=\begin{bmatrix}
0 & \gamma & 0\\
0& 0 & 0\\
0 & 0 & 0
\end{bmatrix}
\begin{bmatrix}
h_{11} & h_{12} & h_{13}\\
h_{21}& h_{22} & h_{23}\\
h_{13} & h_{23} & h_{33}
\end{bmatrix}\\
&=\begin{bmatrix}
\gamma h_{21} & \gamma h_{22} & \gamma h_{23}\\
0& 0 & 0\\
0 & 0 & 0
\end{bmatrix}
\end{align*}\tag{6.1}
$$

より，

$$
\begin{align*}
h_{21} &= 0,&h_{22}&=L,&h_{23}&=0\\
h_{31} &= 0,&h_{32}&=0,&h_{33}&=L\\
\end{align*}\tag{6.2}
$$

また，(6.2)式より，

$$
\begin{align*}
\dot{h}_{11} &= 0, &\dot{h}_{12} &=\gamma L,&\dot{h}_{13}&=0\\
\therefore h_{11} &= L, &h_{12}&=\gamma tL, &h_{13}&=0\\
\end{align*}\tag{6.4}
$$

Problem 13.7

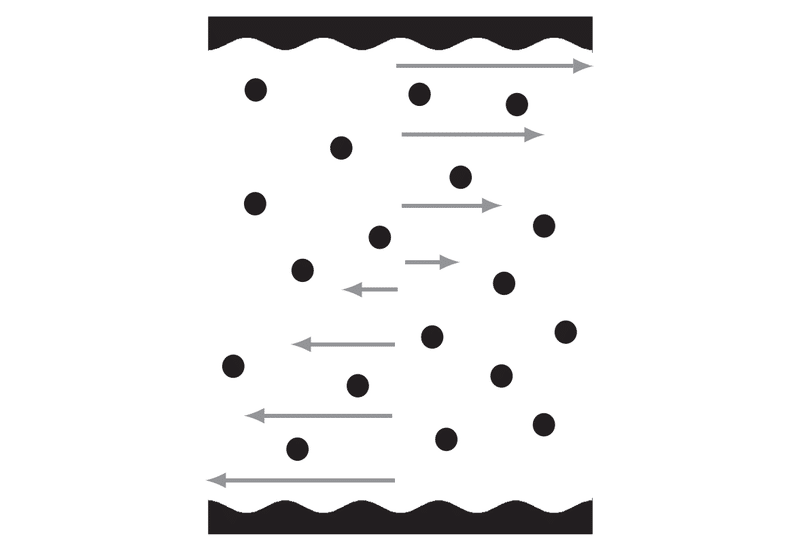
図13.8にあるような波形の板の間に閉じ込められた流体を考える。流体内の粒子は以下の運動方程式に従うとする。

$$
\begin{align*}
\dot{\mathbf{r}}_i&= \frac{\mathbf{p}_i}{m}\\
\dot{\mathbf{p}}_i&= \mathbf{F}_i+F_e\mathbf{e}_x
\end{align*}
$$

ここで，$${F_e}$$は定数であり，$${\mathbf{F}_i}$$は$${i}$$番目の粒子がそれ以外の粒子から受ける力と波形の板から受ける力を表す。定常状態における速度プロファイルを描画し，またその数式を与えよ。

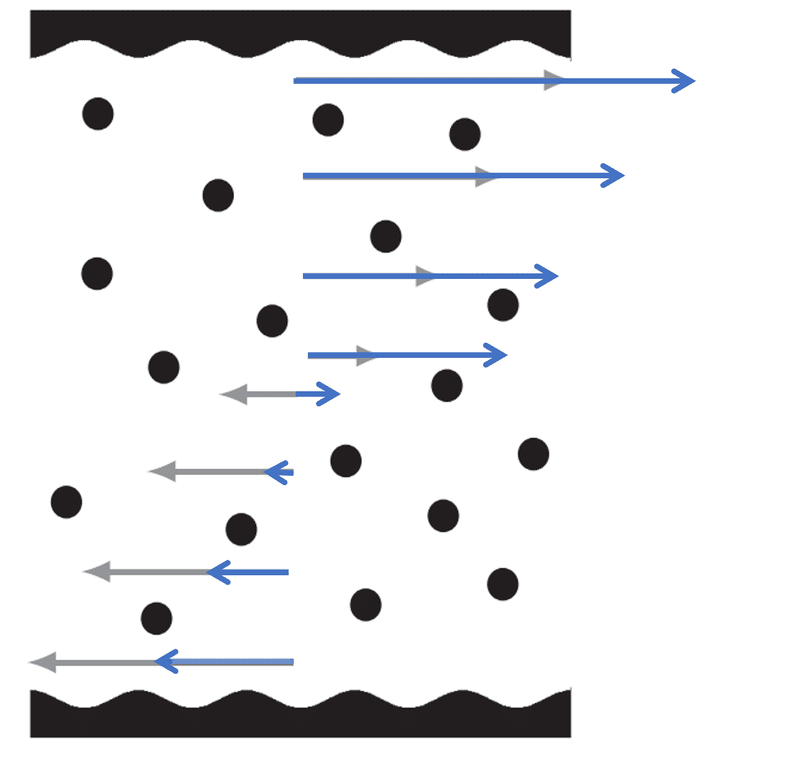
$$
\begin{align*}
v_x(y_{\rm surf})&=\gamma(y_{\rm surf}-y_0)-\frac{F_e}{S\lambda_{\rm surf}}
\end{align*}\tag{7.1}
$$

Problem 13.8

カノニカルアンサンブルでは$${\langle\mathcal{P}_{xy}\rangle=0}$$（圧力テンソルの非対角成分が0）になることを証明せよ。

圧力テンソル$${\mathbf{P}}$$のestimatorが

$$
\begin{align*}
\mathbf{P}&=\frac{k_{\rm B}T}{|\mathbf{h}|}\frac{\partial\ln Q}{\partial \mathbf{h}}\mathbf{h}^{\rm T}
\end{align*}\tag{8.1}
$$

で与えられること，及び体積$${V}$$に対するカノニカル分配関数$${Q(N,V,T)}$$とセルbox$${\mathbf{h}}$$に対する分配関数$${Q(N,\mathbf{h},T)}$$に

$$
\begin{align*}
Q(N,V,T)&=\int{\rm d}\mathbf{h} V^{-2} Q(N,\mathbf{h},T)\delta\left(|\mathbf{h}|-V\right)
\end{align*}\tag{8.2}
$$

が成立することを用いる。
(8.1)-(8.2)式より，圧力テンソルの期待値は，

$$
\begin{align*}
\langle\mathbf{P}\rangle&=\frac{1}{Q(N,V,T)}\int{\rm d}\mathbf{h} V^{-2} Q(N,\mathbf{h},T)\delta\left(|\mathbf{h}|-V\right)\mathbf{P}\\
&=\frac{k_{\rm B}T}{Q(N,V,T)V^2}\int{\rm d}\mathbf{h} Q(N,\mathbf{h},T)\frac{\delta\left(|\mathbf{h}|-V\right)}{|\mathbf{h}|}\frac{\partial\ln Q}{\partial \mathbf{h}}\mathbf{h}^{\rm T}\\
&=\frac{k_{\rm B}T}{Q(N,V,T)V^2}\int{\rm d}\mathbf{h} |\frac{\delta\left(|\mathbf{h}|-V\right)}{|\mathbf{h}|}\frac{\partial Q}{\partial \mathbf{h}}\mathbf{h}^{\rm T}\\
&=\frac{-k_{\rm B}T}{Q(N,V,T)V^2}\int{\rm d}\mathbf{h}Q(N,\mathbf{h},T) \frac{\partial}{\partial \mathbf{h}}\left\{\frac{\delta\left(|\mathbf{h}|-V\right)}{|\mathbf{h}|}\mathbf{h}^{\rm T}\right\}\\
\end{align*}\tag{8.3}
$$

となる。
$${\mathbf{h}}$$による微分の部分に着目すると，

$$
\begin{align*}
&\frac{\partial}{\partial \mathbf{h}}\left\{\frac{\delta\left(|\mathbf{h}|-V\right)}{|\mathbf{h}|}\mathbf{h}^{\rm T}\right\}\\
&=\frac{\delta\left(|\mathbf{h}|-V\right)}{|\mathbf{h}|}\mathbf{I}+\frac{\partial}{\partial \mathbf{h}}\left\{\frac{\delta\left(|\mathbf{h}|-V\right)}{|\mathbf{h}|}\right\}\mathbf{h}^{\rm T}\\
&=\frac{\delta\left(|\mathbf{h}|-V\right)}{|\mathbf{h}|}\mathbf{I}+\frac{\partial |\mathbf{h}|}{\partial \mathbf{h}}\frac{\partial }{\partial |\mathbf{h}|}\left\{\frac{\delta\left(|\mathbf{h}|-V\right)}{|\mathbf{h}|}\right\}\mathbf{h}^{\rm T}\\
&=\frac{\delta\left(|\mathbf{h}|-V\right)}{|\mathbf{h}|}\mathbf{I}+|\mathbf{h}|\left(\mathbf{h}^{-1}\right)^{\rm T}\frac{\partial }{\partial |\mathbf{h}|}\left\{\frac{\delta\left(|\mathbf{h}|-V\right)}{|\mathbf{h}|}\right\}\mathbf{h}^{\rm T}\\
&=\left[\frac{\delta\left(|\mathbf{h}|-V\right)}{|\mathbf{h}|}+|\mathbf{h}|\frac{\partial }{\partial |\mathbf{h}|}\left\{\frac{\delta\left(|\mathbf{h}|-V\right)}{|\mathbf{h}|}\right\}\right]\mathbf{I}
\end{align*}\tag{8.4}
$$

と計算されるため，$${\langle\mathbf{P}\rangle}$$は対角行列となることが分かる。

参考文献

1. Mark E. Tuckerman, Statistical Mechanics: Theory and Molecular Simulation (Oxford Graduate Texts)