こんにちは、freee株式会社でエンジニアをしているpokehです。

この記事は 裏freee developers Advent Calendar 2018 の9日目の記事です。
今日は社内で行われている圏論勉強会の話と、一ヶ月やってみた結果得た圏についての理解を書いてみようと思います。

はじまり

一ヶ月ほど前のある日のこと、チームの人たちが「cindy（私のニックネーム）に数学を教えてもらおう」などと談笑してました。しかし、一応数学科出身なものの、人に教えられるほど覚えてない。危機を感じた私は、あえて自分のやってこなかった分野を出すことで、責任から逃れようとします。

「教えることはできないですが、圏論の勉強とか、やってみたいですね」

これがチーム内外のHaskellersや数学好き、巻き込まれた人々にも広まり、次の週には
- 7人ほど参加者が集まり、
-「ゆっくり圏論勉強会」というGoogle Docとslackチャンネルが作成され、
- 毎週水曜の19:00-20:00の予定が確保され、
かくして我々は圏論習得への道を進むことになったのでした。

スピード感のあるチームですね／(^o^)＼
やるしかない。

勉強会、やるぞ

slackにどんどん集まるおすすめ資料。
とりあえず片っ端から目を通してみました。

- MacLaneの「圏論の基礎」
- Awodayの「圏論」
- 「ベーシック圏論」
- 「圏論の歩き方」
- 「プログラマーのための圏論」pdf
- 各種ブログやまとめ記事など...

我々はまず勉強会の第一回で「プログラマーのための圏論」の第二章を全員で読んでみました。ここで、これからどういう世界に踏みこむのか、イメージを膨らませていきました。
楽しい。

が、圏の定義はまだ出てきません。
これは圏論勉強会。圏論とは圏についての学問です。
我々は好奇心を募らせていきます。

第二回はその謎を解き明かすべく「俺が調べた圏の定義を聞け！」大会が実施されました。
ホワイトボードマーカーの奪い合い。熱中する議論。
なるほど、定義は理解した。
めっちゃ楽しい。

第三回・第四回は、アウディ本1.4章の色々な圏の具体例を見ていきます（なにしろ「ゆっくり」圏論勉強会です。ゆっくり進みます。）
有限集合と単射の写像の圏。証明して、理解したつもりになる。
半順序集合という圏。そういえば別の社内勉強会で、GitのコミットはInitial CommitをルートとしたDAG、つまりは半順序集合になるという話があったな。
しれっと、関手やモノイドの話が出てくる。それを読み流し次の章にいくと、群の話が出てきて、モノイドを理解しておくべきだったと気付く。

楽しい... けど、ちょっと難しい。

気付くと一ヶ月が経ちました。
果たして私は、圏とは何かが理解できているのか...？
というわけで、以下で説明してみます。

圏のイメージ

ところで皆さんは圏という字を見て、何を思い浮かべますか？
首都圏、文化圏、圏外。圏とは、「限られた地域や範囲」という意味のようです。

さらに、英語では圏論はCategory Theoryと言います。
カテゴリー... wikipediaはカテゴリーを「事柄の性質を区分する上でのもっとも基本的な分類」と説明しています。
日本語の圏とはちょっと違った印象ですが、繋がっては来ました。

ぼんやりと、圏論とは、世の中の有象無象のものをカテゴリー分けしてできた範囲のようなものを研究する分野だというイメージができてきました。

圏の定義

では自分の言葉で、圏の定義を書いてみます。

圏とは、以下の二つのもので表す何かです。
- 対象（object）
- 射（arrow）

射は、ある二つの対象の関係性を表します。
対象も射も、数はいくつあっても良いです。

イメージはこんな感じです。

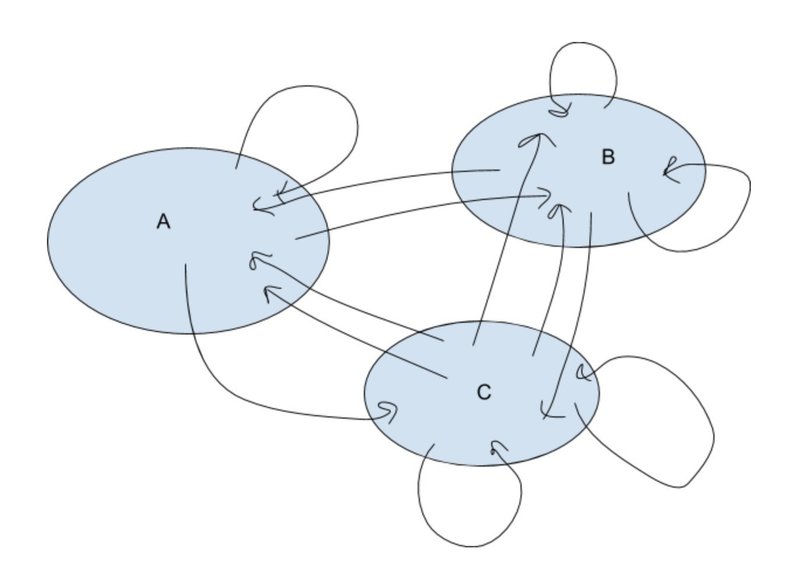
ただ、やみくもに丸と矢印だけを描くだけでは圏とは言えません。
圏であるためには、以下の3つのルールも満たす必要があります。

1. 射の合成が定義できる

圏論の世界では、合成とは二つの射を繋げることです。例えば対象Aから対象Bへの射fと、対象Bから対象Cへの射gを合成すると、対象Aから対象Cへの射ができます。その新しい射を合成と呼び、 g ∘ fと書きます。

より数学的な定義を以下に書きます。

まず前提として、対象A, B, C と射f, g, h で構成されている圏がある場合、f が A から B への射（ f : A → B と書く。）だとしたら、ドメイン（dom）とコドメイン（cod）は次のようになります。

dom(f) := A
cod(f) := B

要は、関係の元となる対象にdom、関係の先の対象にcodと名前をつけるだけです。
次が本題。圏では、f : A → B、g : B → C など dom(g) = cod(f) であれば、合成 g ∘ f という、A → C の関係性も定義できなければなりません。

2. 射の合成は、結合律を満たす

結合律とは、複数の演算の順番を変えても、その結果が変わらないという法則です。例えば整数の足し算「(1 + 2) + 3」と「1 + (2 + 3)」は両方とも6になります。これはどの整数を使っても同様なので、整数の足し算は結合律を満たします。

同様に、射の合成においても、たとえば f : A → B, g : B → C, h : C → D という三つの射がある場合、以下を満たさなければなりません。

(h∘g)∘ f = h∘ (g∘ f)

先にgとhを合成しても、先にfとgを合成しても、どちらも結果は変わらないということですね。

3. 射の合成は、単位律を満たす

単位律とは、結果を変えない存在があるという法則です。たとえば整数の足し算には0という存在があり、それに何を足しても結果が変わりません。

圏論の世界ではこの特別な射を恒等射といいます。これは圏の中の各対象に存在します。他と区別をつけるために、fやgではなく、idX（Xは対象名）と呼びましょう。

idはそれぞれ、任意の（合成可能な）射と合成しても、なにも結果を変えない射です。
たとえば f : A → Bとg : B → C、そして三つの恒等射 idA: A → A、idB : B →B、idC : C → C が存在する場合、以下のようになります。

f ∘ idA = f
idB ∘ f = f
g ∘ idB = g
idC ∘ g= g

（気をつけたいのが、たとえば  idA ∘ fという合成はできません。cod(f) と dom(idA) は等しくないからです。）

図の中だと、くるっと自分自身に戻っている射の一つが恒等射であるイメージです。ちなみに、定義から恒等射は、対象ごとにただ一つだけ存在することが示せます。

以上が三つのルールです。

このルールさえ満たしていれば、対象や射が何であっても等しく圏です。圏論の研究が進めば、その成果がすべての圏に適用できるということです。

関数型言語はまだ触ったことないのですが、この抽象化、特に射の合成のあたりは、プログラミング的にも色々都合が良さそうです。

色々な圏

個人的には、定義を知っただけではイメージができなかったので、次に色々な圏のイメージだけをお伝えしようと思います。

基本形の圏のイメージ、再掲。

要は、対象（A, B, C...）がいて、対象の間に射がいる。同じ対象に戻る射もあるし、別の対象への射もある。
ただのobjectとarrowです。それが何を表すかは一旦置いておきます。

対象というのは本当になんでもOKです。
なんなら、圏を対象としてもいい。下は「圏を対象とした、圏」のイメージです。

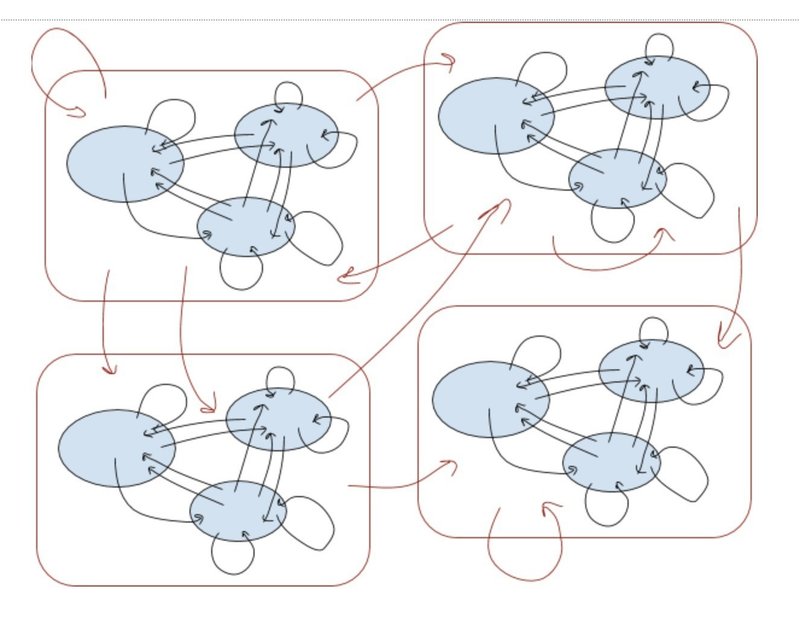
逆に、小さい圏も考えてみましょう。対象を一つだけにしたのがモノイドです。（射は複数あってもOK）

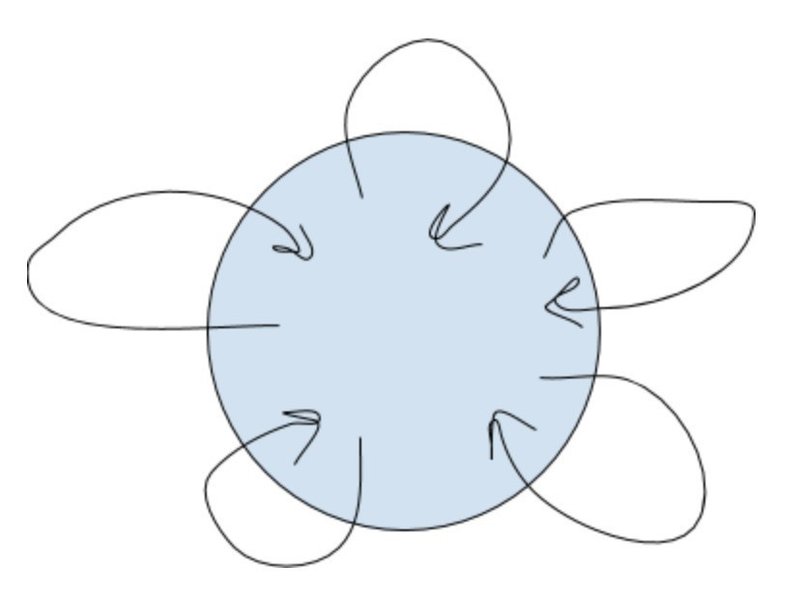
はたまた、対象は複数でも射の数を減らしたりしても、離散圏など色々な圏がつくれます。

ちなみに、これも圏です。

対象は一つ、射はない。これでも定義は満たせます。
趣深いですね。

ここらでネタ切れです。
ふわっとした説明になってしまいましたが、イメージだけでもお伝えできたなら幸いです。

最後に

この記事では、社内での圏論勉強会を通して私が理解した、圏の定義と色々な圏（のサイズ感）のイメージ共有を試みました。いかがでしたでしょうか。

本当はそろそろ忘却関手を理解して、10年前に好きだったラブソングの歌詞で、分かる部分が一つ増えた！と言いたいところですが、まだまだ道のりは長そうです↓

とはいえ、1人では確実にここまでも来れなかったです。
圏論勉強会、オススメです。毎週水曜が楽しみになっています。

さて、アドベントカレンダー。
明日はhim0さんです。最近社内でブームの脳波の話をしてくれるのか、はたまた別の切り口でやってくるのか。お楽しみに！