代表値とは、「全体の特徴を記述するために使われる1つの値」です。

例えば、「一人の日本人が1年で食べるお米の量は？」という調査があるとします。
1億件のデータが集まっても、眺めているだけでは分析は始まりません。
1億件のデータを”どのようにまとめるか”、
そこから”どのような傾向を見出すか”でデータに意味が現れてきます。

このように統計やデータ分析では、
たくさんのデータを”たくさんの個別データ”として扱うのではなく、
データの特徴を簡潔に表現できる数値を用いるほうが役立ちます。

今回は、この”データの特徴を表現できる数値”に関して3つの指標をご紹介いたします。
⚠今回から数式の記載があります。
⚠グラフや表は説明用に簡略なものを作成し掲載しています。

データの特徴を表現できる数値

（代表値のその前に）分布とは

分布とは広く散らばっていることを意味する。
データを散布図（下図）で表現すると”分布”していることがよく分かる。

もちろん、散布図以外にもデータの視覚的表現方法はいくつかある。

●度数分布表
一定のまとまりごとのデータの数を表で表すもの。

級間とは「一定のまとまり」のことを指し、上の例では10の級間がある。
度数とは「各級間に含まれるサンプル数」を指す。

量的変数の場合は、以下の式で最適な級間数を確認できる。

級間の幅 i とは「各級間の数値幅」となる。
度数分布表における級間数は10～20になるのがよいとされているため、上の例では次の式で10の級間とされた。

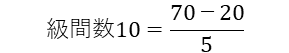
さらに、量的変数の級間には値の連続性が想定される。
上表で「20～25」「26～30」…というように整数で区切られているものの、
この整数値は名目上の限界（上限・下限）と呼ばれる。
真の上限・下限は「19.5～25.5」「25.5～30.5」…である。

質的変数の場合は、「級間の幅」などの考え方は適用できないため、
項目ごとに度数をまとめる。

●ヒストグラム（柱状図）
量的変数の度数分布表をグラフ化したものといえる。
下図のように棒グラフに類似しているが、
量的変数は数値間に連続性があるため、
各棒の間は隙間なく詰められている。

●棒グラフ
質的変数の度数分布表をグラフ化したものといえる。

●円グラフ
質的変数の度数分布表をグラフ化したものといえる。
棒グラフと異なり、全体に占める各項目の割合で構成される。

平均値

量的変数データの総和をデータ件数で割った商。

左辺が平均値を表し、エックスバーと読む。
また、Nはデータ件数、Xは測定値、∑（シグマ）は加算記号を表す。
したがって上式では、
「平均値は、データ中の測定値（X）を総和して、データ件数で割った商」であることを意味する。

例えば、［1, 2, 3, 4, 5］というデータがあった場合、

式4の結果、平均値は【3】とわかる。

データ分析や検定、多変量解析などの分野では多用される平均値ではあるが、次のような特徴を有している。

①偏差の和は0になる。

偏差とは「測定値と平均値の差」を意味し、上式の左辺を指す。
式4のデータを当てはめると、

②外れ値の影響を強く受ける。
外れ値とは、データ分布全体を見たときに極端に外れている値を指す。

例えば、ある地域の年収額を調査したとして、
[300万円, 300万円, 300万円, 300万円, 1億円]となったとする。
平均値は【2000万円】ほどになるが、実態を代表しているとは言えない。

③測定値と平均値の差の総和は”0”になる
「測定値と平均値の差」を偏差（平均偏差）と呼ぶ。
この偏差の総和（＝偏差和）が0となる特性も持つ。

例えば、[300万円, 300万円, 300万円, 300万円, 1億円]の場合、
偏差和＝((300-2000240)+(300-2000240)+(300-2000240)+(300-2000240)+(10000000-2000240))=0
となる。

このように極端な値が混ざることによって、
その極端なデータに引っ張られてしまうことがある。
この対策として、変数同士を組み合わせた合成変数や、
次回に出てくる【分散や標準偏差】を使用して外れ値を除去する。

平均値は他にも統計的に有利な特性を持っているが、ここでは割愛する。

中央値

1つの分布のちょうど真ん中に位置する度数の値。
中央値を算出するパターンとしては以下の4パターンが想定される。

①中央値付近の同点がなく、分布が奇数個
例：[3, 5, 6, 7, 8]の場合　→　分布中央はの[3, 5, ⑥, 7, 8]　⇒　6が中央値

②中央値付近に同点がなく、分布が偶数個
例：[3, 5, 6, 7]の場合　→　分布中央は[3, 5, ◯, 6, 7]となる
→　◯の左右の測定値の中央となる　→　（5+6）/2＝5.5　⇒　5.5が中央値

③中央値付近に同点があり、分布が奇数個
例：[2, 4, 5, 7, 7, 7, 9, 10, 11]の場合　→　N=9　→　9/2＝4.5
→　分布の両端から【4.5個目】に中央値が存在する。

図左側の【4.5】の部分には[2, 4, 5]の3件が含まれている　→　4.5－3＝1.5
→　「7」3個分を1.5個とった値が中央値となる
→　「7」の真の下限値は「6.5」　かつ　1.5/3＝0.5　→　6.5+0.5＝7
⇒　7が中央値

④中央値付近に同点があり、分布が偶数個
例：[3, 5, 6, 8, 8, 8, 9, 9, 11, 12]の場合　→　N=10　→　10/2＝5
→　分布の両端から【5個目】に中央値が存在する。

図左側の【5】の部分には[3, 5, 6]の3件が含まれている　→　5－3＝2
→　「8」3個分を2個とった値が中央値となる
→　「8」の真の下限値は「7.5」　かつ　2/3＝0.67　→　7.5+0.67＝8.17
⇒　8.17が中央値

中央値の算出を公式化したものが以下である。

Lは中央値を含む値の真の下限値、
iは級間の幅、
FはL以下の累積度数、
分母のfは中央値を含む級間の度数となる。

例えば、④の[3, 5, 6, 8, 8, 8, 9, 9, 11, 12]を当てはまると、
L＝7.5、i=1、F=3、f=3となる。

また、平均値の最後に挙げた年収の例で計算すると、
[300万円, 300万円, 300万円, 300万円, 1億円]なので、
L＝299.5、i=1、F=0、f=4となる。

中央値は【300.125万円】となり、実態を代表していそうである。

最頻値

最も度数が多い測定値。
[3, 5, 6, 8, 8, 8, 9, 9, 11, 12]であれば【8】が最頻値となり、
[3, 5, 8, 8, 8, 9, 11, 11, 11, 12]であれば【8】と【11】が最頻値となる。
なお後者の場合は、特に両最頻値分布と呼ばれる。

次回のnote

次では「分散と標準偏差」に関して紹介します。

参考文献

南風原朝和（2012）．心理統計学の基礎 統合的理解のために　有斐閣アルマ

繁桝算男・柳井晴夫・森敏昭（編者）（2008）．Q&Aで知る 統計データ解析［第2版］ーDOs and DON'Tsー　サイエンス社

田中敏・山際勇一（1992）. 新訂　ユーザーのための教育・心理統計と実験計画法　方法の理解から論文の書き方まで　教育出版

山内光哉（2011）．心理・教育のための統計法〈第3版〉　サイエンス社