まず、コラッツの問題とはなんぞや。

とてもシンプルですね。任意の正の整数 nに対して、
１．　n が偶数の場合、n を 2 で割る
２．　n が奇数の場合、n に 3 をかけて 1 を足す
この単純な操作で、どんな初期値でも必ず 1 に到達するんですね。

例えば、３→１０→５→１６→８→４→２→１となります。
これを見ただけでも勘のいい人なら、２の乗数になった時点で、確実に１に到達することや、何やら５の倍数も怪しげだな。。。と思っているかもしれません。

では、実際に１５はどうかというと、、、
１５→４６→２３→７０→３５→１０６→５３→１６０→８０→４０→２０→１０→以下略

予想以上に工程数がかかります。が、１に到達します。
また、ここでも１６０、８０、４０、２０、１０と、２の乗数×５は全て収束することを証明できそうです。拡張すれば、２の乗数×任意の正の整数 nは、nが既出で収束していれば、探索不要であることがわかります。
なんなら、１から順に探索する場合、n が偶数の場合、n を 2 で割る初手で、必ず既出のnになるので、探索不要なわけです。

一方で、ルールを変えて試してみると、
任意の正の整数 nに対して、
１．　n が偶数の場合、n を 2 で割る
２．　n が奇数の場合、n に 3 をかけて 1 を引く
ルールにするとどうなるのか。
例えば、３→８→４→２→１、５→１４→７→２０→１０→５と早くもループになり成立しません。

PythonでCollatzのコードを書いている人がたくさんいらっしゃったので、参考に書いてみた。

なにはともあれ出てくる数字の解析するためのcsvを作るために、全探索版とスキップ版を作りましたが、スキップ版のみ例示しておきます。
下手くそなので、スパゲッティコードなので悪しからず。

# coding: utf-8
# Your code here!
import csv
import io

from google.colab import drive
drive.mount('/content/drive')

import sys
sys.path.append('/content/drive/My Drive/colab/Collatzdata')

import os

def Collatz(n):
    if n % 2 == 0:
        return int(n /2)
    elif n % 2 == 1:
        return int(3 * n + 1)

def CollatzCycle(n):
    init = n
    m = 0
    C_list=[]
    skip_list=[]
    while Collatz(n)!=0:
        if not n in skip_list_all:
            n = Collatz(n)
            m += 1
            C_list.append(str(n))
            skip_list.append(n)
            if n == 1:
                csv_path = '/content/drive/My Drive/colab/Collatzdata/Collatz_skip_1_100000.csv'
                C_list.insert(0,str(init))
                C_list.insert(0,str(m))
                #print(C_list)
                with open(csv_path, 'a', newline='') as file:
                    writer = csv.writer(file)
                    writer.writerow(C_list)
                break
        else:
            #print('skip:'+ str(init))
            #print('cycle:'+ str(m))
            #print('due to:'+ str(n))
            skip_list.append(init)
            csv_path = '/content/drive/My Drive/colab/Collatzdata/Collatz_skip_1_100000.csv'
            C_list.insert(0,str(init))
            C_list.insert(0,str(m))
            #print(C_list)
            with open(csv_path, 'a', newline='') as file:
                writer = csv.writer(file)
                writer.writerow(C_list)
            break

    return skip_list

skip_list_all = []

for n in range(1, 100000):
    #print('num:'+ str(n))
    if n in skip_list_all:
        print('skip:'+ str(n))

    else:
        skip_list = CollatzCycle(n)
        skip_list_all.extend(skip_list)
        skip_set = set(skip_list_all)
        skip_list_all = list(skip_set)
        #print(skip_list_all)

本題はここから。コラッツの問題で出てくる数字についてPythonで解析してみるコードとともに、解説していきます。
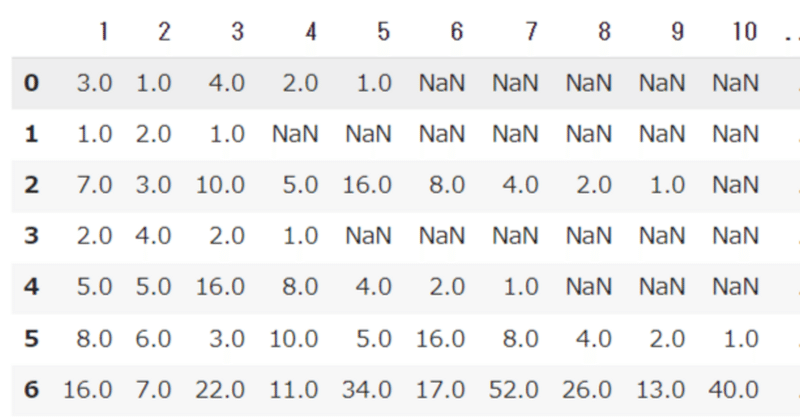
csvのまとめ方を工夫すれば良かったのですが、保存形式を１列目に工程数、２列目に初期値、以降は１になるまでのコラッツ数列を記録したので、列数がまちまちになってしまいました。そのままだとread_csvで読み込めません。なので、col_name = range(1,1000,1)で適当に列名を１から順に１０００列番号で振って、数字がないとこはNaNとして読み込んで、dropnaでNaNしかない列は全消ししてます。

import pandas as pd 

col_name = range(1,1000,1)
df = pd.read_csv("Collatz_1_10000.csv", names=col_name,encoding="utf_8", na_values='----', dtype = 'float')
dfv2 = df.dropna(how='all', axis=1)

これでまぁまぁなんとかいろいろと、処理できそうな形式にできました。

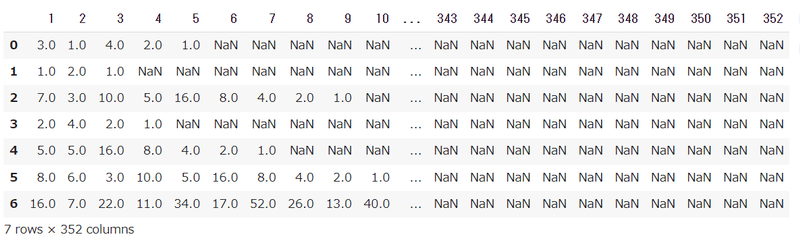
まずは１列目の解析から。１に収束する（スキップ版の場合は既出の数字になる）までの工程数は、何回が一番多いのかについて。

import collections
import csv
data = list(dfv2[1])
c = collections.Counter(data)
# 数の出現回数を表示します。
# most_common()は、最も多い要素から順に表示するメソッドです。
for _ in c.most_common():
    #print(_)
    csv_name = '/content/drive/My Drive/colab/Collatzdata/Collatz_1_100000_commonrank.csv'
    with open(csv_name, 'a', newline='') as file:
        writer = csv.writer(file)
        writer.writerow(_)

列名を数字とカウントとして読み込みます。

col_name = ['num','count']
df_CR = pd.read_csv("Collatz_1_100000_commonrank.csv", names=col_name,encoding="utf_8", dtype = 'int')

結果はご覧のとおり、７１工程で収束することが多いようです。それにしても、パッと見ただけでも１４６以外は７０±２０の工程数の頻度がやけに多いですね。不自然すぎる。。。次回は７１工程で収束する頻度が、整数 nがいくつ以上でそうなるのか見てみたいところ、あとは、逆に収束工程数として出てこない数字も気になる。

カウント数の減衰傾向も見てみた。

from matplotlib import pyplot as plt
df_CR['count'].plot(kind='line', figsize=(8, 4), title='count')
plt.gca().spines[['top', 'right']].set_visible(False)

二次関数っぽいので、近似曲線を求めてみる。このとき、少ないカウント数を入れると、精度が悪くなる気がしたので、出現回数上位半分に絞って、近似式を求める。

 #二次関数で多項式近似を行う 
import numpy.polynomial.polynomial as P
majority = len(df_CR['count']) * 0.5
df_CR_main = df_CR[:int(majority)]
X_main = range(1, len(df_CR_main['count'])+1, 1)
coef = P.polyfit(X_main, df_CR_main['count'], 2)

# 作成した多項式近似を表示
print('y = ' + str(coef[0]) + ' + ' + str(coef[1]) + ' * x + ' + str(coef[2]) + ' * x^2')

y = 1259 + -12.61 * x + 0.03955 * x^2
参考までに、全データを使った場合は、y = 1164 + -9.028 * x + 0.01744 * x^2になる。

近似曲線を重ねてみる。

# 作成した近似曲線の(x, y)の組み合わせを求める
x = np.arange(1, len(df_CR_main['count'])+1, 1)
y = P.polyval(x, coef)
X = range(1, len(df_CR['count'])+1, 1)
# 元データと近似曲線をプロット
fig, ax = plt.subplots()
ax.scatter(X, df_CR['count'],label='obs')
ax.plot(X_main, y,label='model_2ndorder', color="m")
ax.set_ylabel('count')
ax.set_title('count')
plt.legend()
plt.show()

まぁ悪くなさそう。

収束回数の数字の出現傾向、ノイズっぽくも見えるし、右から左に見ると、減衰振動の重ね合わせっぽくも見える。

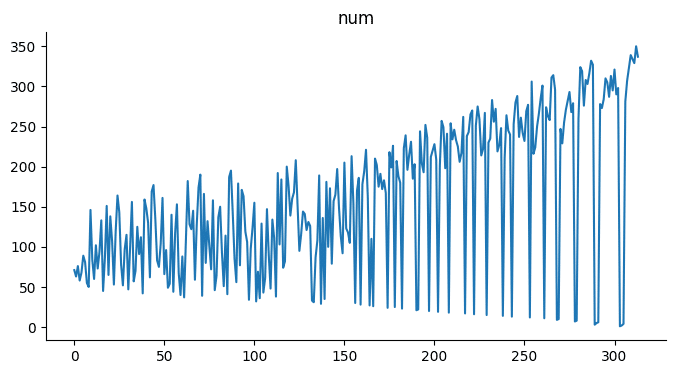
フーリエ変換してみた。（出現回数上位半分に絞っている）

N = len(df_CR_main['num'])
fw = np.fft.fft(df_CR_main['num'])
freq = np.fft.fftfreq(N, 1)
# FFTの複素数結果を絶対値に変換
fw_abs = np.abs(fw)
# 振幅をもとの信号に揃える
fw_abs_a = fw_abs / N * 2 # 交流成分はデータ数で割って2倍
fw_abs_a[0] = fw_abs_a[0] / 2 # 直流成分は2倍不要
plt.scatter(freq, fw_abs_a,s=1,label='obs', c = 'b')
plt.plot(freq, fw_abs_a,label='model_abs', color="m", alpha=0.5)
#plt.plot(freq, fw,label='model', color="y", alpha=0.5)
plt.legend()
plt.show()

これは、入力信号が1つの正弦波っぽいですね。サイドバンドっぽいの見えてますが。

さらにいろいろとフィルタリング処理してみる。

fw2 = np.copy(fw)
# フィルタリング処理
fc =  0.1 # カットオフ（周波数）
fw2[(freq > fc)] = 0 # カットオフを超える周波数のデータをゼロにする（ノイズ除去）
# フィルタリング処理したFFT結果の確認
# FFTの複素数結果を絶対値に変換
fw2_a = np.abs(fw2)
# 振幅をもとの信号に揃える
fw2_a_a = fw2_a / N * 2 # 交流成分はデータ数で割って2倍
fw2_a_a[0] = fw2_a_a[0] / 2 # 直流成分（今回は扱わないけど）は2倍不要

# グラフ表示（FFT解析結果）
plt.plot(freq, fw2_a_a, c='r')

右側の大半をノイズとしてカットした。

逆フーリエ変換にかけて、元の図と重ねて見ると。。。

# 周波数でフィルタリング（ノイズ除去）-> IFFT
fw2_ifft_f = np.fft.ifft(fw2) # IFFT
fw2_ifft_f_real = fw2_ifft_f.real 
# グラフ表示：オリジナルとフィルタリング（ノイズ除去）
plt.plot(X, df_CR['num'], label='original')
plt.plot(X_main, fw2_ifft_f_real, c="r", linewidth=1, alpha=0.7, label='filtered')

うーんイマイチ。。。

いっそ両側をカットしてみると。

fw2 = np.copy(fw)
# フィルタリング処理
fc =  0.1 # カットオフ（周波数）
fw2[(freq > fc)] = 0 # カットオフを超える周波数のデータをゼロにする（ノイズ除去）
fc =  -0.1 # カットオフ（周波数）
fw2[(freq < fc)] = 0 # カットオフを超える周波数のデータをゼロにする（ノイズ除去）
# フィルタリング処理したFFT結果の確認
# FFTの複素数結果を絶対値に変換
fw2_a = np.abs(fw2)
# 振幅をもとの信号に揃える
fw2_a_a = fw2_a / N * 2 # 交流成分はデータ数で割って2倍
fw2_a_a[0] = fw2_a_a[0] / 2 # 直流成分（今回は扱わないけど）は2倍不要

# グラフ表示（FFT解析結果）
plt.plot(freq, fw2_a_a, c='r')

同様に 逆フーリエ変換にかけて、元の図と重ねて見ると。。。※振幅倍にして１００引いて見やすくしてます。

# 周波数でフィルタリング（ノイズ除去）-> IFFT
fw2_ifft_all = np.fft.ifft(fw2) # IFFT
fw2_ifft_all_real = fw2_ifft_all.real * 2 - 100 # 実数部の取得、振幅をいじる
# グラフ表示：オリジナルとフィルタリング（ノイズ除去）
plt.plot(X, df_CR['num'], label='original')
plt.plot(X_main, fw2_ifft_all_real, c="r", linewidth=1, alpha=0.7, label='filtered')

これはこれで近似し過ぎか。。。？まぁでも、傾向が見えてきそうな気がする。それにしてもなんなんだこの不気味な振動する感じは。。。

王道の収束回数の数字を横軸に、そのカウント数を縦軸に並べてみる。

from matplotlib import pyplot as plt
df_CR_main.plot(kind='scatter', x='num', y='count', s=32, alpha=.8)
plt.gca().spines[['top', 'right',]].set_visible(False) 

複雑な分布図にも見えるけど、想像以上にきれいにも見える。少なくとも２つの山が心の目で見ると見える。これはなにかありそうな気がする。。。

カウント数の分布を見てみる。

import numpy as np
import matplotlib.pyplot as plt
# Plot histogram
data = list(dfv2_z[1])
fig, ax = plt.subplots()
ax.hist(data, bins=np.arange(max(data)), ec='white')
ax.set(xlabel='values', ylabel='Frequency', title='Distribution of x')

先の散布図のほうが、なにか見えてきそう。。。

その他王道の平均値ほかの分布など。これもどのくらいの値を調べると、値が収束し始めるのかとか調べてみたいところなので、次回はスキップ版のついでに調べてみようと思う。
平均的には１０７回で１に収束する模様。頻度が多い収束までの工程数が７１回なので、今後、探索数を増やしていくと、頻度が多い工程数がもっと大きな数字に置き換わる可能性があるのかもしれない。そのあたりも、探索数を増やしたときに、平均値がどっちに引っ張られるかを調べると、なにか面白そう。あとで、最大の３５０工程かけないと収束しなかった数字は調べよう。特に後で調べる全体の出現した数字の最大値と関係しているのかは気になるところ。

import scipy.stats as stats
print('平均値：', np.mean(data))
print('中央値：', np.median(data))
print('合計：', np.sum(data))
print('分散',np.var(data,ddof=1))
print('標準偏差',np.std(data,ddof=1))
print('最大',np.max(data))
print('最小',np.min(data))
print('四分位点(25%)：', np.percentile(data, 25))
print('四分位点(50%)：', np.percentile(data, 50))
print('四分位点(75%)：', np.percentile(data, 75))
print('最頻値：', stats.mode(data))

平均値： 107.53822538225383
中央値： 99.0
合計： 10753715
分散 2638.4733858024797
標準偏差 51.36607232213185
最大 350
最小 1
四分位点(25%)： 65.0
四分位点(50%)： 99.0
四分位点(75%)： 146.0
最頻値： ModeResult(mode=71, count=1467)

そして、やっとこ全体の出現した数字に付いての調査をする。csvの形式がややこしいので、まず、工程数の列を消して、１行ずつ処理していく。０以外の数字を片っ端からリストにぶっ込んでいく。できあがった全体の出現した数字リストから、どの数字が一番出現頻度多いのかについて調べる。

import itertools

_data = dfv2_z.drop(df.columns[[1, 0]], axis=1).values
dlist = []
dlist += [[e for e in row if e!=0] for row in _data.tolist()]

data = list(itertools.chain.from_iterable(dlist))

import collections
import csv
c = collections.Counter(data)
# 数の出現回数を表示します。
# most_common()は、最も多い要素から順に表示するメソッドです。
for _ in c.most_common(100000):
    #print(_)
    csv_name = '/content/drive/My Drive/colab/Collatzdata/Collatz_1_100000_all_commonrank.csv'
    with open(csv_name, 'a', newline='') as file:
        writer = csv.writer(file)
        writer.writerow(_)

今回は王道の平均値ほかなどかから調べる。
平均値はほとんど意味がなさそうです。標準偏差の値も大きすぎる。中央値と平均値の差もでかい。ただ、最大値は１０億を超えていて、そこは面白いところ。最頻値が１なのも特に面白みがない。

print('平均値：', np.mean(data))
print('中央値：', np.median(data))
print('合計：', np.sum(data))
print('分散',np.var(data,ddof=1))
print('標準偏差',np.std(data,ddof=1))
print('最大',np.max(data))
print('最小',np.min(data))
print('四分位点(25%)：', np.percentile(data, 25))
print('四分位点(50%)：', np.percentile(data, 50))
print('四分位点(75%)：', np.percentile(data, 75))
print('最頻値：', stats.mode(data))

平均値： 58877.45558730169
中央値： 1186.0
合計： 633151377311
分散 2177390641710.5784
標準偏差 1475598.401229338
最大 1570824736
最小 1
四分位点(25%)： 182.0
四分位点(50%)： 1186.0
四分位点(75%)： 10705.0
最頻値： ModeResult(mode=1, count=99999)

列名を数字とカウントとして読み込みます。

col_name = ['num','count']
df_all_CR = pd.read_csv("Collatz_1_100000_all_commonrank.csv", names=col_name,encoding="utf_8", dtype = 'int')
#_df = df.fillna('')
#dfv2 = df.dropna(how='all', axis=1)
#dfv2.head(7)

df_all_CR.head(50)

結果はご覧のとおり、１、２、４、８、１６がトップ５で出現頻度が多いようです。まぁ収束ルート上にいるので、当然といえば当然ですが。。。ただ、次は３２ではなく、５が来ます。

１６の次に５が多い理由を考えてみると、コラッツのルールである３倍して１を足すときに、５と１６はズブズブの関係ですね。３２から１を引くと、３１なので、３倍して１を足すルートからは到達できませんので、必然的に、６４からしか到達できないので、途端に出現頻度が下がるのでしょう。
とはいえ、５の出現頻度がここまで多いのも、なにか理由がありそう。５から１を引くと、４は奇数（24/2/14修正）なので、３倍して１を足すルートからは到達できませんので、そこは３２と同じです。必然的に、１０からしか到達できないので、途端に出現頻度が下がってもいい気がします。では、５の次に多い１０の出現頻度はというと、１０から１を引くと、９なので、３から３倍して１を足すルートで到達できます。しかし、３の出現頻度はトップ５０にすら入っていません。
では、２０の出現頻度はというと、２０から１を引くと、１９なので、３倍して１を足すルートから到達できませんので、必然的に、４０からしか到達できません。
では、４０の出現頻度はというと、４０から１を引くと、３９なので、１３から３倍して１を足すルートから到達できます。
では、１３の出現頻度はというと、、、

これ以上はキリがなさそうなので、続きはまた次回ほかの解析と合わせて、やってみます。それにしても、この出現頻度の数字の表は、調べて見ると、なかなかに沼ですがなにかありそう。