東大IPMUの立川さん@yujitach が下記の記事をアップされたので、少しコメントをしておこうと思います。
追記(2023/11/28）：その後立川さんと長い議論をして頂き、より整理が付いたので加筆修正をしました。

私の教科書では、実験で観測できる物理量の確率分布こそが量子力学の基礎であり、状態ベクトルや波動関数や密度行列はその１つの表記に過ぎないことを強調しています。

これは電磁気学のマクスウェル方程式を４元数や外微分形式でも表すことができるのと同じ意味であり、ベクトルや行列や演算子は量子力学の表し方の１つでしかありません。最初に物理量の確率分布の集まりから量子状態は定義されます。教科書では、その後で量子状態トモグラフィ法によって、量子状態が密度行列で表示される流れになっています。そしてその密度行列の特別な例として、その行列のスペクトル表示が１つの状態ベクトルだけで書ける量子状態を採り上げて、それを純粋状態であると定義します。波動関数は点粒子の純粋状態での状態ベクトルの１つの成分表示に過ぎません。ですから状態ベクトルや波動関数のみならず、密度行列も、確率論で量子状態を定義した後に導入された「記述の便法」だという内容になります。

立川さんは数理物理学の観点から「密度行列が先」派と「状態ベクトルが先」派という名前を記事で導入されていますが、私自身はそのどちらでもなく「観測される物理量の確率分布こそが先」派ということになります。

量子に限らず一般に確率分布は、観測によって情報が更新された結果として収縮を起こすため、状態ベクトルや波動関数も観測で収縮するのは当たり前になります。その結果、前世紀に散々議論されたのに何も身のある結果を出さなかった「観測問題」は、そもそも存在しなかったのだと分かるのです。

立川さんは確率分布による定式化よりも、密度行列と状態ベクトルでの定式化の差に特化して記事を書かれています。特にベリー位相という数学のトポロジーに関係した面白い物理現象に関して考察をされています。

ベリー位相とは量子系のハミルトニアンを非常にゆっくりと変形をして、最後には元のハミルトニアンに戻す過程で現れる、エネルギー固有状態のベクトルにかかる位相因子のことです。立川さんのノートにもありますように、量子多体系でのボルン=オッペンハイマー近似において、ゆっくり動く自由度へ速く動く自由度のダイナミクスが与える位相因子であるとも説明ができます。

立川さんがノートの後半で使われた例を用いて、少し具体的にみてみましょう。ゆっくり動く自由度が3次元のクラインの壷の空間上での二準位スピン粒子となった例です。その波動関数を

と書くことにします。そしてボルン=オッペンハイマー近似で出てくるそのシュレディンガー方程式は、ベリー接続場を伴った

という形になったとします。空間はクラインの壷なので、各空間座標の値には

という周期性と

というトポロジー的な捻りをいれた同一視が課せられます。

なお２準位スピンを考えているので、以降では

というパウリ行列を使います。この各成分の量子力学的な期待値は

で計算をされます。この設定において、各期待値に対する立川さんの境界条件は次の３つになります。

立川さんのノートではこの期待値の境界条件を満たすように、波動関数へ次の３つの境界条件を課しています。

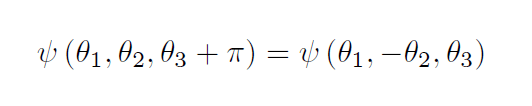
そして以下のような矛盾によって、この３つの境界条件が同時に満たされることはないことを、立川さんはノートで証明されました。まず先に第１方向の周期性条件を使ってから、その次に第３方向の捻りの条件を使うことで、以下のように波動関数を計算します。

一方で第３方向の捻りの変形を先にしてから第１方向の周期性条件を使うと、同じ波動関数なのに第２方向の位置座標に依存した位相因子が異なる結果になり、矛盾が起きています。

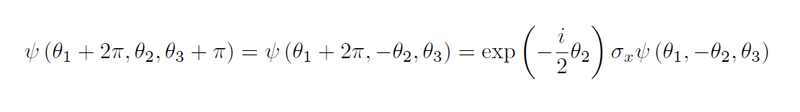
このため（４）式、（５）式、（６）式の周期境界条件を満たす波動関数やそれに対応する状態ベクトルは存在しないことがわかります。

この立川さんの結果は数理物理として非常に面白いと思いますが、この結果は密度行列からも導けます。同じような解析で同じ矛盾を次のように示せるるからです。

まず重要なことは、ボルン=オッペンハイマー近似ではゆっくり動く座標自由度も平等に物理量としてみなす点です。トポロジーを通じて空間自由度とスピン自由度が密接に絡んでいるので、スピン自由度だけを取り出して扱うことはできないのです。したがって密度行列ρの引数として、以下のように空間自由度も採り入れなければなりません。

このρに対して先に第１方向の周期性条件を使って、次に第３方向の捻りの条件を使うと、空間第２方向の位置座標に依存する位相因子が出てきます。

同じρで第３方向の捻りの変形をしてから第１方向の周期性条件を使うと、以下のようになります。

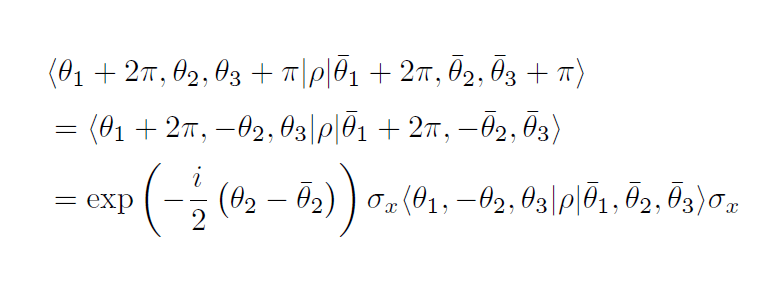
同じ密度行列であるべきなのに２つの等式で空間第２方向の位置座標に依存する位相因子が異なるため、波動関数と同様に矛盾が証明できました。つまり「密度行列が先」派でも「状態ベクトルが先」派でも良いのです。

なおこのクラインの壷での粒子の理論を、ベリー位相の理論のように物性系に埋め込まれた一部の自由度に対する近似としてみなす場合と、純粋数学的にSU(2)非可換ゲージ理論とみなす場合では、観測量の定義が変わることには注意をしてください。物性系ならば二準位スピンのパウリ行列は観測可能な物理量としてみなされます。この立場ではスピン成分の各期待値も物理量ですから、クラインの壷の上では１価でなければなりません。なので立川さんがスピン成分に設定をした（１）式、（２）式の２価条件は物理の実験では決して実現をしません。クライン壷空間といえど、物理量の期待値は１つの値にきちんと定まるのですから、矛盾が生じるのです。

（註：物性の結晶系で出てくる波数空間でのブリルアン・ゾーンの同一視で、トーラスのトポロジーを考える場合などとは、この議論は区別をしてください。結晶系の物理は本物のトーラス空間での量子力学の物理ではなく、大きな波数のブリルアン・ゾーンと小さな波数のブリルアン・ゾーンを数学的に同一視をしているだけです。ですから波数空間のトーラス上で多価の関数や物理量を考えることもできます。しかし実際の物理実験では、それぞれ異なる波数を直接測定で区別できるので、本当に１つのトーラス空間を想定しているわけではありません。カットの入ったリーマン面のように、異なるトーラスが無数に繋がっている状況に過ぎません。）

しかし物性系の理論ではなく、純粋に数学的なSU(2)ゲージ理論だと考えると、（１）式、（２）式、（３）式に問題はありません。各パウリ行列はそのゲージ変換の元で変化しますから、ゲージ不変量ではないのです。ゲージ理論の観測可能な物理量はゲージ不変であるべきなので、パウリ行列の物理量は観測されないことになります。ゲージに依存したパウリ行列が（１）式、（２）式のようにクライン壷空間で２価的に変化しようと、観測されないのですから何も矛盾はないのです。

しかし気を付けなければならないことが残ります。ゲージ理論では各パウリ行列は観測可能ではなくなるのですから、そのゲージ理論での量子状態のトモグラフィに、そのパウリ行列の期待値は出てこないという点です。他のゲージ不変な観測量の確率分布やその期待値で、その理論の量子状態は決定されるのです。この点には十分な注意が必要です。

まとめると、私の教科書で扱われる「確率分布」に基づいた定式化では、その表記として密度行列および特別な場合としての状態ベクトルの２つが出てきますが、その２つの差は飽くまで見かけだけだということです。純粋状態にある量子系の物理現象は、そのどちらでも漏れなく記述することが可能です。ただし密度行列で扱われる混合状態については、下記の記事にある注意は必要となります。量子力学では、混合状態にも古典統計力学にはなかった性質が現れるのです。