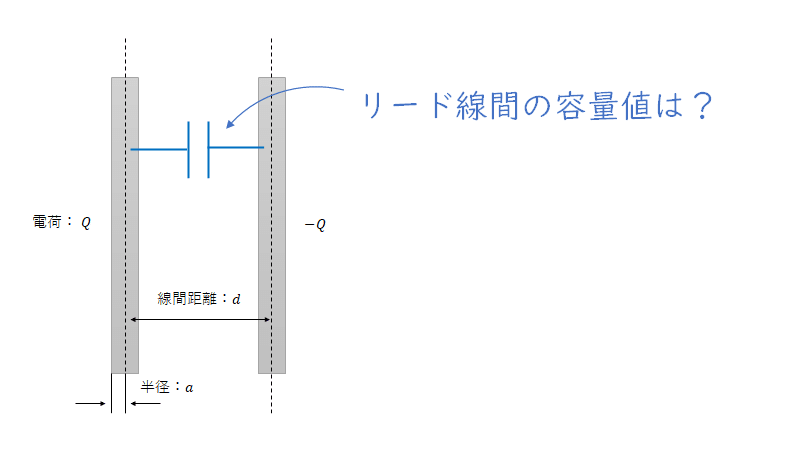
半径が$${a \text{ [mm]}}$$のリード線が線間距離$${d \text{ [mm]}}$$離れて平行しているとき、単位長さあたりの容量値$${C\ \text{[F/m]}}$$は以下の式となります。

$$
C=\frac{\pi \epsilon_{0}}{\ln{\frac{d-a}{a}}} \quad \text{[F/m]}
$$

無限長導線間の容量値の算出方法は多くの大学の電磁気学の教科書に記述されているかと思いますが、EMCのカップリングノイズを考える上で基本となる重要なパラメータですので、その導出方法を本稿に記載します。

導出方法

無限長平行導線間の容量値はガウスの法則を用いて簡単に導出することができる。その導出の流れとしては以下の通り。

1. 平行する無限長導線に電荷がそれぞれ単位長さあたり$${\pm Q \text{ [C/m]}}$$に帯電していると考えた時、単位長さの導体による電場$${\bm E}$$を算出する。

2. 電場$${\bm E}$$から導線間の電位差$${V}$$を算出する。

3. 公式$${Q=CV}$$より、単位長さあたりの静電容量$${C \text{ [F/ m]}}$$が算出される。

Step1 無限長導線の電場

ガウスの法則は電場と電荷の関係を表す公式で、以下の式で表される。

$$
\oint_S \bm{E} \cdot \bm{n} dS=\frac{Q}{\epsilon_{0}}
$$

ガウスの法則の意味は、以下の通り。

この"垂直に"というところに注目して、以下のような軸が導線と同一の半径$${r \text{ [m]}}$$, 高さ$${1 \text{ [m]}}$$の円柱形の閉曲面を考える。

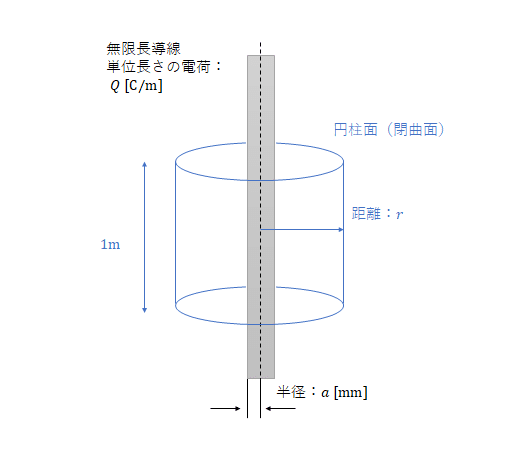
導線が無限長に伸びており、電荷が一様に分布していることから、閉曲面の底面を垂直に貫く電場の成分は打ち消し合い、$${0}$$となる。
したがって側面を垂直に貫く電場のみを考えれば良く、閉曲面の側面の面積が$${2 \pi r}$$, 閉曲面内に存在する電荷量は$${Q \text{ [C]}}$$であることから、導線から距離$${r}$$における電場$${E_{r}}$$は以下の式となる。

$$
E_{r}=\frac{Q}{2\pi\epsilon_{0}r}
$$

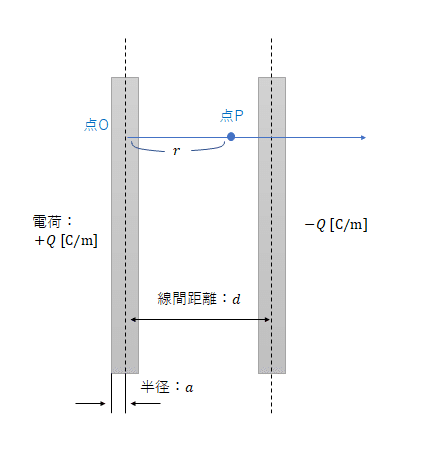
次に下図のように、それぞれ単位長さあたりの電荷$${\pm Q [C/m]}$$に帯電する平行導線に関して、正に帯電する導線から距離rにおける電界を考える。
正電荷$${+Q}$$に帯電する導線による電界を$${E_{r+}}$$, 負電荷$${-Q}$$に帯電する導線による電界を$${E_{r-}}$$とおくと、点$${P}$$における電界はそれぞれ以下の式の通りとなる。

$$
\begin{align*}
E_{r+}&=\frac{Q}{2\pi\epsilon_{0}r} \\ \quad \\
E_{r-}&=\frac{Q}{2\pi\epsilon_{0}(d-r)}
\end{align*}
$$

電場の向きはどちらも$${+ \bm e_r}$$方向である。
したがって、点$${P}$$における合成の電場は以下の式の通り。

$$
E_{r}=\frac{Q}{2\pi\epsilon_{0}}(\frac{1}{r}+\frac{1}{d-r})
$$

Step2 電位差の計算方法

電位は$${+1\text C}$$の電荷を無限遠点からその位置までに移動させるのに必要な仕事量である。電位の公式は以下の式で与えられる。

$$
\phi=\int_\infin^a -\bm{E(r)} \cdot d\bm r
$$

したがって、2線間の電位差は以下の式となる。

$$
\begin{align*}
V&=\int_\infin^a -\bm{E(r)} \cdot d\bm r - \int_\infin^{d-a} -\bm{E(r)} \cdot d\bm r \\ \quad \\
&=\frac{Q}{2 \pi \epsilon_0} \int_a^{d-a}(\frac{1}{r}+\frac{1}{d-r}) \\ \quad \\ 
&=\frac{Q}{2 \pi \epsilon_0} \{ [\ln r]_a^{d-a}-[\ln d-r]_a^{d-a} \} \\ \quad \\
&=\frac{Q}{ \pi \epsilon_0}\ln\frac{d-a}{a}
\end{align*}
$$

Step3 静電容量の導出

公式$${Q=CV}$$より、単位長さ$${(1\text m)}$$あたりの静電容量は以下の式となる。

$$
C=\frac{ \pi \epsilon_0}{\ln\frac{d-a}{a}} \quad \text{[F/m]}
$$

また、$${d>>a}$$の時は以下の式の通り近似される。

$$
C=\frac{ \pi \epsilon_0}{\ln\frac{d}{a}}\quad \text{[F/m]}
$$

ちなみに真空の誘電率は、光速と透磁率を暗記していれば導出できる。

$$
c=3.0 \times 10^8, \quad \mu_0=4 \pi \times 10^{-7} \\ \quad \\
c=\frac{1}{\sqrt{\epsilon_{0} \mu_{0}}} \\ \quad \\
\rightarrow \quad \epsilon_{0}=\frac{1}{120\pi} \times 10^{-9}=8.84 \times 10^{-12} \quad \text{[F/m]}
$$

また、真空の特性インピーダンスから計算しても、誘電率は同じ値となる。

$$
Z_0=\sqrt{\frac{\mu_0}{\epsilon_0}} =120 \pi \ [\Omega]
$$

まとめ

以上で、リード線間の容量値が以下の式となることを導出できた。

$$
C=\frac{\pi \epsilon_{0}}{\ln{\frac{d-a}{a}}} \quad \text{[F/m]}
$$

最後に、実際の容量値を計算してみよう。
長さ$${30\text{cm}}$$, 直径$${1\text {mm}}$$, 導線間距離を$${1.5\text{mm}}$$から離していったときの容量値は以下のように推移する。

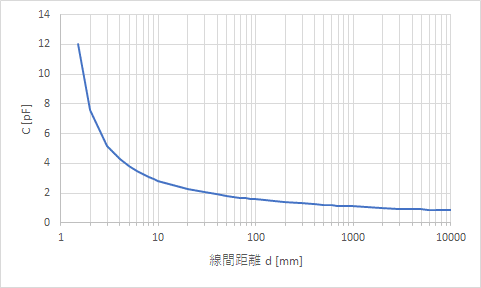
上のグラフから分かるように、当然だが、リード線間が離れるにつれ容量値は小さくなる。
この[pF]の容量値がどのように効いてくるのかについては別の記事にまとめる。