本稿では、平行2線式線路の特性インピーダンスの式とその導出方法を紹介する。

特性インピーダンスの式

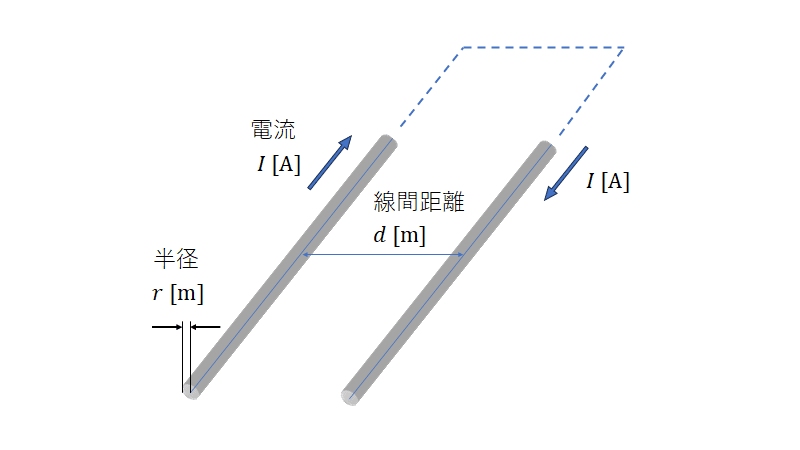
平行2線式線路の特性インピーダンス$${Z_0}$$は次式である。

$$
Z_0 =\frac{1}{\pi}\sqrt{\frac{\mu_0}{\epsilon_0}}\ln{\frac{d-r}{r}} \quad [\Omega]
$$

ただし、$${r}$$はリード線の半径、$${d}$$は線間距離である。
また、$${\sqrt{\mu_0/\epsilon_0}}$$は真空のインピーダンスで$${120 \pi \ [\Omega]}$$に近似でき、線路の周りの媒質（誘電体）の比誘電率$${\epsilon_r}$$を考慮すると、次式となる。

$$
Z_0=\frac{120}{\sqrt{\epsilon_r}}\ln\frac{d-r}{r} \quad [\Omega]
$$

特性インピーダンスとは？

特性インピーダンスを導出するために、そもそも特性インピーダンスとは何か？その定義を考える。

特性インピーダンスの定義は以下の通り。

特性インピーダンスは、分布定数回路における伝送線路の特性を表す。

一様な伝送線路を無限に伸ばしたとき、その線路上おいて、どの点でも電流と電圧の比$${Z_0}$$は同じとなる。この$${Z_0}$$のことをその線路の特性インピーダンスという。

この概念を理解する為には、分布定数回路をまず理解する必要がある。
分布定数回路の定義を以下に示す。

平行2線式線路においても、信号が高周波の時、もしくは波長に対し線路長が長い時に、分布定数回路として考える必要がある。

平行2線式線路は導線が平行している構造から、導線間にはキャパシタンスが発生し、マクロ的に見れば1巻きコイルの構造となっていることからインダクタンスを有し、さらに導体には抵抗があるため抵抗成分もある。それらの各素子成分が導線上に連続的に分布して存在している。

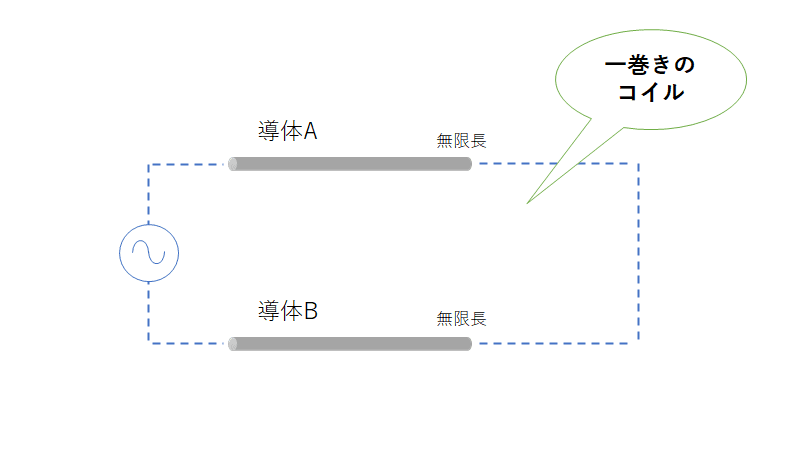
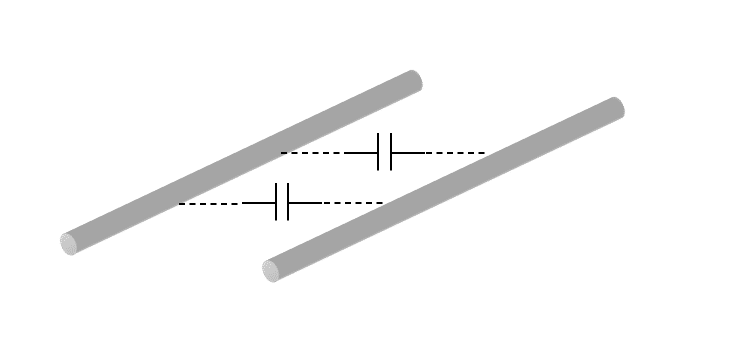
したがって、導線上では連続的に電圧降下や漏れ電流の発生による電流の分岐が発生する。電気回路を、連続的かつ無限に回路素子が分布している回路モデルで扱う考え方を分布定数回路という。

ここで、伝送線路上の微小な部分を取り出して考える。微小距離部分には先述の微小素子$${L, C, R}$$の組み合わせで表現される。

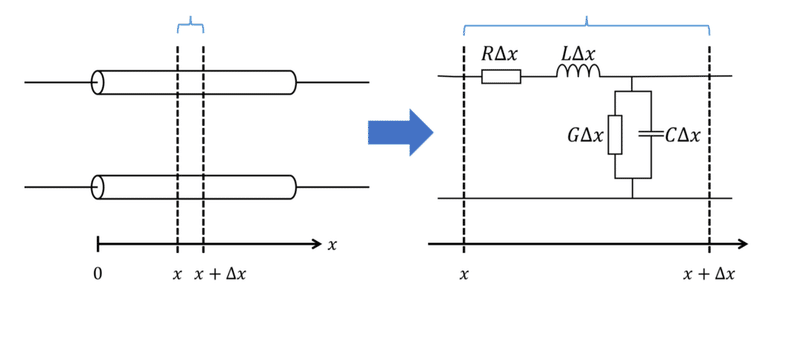
線路上のある地点$${x}$$から微小距離区間$${x+\Delta x}$$に着目したときの等価回路は下図となる。分布定数回路における素子値は、下記のように単位長さ当たりの値が定義されている。

$$
\begin{align*}
&R \ [\Omega/\text{m}] : 単位長さ当たりの抵抗値 \\
&L \ [\text{H/m}] : 単位長さ当たりのインダクタンス \\
&G \ [\text{S/m}] : 単位長さ当たりのコンダクタンス\\
&C \ [\text{F/m}] : 単位長さ当たりのキャパシタンス
\end{align*}
$$

すなわち、$${\Delta x}$$の微小区間において、抵抗、インダクタンス、コンダクタンス、キャパシタンスは、それぞれ$${R\Delta x}$$, $${L\Delta x}$$, $${G\Delta x}$$, $${C\Delta x}$$となる。

特性インピーダンスが電圧と電流の比であることを先述した。
以降で、分布定数回路の電圧と電流の式について考えていく。

微小区間における電圧と電流の変化量は次式の通り表される。

$$
v(x)-v(x+\Delta x) = R\Delta x\cdot i(x)+L\Delta x \cdot \frac{\partial i(x, t)}{\partial t} \\ \ \\
i(x) - i(x + \Delta x) = G\Delta x\cdot v(x)+C\Delta x \cdot \frac{\partial v(x, t)}{\partial t}
$$

上式について、$${v(x+\Delta x)}$$および$${i(x+\Delta x)}$$を$${\Delta x}$$でテイラー展開し、その1次の項までをとると次式が導出される。
これを分布定数回路の基礎方程式という。

$$
-\frac{\partial v}{\partial x} = Ri+L\frac{\partial i}{\partial t} \\ \ \\
-\frac{\partial i}{\partial x} = Gv+C\frac{\partial v}{\partial t} \\ \ \\
$$

上式をフェーザ表示すると、次式の通り表される。
これを伝送線路方程式という。

$$
\frac{d\bm{V}(x)}{dx}=-\bm{ZI}(x), \frac{d\bm{I}(x)}{dx}=-\bm{YV}(x) \\ \ \\
ただし、\bm{Z}=R+j\omega L, \bm{Y}=G+j\omega C
$$

これを$${x}$$についてもう一度微分し、それぞれを代入し変形すると次式が導出される。下式は波動方程式である。また、$${\gamma}$$は伝搬定数という。

$$
\frac{d^2\bm{V}(x)}{dx^2}=\gamma^2\bm{V}(x), \quad \frac{d^2\bm{I}(x)}{dx^2}=\gamma^2\bm{I}(x) \\ \ \\
ただし、\gamma=\sqrt{\bm{ZY}}
$$

この波動方程式の一般解は、次式となる。

$$
\begin{align*}
&\bm{V}(x)=Ae^{-\gamma x}+Be^{\gamma x} \\ \ \\
&\bm{I}(x)=\frac{1}{Z_0} \left( Ae^{-\gamma x}-Be^{\gamma x} \right)　\\ \ \\
&ただし、Z_0=\sqrt{\frac{\bm{Z}}{\bm{Y}}}=\sqrt{\frac{R+j\omega L}{G+j \omega C}}
\end{align*}
$$

上式の$${Z_0}$$を伝送線路の特性インピーダンスという。

電流と電圧の波動方程式の一般解の内、第1項は$${x}$$軸の正の向きに進む進行波、第2項は負の向きに進む反射波である。電圧と電流の進行波の比と反射波の比は、時間$${t}$$と場所$${x}$$によらず、常に$${Z_0}$$となる。

上記より、特性インピーダンスは伝送線路上における電圧と電流の比であることが分かる。

特に、線路が無損失（抵抗成分を無視できる）と考えると、特性インピーダンスは次式となる。

$$
Z_0=\sqrt{\frac{L}{C}} \quad [\Omega]
$$

導出方法

特性インピーダンスは、線路が無損失の場合、以下の式で表されることが分かった。

$$
Z_0=\sqrt{\frac{L}{C}} \quad [\Omega] \\ \ \\
ただし、L \ [\text{H/m}], C \ [\text{F/m}]
$$

つまり、特性インピーダンスは、単位長さ当たりのキャパシタンス$${C \ [\text{F/m}]}$$とインダクタンス$${L \ [\text{H/m}]}$$から導出される。

したがって、平行2線式線路のキャパシタンスとインダクタンスを電磁気学的に求めることで、特性インピーダンスが導出される。

以降で、それぞれの導出方法を紹介する。

単位長さ当たりのキャパシタンス

単位長さ当たりのキャパシタンスの式の導出は下記記事をご参照のこと。

単位長さ当たりのキャパシタンスは、次式の通り導出される。

$$
C=\frac{\pi\epsilon_0}{\ln{\frac{d-r}{r}}} \quad [\text{F/m}]
$$

単位長さ当たりのインダクタンス

単位長さ当たりのインダクタンスの式の導出は下記記事をご参照のこと。

単位長さ当たりのキャパシタンスは、次式の通り導出される。

$$
L=\frac{\mu_0}{\pi}\ln{\frac{d-r}{r}} \quad [\text{H/m}]
$$

特性インピーダンスの導出

単位長さ当たりのキャパシタンスとインダクタンスの式より、特性インピーダンスは次式となる。

$$
\begin{align*}
Z_0 &=\sqrt{\frac{L}{C}} \\ \ \\
&=\frac{1}{\pi}\sqrt{\frac{\mu_0}{\epsilon_0}}\ln{\frac{d-r}{r}} \quad [\Omega]
\end{align*}
$$

上式の$${\sqrt{\mu_0/\epsilon_0}}$$は真空の特性インピーダンスであり、その値は次式の通り近似される。

$$
\sqrt{\frac{\mu_0}{\epsilon_0}} \approx120\pi
$$

また、媒質の比誘電率が$${\epsilon_r}$$であるとき、誘電率$${\epsilon}$$は真空の誘電率$${\epsilon_0}$$を用いて、次式となる。

$$
\epsilon = \epsilon_r \epsilon_0
$$

したがって、媒質の比誘電率$${\epsilon_r}$$を考慮した式にすると、平行2線式線路の特性インピーダンスは次式となる。

$$
Z_0=\frac{120}{\sqrt{\epsilon_r}}\ln\frac{d-r}{r} \quad [\Omega]
$$

さらに、線間距離$${d}$$が導線半径$${r}$$より十分に長い時、次式の通り近似できる。

$$
Z_0 \simeq \frac{120}{\sqrt{\epsilon_r}}\ln\frac{d}{r} \quad [\Omega]
$$

参考文献

https://www2-kawakami.ct.osakafu-u.ac.jp/omu-content/uploads/sites/1161/Lecture_Data/Electric_Circuit_II/01_Lecture/10_lecture_electric_circuit_II.pdf

例題と演習で学ぶ （続）電気回路 第12章　服藤憲司 著