音律についての雑学です。具体的な歴史については簡単な説明にとどめ、ピタゴラス音律や平均律など、代表的な音律がなぜ必要とされ、どのような数学的な方法で作られたかなどについて、図表を交えて説明しています。

　この記事は、「かしこい音楽理論①シリーズ」の番外編にあたります。かしこい音楽理論①第３回までの話題から完全に逸れた余談となります。
第１回「音名」
第２回「度数」
第３回「クオリティ」
を読んでおけば深い理解に繋がるかもしれません。
　作曲の方法を身につけることに直接的に繋がるわけでもないのですが、雑学として覚えておけば、ふとした瞬間に役立つ気がしないでもないです。読まなくても死にません。

音楽の神話

　第3回「クオリティ」にてちょっとだけ触れましたが、完全5度や完全4度の関係は、よく混ざって響き合う関係です。実は、幹音もこれが元になって生まれたものなのです。

　実は、音楽というものは今に至る歴史の大半の部分で、自然から与えられ自然へ捧げるものとして発達してきました。
　自然数の１から物を数えていくところから数学を学びはじめるのと同じで、音楽は人が自然に綺麗と思える音から扱おうとするところが最初の１ステップです。

　言ってみれば音楽は神秘主義から始まった文化なので、音楽理論のことをオカルトだと批判する人はある意味ではかしこいです。もっとかしこい人は音楽のありのままの姿を確かめようとするでしょう。

響き合う法則

　ところで、日本の義務教育の中学１年生の理科の課程に、空の箱に一本の弦を張りわたらせた形の「モノコード」という器具を用いた実験をする授業があります。
　その授業にて、弦を弾いたときになる音の高さが、「弦の太さ」「弦の長さ」(それに加えて「弦の緩みかた(張り方)」や「弦の材質＝体積あたりの質量＝質量密度」)の積に反比例するということを学びます。

　音の高さというのは、振動する物体の時間あたりの振動数すなわち周波数が耳や肌を通して感じられるものです。そして弦の太さや長さの違いなどというのは、つまり物体の振動しにくさ(振動が伝わる遅さ)に関わっています。
　このことをかしこい人向けに説明するなら、

振動が伝わる遅さと周波数は反比例する
(振動が伝わる速さと周波数は比例する)

ということになります。そして実は、この法則の大元となる発見をしたのがピタゴラスさんでした。

　彼はある日、沢山の鍛冶職人がハンマーで金物を叩いて鍛えている音が綺麗に響き合っていることに気づきました。時を超えた現代でもそういうことがありますが、音楽を日々の何気ない営みの中に見つけちゃったのですね。
　そこから、「ちょうど自然数比の重さのハンマーで叩いて鳴った音はよく混ざって響き合う」ことを発見し、後に、重さに限らない色んな条件や要素の自然数比によってもそれが実現することを発見しました。モノコードは、それらを発見していく過程でピタゴラスさんが発明したものだそうです。

　実は、第3回で説明したperfectのインターバルは、その中で最も単純な自然数比の要素をもつ２つの物体が発する音の高さの関係に由来します。
　ここでは説明のために、振動しにくさの原因となる要素のうち質量だけを例にあげてみます。質量以外が全く同じ条件であるとすると、質量と周波数はしっかり反比例するので、質量の比の逆が周波数の比になります。
　ちなみに、これは鉄琴や木琴の鍵盤が大きい(体積が大きい➔質量が大きい)ほど低い音が鳴る原理でもあります。

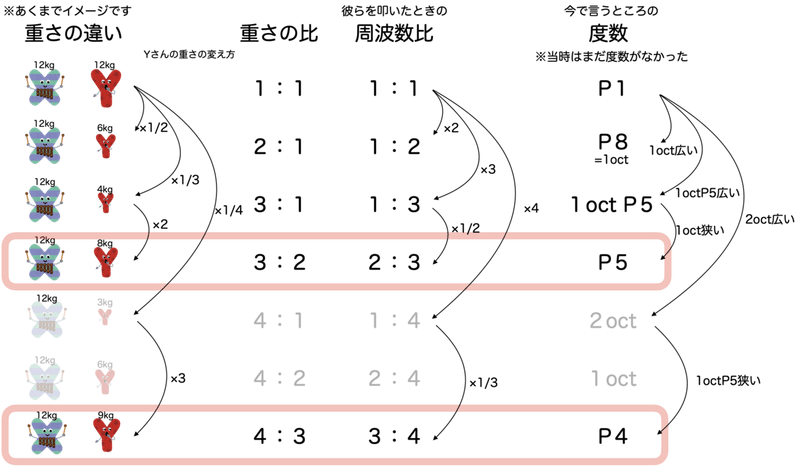
　天秤や物差しのような簡単な道具さえあれば、あまり細かい計量や計算をすることなしに2や3の倍数比の周波数を作り出せます。
　なかでも図中に枠をつけて示した周波数比(3/2倍や4/3倍)を掛け合わせることで、ただよく混ざって響き合うだけじゃない色んな響きのインターバルを作り出せることが分かりました。

　音楽がどんな文化圏においても親しまれるようになったのは、理屈さえ知っていれば誰にでも簡単によく混ざって響き合わせられる音たちを鳴らせる楽器が作れることがそもそもの根本にあります。
　もし仮に文明が滅んで技術が失われても、人類はこのことを思い出せさえすればまた新たに音楽を作れます。音楽理論というものは、もともとそういうものとして生まれてきました。やったね！

音律から音階へ

　基準となる音から、様々な条件によって他の音を定義していく(=律する)ことを音律といいます。
　先述したように、
「振動しにくさを2/3倍することで周波数比を3/2倍する操作」
「振動しにくさを3/4倍することで周波数比を4/3倍する操作」
　の２つを組み合わせるというのが世界最初の、原始的な音律の方法になりました。これをピタゴラス音律といいます。
　それ以前にも音の高さを感覚的に調整するいろいろな方法はあったようですが、ちゃんとした割合や数値などを用いて定義されるようになったのは歴史的にはピタゴラス音律が最初でした。厳密には、古代中国によるものが最初でしたが、これはピタゴラス音律とほぼほぼ同じ音律です。

　そして、なんらかの音律によって得られた音を、元の音の高さからみて2倍以内（＝オクターブ以内）になるようにまとめ、さらに低い方または高い方からの順番で並べた結果としてスケール(音階)が生まれたのでした。

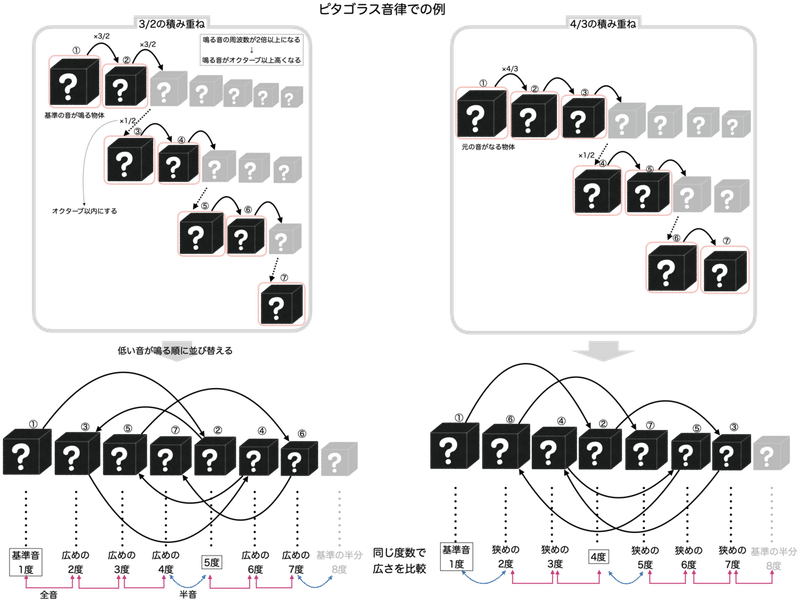
　音階の順番に沿って音を数えたり音同士の距離を測ろうとした結果として、今で言うところのインターバルという概念が生まれます。
　同じ度数のなかで狭いものがあったり広いものがあったりすることは、かなり曖昧な感覚として捉えられていました。それがやがてスケール同士の関係を第3回で説明したクオリティの概念、すなわちmajor/minor/augmented/diminishedへと具体化されていくことになります。

　2度や3度と同じように狭いものと広いものがあるのにも関わらず4度と5度がperfectというクオリティを持つ理由は、ある音を基準として音を定義すること＝音律で最も基本的なインターバルだからということなのです。

定音楽器の問題

　こうして音律によって定められるそれぞれの高さの音を鳴らす物体・あるいは構造を並べてできた楽器のことを、定音楽器と呼びます。木琴や鉄琴、ハープなどといった楽器や、あとはオルガンを始めとする鍵盤楽器、琵琶やギターをはじめとするフレット付きの弦楽器や木管楽器など、さまざまなものがこれに当たります。
　定音楽器ではないものとして、演奏者が自分の鳴らす音の高さを発音ごとに微妙にコントロールできる作音楽器があります。歌う人の声(ボーカル)や口笛なんかを楽器とするならばもちろん作音楽器に含まれるし、あとはトロンボーンやトランペットといった金管楽器、中国の楽器の二胡や三味線、ヴィオラやバイオリンなどをはじめとするフレットのない弦楽器などのようなものもこれに含まれます。

　ピタゴラス音律の仕組みで作っていた定音楽器では、複雑で高度な音楽を綺麗に作り上げていくことは非常に困難でした。2や3の倍数比を掛け合わせすぎることによって、非常に汚らしく響き合う音と音の組み合わせが生まれてしまうという限界があったのです。

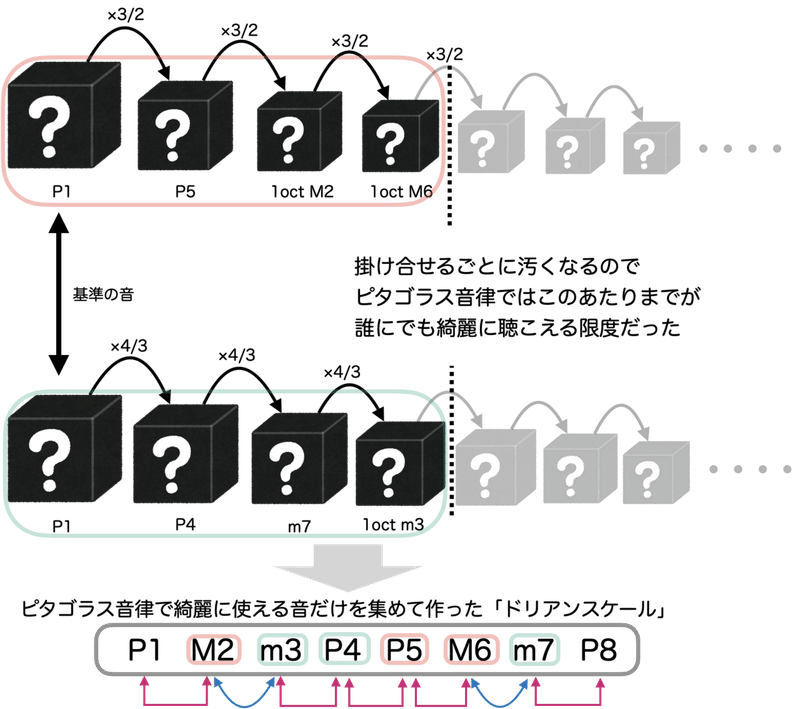
　とはいえあくまでそれはピタゴラス音律をきっちりと守る場合の問題であって、ピタゴラス音律だけでは定義しきれないような様々な音を、経験則や感覚を頼りに、微調整を行いながら使っていたらしいです。

純正律

　ピタゴラスの発見の応用として最も最初に生み出された純正律では、基準音やそれまでに作った音と非常に汚らしく響き合ってしまうような2と3の倍数比が掛け合わされまくった音の代わりに、それと近似する5の倍数比も使って作った音を取り入れることで、作音楽器に出せる様々な音に定音楽器が対応できないという欠点を部分的に解消しました。
　たとえば、ピタゴラス音律で長3度は周波数比64:81ですが、純正律ではその代わりに周波数比4:5となる音が使われます。実際、この周波数比の関係になる2音は、ピタゴラス音律よりも純正律の方が綺麗に響き合うことが実際に確かめられます。

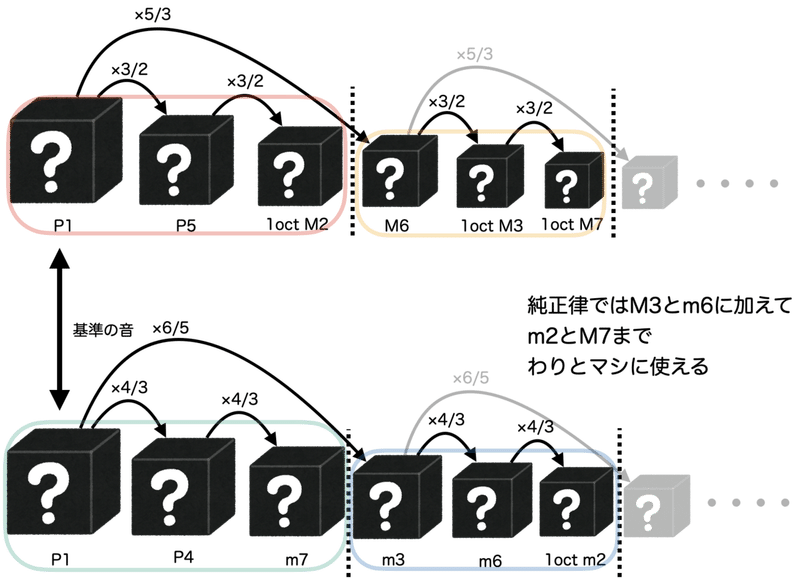
　ピタゴラス音律も純正律も自然数比のみを用いる以上、限られた掛け合わせ回数の音を使う分にはものすごく綺麗に響き合うことになります。
　しかし、掛け合わせた回数が多ければ多いほど基準の音とド汚く響き合う音が生まれちゃう欠点があったのでした。

　純正律に限った話として、他にも欠点はありました。それは5の倍数比を掛ける部分と全く掛けない部分があることが原因です。
　まず、同じ度数の周波数比に様々なバリエーションがあるといった欠点がありました。たとえば、m2・M2・M7・m7が基準の音ごとにバラバラで、スケールで上下に隣り合う音に動いていくメロディを作る上でチグハグさを感じさせてしまうことになりました。

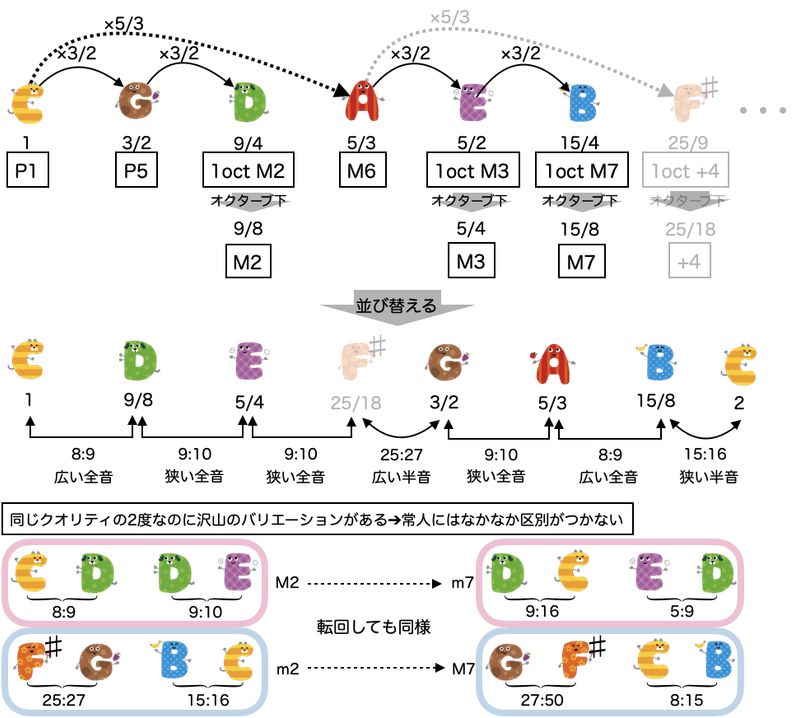
　また、元々の基準音から作った同じ音と別の基準音から作った同じ音が必ずしも一致しないという欠点がありました。全く同じ音程のスケールを用いたい場合は、基準の音を変えるたびに他の音を再度作り直さなくてはなりません。

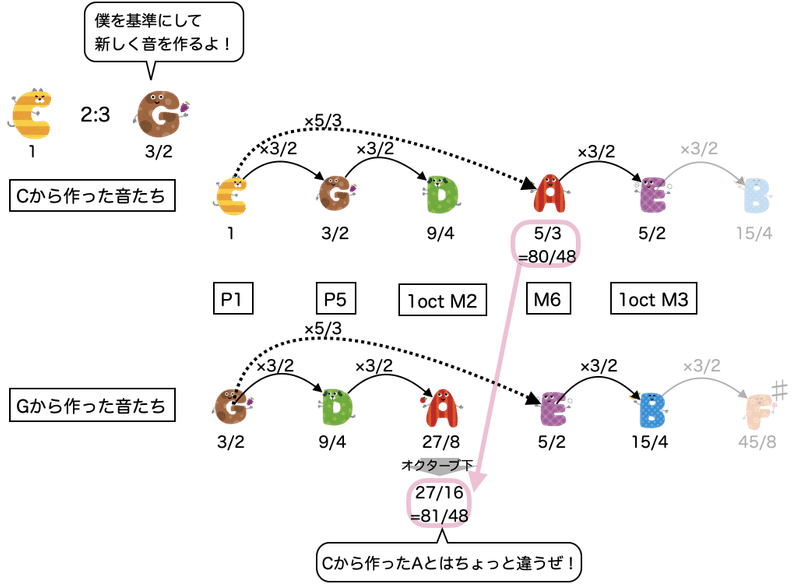
　これは発音ごとに音の高さを微調整できる作音楽器にとってはなんてことないことですが、一度作った音を基準とする音に合わせて調節しにくい定音楽器にとっては、中々に面倒な状況でした。

累乗根比の音律

　そこで、そういった問題を解決するために、掛け合わせの回数に応じて周期的に自然数比になり、なおかつあるインターバルのちょうど中間をとる累乗根比の音律が生まれてきました。

　主に作音楽器の分野では、あくまで経験則・感覚の上でですが、半音や全音が全て等しくなるように音の高さを調節していたようなのですが、それを確実に実現する実践的方法として、累乗根比の音律自体は、かなり古くから発明・発案されていました。
　しかし、累乗根比を実際の楽器の構造として精密に実現することにかなりの技術・知識レベルを必要とすることを主な背景として、限られたエリート層だけでなく楽器を扱う職人や技術者にまでそうした知識が広まって冪乗根比の音律が一般化するまでには、かなりの歳月を必要としました。

　インターバルは「掛け合わせて(乗算して)」作るものなので、インターバルを平均化するためには相乗平均を使うことになります。問題は、どのインターバルの平均を取るか、ということでした。

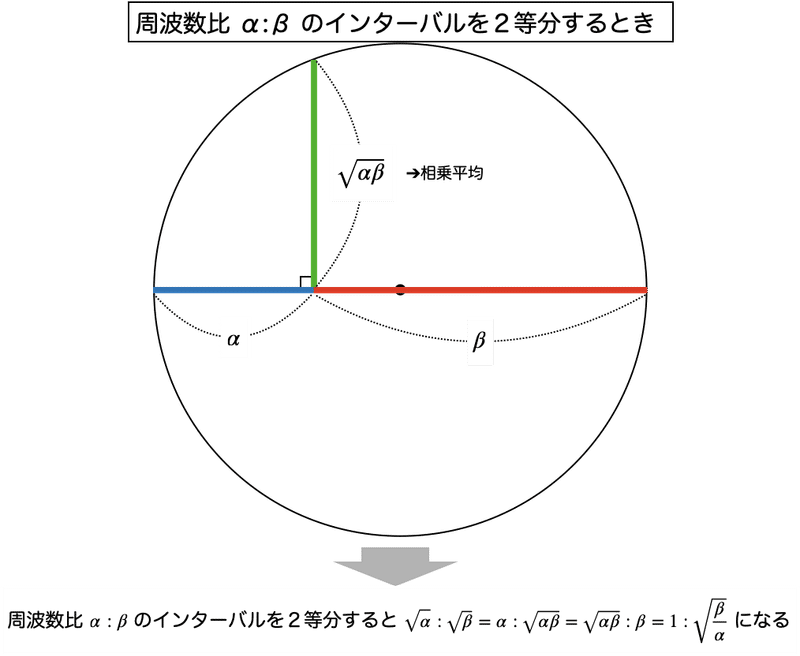
中全音律

　冪乗根比の音律の中で最も最初に世に広まったのは中全音律でした。
　これは純正律だけの問題となった8:9と9:10という2種類の全音の相乗平均すなわち中全音である2:√5を全音のインターバルとして定義するものです。　実は、このことは純正律の2octM3(1:5)を2等分して1octM2を1:√5と定義することも同時に意味します。

　また、もともとP5を2回掛け合わせて1oct M2が作られてきたことから、P5のインターバルも、中全音律における1oct M2(1:√5)を2等分した1:(5の4乗根)へと狭められる事になりました。

　数値にしてみれば元が2:3=1:1.5だったものが約1:1.49535となるもので、この差(約0.311%)は、単純な割合にしてみればピタゴラス音律におけるM3(81:64)と純正律および中全音律におけるM3(5:4=80:64)との差(1.25%)の1/4程度です。
　言い換えれば、この差を利用して、純正律と同じようにM3が綺麗に響き合い、なおかつ純正律よりも全音がバランス良く使えることを優先してP5とP4を新たに定義し直したものが中全音律であるともいえます。

異名同音程および異名同音

　音律によって定義できるのは、P1やP8(基準の音)と異名同音になる+7とo2までが限度とされます。なぜなら、それ以上積み重ねても既に作った音と同じような音しか作れなくなってしまい、音楽にとって意味のある音の高さの違いを得られなくなるためです。

　ここで音律ごとに+7からo2までがどのように作られるか、概略のイメージで確認してみましょう。

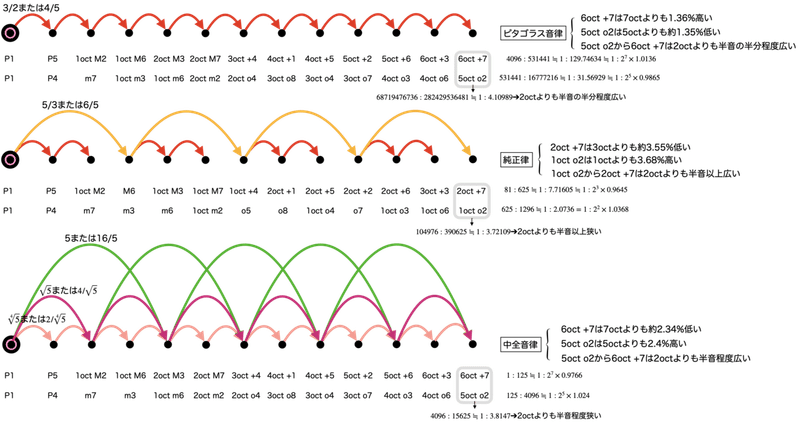
　　+7ないしo2に至るまでに、P5またはP4の12回の積み重ねがあります。異名同音程をなす音(異名同音)の組み合わせが各クオリティで２回以上現れることになります。実は、第３回で登場した半音数とクオリティの関係図は、まさにそのことを表しています。

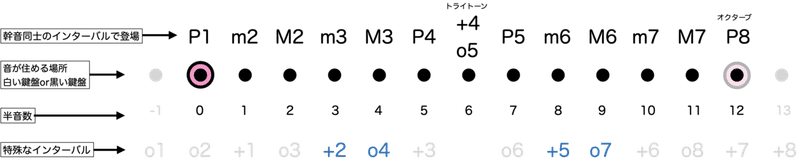
　上の図のように、ある音から作り出した音を１オクターブ内にまとめたものを半音階(Chromatic scale)といいます。

　ところで、P1とP8のo2と+7との厳密な広さの違いを比べてみると、異名同音程であっても細かな差異が生じていることがわかります。
　そして各音律の定義を考えれば、こうした差異はあらゆるクオリティにおいても大小の差はあれど全て現れていることもわかります。

　これらの音律における異名同音および異名同音程の微妙な違いを感じることは出来るし、その違いを音楽表現に用いることもできるのは確かなのです。
　しかし、それよりも問題だったのは、音の高さに対して柔軟に対応できる作音楽器と、それができない定音楽器との間に、音楽での用いられ方の大きな隔たりがあったことでした。実はこのことはアンサンブルに用いられる楽器の組み合わせに制限があることも意味します。
　細かい事情は省きますが、究極的には、「半音2コ分が全音に等しい」こと、そして「異名同音程の広さ・異名同音の高さが全て等しい」ことによってその問題は解決することができます。前者は例えば中全音律の全音を2等分すれば実現できますが、後者はそのままの方法だと実現できませんでした。

十二平均律

　6oct +7を7octに一致させ、また5oct o2を5octと一致させることで、理論上は全ての異名同音程が一致することになります。6oct +7はP5を12回分、5oct o2はP4を12回かけ合わせたものです。
　そこで、6oct +7=1:(2の7乗)を12等分したものをP5と定義し直し、5oct o2=1:(2の5乗)を12等分したものをP4として定義し直した音律のことを十二平均律といいます。

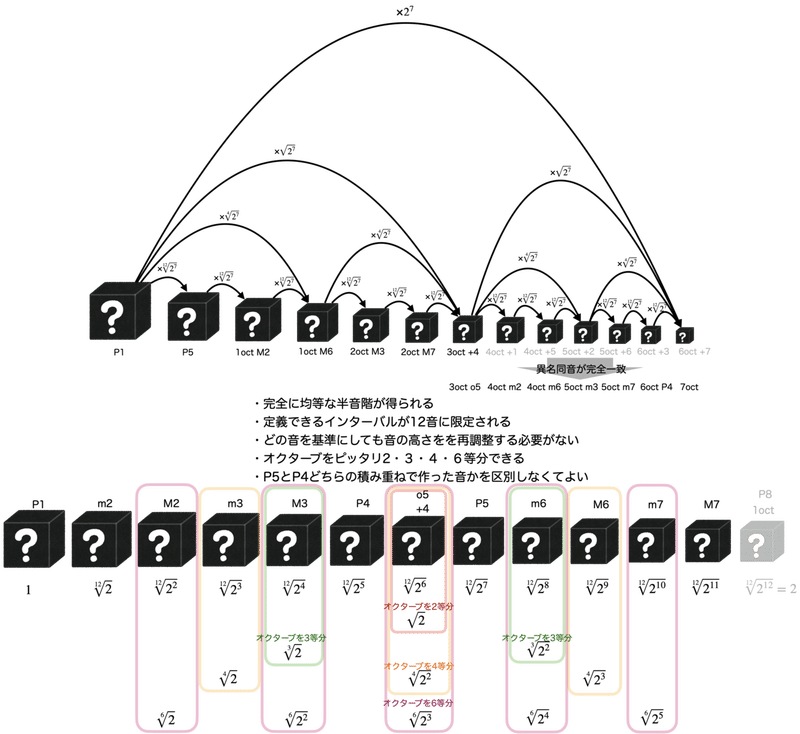
　十二平均律では、音律というものが生まれるそもそもの発端だったはずの単純な自然数比はもはやP1(1:1)とP8(1:2)でしか得ることはできません。
　しかしこれまで述べてきたように、十二平均律においては、作音楽器と定音楽器が全く同じ立場で活躍できるという最大の利点があったのでした。

　また、他の音律においては、異名同音程および異名同音の区別はそれなりに重要なものです。しかし、それを耳で聴いて区別するにはかなり高度な水準の音感が必要です。
　平均律では異名同音の区別が全く必要なくなることにより、言ってみれば個々人が音楽を実現するまでに鍛えなくてはならない音感のレベルが大幅に下がることになりました。

　ピタゴラス音律が発明されたことにより、音楽を実現できる可能性が飛躍的に高まる結果になりました。そして、十二平均律でもそれと同じようなことが起きたのですが、それは自然に与えられ自然に捧げるものとしての音楽としてではなく、より多くの人間が楽しむための音楽を実現できる可能性を高める方向に働いたのです。
　ポピュラー音楽のほぼ100％は平均律で作られています。

代表的な音律の比較

　さて、第3回で紹介した基本的な12のインターバルにて、各音律の違いを確認してみましょう。

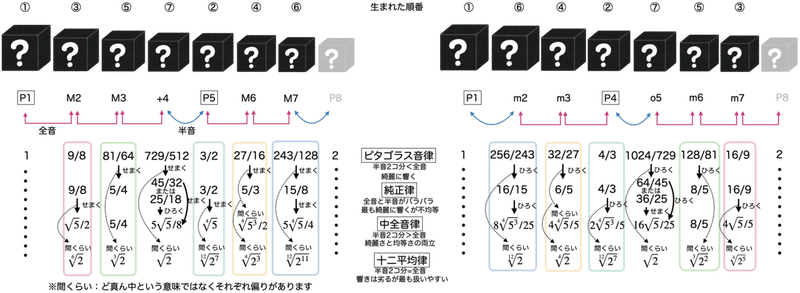
　各度数ごとにそれぞれ多種多様な差がありますが、十二平均律はおおむね純正律や中全音律よりもピタゴラス音律に近いことがわかります。
　その近さというのがどれくらいの距離感なのかも十二平均律を基準にして半音階の形式で示しておくことにします。

　ピタゴラス音律、純正律、中全音律、十二平均律は、あくまで今まで発明された音律の代表格で、実際には、これらの他に中全音律の微調整バージョン、純正律に7の倍数比を取り入れたもの、12等分よりもさらに多くに分割する別種の平均律など、色々なものが存在します。しかし、ここでは割愛することにしました。