📏「でたらめ」の数学 確率過程 ランダム関数 ウィーナー過程、ブラウン運動、マルコフ過程の違い
確率過程とはランダムに変化する数学モデル、とにかくデタラメになにか出てくる数が多めのもの
確率過程(stochastic process)は例えば、バクテリアの個体数の増加、熱雑音による電流の変動、気体分子の運動などである。 [さらに、金融市場における一見不規則な変化から、金融における確率過程の広範な利用が進められている
過程と言う言葉に惑わされてはいけない。関数程度に考えてあげて。≒ランダム関数
確率過程は関数空間におけるランダムな要素とも解釈できる。ランダム関数という用語は確率過程またはランダム過程を指す場合にも用いられる。
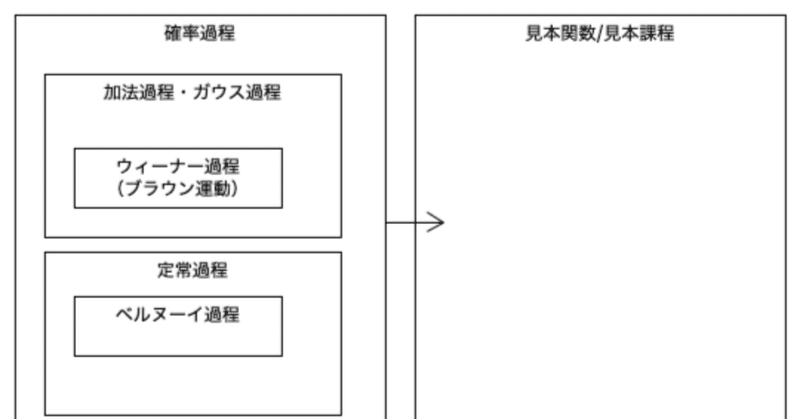
確率過程はその数学的性質から,ランダムウォーク、マルチン ゲール、マルコフ過程、レヴィ過程、ガウス過程 、ランダム場、 更新過程,分岐過程など様々なカテゴリーに分類され る
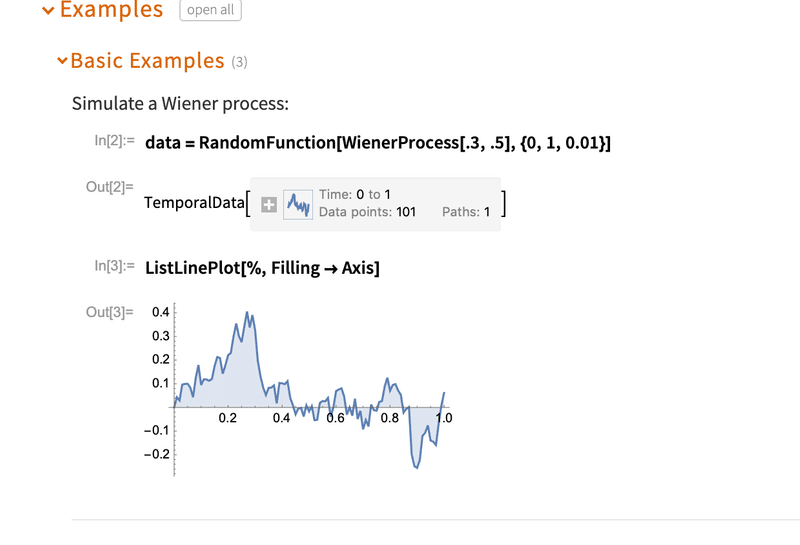
ウィーナー過程=ブラウン運動過程または単にブラウン運動とも呼ばれている ブラウン運動するランダムな関数。増分がポイント
ウィーナー過程は、定常的で独立な増分を持ち、増分の大きさによって正規分布する確率過程である。ウィーナー過程は、その数学的存在を証明したNorbert ウィーナーにちなんで名付けられたが、液体中のブラウン運動のモデルとして歴史的に関係があるので、ブラウン運動過程または単にブラウン運動とも呼ばれている。(ウィーナー過程=ブラウン運動過程)
ウィーナー過程は、数理科学のあらゆる分野に応用されている。物理学では、ブラウン運動、流体中に浮遊する微小粒子の拡散など、Fokker-Planck方程式やLangevin方程式による拡散の研究に用いられている。また、量子力学の厳密な経路積分定式化(Feynman-Kacの式により、シュレーディンガー方程式の解をWiener過程の観点から表すことができる)や物理宇宙論における永遠のインフレーションの研究の基礎を形成するものである。また、金融の数学的理論、特にブラック・ショールズ・オプション価格決定モデルにおいても著名である。

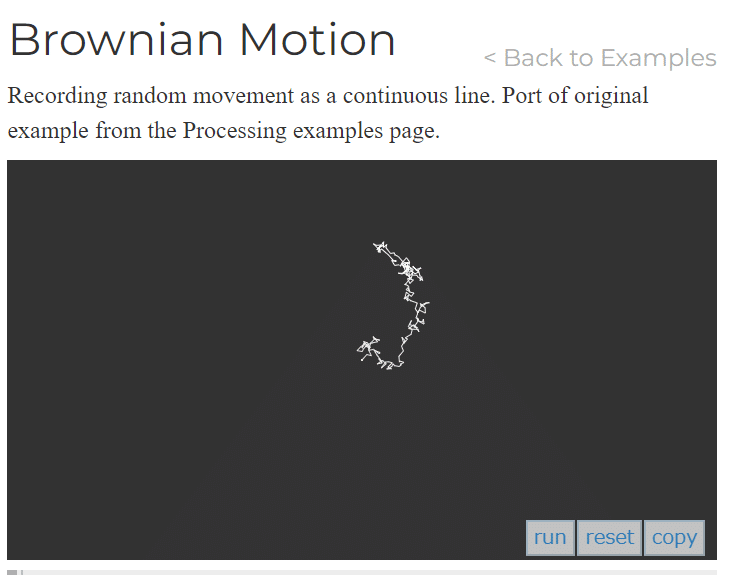
花粉は出鱈目(ランダム)に移動する、しかし瞬間移動することはない(なのでランダムに増・減するモデル)

常に現在の位置 (x または y) に追加されるため (これがコンテキストを維持するための鍵です)、どこにいてどこに行くべきかを常に意識することができます。
マルコフ過程
https://setosa.io/ev/markov-chains/
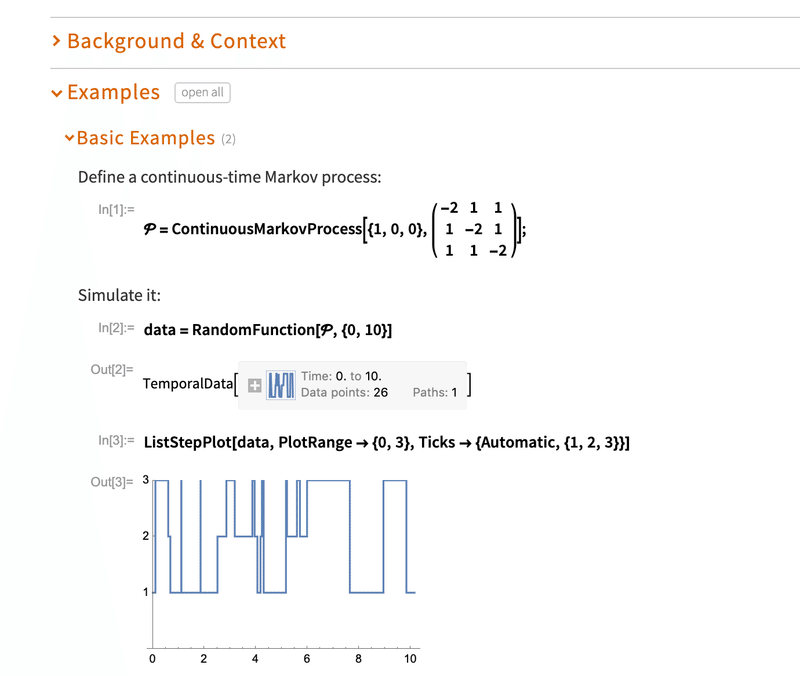
マルコフ過程は、伝統的に離散時間または連続時間の確率過程(ランダム関数)であり、マルコフ特性を持つ。これは、マルコフ過程の次の値は現在の値に依存するが、確率過程の以前の値からは条件付きで独立であることを意味する。言い換えれば、プロセスの現在の状態が与えられれば、そのプロセスの将来における振る舞いは、過去における振る舞いから確率的に独立である
マルコフ連鎖は通常、状態遷移図によって示される。
ブラウン運動も近似的にはマルコフ性を有する。
水中のブラウン 運動では,水由来の流体力学 相互作用に起因して,強い非マルコフ性を示す
https://www.jps.or.jp/books/gakkaishi/2021/06/76-06_360researches3.pdf
どっちやねん。。。。
確率過程はランダムな現象であるので法則性は観測者にゆだねられる
じゃんけんの現在の戦況から次の手を選べばマルコフ性(現在が未来を決めてる)を有するし、過去10回の結果から結果を出す性質があれば非マルコフ性(過去が関与している)を有する事になる。
観測者や実施者の匙加減で、現象のマルコフ性は変わっていく。(恣意的な感じがベイズにも繋がるはず)
しかし、多くのデジタル処理は離散的(配列、出目、などに制限がある。上下左右なども)であり、マルコフ性をあてはめやすい。
ずっとグーを出し続ければ「同じ手」であって、それをパーに変えた場合「グーからのパー」になる。状態遷移はじゃんけんのルールによって補償されている。
状態遷移で制限、出鱈目ときたら、マルコフ性のセットアップは可能
もちろん、非マルコフ的にみることも可能。将棋、チェス、囲碁、オセロ、などなど。。。。。
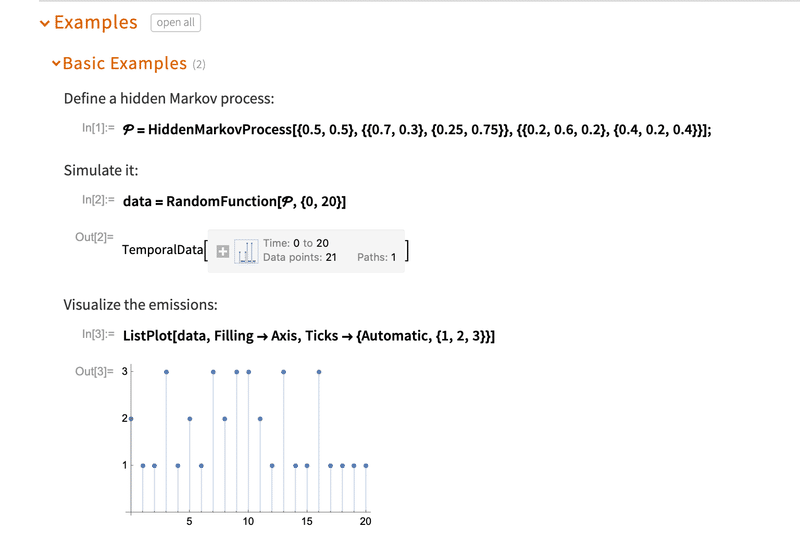
マルコフ過程は確率過程の重要なクラスを形成し、多くの分野で応用されている。例えば、マルコフ連鎖モンテカルロとして知られる一般的な確率シミュレーション手法の基礎であり、特定の確率分布を持つランダムな対象をシミュレーションするために用いられ、ベイズ統計で応用されてきた
マルコフ連鎖モンテカルロ法 (MCMC) では、均衡分布の近辺を小さなステップで無作為に動き回る粒子を想定したアルゴリズムが多い。これをランダムウォーク(酔歩)という。
ホークス過程(非マルコフ性をもつ)
非マルコフ型ダイナミクスとは、あるシステムとその環境との間のあらゆる相互作用のことで、その環境は後の時間にそのシステムに影響を与えるもので、コヒーレントである必要さえない。
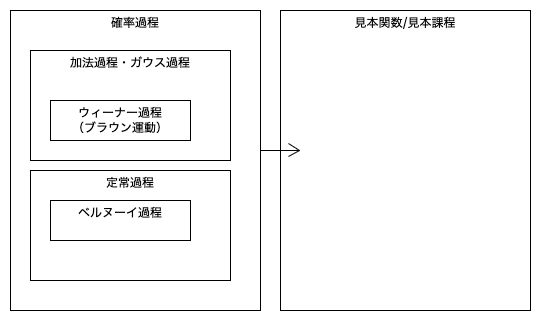
ランダムウォーク (Random Walk): これは、ランダムに一連のステップを取る過程です。例えば、コインを投げて、表が出れば一歩前進し、裏が出れば一歩後退するようなものです。この過程は、株価の動きや物理学における粒子の動きなどをモデル化するのに用いられます。
マルチンゲール (Martingale): これは、過去の情報に基づいて未来の価値を予想する際に、現在の価値が最善の予想であるとする過程です。ギャンブル(特に公正なゲーム)において、現在の持ち金が将来の予測値となります。
マルコフ過程 (Markov Process): この過程では、将来の状態は現在の状態にのみ依存し、過去の状態には依存しません(「無記憶性」)。例えば、天気のモデル化に使われることがあります。
レヴィ過程 (Lévy Process): これは、マルコフ過程の一種で、独立した増加と定常的な増加を持つ過程です。ブラウン運動やポアソン過程などが含まれます。
ガウス過程 (Gaussian Process): これは、連続するランダム変数の集合で、任意の有限集合が多変量正規分布に従う過程です。機械学習、特に回帰問題で用いられます。
ランダム場 (Random Field): 空間の各点にランダムな値を割り当てる過程です。例えば、気温や圧力の分布をモデル化するのに使われます。
更新過程 (Renewal Process): 一連のイベントが発生する時間間隔が独立している過程です。これは、機械の故障や修理のモデリングに用いられることがあります。
分岐過程 (Branching Process): それぞれの世代で個体がランダムに子孫を生む過程です。これは、生物学における個体群の成長や核分裂のモデル化に使われます。
お願い致します
