背景

Aidemyでデータ分析講座を受講し、成果物で回帰分析に挑戦した。昨今、環境問題が深刻になっていく中で、地球温暖化による日本近海の海面上昇に着目した。私が海に近い地域に住んでいることもあり、海に関するテーマを選んだ。

目的

目的変数である海面水位に対して、下記2点が説明能力を持つのかを検証することである。
以下の2点が海面上昇の原因だと言われている。
①氷河/氷床に貯蔵されていた氷の融解
②水温が高くなることによる海水体積の膨張
①については、日本に近いオホーツク海の海氷最大面積の推移データを扱う。②については、熱膨張等のデータが無かったため、全球に関する海洋貯熱量を利用した。海面上昇は日本沿岸の海面水位のデータを利用し、それぞれのデータは気象庁が発表しているデータを使用した。

本題

実行環境

• Google Colaboratory

• Python 3.10.12

1.データの加工、可視化を行う

1-1.それぞれのデータフレームの加工

各データは以下の気象庁のデータを使用した。(https://www.jma.go.jp/jma/menu/menureport.html)

 #1 .heat volume(海洋貯熱量)のデータ整形
import pandas as pd
df1=pd.read_table("/content/drive/My Drive/Colab Notebooks/heat volume.txt",delim_whitpace=True)

df1_1=df1.drop(range(0,16))
df1_1=df1_1.reset_index(drop=True)
df1_1=df1_1.rename(columns={'Year':'Year(heat_volume)'})
 #2 . sea ice ara(最大海氷域最面積)のデータ整形
df2=pd.read_table("/content/drive/My Drive/Colab Notebooks/sea ice area.txt")
df2_1=df2.rename(columns={'SEASON':'Year(sea_ice)'})
 #3 . sea level(海面水位)のデータ整形
df3=pd.read_excel("/content/drive/My Drive/Colab Notebooks/sea level.xlsx")

df3_1=df3.drop(range(0,11))
df3_1=df3_1.reset_index(drop=True)
df3_1=df3_1.rename(columns={'年': 'Year(sea_level)', 
                            '北海道・東北地方沿岸の偏差（mm）' : 'North (mm)',
                            '関東・東海地方沿岸の偏差（mm）':'East low',
                            '近畿〜九州地方の太平洋側沿岸の偏差（mm）':'South',
                            '北陸〜九州地方東シナ海側沿岸の偏差（mm）':'East high',
                            '4海域平均（mm）':'average'})

def show_many_heads(*dfs, n=6):
    class HorizontalDisplay:
        def _repr_html_(self):
            template = '<div style="float: left; padding: 10px;">{}</div>'
            return  ''.join(template.format(df.head(n)._repr_html_()) for df in dfs)
    return HorizontalDisplay()

show_many_heads(df1_1,df2_1, df3_1,n=6)

上記のデータ加工により、各データの年代を揃え、1971年から2022年の51年間を対象とした。df1_1は海洋貯熱量、df2_1は最大海氷域面積、df3_1は海面水位のデータである。以下に示す。

上記は左から順にdf1_1、df2_1、df3_1である。df1_1は年代と水深別で貯熱量の増加量を示している。今回は0-2000ｍを採用した。df2_1は年代とオホーツク海の海氷面積の最大値を示している。df3_1は年代と地方ごと(コードを参照)の海面水位の平年差を示している。

1-2.加工したデータを連結させ、回帰分析に必要な情報を抽出し、新たなデータフレームを作成する

df12=pd.concat([df1_1,df2_1],axis=1) #print (df12)
df123=pd.concat([df12,df3_1],axis=1) #print (df123)
df123_re=df123[['Year(heat_volume)','average','A(0-2000)', 'MAX (x10^4km^2)']]
df123_re=df123_re.rename(columns={'Year(heat_volume)':'Year','average':'sea_level','A(0-2000)':'heat_volume','MAX (x10^4km^2)':'sea_ice_area'}) #df123_re 

上記では、見やすいようにカラム名を変更している。

1-3. データを可視化する。

import matplotlib.pyplot as plt
import numpy as np
import plotly.express as px

a1=df123_re['Year']
b1_1=df123_re['heat_volume']
b2_1=df123_re['sea_ice_area']
b3_1=df123_re['sea_level']

fig1 = plt.figure(figsize=(18,4))
fig1.subplots_adjust(wspace=0.5, hspace=1)
ax1_1=fig1.add_subplot(1,3,1)
ax2_1=fig1.add_subplot(1,3,2)
ax3_1=fig1.add_subplot(1,3,3)

ax1_1.set_title('heat_volume_figure')
ax1_1.set_xlabel("year")
ax1_1.set_ylabel("heat_volume(×10^22J)")

ax2_1.set_title('sea_ice_area_figure')
ax2_1.set_xlabel("year")
ax2_1.set_ylabel("sea_ice_area(×10^4km^2)")

ax3_1.set_title('sea_level_figure')
ax3_1.set_xlabel("year")
ax3_1.set_ylabel("sea_level(mm)")

ax1_1.plot(a1,b1_1)
ax2_1.plot(a1,b2_1)
ax3_1.plot(a1,b3_1)
plt.show()

2. 重回帰分析

2-1. データを目的変数と説明変数に分ける

x = df123_re[['heat_volume', 'sea_ice_area']]
y = df123_re[['sea_level']]
x1_1 = df123_re[['heat_volume']]
x2_1 = df123_re[['sea_ice_area']] #fig  = px.scatter_3d(df123_re, x='heat_volume', y='sea_ice_area', z='sea_level') #fig .show()

2-2. 線形回帰モデルの作成

まずは、必要なライブラリをインポートする

from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from statsmodels.stats.outliers_influence import variance_inflation_factor
from sklearn.metrics import r2_score

実際に、モデルを作成する。また、各統計量を算出する。

train_X, test_X, train_y, test_y = train_test_split(x, y, test_size=0.3, random_state=42)
model_lr = LinearRegression()
model_lr.fit(train_X, train_y)
 #予測値 
train_y_pred=model_lr.predict(train_X)
test_y_pred=model_lr.predict(test_X) #偏回帰係数 
df_coef = pd.DataFrame(model_lr.coef_.reshape(1,2),index=['偏回帰係数'],columns=[['heat_volume', 'sea_ice_area']])
display(df_coef) #定数項 
print('定数項')
print(model_lr.intercept_)
print('')
print('決定係数')
print('訓練データ:',model_lr.score(train_X, train_y))
print('テストデータ:',model_lr.score(test_X, test_y))
print('')
print('自由度調整済み決定係数') #自由度調整済み決定係数 
def adjusted_r2_score(y_actual, y_pred, number_dimensions):
    # 決定係数
    coefficient_of_determination = r2_score(y_actual, y_pred)
    # サンプルサイズ
    sample_size = len(y_actual)

    return 1 - (1 - coefficient_of_determination) * (sample_size - 1) / (sample_size - number_dimensions - 1)

# 訓練データ
print('訓練データ',adjusted_r2_score(train_y, train_y_pred, train_X.shape[1]))
# テストデータ
print('テストデータ:',adjusted_r2_score(test_y, test_y_pred, test_X.shape[1]))

2-3. 回帰直線を3次元上で示す

視覚的にわかりやすくするため、回帰直線をグラフで示す。

fig=plt.figure()
ax =fig.add_subplot(projection="3d")
ax.scatter(x1_1,x2_1,y)
ax.set_xlabel("heat_volume")
ax.set_ylabel("sea_ice_area")
ax.set_zlabel("sea_level")

mesh_x1 = np.arange(x1_1.min()[0], x1_1.max()[0], (x1_1.max()[0]-x1_1.min()[0])/20)
mesh_x2 = np.arange(x2_1.min()[0], x2_1.max()[0], (x2_1.max()[0]-x2_1.min()[0])/20)
mesh_x1, mesh_x2 = np.meshgrid(mesh_x1, mesh_x2)
mesh_y = model_lr.coef_[0][0] * mesh_x1 + model_lr.coef_[0][1] * mesh_x2 + model_lr.intercept_[0]
ax.plot_wireframe(mesh_x1, mesh_x2, mesh_y)
plt.show()

Figure2の網掛けの部分が回帰直線式を表している。

2-4. VIF値の算出

また、多重共線性の問題を確認する。今回はVIF値を算出することで確かめる。

from statsmodels.tools.tools import add_constant
def create_vif_df(c):
    c=add_constant(c)
    df_vif=pd.DataFrame()
    df_vif['features']=c.columns
    df_vif['VIF Factor']=[variance_inflation_factor(c.values, i) for i in range(c.shape[1])]
    return df_vif
vif_bef=create_vif_df(train_X)
vif_bef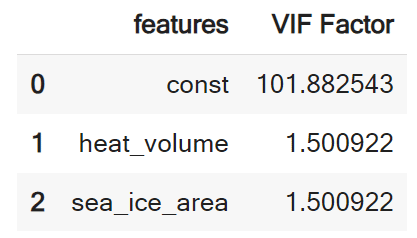

各説明変数のVIF値は1.5程度であることがわかる。

2-5. モデルの精度の確認

2-2で作成したモデルの回帰係数を確認すると、海洋貯熱量に関しては、係数が正になり一般的な理論と一致する。海氷域最大面積の係数は正の値となっているため、海氷面積が小さくなれば海面水位も下がるということになる。しかし、海面上昇の問題では、海氷面積が小さくなると海面水位が上がると言われている。よって、偏回帰変数は負の値になると考えることができる。一度、海洋貯熱量と海氷面積について、それぞれ海面水位に対する単回帰分析を行う。まずは、海洋貯熱量の単回帰分析を行う。

train_X_heat, test_X_heat, train_y_heat, test_y_heat = train_test_split(x1_1, y, test_size=0.3, random_state=42)
model_lr_heat = LinearRegression()
model_lr_heat.fit(train_X_heat, train_y_heat)
 #予測値 
train_y_pred_heat=model_lr_heat.predict(train_X_heat)
test_y_pred_heat=model_lr_heat.predict(test_X_heat) #偏回帰係数 
df_coef_heat = pd.DataFrame(model_lr_heat.coef_.reshape(1,1),index=['回帰係数'],columns=[['heat_volume']])
display(df_coef_heat) #定数項 
print('定数項')
print(model_lr_heat.intercept_)

次に海氷面積の単回帰分析を行う。

train_X_ice, test_X_ice, train_y_ice, test_y_ice = train_test_split(x2_1, y, test_size=0.3, random_state=42)
model_lr_ice = LinearRegression()
model_lr_ice.fit(train_X_ice, train_y_ice)
 #予測値 
train_y_pred_ice=model_lr_ice.predict(train_X_ice)
test_y_pred_ice=model_lr_ice.predict(test_X_ice) #偏回帰係数 
df_coef_ice = pd.DataFrame(model_lr_ice.coef_.reshape(1,1),index=['回帰係数'],columns=[['sea_ice_area']])
display(df_coef_ice) #定数項 
print('定数項')
print(model_lr_ice.intercept_)

単回帰分析の結果から海氷最大面積は予想通り、負の値になっているが重回帰分析では正の値になっていた。Table2の結果からVIF値は1.5ではあるものの多重共線性の影響があるのではないかと考えた。また、交絡変数の影響によって、偏回帰係数の正負が合わないという理由も考えた。そこで、この多重共線性を解決するために2通りの方法を考えた。
1通り目は海面水温が交絡変数だと仮定し、その影響を除く方法。
2通り目は主成分分析を行い、多重共線性を解決する方法。

3. 重回帰モデルの改善

まず、1通り目の交絡変数の影響を除く方法を記述していく。

3-1. 海面水温のデータを読み込み、加工する。

 #海面水温データをdf4とする 
df4=pd.read_table("/content/drive/My Drive/Colab Notebooks/sea temperature.txt",sep=',')
df4_1 = df4.drop(range(0,71))
df4_1.reset_index(drop=True,inplace=True)
df4_1.head(6)

3-2. データを連結させ、新たなデータフレームを作成する

df1234=pd.concat([df123_re,df4_1['Annual']],axis=1)
df1234['Annual']=df1234['Annual'].astype(float) #海面水温をsea_temperatureとする 
df1234=df1234.rename(columns={'Annual':'sea_temperature'})
df1234.head(6)

3-3. 1-3と同様にデータを可視化する。

a2=df1234['Year']
b1_2=df1234['heat_volume']
b2_2=df1234['sea_ice_area']
b3_2=df1234['sea_temperature']
b4_2=df1234['sea_level']

fig2 = plt.figure(figsize=(9, 9))
fig2.subplots_adjust(wspace=0.5, hspace=0.5)
ax1_2=fig2.add_subplot(2,2,1)
ax2_2=fig2.add_subplot(2,2,2)
ax3_2=fig2.add_subplot(2,2,3)
ax4_2=fig2.add_subplot(2,2,4)

ax1_2.set_title("heat_volume_figure")
ax1_2.set_xlabel("year")
ax1_2.set_ylabel("heat_volume(×10^22J)")

ax2_2.set_title("sea_ice_area_figure")
ax2_2.set_xlabel("year")
ax2_2.set_ylabel("sea_ice_area(×10^4km^2)")

ax3_2.set_title("sea_temperature_figure")
ax3_2.set_xlabel("year")
ax3_2.set_ylabel("sea_temperature(℃)")

ax4_2.set_title("sea_level_figure")
ax4_2.set_xlabel("year")
ax4_2.set_ylabel("sea_level(mm)")

ax1_2.plot(a2,b1_2)
ax2_2.plot(a2,b2_2)
ax3_2.plot(a2,b3_2)
ax4_2.plot(a2,b4_2)
plt.show()

figure3はfigure1にsea_tempereatureを追加したものになっている。

3-4. 目的変数と説明数に分ける

以下のように説明変数と目的変数に分ける。

x2 = df1234[['heat_volume', 'sea_ice_area','sea_temperature']]
y2 = df1234[['sea_level']]
x1_2 = df1234[['heat_volume']]
x2_2 = df1234[['sea_ice_area']]
x3_2=df1234[['sea_temperature']]

次に、説明変数を補正した変数に変える。方法としては、海洋貯熱量を海面水温で割った変数と海氷最大面積を海面水温で割った変数と交絡変数である海面水温の3つを説明変数として回帰分析を行う。理由については交絡変数であると仮定している海面水温で割ることで、海洋貯熱量と海氷最大面積の線形性を緩和する意味がある。

df1234_div=df1234.copy()
#'ht'を海洋貯熱量を海面水温で割ったもの、'st'を海氷最大面積を海面水温で割ったものとする
df1234_div['ht']=df1234_div['heat_volume']/df1234_div['sea_temperature']
df1234_div['st']=df1234_div['sea_ice_area']/df1234_div['sea_temperature']
df1234_div=df1234_div.replace([-np.inf],np.nan)
df1234_div=df1234_div.dropna()
df1234_div=df1234_div.reset_index() #補正した変数を説明変数とする 
x2_div = df1234_div[['ht','st','sea_temperature']]
y2_div= df1234_div[['sea_level']]
x1_2_div = df1234_div[['heat_volume']]
x2_2_div = df1234_div[['sea_ice_area']]
x3_2_div=df1234_div[['sea_temperature']]

3-5. 交絡変数を含めた重回帰分析

以下のコードで重回帰分析を行う。

train_X_2_div, test_X_2_div, train_y_2_div, test_y_2_div = train_test_split(x2_div, y2_div, test_size=0.3, random_state=42)
model_lr_conf_div = LinearRegression()
model_lr_conf_div.fit(train_X_2_div, train_y_2_div)
 #予測値 
train_y_pred_conf_div=model_lr_conf_div.predict(train_X_2_div)
test_y_pred_conf_div=model_lr_conf_div.predict(test_X_2_div) #偏回帰係数 
df_coef_conf_div = pd.DataFrame(model_lr_conf_div.coef_.reshape(1,3),index=['偏回帰係数'],columns=[['ht', 'st','sea_temperature']])
display(df_coef_conf_div) #定数項 
print(model_lr_conf_div.intercept_)
print('')
print('決定係数')
print('訓練データ',model_lr_conf_div.score(train_X_2_div,train_y_2_div))
print('テストデータ',model_lr_conf_div.score(test_X_2_div, test_y_2_div))
print('自由度調整済み決定係数') #自由度調整済み決定係数 
def adjusted_r2_score_conf(y_actual_conf_div, y_pred_conf_div, number_dimensions_conf_div):
    # 決定係数
    coefficient_of_determination_conf_div = r2_score(y_actual_conf_div, y_pred_conf_div)
    # サンプルサイズ
    sample_size_conf_div = len(y_actual_conf_div)

    return 1 - (1 - coefficient_of_determination_conf_div) * (sample_size_conf_div - 1) / (sample_size_conf_div - number_dimensions_conf_div - 1)

# 訓練データ
print('訓練データ',adjusted_r2_score_conf(train_y_2_div, train_y_pred_conf_div, train_X_2_div.shape[1]))
# テストデータ
print('テストデータ:',adjusted_r2_score_conf(test_y_2_div, test_y_pred_conf_div, test_X_2_div.shape[1]))

Table8から、Table2と比べると自由度調整済み決定係数は下がるが、海氷面積を交絡変数で割った変数は負の値を得ることができた。次にVIF値を確認してみる。

def create_vif_df(c):
    c=add_constant(c)
    df_vif=pd.DataFrame()
    df_vif['features']=c.columns
    df_vif['VIF Factor']=[variance_inflation_factor(c.values, i) for i in range(c.shape[1])]
    return df_vif
vif_bef=create_vif_df(train_X_2_div)
vif_bef

Table9から、VIF値が7.32と7.05でかなり高いことがわかる。よって、海洋貯熱量と海氷最大面積の説明変数間で相関が生まれている裏付けになったが、良いモデルとは言えないと考える。

3-6. 主成分分析

2-2の訓練データとテストデータを用いて主成分分析を行う。

from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
model_lr_pca=LinearRegression() #標準化を行う 
sc=StandardScaler()
train_X_std = sc.fit_transform(train_X)
test_X_std = sc.transform(test_X) #主成分分析のインスタンスを生成 
pca = PCA(n_components=2)
train_X_pca = pca.fit_transform(train_X_std)
test_X_pca = pca.transform(test_X_std)
model_lr_pca.fit(train_X_pca,train_y)
 #予測値 
train_y_pred_pca=model_lr_pca.predict(train_X_pca)
test_y_pred_pca=model_lr_pca.predict(test_X_pca) #偏回帰係数 
df_coef_pca = pd.DataFrame(model_lr_pca.coef_.reshape(1,2),index=['偏回帰係数'],columns=[['heat_volume', 'sea_ice_area']])
display(df_coef_pca) #定数項 
print(model_lr_pca.intercept_)
print('')
print('決定係数')
print('訓練データ:',model_lr_pca.score(train_X_pca,train_y))
print('テストデータ:',model_lr_pca.score(test_X_pca, test_y))
print('自由度調整済み決定係数') #自由度調整済み決定係数 
def adjusted_r2_score_pca(y_actual_pca, y_pred_pca, number_dimensions_pca):
    # 決定係数
    coefficient_of_determination_pca = r2_score(y_actual_pca, y_pred_pca)
    # サンプルサイズ
    sample_size_pca = len(y_actual_pca)

    return 1 - (1 - coefficient_of_determination_pca) * (sample_size_pca - 1) / (sample_size_pca - number_dimensions_pca - 1)

# 訓練データ
print('訓練データ:',adjusted_r2_score_pca(train_y, train_y_pred_pca, train_X_pca.shape[1]))
# テストデータ
print('テストデータ:',adjusted_r2_score_pca(test_y, test_y_pred_pca, test_X_pca.shape[1]))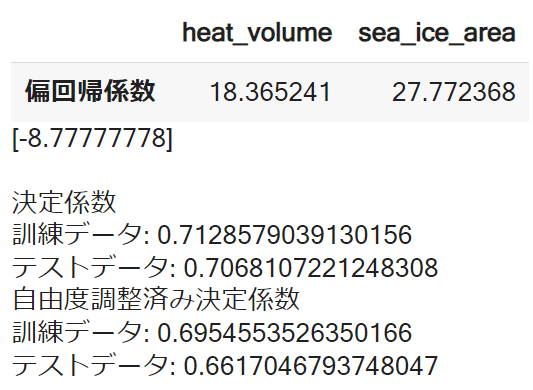

Table10の結果は主成分分析により、新しく作成した軸の元で得られた回帰係数であるため(今回は2軸に分けた)、2軸それぞれの式を算出する。軸をそれぞれ、pc0、pc1と定義する。主成分分析の軸の引き方は以下の2ステップである。
①まず、一番分散の大きい方向に軸を引いていく。
②２本目以降は残った次元の中で次に分散が大きい方向に軸を引く。
イメージとしては、以下の図の通り。赤線がpc0、黄線がpc1。

以下では、それぞれの軸に対する回帰式を算出した。

df_pca=pd.DataFrame(pca.components_,index=[f'pc{i}' for i in range(len(pca.components_[0]))],columns=['heat_volume','sea_ice_area'])
df_pca

次に元の回帰式に変換する。主成分分析によって新しくできた式をz=ax+byとする。そして、pc0の式をx=mx+ny、pc1の式をy=px+qyとする。よって、元の変数の回帰式に戻すと、z=a(mx+ny)+b(px+qy)=(am+bp)x+(an+bq)yとなる。a,bはTable10の値であり、m,n,p,qはTable11の値である。また、xは海洋貯熱量、yは海氷最大面積である。まず、am+bpを求める。

((model_lr_pca.coef_[0][0]*df_pca.iloc[0,0])+(model_lr_pca.coef_[0][1]*df_pca.iloc[1,0]))

結果は32.6242159313631

次にan+bqを求める。

((model_lr_pca.coef_[0][0]*df_pca.iloc[0,1])+(model_lr_pca.coef_[0][1]*df_pca.iloc[1,1]))

結果は6.651843366613377

以上の結果から、元の回帰式に変換すると、z=32.6x+6.65yとなる。海氷最大面積の係数が6.65で正の値となっている。期待していた負の値にはならなかった。

4. 結果

2-2では基本的な重回帰分析を実施した。得られた結果は、海洋貯熱量に関して、回帰係数は正になり一般的な理論と一致した。しかし、負になるはずの海氷最大面積の係数が正になってしまった。一方で、各説明変数と海面水位の単回帰分析をそれぞれ行うと、一般的な理論と一致し、海氷最大面積は負になった。よって、多重共線性の可能性を考え、3-5と3-6で解決策を施した。3-5では、回帰係数は理論と一致したが、多重共線性の問題が解決されなかった。3-6では主成分分析により、多重共線性は解決されたと考えるが、回帰係数は負にならないという結果になった。この一連の結果から考察をする。　

5. 考察

　上記の結果から、重回帰分析の視点から考えると海洋貯熱量と海氷最大面積が目的変数である海面水位に対して説明力を持つことを証明するのは難しいと考える。
　まず、多重共線性を解決するために仮定した交絡変数を用いた方法について議論する。交絡変数が分かっているケースは稀であり、今回もあくまで仮定であるため、良い方法ではないと考えることが出来る。次に主成分分析を用いて、多重共線性を解決する方法である。期待していた結果にはならなかったものの、軸を分けることで説明変数間を独立で捉えることができるという点で有効だと考えることができる。
　まとめると、重回帰分析で捉えるのではなく、それぞれを単回帰分析で見ることが最も有効であると考える。また、海面上昇の問題は地球温暖化による気温や水温の上昇が大きく関連していると考えると、温度で回帰分析をすることが有効なのではないかと考えることもできる。

6. 結論

目的変数である海面水位に対して、
①氷河/氷床に貯蔵されていた氷の融解
②水温が高くなることによる海水体積の膨張
以上の2点が説明能力を持つのかを検証するという成果物の目的に関しては、重回帰分析では上手くいかないという結論になった。

7. 反省

カウンセラーの方に教えていただいた、主成分分析を用いた後で回帰分析をすることで多重共線性を排除するやり方は新しい発見だったので勉強になった。また、重回帰分析の視点で一般的に言われている理論を確かめることは難しいということも学ぶことができた。