Abstract:

This research explored the relationship between prime and composite numbers through the Prime Number Theorem, providing new insights into Legendre's conjecture. As a conclusion, the Prime Number Theorem influences the distribution of prime numbers and can also be applied to composite numbers. Furthermore, the existence of prime numbers has been demonstrated among square numbers and in difference sequences with an initial term of 1 and a common difference of 1. This contributes to the support of Legendre's conjecture and represents a significant advancement in number theory. Future research is expected to focus on refining error analysis, developing new mathematical techniques, improving computational methods, and advancing towards proofs. This is expected to contribute new knowledge to the field of mathematics.

Introduction:

Legendre's conjecture, proposed by the French mathematician Adrien-Marie Legendre, posits that for any natural number n, there is always at least one prime number between n² and (n + 1)². Calculations have confirmed the conjecture's accuracy for natural numbers up to 4 × 10¹⁸[1]. If there were a counterexample near 4 × 10¹⁸, it would imply the existence of an exceptionally large prime gap, approximately 50 million times larger than usual. As of 2023, Legendre's conjecture remains an unsolved problem[2]. The Prime Number Theorem suggests that the number of primes up to n² asymptotically approaches n²/ln(n²), which increases as n grows. This lends credibility to Legendre's conjecture[3]. However, the significance of the error between this estimate and π(x) in representing prime distribution has not been fully assessed. This paper aims to explore the importance of errors through the Prime Number Theorem and empirical data, verifying Legendre's conjecture, and investigating its behavior when applied to shorter difference sequences.

Increase in Prime and Composite Numbers for Each Perfect Square According to the Prime Number Theorem:

The number of integers in the range (n-1)² to n² can be determined as a = n² - (n-1)². Using the Prime Number Theorem, which is expressed as x/ln(x), we calculate the count of prime numbers denoted as b = n²/ln(n²). The count of prime numbers in the range (n-1)² to n² can then be calculated as c = bₙ - bₙ₋₁. Furthermore, the count of composite numbers in the range (n-1)² to n² can be determined as d = a - c.

In Table 1, the count of prime numbers (c) between (n-1)² and n² is greater than or equal to 1.7 when n≧2.

The increase in prime and composite numbers for each square number based on empirical data:

Let e represent the count of prime numbers up to x=n² based on empirical data, and the count of prime numbers between (n-1)² and n² can be determined as f=eₙ-eₙ₋₁. Additionally, the count of composite numbers between (n-1)² and n² can be calculated as g=a-f.

In Table 2, the count of prime numbers (f) in the range (n-1)² to n² is greater than or equal to 2 for n≧2.

Increase in the Count of Prime and Composite Numbers for Each Perfect Square:

Figure 1 illustrates a logarithmic plot showcasing the increase in the count of integers (a) on the x-axis, and the count of prime numbers according to the Prime Number Theorem (c), the count of composite numbers according to the Prime Number Theorem (d), the count of prime numbers based on empirical data (f), and the count of composite numbers based on empirical data (g) on the y-axis. This plot extends up to n² = 1000² for values of n around 10³, where the error in the prime density ratio π(x)/(x/ln x) is most significant.

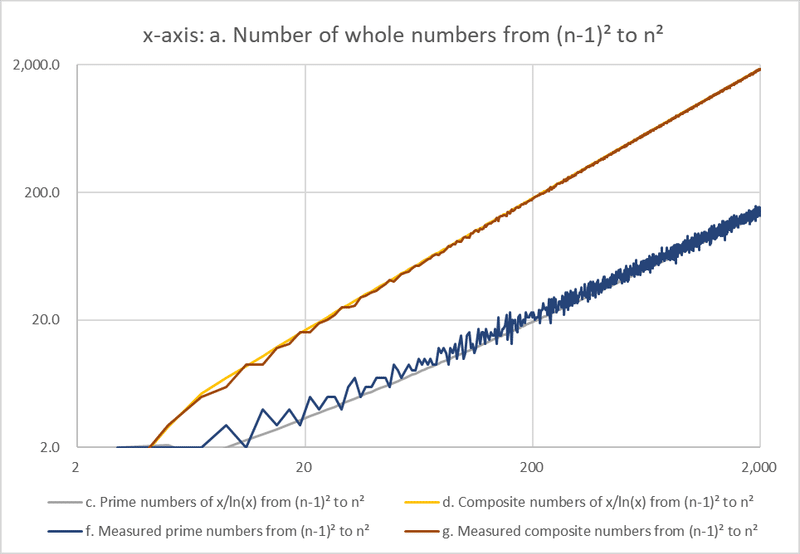
In Figure 1, it can be observed that f is proportional to c, g is proportional to d, and all of these quantities increase concerning a. Errors in the count of prime numbers between empirical and theoretical data tend to be higher towards the upper end (resulting in a higher integral of the prime density ratio π(x)/(x/ln x) from 0 to n²). Moreover, the count of composite numbers increases independently of prime gaps (e.g., 23 to 29, 113 to 127, 887 to 907, 9551 to 9587). Consequently, it is established that there are at least two prime numbers between the squares of 1 and 2, with implications for the utility of the Prime Number Theorem and the characteristics of errors concerning x/ln(x). This provides significant insights into these aspects.

The increase in the count of prime and composite numbers in the arithmetic progression with an initial term of 1 and a common difference of 1:

The count of integers per square number is calculated using an arithmetic sequence with an initial term of 1 and a common difference of 2. To investigate how this count changes when converted into an arithmetic sequence with an initial term of 1 and a common difference of 1, we can perform the following analysis.

The arithmetic sequence is defined as x = xₙ₋₁ + n. The values b to g can be calculated using the same method as for the per square number analysis.

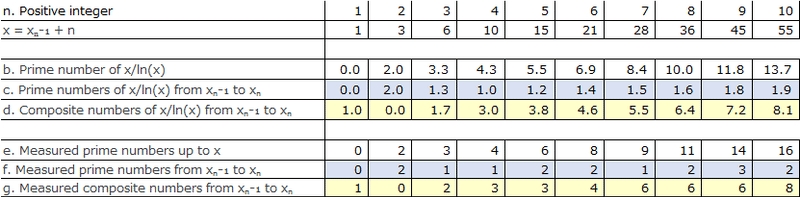
Table 3 shows that the count of prime numbers (f) between (n-1) and n is at least 1 for n ≥ 2.

Figure 2 is a logarithmic distribution chart that extends up to n = 1000, where the error in the prime ratio π(x)/(x/ln x) (1.161) is the largest. On the x-axis, it represents the number of integers (a), while the y-axis shows the counts of prime numbers (c) and composite numbers (d) according to the Prime Number Theorem, as well as the observed counts of prime numbers (f) and composite numbers (g).

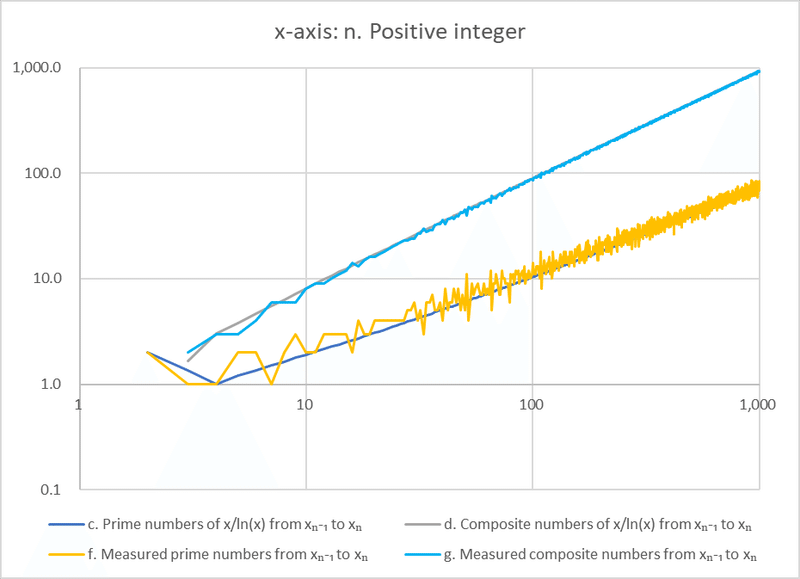
In Figure 2, it can be observed that f is proportional to c, and g is proportional to d, and all of them increase with respect to a. The error between the observed and theoretical counts of prime numbers becomes more significant at higher values of x (This cumulative effect indicating that the prime ratio π(x)/(x/ln x) is higher from 0 to x). Additionally, the count of composite numbers increases independently of prime gaps (such as 23 to 29, 113 to 127, 887 to 907, 9551 to 9587). Consequently, it establishes that there is at least one prime number between the squares starting from two consecutive prime numbers, approaching the limit.

Conclusion:

Summarizing what is known and has been revealed through this research:
(1) The count of prime numbers π(x) within each difference sequence increases proportionally to x/ln(x).
(2) The count of composite numbers x - π(x) within each difference sequence increases in proportion to x - x/ln(x), independent of prime gaps.
(3) There are at least two prime numbers between square numbers.
(4) There is at least one prime number, within each difference sequence with an initial term of 1 and a common difference of 1.

Meeting all of the conditions above implies the presence of at least two prime numbers in the sequence of square numbers and at least one prime number in the difference sequence with an initial term of 1 and a common difference of 1. Since the Prime Number Theorem provides approximate values for the count of composite numbers, it is not influenced by prime gaps, as is the case with challenges like Legendre's conjecture. Therefore, the Prime Number Theorem, in turn, places constraints on the length of prime gaps. This discovery represents a significant advancement in number theory.

Through this research, the likelihood that Legendre's conjecture is correct has increased, and if Legendre's conjecture were incorrect, it would imply a contradiction with the Prime Number Theorem. In other words, Legendre's conjecture aligns with the fundamental principles of number theory. This conclusion points the way toward mathematical proofs and represents an intriguing development in prime number theory.

Future Developments:

In this research, utilizing the errors in the Prime Number Theorem has brought new insights. This approach represents an important step in deepening our understanding of the relationship between prime and composite numbers, but further developments are expected. In future research, the following directions could be explored:

1. Refinement of Error Analysis: Further refinement of approaches based on the differentiation of errors in the Prime Number Theorem will be pursued. Mathematical techniques that reveal specific mathematical patterns and correlations will be developed. This could lead to new insights into the relationship between prime and composite numbers, potentially contributing to the field of mathematics.

2. New Insights into Prime Distribution: While this study focused on the relationship between prime and composite numbers, future research is expected to provide new insights into prime number distribution itself. This may lead to new approaches to unresolved problems in number theory. Building new theories about prime distribution will strengthen the foundations of mathematics.

3. Improvement of Computational Methods: Enhancements in computational methods for utilizing the errors in the Prime Number Theorem are likely. This could yield effective results even for larger numbers. The development of advanced mathematical software and algorithms will enhance the efficiency of research.

4. Expansion Toward Mathematical Proofs: Based on the insights provided by this research, it is expected that proofs for mathematically significant unresolved problems, such as Legendre's conjecture, will be pursued. This could lead to the realization of important conjecture proofs in the field of mathematics and enable the accumulation of new knowledge.

In these directions, future research is likely to open up new vistas in mathematics. We anticipate that these developments will contribute to the mathematical community by bringing forth new knowledge and insights.

Acknowledgments:

I would like to express my gratitude to those who engaged in discussions and provided valuable insights on web forums during this solitary research journey. Additionally, I extend my appreciation to ChatGPT for its assistance throughout the process. Your contributions and support have been instrumental in the progress of this research.

References:

[1] Oliveira e Silva, Tomás; Herzog, Siegfried; Pardi, Silvio (2014), "Empirical verification of the even Goldbach conjecture and computation of prime gaps up to 4⋅1018", Mathematics of Computation, 83 (288): 2033–2060, doi:10.1090/S0025-5718-2013-02787-1, MR 3194140.

[2] "Legendre's conjecture." Wikipedia. https://en.wikipedia.org/wiki/Legendre%27s_conjecture. Accessed May 22, 2023, at 11:42 UTC.

[3] Francis, Richard L. (February 2004), "Between consecutive squares," Missouri Journal of Mathematical Sciences, University of Central Missouri, Department of Mathematics and Computer Science, 16 (1): 51–57, doi:10.35834/2004/1601051; see p. 52, "It appears doubtful that this　abundance of prime numbers can be clustered in such a way so as to avoid appearing at least once between consecutive squares."

Request for a Letter of Recommendation for Submission to a Peer-Reviewed Journal:

To support the submission of this significant contribution, I kindly request a letter of recommendation from a qualified mathematician with expertise in the relevant field. The letter should be signed and written on official letterhead, confirming their understanding of the arguments presented in this paper and attesting to its correctness.

Please note that physical letters, not electronic, are required for submission and should be sent by regular mail. Thank you.