以下で、4n+1、4n+3の任意の奇数が1回ずつ並べることができるボトムアップ法の定式化によるコラッツ予想の証明をした。

世代リンクが保証された最大奇数は、何処までコラッツテーブルをジェネレートすればよいかは、連続する111₍₂₎の何処まで連鎖するかということだけなんです。
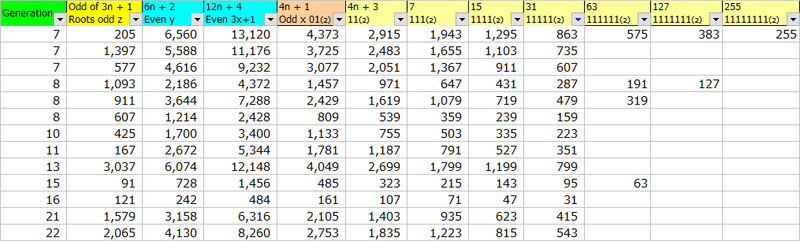
これは最大値を対数的上げて行けば、連続する1の数も増えていくので、発生できる世代が増えるのですべての任意の数が有限内で1に戻ることが言えるだけですね。下の表に上では、奇数を33まで生成して、3１＝11111₍₂₎は世代から漏れ、27は世代に入ってきませんが、奇数を3333まで生成すると、511₍₂₎＝111111111₍₂₎未満の世代に入るので、27も入ります。

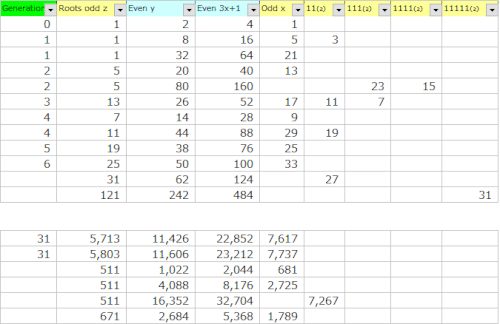
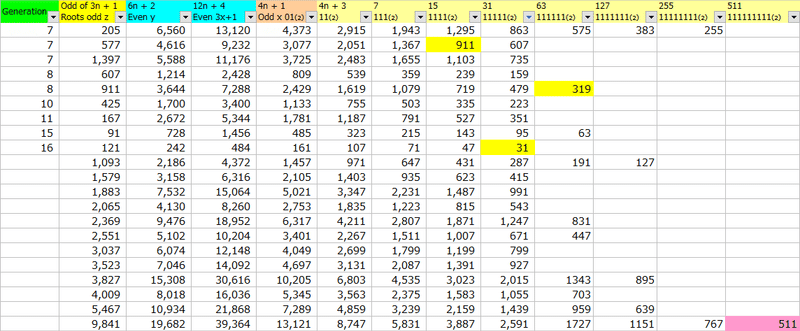
これは最大値というより、初期奇数27＜31というメルセンヌ数を通りますが、911も通りますので、511のメルセンヌ数まで、コラッツテーブルを作らないと、911の行が生成されないのです。
つまり２の５乗までの全奇数を通すには９乗まで、９乗まで全奇数を通すには２の13乗までのメルセンス数まで、２の４乗倍のメルセンス数までジェネレートする必要があります。

これをメルセンス数の桁と、世代リンクが保証された最大奇数と、世代数の関係は、

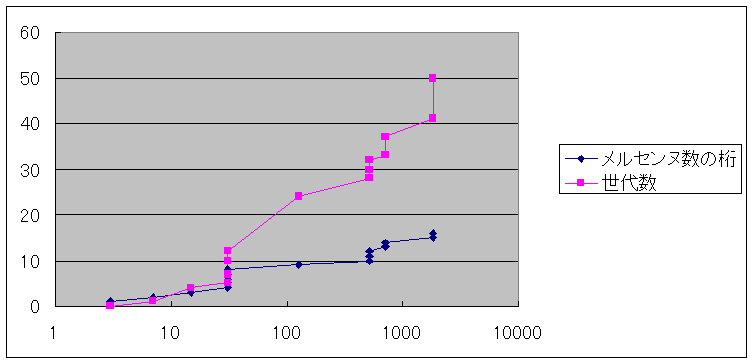
要は、任意の数に対して、その2進数の桁数の、２の４乗倍のメルセンス数までジェネレートすれば、ボトムアップ方式でコラッツテーブルができると言うことです。

全奇数をテーブルの一つの位置にマップできると言うことは、すべての山（RootsOddの谷から3x+1の偶数を頂として右側のOddを谷）をつくれるということだから、コラッツは、任意の奇数の桁数＋3ビットのメルセンス数以下をジェネレートすれば、任意の数に対する山はリンクしてくるので、メルセンス数の桁の最大数をそれに設定すれば、ボトムアップできるので、任意の数は無限ではないんです。

だから27は二進数では5桁＋3ビット＝8ビットのメルセンス数＝255の3ｘ＋1の偶数の最大値は、13120までジェネレートすれば、31までの数値は全部繋がります。
もっといえば、最終桁が0011(2)になるルートに入るように、ルートを準備＝任意の桁のメルセンス数をピークに準備すれば、1に入る全ルートが揃います。

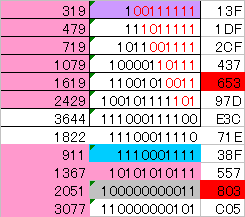
だから任意の数の桁数の1に到達する、もしくは1からボトムアップするために全ルートを用意できる有限なメルセンス数がある＝最大数があるということです。

もっといえば、自然数の並びの奇数は4n+1の4n+3と交互に出てきますが、コラッツ数列では、あるメルセンス数をピークとして、4n+1群と4n+3群の子供たちが形成されることが重要です。