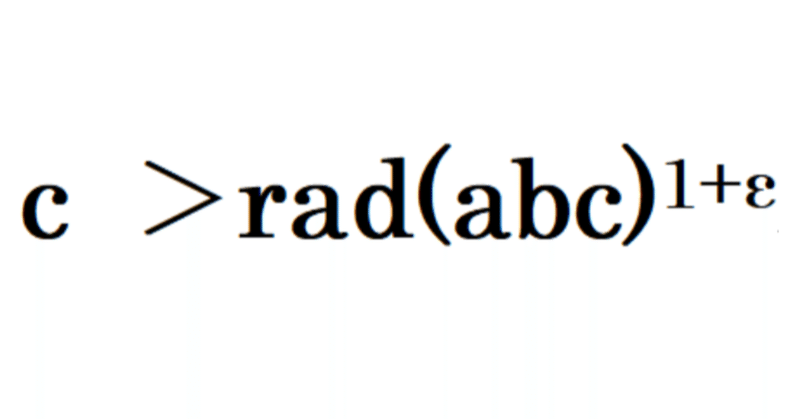
Breaking the weak ABC conjecture?
Introduction
The weak ABC Conjecture is a mathematical problem that predicts that if A+B=C and the triples (A,B,C) are positive integers that are coprime to each other, then there are only finitely many triples (A,B,C) that are not positive real number i>0 and C<rad(ABC)¹⁺ⁱ. This memo attempts to prove that there are an infinite number of triples (A, B, C) where A is 1 and C is the squared of the Mersenne number (2ⁿ-1).
Example of the triple (A,B,C) that is C/rad(C)>rad(AB)
A + B = C with A = 1.
C = B + 1. (1)
Since B and C in (Equation 1) are coprime to each other, the triples (A, B, C) are coprime to each other. Let C in (Equation 1) be the square root of the Mersenne number (2ⁿ-1)[3], then the relation with B is
(2ⁿ - 1)² = 2ⁿ⁺¹(2ⁿ⁻¹ - 1)² + 1. (2)
C / rad(C) > rad(AB) is obtained by removing A = 1 from (Equation 2),
C / rad(C) ≥ (2ⁿ - 1) > 2(2ⁿ⁻¹ - 1) ≥ rad(B). (3)
There are innumerable triples (A, B, C) that are coprime to each other with C / rad(C) > rad(AB).
Example of the triples (A, B, C) that is C>rad(ABC)¹⁺ⁱ
Let us look at the ratio of C:rad(ABC)¹⁺ⁱ in (Equation 2) with exponentiation 1+i>1 in the following pattern.
(2²⁽³ˆⁿ⁾ - 1)² = 2²⁽³ˆⁿ⁾⁺¹(2²⁽³ˆⁿ⁾⁻¹ - 1)² + 1. (4)
For example, an ABC triple with n = 0 and n = 4.
n=0:1 + 2³ = (3)²
:
n=4:
1
+
2¹⁶³x47x127x1289x178481x3188767x45076044553x14808607715315782481
=
(3⁵x7x19x73x163x2593x71119x87211x135433x262657x97685839x272010961)²
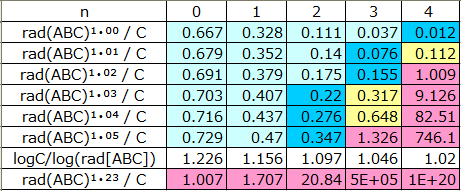
Varying the exponentiation (1+i) from 1.00 to 1.05 and 1.23, it obtain,
Conclusion
As n increases, the quality (logC/log[rad(ABC)]) is reduced, and when the positive real number i increases, rad (ABC) ¹⁺ⁱ / C exceeds 1, and the number of disjoint triples (A, B, C) becomes finite. However, it is possible to make the positive real number (i) infinitely close to zero.
This makes it impossible to determine the boundary between the finite and the infinite.
Therefore, without computational limits, the weak ABC conjecture can be violated by the myriad of disjoint triples (A, B, C) that satisfy the condition C> rad (ABC) ¹⁺ⁱ.
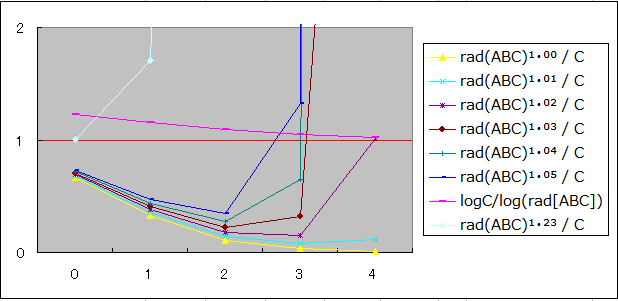
and The ratio of rad (ABC) ¹⁺ⁱ / C on the vertical axis
この記事が気に入ったらサポートをしてみませんか?
