なぜAIを考える時にベクトルを「矢印」と捉えるべきではないのか。
実際には矢印として考えたほうがいい例外もあります。

たとえば、特徴空間の任意の２点の引き算や足し算をするとき。
矢印のメタファーが使えます。

あるベクトルAから別のベクトルBを引いたベクトルCは、BからAへ伸びる矢印としてイメージするのは大丈夫です。

この性質を利用して、プロンプト芸が成り立つケースもあります。
たとえば画像生成系AIで使われるネガティブプロンプトはそういう性質を使っています。

しかし、根本的に、我々が普段イメージする二次元の矢印で示されるベクトルと、十次元以上の高次空間のベクトルは、全く異なる性質をもっていると考えるべきです。低次のベクトルと、高次のベクトルでは、共通する要素はあるけれども、それはごく一部に過ぎないということです。

例を挙げましょう。

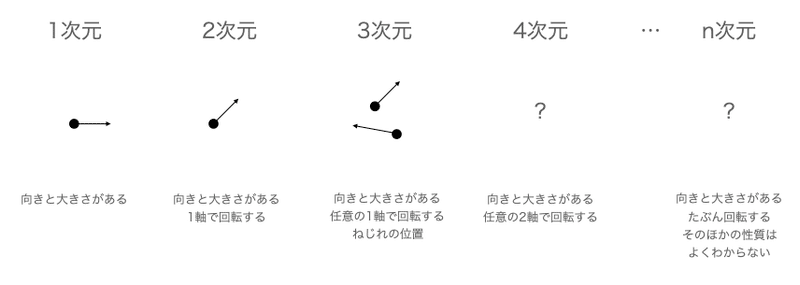
1次元のベクトルは、正負の向きと大きさを持ちます。
数直線上に引かれた矢印のイメージです。

2次元のベクトルは、上下左右に広がる平面上に向きと大きさを持ったベクトルで、1次元ベクトルにはなかった性質である「回転」というものが生まれます。また、1次元ベクトルにはなかった「垂直」という考え方が生まれます。

3次元のベクトルは、2次元のベクトルの性質に加えて、空間方向に回転します。ちなみに2次元の時の「回転」は、常に平面に対して垂直な軸での回転しかありませんでした。また、2次元のベクトルは平行でないものは常に延長すると交差していましたが、3次元のベクトルは「ねじれの位置」というものが存在し、平行でもなく交差もしていないベクトルが生まれます。

ところが3次元の回転は、任意の1軸に対して回転します。この時点で回転の性質が2次元のものとは根本的に異なります。

この3次元空間における「回転」の解決はものすごく難しい問題の一つです。任意軸周りの回転を矛盾なくスムーズに表現するためには、四元数という相異なる三つの虚数単位から成る複素数が必要になります。

4次元のベクトルは、任意の2軸に対して回転します。イメージできますか?これは相当難しい話になってしまいます。回転軸ベクトルも四次元で、その二つを固定しないと回転が表現できないという話になります。

おそらく5次元のベクトルは任意の3軸に対して回転すると考えられます。

しかし、ここまでくると、そもそも「回転とは何で、何のためにするのか」という意味がよくわからなくなってきます。これを求める学問も世の中にはありますが、AIではほとんど使いません。

このように、次元が一つ上がるごとに新しい性質が一つ以上うまれます。
我々は四次元以上の空間を直感的に体験することはできません。

そこで、「写像」という道具を使います。
二次元でいう正方形が、三次元である立方体で、四次元では超立方体と呼ばれるものになります。

ここに示したのは、四次元超立方体の三次元断面の二次元射影です。
本当に超立方体がどんな形か知りたければ、四次元的な回転を加えてさまざまな角度にアニメーションするしかありません。それでも不思議な形に変化するだけで、実際にどんなものかイメージすることは不可能になります。

四次元超立方体は、たとえば「表」とか「裏」とかいう概念も三次元とは違います。四次元球(超球)はもっと複雑です。

五次元以上にも同様のものが存在すると思われます。
人工知能が扱う次元数は、少なくて10次元、多くて5万次元です。

次元が一つあがるだけでも全く未知の性質が次々と発見されるのに、5万次元を把握するのに、矢印のイメージがほとんど役に立たないことをおわかりいただけたでしょうか。

もちろん、高次元空間は、角度を固定すれば、より下位の次元を再現することができます。たとえば、平面に直線を引けば一次元が再現でき、三次元空間に平面を置けば二次元が再現できます。