水力発電の発電機として用いている誘導モーターはベクトル制御により安定的に回生運転しています。このベクトル制御系の演算には平方根演算が頻出します。

ほとんどの小規模なマイコンではハードウェア的に平方根演算ができません。ハードウェアの制約を意識する事なくC標準ライブラリのsqrt()関数を用いて平方根を求めることはできますが、ソフトウェアで平方根を演算するのでランタイムの実装によっては重くなってしまいます。

そこで、計算法を工夫してそこそこ高速に平方根を求めるアルゴリズムを考えます。

よく知られた方法としてニュートン法による漸化式を用いる方法があります。

まず、√aのニュートン法による漸化式は以下のように与えられます。この式は2次収束します。

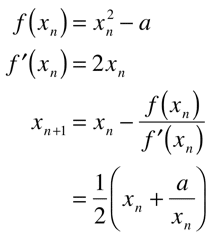
ここで、演算の都合上、単に√aの漸化式を用いるよりも、1/√aの漸化式を用いた方が式中に除算が無いため、まず1/√aを求めた後にaを乗算して√aを得ます。

また、アルゴリズム実装の都合上、共通項をh_nとして式を変形し、ついでに3次収束も求めておきます。

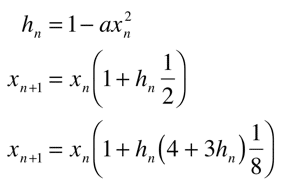
ニュートン法の漸化式はあらかじめ初期値を求めておく必要があります。そこで、浮動小数点数の符号化法に着目し、指数部と仮数部を分解して計算することで1/√aの折れ線近似を得ます。これを初期値として与える事で、少ないステップ数で十分な精度の平方根演算ができます。(B:指数部の値, H:仮数部の値, 赤:1/√a, 青:近似値)

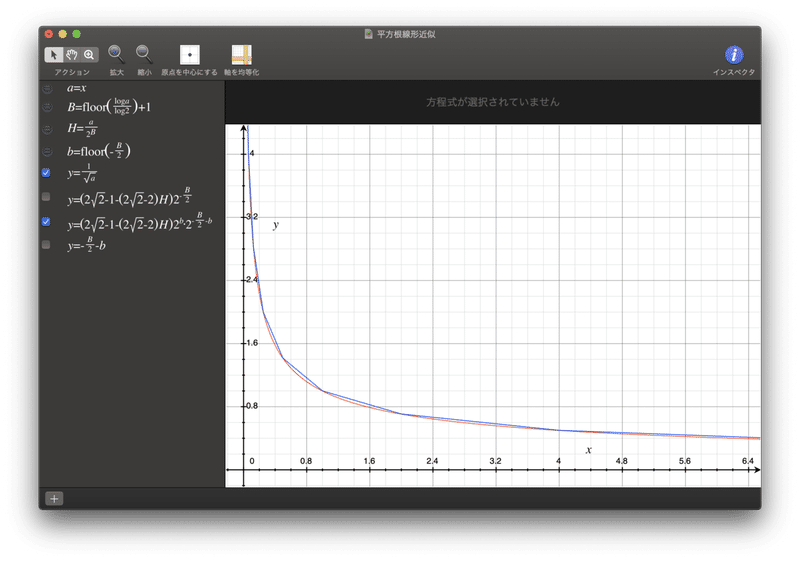
実際にこの方法で1/√aを求めるC言語による実装例を以下に示します。ニュートン法の漸化式は、最初のステップで演算コストに対して収束が早い3次収束の式を用いて計算します。その後精度を優先して2次収束の式で計算して仕上げます。

static inline float a_rsqrtf(float a, const float _exc) {
    if (a > 0.0f) {
        const float t_2r2rt[] = {1.00000000000000000E+00f, 1.41421356237309505E+00f};
        long e;
        float h, r = 1.82842712474619010E+00f - 8.28427124746190100E-01f * frexpf(a, &e);
        
        r  = ldexpf(r * t_2r2rt[e & 0x00000001], -e >> 1);
        h  = a * r * r;
        r *= 1.875f - h * (1.25f - h * 0.375f);
        a *= 0.5f;
        r *= 1.5f - a * r * r;
        r *= 1.5f - a * r * r;
        
        return r;
    }
    
    return _exc;
}

また、この水力発電の発電機として使用している誘導モーターの数理モデルは鉄損成分も含んでいます。鉄損抵抗は周波数の約0.6乗に比例して変化します。この0.6乗も同様の方法で効率的に計算します。

0.6乗を得るために、5乗根の逆数のニュートン法による漸化式を求めます。

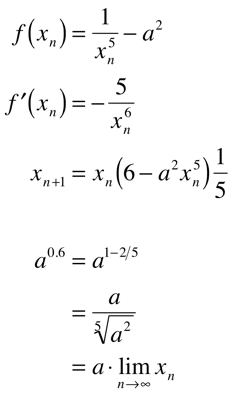
同様に、5乗根の逆数の折れ線近似を初期値とします。

5乗根の逆数を求める実装例は以下のようになります。

static inline float a_r5rtf(float a, const float _exc) {
    if (a > 0.0f) {
        const float t_2r5rt[] = {1.00000000000000000E+00f, 1.14869835499703501E+00f, 1.31950791077289426E+00f, 1.51571656651039808E+00f, 1.74110112659224828E+00f};
        long e, f;
        float h, r = 1.29739670999407001E+00f - 2.97396709994070014E-01f * frexpf(a, &e);
        
        f  = (long)ceilf((float)e * 0.2f);
        r  = ldexpf(r * t_2r5rt[5 * f - e], -f);
        a *= 0.2f;
        h  = r * r;
        r *= 1.2f - a * r * h * h;
        h  = r * r;
        r *= 1.2f - a * r * h * h;
        h  = r * r;
        r *= 1.2f - a * r * h * h;
        h  = r * r;
        r *= 1.2f - a * r * h * h;
        
        return r;
    }
    
    return _exc;
}

これにより、ベクトル制御系の演算で頻出する平方根や鉄損抵抗の0.6乗を効率的に計算できます。

#アルゴリズム #ニュートン法 #平方根