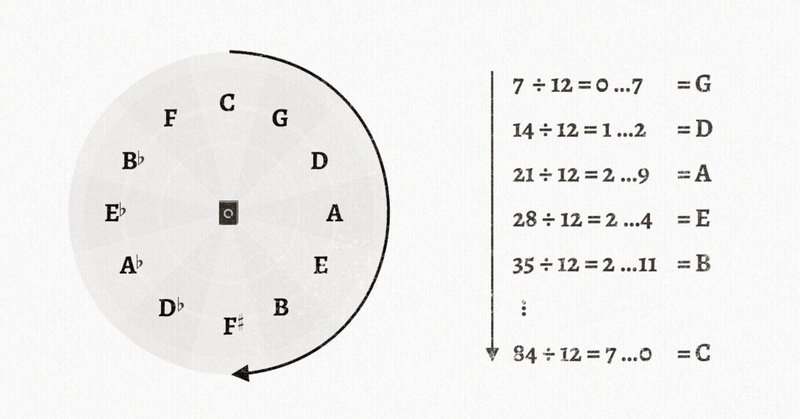
五度圏が12音を網羅する数学的証明
音楽理論にておなじみの「五度圏」は、便利アイテムです。時計のように、Cから完全5度ずつ進んでいくと、12回で一周して元に戻ってくる。
しかし、なぜ完全5度(=7半音)刻みで回ると綺麗に各音を1回ずつ拾って一周できるのでしょうか?
感覚的には納得しているけど、きちんと証明できますかと言われると、すぐにつらつらとは説明できない。その証明方法を、Twitterを通じて色んな人に教えて頂いたので、備忘録としてここに記しておきます。
五度圏がやっていること
まず五度圏が計算としてやっている内容を確認すると、それは次のようなものです。
・半音を1とすると、数を7ずつ足して新しい音を得る。
・数が12(=オクターブ)を超えた場合はそれを抜いて余りをとる。
・余りが0になったら、それは一周を終えたということである。
だから計算としては、「7の段を12で割ってその余りをとる」という作業をひたすら繰り返している。
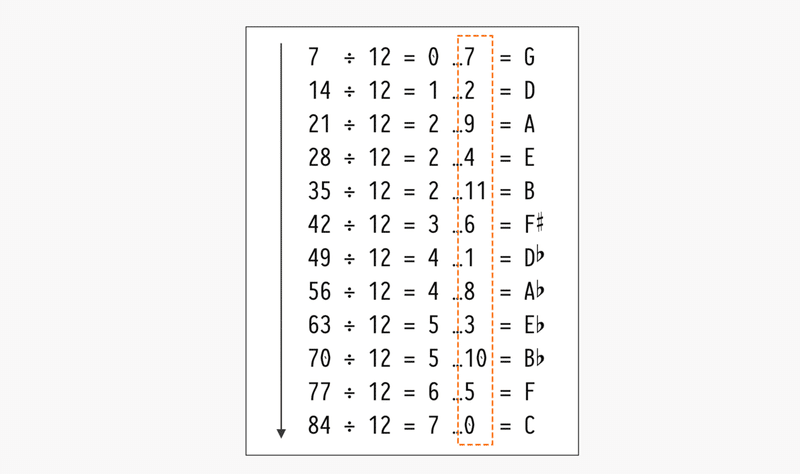
見てのとおり、余りが綺麗にばらけていて、数字がカブることは一度もない。「五度圏が12音を綺麗に網羅していく」という現象は、数の世界に置き換えると「7の倍数を12で割っていっても、全然余りがカブらない」ということなのだ。
これは「7」と「12」という数字が「絶妙に相性の悪い数字」だからこうもすれ違っていくのだなというのは、まず直感的に分かります。「相性の悪い数字」というのは具体的には、公約数が1しか存在しないこと、すなわち互いに素であることを指します。
「互いに素」がキーワード
これは逆を考えると分かりやすく、もし6半音ずつ進む「増4度圏」を作ろうとすると、「6」と「12」の相性が良すぎて、あっという間に一周してしまいます。
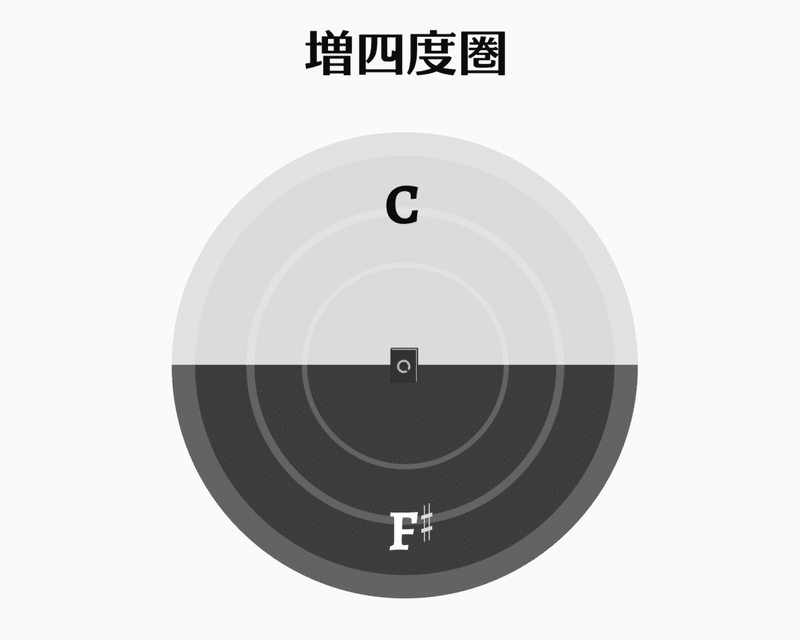
ご覧のとおり、CとF♯(G♭)以外の音が全く得られない。これは同様にして12の約数関係にある2・3・4でも同じことが言えます。
・2ずつ = Cホールトーンスケールのメンバー6人しか集まらない
・3ずつ = Cdim7のメンバー4人しか集まらない
・4ずつ = Caugのメンバー3人しか集まらない
したがって、ちゃんと12人のメンバーを集める可能性が残されているのは、12と互いに素である「1」か「11」、もしくは「7」か「5」ということになります。
1と11については、単に半音ずつずれて進んでいくだけなので、これが12音を順に拾っていくことには何の疑問もありません。しかし7(=完全5度)と5(=完全4度)に関しては飛び飛びで音を拾っていく形になるので、直感的に真だとは言い切れないものがあるわけです。ここのところを、ちゃんと証明したい!
「背理法」による証明プロセス
そんなわけで、証明したいのは7と12のように「互いに素なふたつの正の整数」があったときに、片っぽの倍数をもう片っぽの数字で割っていったとき、「一周して余りが0になるまでのあいだ、余りが全て異なる」ということです。
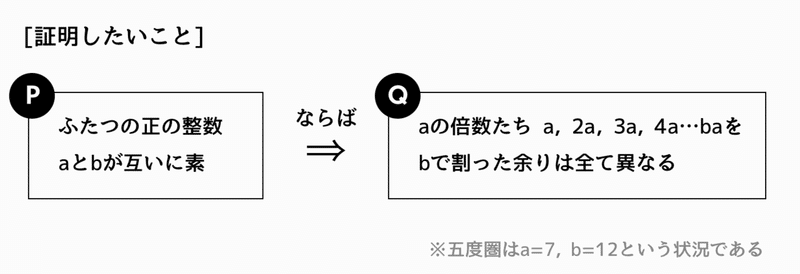
論理問題らしく、「PならばQ」の形で記述してみました。
この手の証明で活躍するのが「背理法」である。あえて証明したいことと逆の状況を想定して矛盾を導くという、名探偵みたいなやり口の証明法です。一応「背理法」の詳細なプロセスを先に確認しておきます。
まず結論部分(Q)をあえて反対にして、「もし余りにカブりが生じていたら」というシチュエーションを仮定する。そして「その状況でaとbが互いに素でしたというパターンはあり得るのだろうか?」を考える。
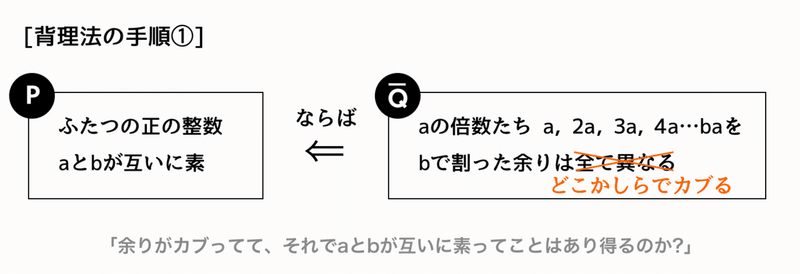
で、頑張るんだけどもどうしても矛盾が生じてしまって、その結果として「じゃあ余りがカブってるなら、aとbは絶対に互いに素ではないんだな…」という結論が得られる。
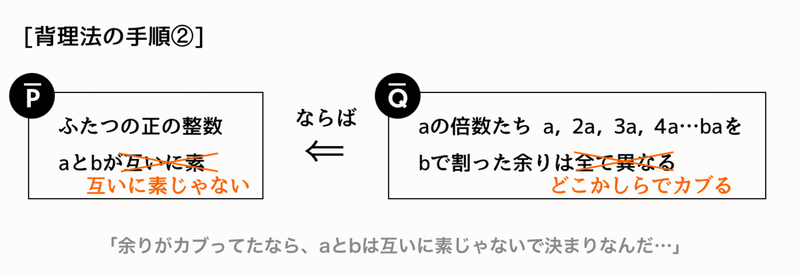
ここで論理思考の出番。「QでないならPでない」が証明されたのだから、自動的に対偶である「PならばQ」、すなわち元々言いたかった命題が証明されるという寸法である。
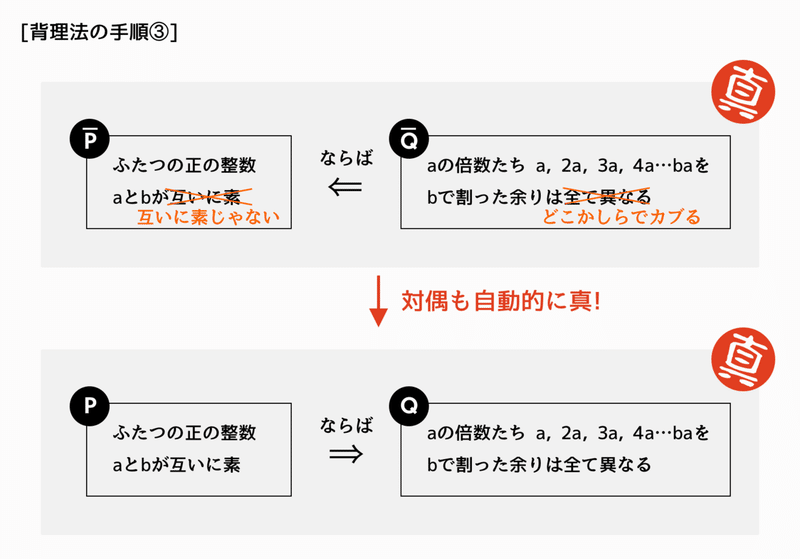
それでは実際に、証明をしていきます…
「背理法」で証明する
倍々していく数をa、割る数をbとする。a,bはともに自然数で、互いに素である。そして異なる2つの自然数をm,n(1≦m<n<b)、余りがカブったという状況を仮定し、そのカブった余りをrとする。
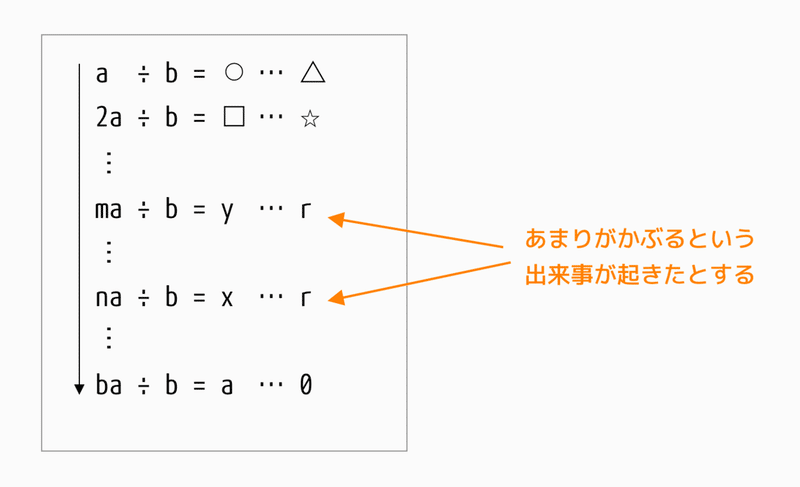
余りがカブった二箇所を数式で表すと以下のとおり。
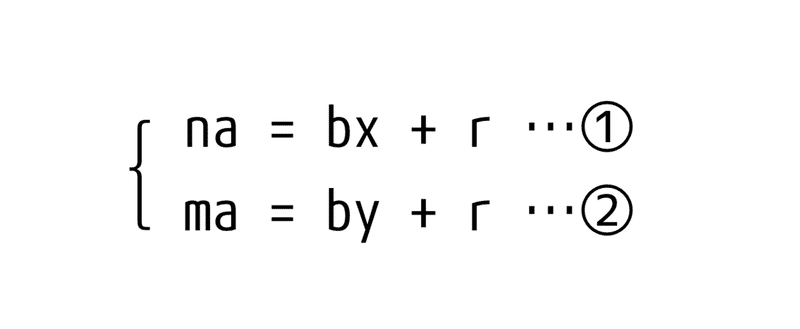
①-②で新しい式を作る。
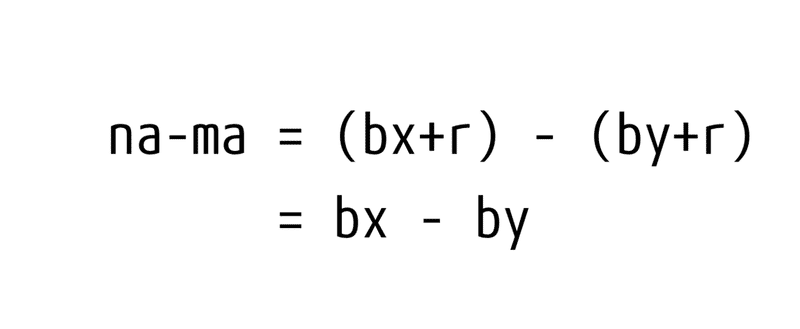
左辺、右辺それぞれを共通因数でくくると
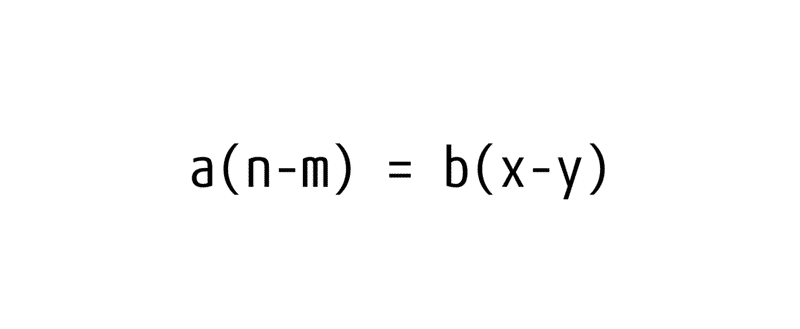
a,bが互いに素であるので、イコールが成り立つためには(n-m)がbの倍数でなければならない。しかし最初に「1≦m<n<b」という条件から始まっているので、n-m<bであるから「n-mがbの倍数」というのはありえない。ここに矛盾が生じる。
したがって、「余りがカブったのなら、aとbは互いに素ではない」と結論づけられる。よって対偶から、aとbが互いに素ならば、aの倍数たちa, 2a, 3a, 4a…baをbで割った余りは全て異なる。 (証明おわり)
12種類の異なる余りが生成されるのだから、五度圏が12音をきっちり網羅するということが分かりました。
─────────✂︎──────────
合同算術を使う
別の方法として、「合同算術」の分野を活用する方法もあります。合同算術というのは、簡単にいうと「剰余に特化した計算を考える数学の分野」で、高校数学Aの範囲に「合同式」というのがあったはずです(今はどうだかわからない)。
合同算術は、剰余に関する法則や定理をいっぱい発明していて、例えば「2の30乗を3で割った余りを求めよ」みたいな無理難題に対し、いちいち2の30乗を計算しなくても法則を駆使して余りだけなら簡単に弾き出せる。そういうことを研究する分野です。
12音の音階にまつわる問題は、上で見てきたように12で割った「余り」部分を論じるわけなので、合同算術との相性がピッタリなのです!٩( 'ω' )و
▼合同式
今回の五度圏の話でも既に明らかなとおり、「余り」というのは割る数以上になることはなく、延々とリセットされてサイクルします。
「7半音上も、19半音上も、12音ループの世界では同じことだ」というのを、合同算術では次のように言い表します。

12でループする世界線なので、12が「法」と呼ばれます(かっこいい)。この「法」のもとでは、7も19も平等なのだ。これを「合同」と表現する。
ちなみにこれはマイナスの数も同様で、「7半音上(=P5↑)も5半音下(=P4↓)も結局同じこと」というのを合同式で表すと…

こうなります。こんなふうに「剰余ワールド」を式で表現していくことで、合同算術は様々な法則を見つけ出してきたのです。
「中国の剰余定理」で証明する
改めて、今回証明したい内容はこちら。

今回の証明法によくマッチするように、周期の始まりを「7(=五度圏を1歩進んでGに着いたところ)」ではなく「0(=てっぺんのC)」からに設定しました。
さてこれを証明するのにピッタリな定理があって、それが「中国の剰余定理」です。

表現が難しいので、合同算術の書法を崩して平素な言い方に直すと次のような感じになります。

まだ文字が5種類もあってややこしいですが、「○○余るという条件に当てはまるxは1つしかない」的なことを言っていて、今回の「余りカブリ」に関係のある定理だということは見えたかと思います。
▼定理を改造する
さて、証明をするために必要なプロセスはたったひとつ、mに0を代入することです。そうすると「aで割るとm余り」という部分が「aで割ると0余り」となり、「aの倍数である」と同じ意味になります。

もうこれで、証明完了です。「余りがnになるxは、1サイクルの中では1つしかない」ということですから、これはまさに「余りがカブらない」ということを文字を使って表現しているに他なりません。
一応「7」と「12」を代入して、今回の五度圏話に当てはまるようにするとこうです。

合同算術の分野の人たちが「中国の剰余定理」という定理を作ってくれたおかげで、手間をかけずに証明ができました!
ちなみにこの定理も、元を辿れば背理法で証明される定理だそう。積み重ねの上に今があります。
─────────✂︎──────────
感覚的に分かることでも数学的に証明するとなると大変なものがありました。実践的な理論を構築するにあたって数学はさほど必要ではないですけども、こう理論の根底を支える存在として数学が役立っています。
今回、背理法を使った証明は @netai2yuto7さん、中国の剰余定理を使った証明は@music_shioさんから教えて頂きました。ありがとうございます( ˊ̱˂˃ˋ̱ )
この記事が気に入ったらサポートをしてみませんか?
