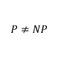こんにちは、これが294本目の記事となったすうじょうです。今日は、大学数学の解説記事です。今回の内容は、集合論より集合を解説します。本記事は一部高校数学と同じ内容を含みますが、大学数学の記事として書いています。(2022/03/14:内容を追加しました)

集合の重要性

高校数学の数学Ⅰで集合という概念が初めて登場する。大学数学においても重要な知識の一つで、記号論理や線形代数などとともに大学１年生のはじめに学ぶべき内容の一つである。例えば、数学において、関数を定義するとき、関数がどのような定義域なのかを説明するとき、集合が用いられる。

また、数学の抽象的な議論に慣れていくことができるように、記号論理による定義などを行う。よって、すでに解説している「記号論理」シリーズの内容を理解していることが望ましい。ただ、抽象的な定義だけでなく、理解の助けになるように直観的な説明も入れている。

このシリーズでは、集合どうしの演算を定義した後、「二項関係」、「半順序関係」、「同値関係」、「写像」、「集合の濃度」について解説する。公理的集合論は含まない。

集合とは

集合とは

集合とは、「もの」の集まりのことである。高校では、数の集合のみを取り扱っている場合が多いと思うが、集合としては以下のようなものも認められる。

日本人(日本国籍を持つ人)の氏名の集合
アルファベットの集合

ただし、何でも集合として認められるかというとそうではない。例えば、以下のようなものは認められない。

①身長が高い人の集合
②丸いものの集合

①では、身長が高いというのは具体的に何cm以上なのかというのが分からない。②では、丸いというのが漠然としている言葉で明確に定義されていない。このような理由から上の2つは集合として認められない。ただし、身長が高い人や丸いものというのをそれぞれ明確に定義した場合は集合として認められる。

つまり、集合としては、集合に含まれる「もの」と含まれない「もの」が明確に判断できるもののみが認められる。

記号の意味

集合に含まれる「もの」を要素または元という。
これについては、以下のように書くことができる。
$${a \in A}$$
この読み方については、「$${a}$$は集合$${A}$$の要素である」、「$${a}$$は$${A}$$に属する」などがある。
また、
$${a \notin A}$$
と書いたとき、$${a}$$は集合$${A}$$の要素ではないことを意味する。

また、集合の略記として、以下の記号が数学の教科書等で利用されることがあるので、ここで説明する。
$${\N}$$は自然数全体の集合を意味する。ただし、0を含める場合と含めない場合があるので注意する。
$${\Z}$$は整数全体の集合を意味する。
$${\Bbb{Q}}$$は有理数全体の集合を意味する。
$${\R}$$は実数全体の集合を意味する。
$${\Complex}$$は複素数全体の集合を意味する。
また、これらについては右肩に＋が付くと正の数、－が付くと負の数を表す。例えば、$${\R ^{+}}$$は正の実数を意味する。

集合の記法

集合を定義・表現する方法は2種類ある。
1つ目は、外延的記法で例えば以下のようにして書く。
$${A=\{1,2,3,4,5,6,7,8,9\}}$$
$${B=\{a,b,c,d,e,…\}}$$
空集合$${\empty}$$は、この記法では$${\{\}}$$と表せる。
2つ目は、内包的記法で一般形と条件による定義を用いて例えば以下のように書く。
$${\N=\{x | xは自然数\}}$$
$${C=\{2n | n \in \Z\}}$$
$${D=\{m | m \in \N, 1 \leq m \leq 4\}}$$
上の集合$${D}$$の例の{}の中の「,」はかつの意味で用いていることに注意する。

集合を外延的記法で表現するとき、同じ要素を複数回書いても、それは特に意味をなさない。また、書き並べる順番には特に意味はない。

集合の要素は集合でもよい

高校数学で扱ってきた集合は、集合を要素とするようなものはない。しかし、集合の要素は集合であってもよい。こうなると、{}が多くてややこしくなるので、集合の要素が何なのかを正しく知るためには{と}の対応関係によく注意しなければならない。また、集合を要素に含む集合の要素数を数える場合は、もっとも外側の{}に注目して数える必要があるので注意する。

$${E=\{1,\{2,3\},4\}}$$
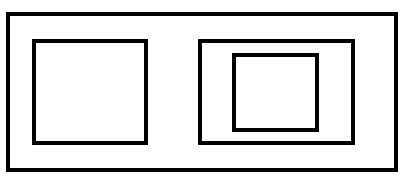
$${F=\{\empty,\{\empty\}\}}$$
$${G=\{1,\{1\},\{\{1\}\}\}}$$
上で述べたように$${\empty}$$は$${\{\}}$$と書いてもよい。

これらの例において、各集合の要素は次のようになる。
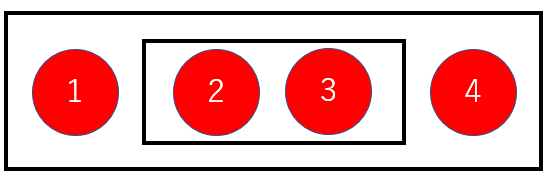
集合$${E}$$の要素は、$${1}$$と$${\{2,3\}}$$と$${4}$$の3つである。
集合$${F}$$の要素は、$${\empty}$$と$${\{\empty\}}$$の2つである。
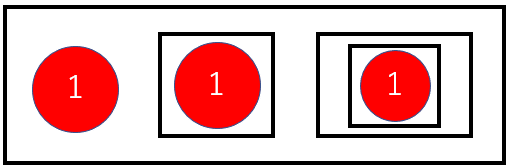
集合$${G}$$の要素は、$${1}$$と$${\{1\}}$$と$${\{\{1\}\}}$$の3つである。

以下にそれぞれの集合のイメージ図を書く。ただし、箱が集合で、箱の中に入っている数字の描かれた玉が$${1}$$などに対応しているものとする。

集合$${E=\{1,\{2,3\},4\}}$$

集合$${F=\{\empty,\{\empty\}\}}$$

集合$${G=\{1,\{1\},\{\{1\}\}\}}$$

演習問題1

問題1 次の(a)~(d)のうち、正しいものをすべて選べ。
(a)$${1 \in \{1,2,3\}}$$
(b)$${\{1\} \in \{1,2,3\}}$$
(c)$${\{1,2\} \in \{1,\{1,2\}\}}$$
(d)$${\empty \in \empty}$$

[方針]
$${a \in A}$$のとき、$${a}$$は集合$${A}$$の要素でなければならない
[解答]
(a),(c)
(b)は$${\{1\}}$$という要素が$${\{1,2,3\}}$$にないので、誤り
(d)は$${\{\} \in \{\}}$$とも書けるが、これは誤り

※(d)の補足として、$${\empty \in \{\empty\}}$$は正しい。

問題2 次の集合の要素数をそれぞれ求めよ。
(1)$${\{0,1,2,3,4\}}$$
(2)$${\{a,b\}}$$
(3)$${\empty}$$
(4)$${\{1,\{1.2\},\{3\}\}}$$
(5)$${\{\{1,2,3\}\}}$$

[解答]
(1) 5 (2) 2 (3) 0 (4) 3 (5) 1

最後に

今回は、大学数学の解説記事として、集合の基礎について解説しました。集合は、大学数学の基礎となる概念で、関数の理解などにも必要になります。この記事の続きとして、集合の関係・演算の解説記事を書く予定です。では。

この記事の続きは以下の記事です。