こんにちは、これが318本目の記事となったすうじょうです。今日は、大学数学の解説記事です。今回の内容は、大学数学の基礎となる記号論理より論理的同値や論理的帰結などを解説します。

この記事は、以下の記事の続きです。

命題論理

論理的同値とは

論理式$${P,Q}$$があり、それぞれを構成する命題変数の真理値すべての組み合わせについて、論理式$${P,Q}$$の真理値が一致するとき、論理式$${P,Q}$$は論理的に同値であるといい、$${P \equiv Q}$$と表す。

※これは「1 命題論理の基礎」で扱った同値$${↔}$$とは異なり、$${ \equiv}$$は論理記号ではなく、論理式の関係を表す記号として用いている。なお、論理的同値の記号として、$${\Leftrightarrow}$$が使われている場合もあるが、ここでは論理記号の同値と明確に区別するため$${\equiv}$$を用いる。

論理的同値であることを示す方法としては、真理値表を書き確かめる方法とすでに論理的同値だと分かっている変形を用いる方法がある。

また、$${P \equiv Q}$$であるための必要十分条件は、$${P \leftrightarrow Q}$$が恒真式であることである。

以下に、論理的同値な命題論理式を示す。

・ベキ等法則
$${P \land P \equiv P, P \lor P \equiv P}$$
・命題定数を含む論理式
$${P \land \textrm{T} \equiv P, P \lor \textrm{T} \equiv \textrm{T}, P \land \textrm{F} \equiv \textrm{F}, P \lor \textrm{F} \equiv P}$$
 ・交換法則(順序を交換できる)
$${P \land Q \equiv Q \land O, P \lor Q \equiv Q \lor P}$$
・結合法則(優先順位を変更しても結果は変わらない)
$${(P \land Q) \land R \equiv P \land (Q \land R),(P \lor Q) \lor R \equiv P \lor (Q \lor R)}$$
・分配法則(掛け算のように展開することができる)
$${P \land (Q \lor R) \equiv (P \land Q) \lor (P \land R),P \lor (Q \land R) \equiv (P \lor Q) \land (P \lor R)}$$
・二重否定
$${\lnot (\lnot P) \equiv P}$$
・排中法則
$${P \land \lnot P \equiv \textrm{F}, P \lor \lnot P \equiv \textrm{T}}$$
・ド・モルガンの法則
$${\lnot (P \land Q) \equiv \lnot P \lor \lnot Q, \lnot (P \lor Q) \equiv \lnot P \land \lnot Q}$$
・その他
$${P \rightarrow Q \equiv \lnot P \lor Q, P \leftrightarrow Q \equiv (P \rightarrow Q) \land (P \rightarrow Q), \\(P \land Q) \to R \equiv P \to (Q \to R)}$$

※含意式は、交換法則と結合法則が成り立たない。特に結合法則について、$${(P \to Q) \to R}$$と$${P \to (Q \to R)}$$は異なる論理式なので注意する。 

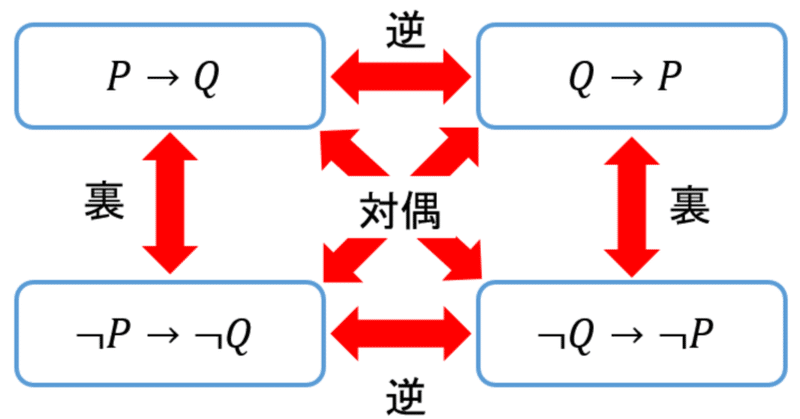
含意式の逆・裏・対偶

含意式$${P \to Q}$$があるとき、
前提と結論を入れ替えた論理式$${Q \to P}$$を逆、
前提と結論をともに否定した論理式$${\lnot P \to \lnot Q}$$を裏、
前提と結論をともに否定し入れ替えた論理式$${\lnot Q \to \lnot P}$$を対偶という。
これらの関係を図にしたものを図1に示す。

また、これらの真理値表を以下に示す。

表7:含意式とその逆・裏・対偶の真理値表

$$
\begin{array}{cccccccc}
P&Q&\lnot P&\lnot Q&P \to Q&Q \to P&\lnot P \to \lnot Q&\lnot Q \to \lnot P\\
\hline
\textrm{F}&\textrm{F}&\textrm{T}&\textrm{T}&\textrm{T}&\textrm{T}&\textrm{T}&\textrm{T}\\
\textrm{F}&\textrm{T}&\textrm{T}&\textrm{F}&\textrm{T}&\textrm{F}&\textrm{F}&\textrm{T}\\
\textrm{T}&\textrm{F}&\textrm{F}&\textrm{T}&\textrm{F}&\textrm{T}&\textrm{T}&\textrm{F}\\
\textrm{T}&\textrm{T}&\textrm{F}&\textrm{F}&\textrm{T}&\textrm{T}&\textrm{T}&\textrm{T}\\
\hline
\end{array}
$$

真理値表をみると、含意式$${P \to Q}$$とその対偶$${\lnot Q \to \lnot P}$$の真理値がすべての場合において一致していることがわかる。
ここから、$${P \to Q \equiv \lnot Q \to \lnot P}$$といえる。これは、対偶証明法が命題の証明技法として利用できる根拠となっている。

論理的帰結(妥当な推論とは)

この内容は記号論理の中でも論理学的な部分が多いので、飛ばしてもらっても構わない。

有限個の命題(前提)から1個の命題(結論)を導くことを推論という。数学における証明は推論の連なりと考えることができる。ここでは、証明・推論の妥当性について意味論的な立場(真偽によって妥当性を判断する立場)から述べる。

論理式$${F_1,F_2,…,F_n}$$と論理式$${G}$$について、$${F_1,F_2,…,F_n}$$がすべて真となるすべての場合について$${G}$$も真となるとき、$${G}$$を$${F_1,F_2,…,F_n}$$からの論理的帰結といい、$${F_1,F_2,…,F_n \vDash G}$$と表す。これは、論理式を用いると以下のようにいえる。

論理式$${(F_1 \land F_2 \land … \land F_n) \to G}$$が恒真式であるならば$${F_1,F_2,…,F_n \vDash G}$$である。

ここで、推論の中でも有名な三段論法(仮言三段論法)の妥当性について考える。三段論法とは、$${P \to Q}$$かつ$${Q \to R}$$ならば$${P \to R}$$であるというものである。

つまり、論理式$${((P \to Q) \land (Q \to R)) \to (P \to R)}$$が恒真式であるかどうか真理値表を書いて確かめればよい。

表8:三段論法の真理値表

$$
\begin{array}{ccccccc}
P&Q&R&P \to Q&Q \to R&P \to R&\footnotesize ((P \to Q) \land (Q \to R)) \to (P \to R)\\
\hline
\textrm{F}&\textrm{F}&\textrm{F}&\textrm{T}&\textrm{T}&\textrm{T}&\textrm{T}\\
\textrm{F}&\textrm{F}&\textrm{T}&\textrm{T}&\textrm{T}&\textrm{T}&\textrm{T}\\
\textrm{F}&\textrm{T}&\textrm{F}&\textrm{T}&\textrm{F}&\textrm{T}&\textrm{T}\\
\textrm{F}&\textrm{T}&\textrm{T}&\textrm{T}&\textrm{T}&\textrm{T}&\textrm{T}\\
\textrm{T}&\textrm{F}&\textrm{F}&\textrm{F}&\textrm{T}&\textrm{F}&\textrm{T}\\
\textrm{T}&\textrm{F}&\textrm{T}&\textrm{F}&\textrm{T}&\textrm{T}&\textrm{T}\\
\textrm{T}&\textrm{T}&\textrm{F}&\textrm{T}&\textrm{F}&\textrm{F}&\textrm{T}\\
\textrm{T}&\textrm{T}&\textrm{T}&\textrm{T}&\textrm{T}&\textrm{T}&\textrm{T}\\
\hline
\end{array}
$$

真理値表から$${((P \to Q) \land (Q \to R)) \to (P \to R)}$$は恒真式であることがわかった。よって、三段論法(仮言三段論法)は妥当な推論である。つまり、$${P \to Q, Q \to R \vDash P \to R}$$である。

演習問題2

問題3 ド・モルガンの法則$${\lnot (P \land Q) \equiv \lnot P \lor \lnot Q}$$が成り立つことを真理値表を用いて示せ。

[証明]

$$
\begin{array}{ccccccc}
P&Q&P \land Q&\lnot P&\lnot Q&\lnot (P \land Q)&\lnot P \lor \lnot Q\\
\hline
\textrm{F}&\textrm{F}&\textrm{F}&\textrm{T}&\textrm{T}&\textrm{T}&\textrm{T}\\
\textrm{F}&\textrm{T}&\textrm{F}&\textrm{T}&\textrm{F}&\textrm{T}&\textrm{T}\\
\textrm{T}&\textrm{F}&\textrm{F}&\textrm{F}&\textrm{T}&\textrm{T}&\textrm{T}\\
\textrm{T}&\textrm{T}&\textrm{T}&\textrm{F}&\textrm{F}&\textrm{F}&\textrm{F}\\
\hline
\end{array}
$$

真理値表より, $${\lnot (P \land Q) \equiv \lnot P \lor \lnot Q}$$である．$${\Box}$$

問題4 論理的同値関係$${P \to Q \equiv \lnot Q \to \lnot P}$$が成り立つことを同値変形によって示せ。

[証明]

$$
\begin{aligned}
P \to Q&\equiv \lnot P \lor Q\\
&\equiv \lnot P \lor \lnot \lnot Q\\
&\equiv \lnot (\lnot Q) \lor \lnot P\\
&\equiv \lnot Q \to \lnot P \qquad \qquad \Box\\
\end{aligned}
$$

問題5 肯定式$${P \to Q, P  \vDash Q}$$が妥当な推論であることを示せ。

[証明]
論理式$${((P \to Q) \land P) \to Q}$$が恒真式であることを示せばよい．

$$
\begin{array}{ccccc}
P&Q&P \to Q&(P \to Q) \land P&((P \to Q) \land P) \to Q\\
\hline
\textrm{F}&\textrm{F}&\textrm{T}&\textrm{F}&\textrm{T}\\
\textrm{F}&\textrm{T}&\textrm{T}&\textrm{F}&\textrm{T}\\
\textrm{T}&\textrm{F}&\textrm{F}&\textrm{F}&\textrm{T}\\
\textrm{T}&\textrm{T}&\textrm{T}&\textrm{T}&\textrm{T}\\
\hline
\end{array}
$$

真理値表より, $${((P \to Q) \land P) \to Q}$$は恒真式であり, $${P \to Q, P  \vDash Q}$$は妥当な推論である．$${\Box}$$

最後に

今回は、大学数学・記号論理の解説記事として、論理的同値や論理的帰結について解説しました。次回は、述語論理の解説記事となる予定です。では。

この記事の続きは以下の記事です。