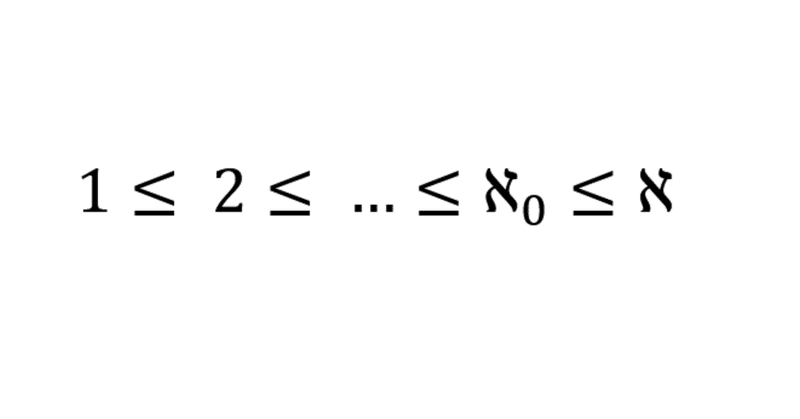
【集合】8 集合の濃度~可算無限と非可算無限~
こんにちは、これが339本目の記事となったすうじょうです。今日は、大学数学の解説記事です。今回の内容は、集合論より有限集合と無限集合を解説します。(指摘を受けて一部内容を訂正しました)
この記事は、以下の記事の続きです。
集合の濃度
集合の濃度(基数)
「集合の大きさ」を比較するとき、その判断基準としては、要素数が考えられる。これにより、要素が有限個の集合どうしなら比べることができる。しかし、要素数が有限でない集合、例えば$${\N}$$や$${\R}$$の場合、その「大きさ」を比較することはできない。なので、要素数が有限かそうでないかに関わらず、「集合の大きさ」を比較できるような概念を考える。
集合$${A}$$の大きさを表現する概念として、集合の濃度というものがあり、$${|A|}$$または$${\text{card}(A)}$$などと表す。濃度を用いて、数における等号や不等号のように「集合の大きさ」を比較する。
集合$${A}$$と$${B}$$において、
全単射$${f:A \to B}$$が存在するとき、$${A}$$と$${B}$$の濃度が等しく、$${|A|=|B|}$$と表す。
単射$${f:A \to B}$$が存在するとき、$${A}$$の濃度は$${B}$$の濃度以下であり、
$${|A| \leq |B|}$$と表す。
$${|A| \leq |B|}$$かつ$${|A|\neq|B|}$$であるとき、$${A}$$の濃度は$${B}$$の濃度より小さく、$${|A| < |B|}$$と表す。
濃度については、以下の性質が成り立つ。
反射律 $${|A|=|A|, |A| \leq |A|}$$
対称律 $${|A|=|B| \Rightarrow |B|=|A|}$$
推移律 $${|A|=|B| \land |B|=|C| \Rightarrow |A|=|C|, \\|A|\leq|B| \land |B|\leq|C| \Rightarrow |A|\leq|C|}$$
$${A \subseteq B}$$のとき、$${|A| \leq |B|}$$
具体的には以下のような基数を用いて集合の濃度を表現する。(詳しくは後で説明する)
集合$${A}$$の要素数が$${n}$$のとき、$${|A|=n}$$と表す。
自然数全体の集合$${\N}$$の濃度を、$${|\N|=\aleph_0}$$(アレフゼロ)と表す。
実数全体の集合$${\R}$$の濃度を、$${|\R|=\aleph}$$(アレフ)と表す。
※$${\aleph_0}$$を可算濃度、$${\aleph}$$を連続濃度という。
濃度の性質を用いると、例えば集合の包含関係$${\{1\} \subseteq \{1,2\} \subseteq … \subseteq \N \subseteq \R}$$より、以下の濃度の大小関係が導ける。
$${1 \leq 2 \leq … \leq \aleph_0 \leq \aleph}$$
有限集合と無限集合(可算無限と非可算無限)
集合$${A}$$と自然数の集合$${N=\{1,2,…,n\}}$$において、全単射$${f:N \to A}$$が存在するとき、集合$${A}$$を有限集合という。有限集合の基数は要素数と一致し、ある自然数$${n}$$を用いて$${|A|=n}$$と表す。ただし、$${A= \empty}$$のとき、$${|A|=0}$$とし、これも有限集合に含める。
有限集合ではない集合を無限集合という。
(無限)集合$${A}$$と自然数全体の集合$${\N}$$において、全単射$${f:\N \to A}$$が存在するとき、集合$${A}$$は可算無限集合であるという。可算無限集合の基数は、自然数全体の集合の濃度を表す基数$${\aleph_0}$$を用いて$${|A|=\aleph_0}$$と表す。直観的な意味としては、要素数は無限だが、ある規則で数え上げることができる集合。可算無限集合であることを示すには、集合のすべての要素と自然数を対応させるような規則を作る必要がある。
有限集合と可算無限集合を合わせて、数え上げることができる集合という意味で、可算集合という。
※可算集合について
可算無限という意味で、可算という言葉が用いられることもあるが、ここでは有限集合も含めている。
可算集合については、以下の性質が成り立つ。
有限個の可算集合の和集合は可算集合となる
可算集合の部分集合は可算集合となる
有限個の可算集合の直積集合は可算集合となる
可算集合の性質を用いると、例えば素数全体の集合が可算集合であることがわかる。
素数全体の集合を$${P}$$とすると、$${P \subseteq \N}$$である。
自然数全体の集合は可算集合より、素数全体の集合は可算集合である。
可算集合ではない無限集合を非可算無限集合という。直観的な意味としては、要素数が無限で、要素すべてを数え上げることができるような規則を作ることのできない集合。非可算無限集合であることを示すには、カントールの対角線論法で証明する。
非可算無限集合については、以下の性質が成り立つ。
集合$${A}$$の部分集合に非可算無限集合が存在するならば集合$${A}$$も非可算無限集合となる
非可算無限集合の具体例については、次回取り扱う。
有理数全体は可算無限集合である
ここからは、有理数全体$${\Bbb{Q}}$$が可算無限集合であることを示す全単射を考えていく。その試行錯誤を以下に書いてみる。
可算無限集合であることを証明するためには、有理数すべてと自然数を対応させるような規則を作る必要がある。
まず、考えやすいように、有理数全体ではなく、その部分集合である正の有理数全体の集合$${\Bbb{Q}^+}$$で考える。
愚直に0に最も近い有理数から順に大きくなっていくように自然数と対応させていくことを考えてみる。しかし、これは最初から詰まってしまう。そもそも有理数は無限に存在し、0に最も近い有理数は無限に考え続けられるからである。なので、何らかの工夫が必要となる。
そこで、有理数とはどういった数なのかその定義を確認する。有理数とは、分数の形で表せる数で、正の有理数を集合にすると$${\Bbb{Q}^+=\{\dfrac{p}{q} | p,q \in \N\}}$$となる。
ここで、1つ分母の値を決めたうえで、分子の数を1から数え上げて、すべて数えた後で、分母の値を変えていって対応させることを考える。しかし、自然数は無限にあるので1つ目の分母から2つ目の分母へ変えるタイミングがない。そこで、数え上げる方法を工夫してみる。そして、分母と分子の数の和$${p+q}$$が小さいものから順に正の有理数を数え上げると、うまく数え上げることができそうだとわかる。
しかし、ここで2つ問題が発生する。1つ目は、そもそも$${1/1,2/2,3/3}$$など等しい組み合わせが無数にあり、同じ数を重複して数えてしまっているというものだ。2つ目は、例えば、和が3の場合$${2/1,1/2}$$の2つがあり、その順番を考えなくてはならない。まず、最初の問題については、すべての正の有理数は1通りの既約分数で表すことができるという有理数の性質を思い出すと、解決できることが分かる。つまり、数える有理数を既約分数に限定すればよい。次に2つ目の問題について、和が等しい有理数については、例えば分母が小さい有理数から順に対応させると決めればよい。(分子が小さい有理数から順に対応させてもよい)
これで過不足なく一意に正の有理数を数え上げることができる。ここまでをまとめると、$${\Bbb{Q}^+=\{\dfrac{p}{q} | p,q \in \N,pとqは互いに素\}}$$を$${p+q}$$が小さいものから順に自然数と対応させる。ただし、$${p+q}$$が等しい分数については、分母$${q}$$が小さいものから順に対応させる。
具体的には、全単射写像$${f:\N \to \Bbb{Q}^+}$$は以下のようになる。
$${f(1)=\dfrac{1}{1},f(2)=\dfrac{2}{1},f(3)=\dfrac{1}{2},f(4)=\dfrac{1}{3},…}$$
これで、正の有理数全体$${\Bbb{Q}^+}$$は可算無限集合であるといえた。そして、有理数全体を考えると、$${\Bbb{Q}=\Bbb{Q}^+ \cup \Bbb{Q}^- \cup \{0\}}$$となる。ここで、$${\Bbb{Q}^-}$$は$${\Bbb{Q}^+}$$と同様に規則を考えると、可算無限集合であると分かる。よって、$${\Bbb{Q}}$$は可算集合の和集合なので、有理数全体の集合$${\Bbb{Q}}$$は可算無限集合である。つまり、$${|\N|=|\Bbb{Q}|=\aleph_0}$$である。
演習問題8
問題21 次の集合が可算無限集合であることを証明せよ。
(1) $${2\N=\{2,4,6,…\}}$$
(2) $${\Z=\{…,-2,-1,0,1,2,…\}}$$
[証明]
(1)
次のような写像$${f:\N \to 2\N}$$を考える
$${f:n \mapsto 2n \space (f(n)=2n)}$$
写像$${f}$$は全単射なので, $${2\N}$$は可算無限集合である$${\Box}$$
(2)
次のような写像$${g:\N \to \Z}$$を考える
$${g(n) = \begin{cases} \dfrac{n}{2} & nが偶数 \\ -\dfrac{n-1}{2} & nが奇数\end{cases}}$$
写像$${g}$$は全単射なので, $${\Z}$$は可算無限集合である$${\Box}$$
※(2)の写像については、具体的には$${g(1)=0,g(2)=1,g(3)=-1,g(4)=2,…}$$と対応していく。
問題22 次のことを証明せよ。
(1) $${A \subseteq B}$$のとき、$${|A| \leq |B|}$$となることを証明せよ。
(2) 可算無限集合$${A,B}$$の和集合$${C=A \cup B}$$は可算無限集合であることを証明せよ。
[証明]
(1)
$${A \subseteq B}$$より, 次のような写像$${\iota:A \to B}$$を考えることができる
$${\iota:x \mapsto x}$$
写像$${\iota}$$は単射なので, $${|A| \leq |B|}$$ $${\Box}$$
※写像$${\iota}$$のことを包含写像という。
(2)
$${A,B}$$は可算無限集合より, 以下のような写像$${f,g}$$が存在する
$${f:\N \to A, g:\N \to B}$$
ここで, 次のような写像$${h:\N \to C}$$を考える
$${h(n) = \begin{cases} f(\dfrac{n+1}{2}) & nが奇数 \\ g(\dfrac{n}{2}) & nが偶数\end{cases}}$$
写像$${h}$$は全単射なので, $${C=A \cup B}$$は可算無限集合である$${\Box}$$
※具体的には、$${h(1)=f(1),h(2)=g(1),h(3)=f(2),h(4)=g(2),…}$$と対応していく。
最後に
今回は、大学数学・集合論の解説記事として、集合の濃度について解説しました。次回は、今回の続きとして非可算無限集合の証明方法の解説記事です。では。
この記事の続きは以下の記事です。(この記事を投稿するタイミングで以前書いた記事を再編集しました)
この記事が気に入ったらサポートをしてみませんか?