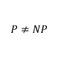
【集合】5 半順序関係と上界、最大元など
こんにちは、これが325本目の記事となったすうじょうです。今日は、大学数学の解説記事です。今回の内容は、1か月ぶりに集合論より半順序関係を解説します。今回は集合論のなかでも、主に情報系の数学(離散数学等)で取り扱われる内容です。
この記事は、以下の記事の続きです。
半順序関係
半順序関係の定義
集合$${A}$$上の二項関係$${R}$$が反射律、反対称律、推移律を満たすとき、$${R}$$を半順序関係あるいは単に半順序という。また、$${(A,R)}$$を半順序集合という。
一般に半順序関係の話をするとき、$${R}$$の代わりに順序を連想しやすい記号$${\leq}$$が使われることがあるが、この記事では大小関係の$${\leq}$$と区別するため、記号$${\sqsubseteq}$$を用いることとする。
ちなみに、この記事では掘り下げないが、集合$${A}$$上の二項関係$${R}$$が反射律、反対称律、推移律、完全律を満たすとき、$${R}$$を全順序関係あるいは単に全順序という。
半順序関係の例としては、子孫関係がある。ただし、自分自身は自分の子孫であるとする。その具体例を以下に示す。
$${A=}$${勇,和子,修,真由美, 恵, 翔太,大和,凛}上の二項関係$${R_D =}$$ {(勇,勇),(和子,和子),(修,修),(真由美,真由美),(恵,恵),(翔太,翔太),(大和,大和),(凛,凛),(大和,翔太),(大和,恵),(大和,修),(大和,真由美),(大和,勇),(大和,和子),(凛,翔太),(凛,恵),(凛,修),(凛,真由美),(凛,勇),(凛,和子),(恵,修),(恵,真由美),(恵,勇),(恵,和子),(修,勇),(修,和子)}とする。
$${(x,y)\in R_D}$$のとき、$${x}$$は$${y}$$の子孫($${y}$$は$${x}$$の祖先)という二項関係である。
この子孫関係は親子関係の反射推移閉包となっている。よって、子孫関係は$${R_D = }$${(大和,翔太),(大和,恵),(凛,翔太),(凛,恵),(恵,修),(恵,真由美),(修,勇),(修,和子)$${\}^*}$$と親子関係を用いて表現できる。
この二項関係$${R_D}$$は半順序関係の条件である反射律、反対称律、推移律をそれぞれ満たしている。
他の半順序関係の例としては、$${\N}$$上の二項関係$${\leq}$$がある。条件を満たしているかどうかは、「4 二項関係とその性質」で確認している。(さらに言えば、$${\N}$$上の二項関係$${\leq}$$は全順序関係である)
半順序集合の図示(ハッセ図)
半順序集合$${(A,\sqsubseteq)}$$を図示する方法の一つにハッセ図がある。ハッセ図は、半順序関係の推移的な関係を簡略的に表現した図である。ハッセ図では、半順序関係の反射的、推移的な要素を省略している。また、半順序関係$${\sqsubseteq}$$について、$${x \sqsubseteq y}$$のとき「$${y}$$は$${x}$$よりも大きい」と考え、「大きいもの」が図の上になるように配置することで順序を表現している。
$${(A,\sqsubseteq)}$$のハッセ図の書き方(直観的な説明)
以下、$${A}$$上の半順序関係$${\sqsubseteq}$$について、反射的、推移的な要素は除外して考える(一番近い関係のみを考える)
$${a \sqsubseteq b}$$のとき、$${b}$$の点を$${a}$$の点よりも上に配置する
$${c \sqsubseteq d}$$と$${e \sqsubseteq d}$$があるとき、$${c}$$の点と$${e}$$の点は同じ高さに配置する(このとき、$${c \sqsubseteq e}$$もあるときは$${c \sqsubseteq d}$$が$${\sqsubseteq}$$の推移的な要素となっていることを意味するのでその要素は除外する)
高さの差が一段の点どうしについて、$${a \sqsubseteq b}$$のとき$${a}$$の点と$${b}$$の点の間に線分を結ぶ
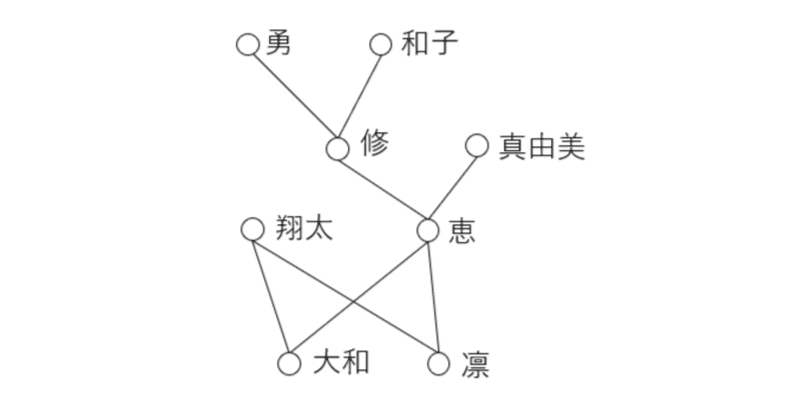
$${A=}$${勇,和子,修,真由美, 恵, 翔太,大和,凛}上の二項関係である子孫関係$${R_D}$$の場合、そのハッセ図は以下のようになる。
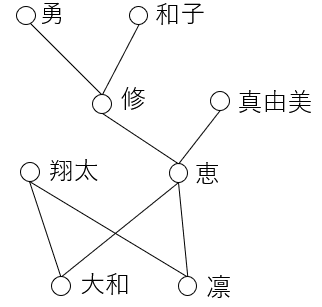
この例でいえば、線分があるのは直接の親子関係がある人どうしの間で、同じ高さにあるのは夫婦または兄弟姉妹となっている。また、線分をたどれば子孫関係にある人たちがわかる。(子孫関係のハッセ図は家系図となっている)
半順序集合で定義される概念
ここから半順序集合で定義される概念についてその定義を示していく。同じ概念が、微分積分学でも登場するが、それと同一のものである。
$${A}$$上の半順序関係$${\sqsubseteq}$$があるとき、$${A}$$の部分集合$${S}$$について以下のような概念を定義できる。
$${S}$$の上界$${\xLeftrightarrow{def} x \in A \space s.t. \space \forall y \in S, y \sqsubseteq x}$$
※上界をもつとき、$${S}$$は上に有界であるという。
$${S}$$の最大元$${\xLeftrightarrow{def} x \in S \space s.t. \space \forall y \in S, y \sqsubseteq x}$$
※$${S}$$の最大元は、$${\max S}$$ と表す。
$${S}$$の下界$${\xLeftrightarrow{def} x \in A \space s.t. \space \forall y \in S, x \sqsubseteq y}$$
※下界をもつとき、$${S}$$は下に有界であるという。
$${S}$$の最小元$${\xLeftrightarrow{def} x \in S \space s.t. \space \forall y \in S, x \sqsubseteq y}$$
※$${S}$$の最小元は、$${\min S}$$ と表す。
$${S}$$の上限(最小上界)$${\xLeftrightarrow{def} \min\{x|xはSの上界\}}$$
※$${S}$$の上限は、$${\sup S}$$または$${\textrm{lub} \space S}$$と表す。
$${S}$$の下限(最大下界)$${\xLeftrightarrow{def} \max\{x|xはSの下界\}}$$
※$${S}$$の下限は、$${\inf S}$$または$${\textrm{glb} \space S}$$と表す。
$${S}$$の極大元$${\xLeftrightarrow{def} x \in S \space s.t. \space \lnot \exists y \in S, x \sqsubset y}$$
ただし、$${x \sqsubset y \xLeftrightarrow{def} x \sqsubseteq y かつ x \neq y}$$とする。
$${S}$$の極小元$${\xLeftrightarrow{def} x \in S \space s.t. \space \lnot \exists y \in S, y \sqsubset x}$$
※集合によって、それぞれの概念にあてはまる要素が存在するかどうか異なる。
※それぞれの概念のハッセ図における考え方(直観的な説明)
$${A}$$の部分集合$${S}$$があるとき、
・$${S}$$の上界
$${A}$$の要素のうち、自身以外の$${S}$$の各要素から上へ線分をたどってつながっていて、$${S}$$のどの要素よりも上にあるもの($${S}$$の他すべての要素を上からおさえられる)
・$${S}$$の最大元
$${S}$$の上界のうち、$${S}$$の要素のもの
・$${S}$$の下界
$${A}$$の要素で、自身以外の$${S}$$の各要素から下へ線分をたどってつながっていて、$${S}$$のどの要素よりも下にあるもの($${S}$$の他すべての要素を下からおさえられる)
・$${S}$$の最小元
$${S}$$の下界のうち、$${S}$$の要素のもの
・$${S}$$の上限
上界の要素で、自身以外の$${S}$$の上界の各要素から下へ線分をたどってつながっていて、上界のどの要素よりも下にあるもの
・$${S}$$の下限
下界の要素で、自身以外の$${S}$$の下界の各要素から上へ線分をたどってつながっていて、下界のどの要素よりも上にあるもの
・$${S}$$の極大元
$${S}$$の要素で、その要素から上へ線分をたどってつながっている$${S}$$の要素がないもの
・$${S}$$の極小元
$${S}$$の要素で、その要素から下へ線分をたどってつながっている$${S}$$の要素がないもの
※$${S}$$の上界と下界について、それぞれ$${S}$$の要素も含まれることに注意する。
$${A=}$${勇,和子,修,真由美,恵,翔太,大和,凛}上の二項関係である子孫関係$${R_D}$$について、$${A}$$の部分集合$${S=}$${修,恵,翔太}として、上の概念それぞれを考える。
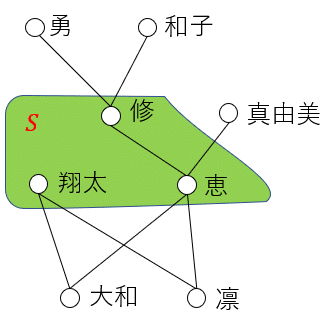
$${S}$$の上界 なし(翔太と修は子孫関係にない)
$${S}$$の最大元 なし
$${S}$$の下界 大和,凛
$${S}$$の最小元 なし
$${S}$$の上限 なし
$${S}$$の下限 なし
$${S}$$の極大元 修,翔太(翔太は祖先が$${S}$$の中にいない)
$${S}$$の極小元 翔太,恵
※例としては、少し難易度が高い気もしますが、各用語の定義か直観的な説明でしっかりと理解してほしいです。
ここで、上で定義した概念についての性質として以下が成り立つ。ただし、その証明は省略する。
$${S}$$の最大元、最小元、上限、下限はそれぞれ存在するならば唯一つしか存在しない
$${S}$$の最大元、最小元はそれぞれ$${S}$$の極大元、極小元となっている
$${S}$$の最大元、最小元は存在するならばそれぞれ$${S}$$の上限、下限と一致する
演習問題5
問題14 $${X}$$を要素数2以上の集合とするとき、次の各問に答えよ。
(1)$${2^X}$$上の二項関係$${\subseteq}$$(包含関係)が半順序関係であることを証明せよ。
(2)半順序集合$${(2^{\{a,b,c\}},\subseteq)}$$のハッセ図を書け。
(3)集合$${2^{\{a,b,c\}}}$$の部分集合$${S_1=\{\{a\},\{b\},\{c\},\{a,b\},\{a,c\}\}}$$があるとき、$${S_1}$$の上界、下界、最大元、最小元、上限、下限、極大元、極小元をそれぞれすべて求めよ。
(4)集合$${2^{\{a,b,c\}}}$$の部分集合$${S_2=\{\empty,\{a\},\{b\},\{a,b\}\}}$$があるとき、$${S_2}$$の上界、下界、最大元、最小元、上限、下限、極大元、極小元をそれぞれすべて求めよ。
[方針]
ハッセ図については、解答①と解答②のどちらの形でもよい
また、ハッセ図において同じ高さの要素については、並べる順番に特に決まりはない
(3)と(4)は、ハッセ図で考えても、半順序関係の要素と各用語の定義から考えてもよい。
[証明]
(1)
$${2^X}$$上の二項関係$${\subseteq}$$が反射律, 反対称律, 推移律を満たすことを示せばよい.
$${\forall A \in 2^X, A \subseteq A \space (\because 部分集合の定義)}$$
よって, 反射律を満たす.
$${\forall A, \forall B \in 2^X, A \subseteq B \land B \subseteq A \Rightarrow A=B \space (\because 集合の相等の定義)}$$
よって, 反対称律を満たす.
$${\forall A, \forall B, \forall C \in 2^X, A \subseteq B \land B \subseteq C \Rightarrow A \subseteq C \space (\because 部分集合の定義)}$$
よって, 推移律を満たす.$${\Box}$$
[解答①]
(2)
$${2^{\{a,b,c\}}=\{\empty,\{a\},\{b\},\{c\},\{a,b\},\{a,c\},\{b,c\},\{a,b,c\}\}}$$
$${\subseteq = \{(\empty,\{a\}),(\empty,\{b\}),(\empty,\{c\}),(\{a\},\{a,b\}),(\{a\},\{a,c\}),(\{b\},\{a,b\}),\\(\{b\},\{b,c\}),(\{c\},\{a,c\}),(\{c\},\{b,c\}),(\{a,b\},\{a,b,c\}),(\{a,c\},\{a,b,c\}),\\(\{b,c\},\{a,b,c\})\}^*}$$
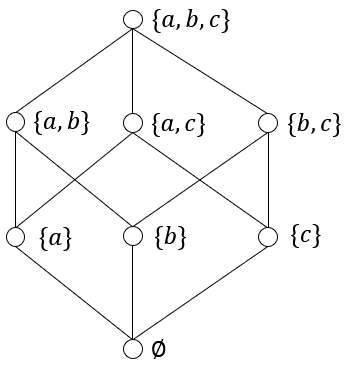
(3)
上界 $${\{a,b,c\}}$$
下界 $${\empty}$$
最大元 なし
最小元 なし
上限 $${\{a,b,c\}}$$
下限 $${\empty}$$
極大元 $${\{a,b\},\{a,c\}}$$
極小元 $${\{a\},\{b\},\{c\}}$$
(4)
上界 $${\{a,b\},\{a,b,c\}}$$
下界 $${\empty}$$
最大元 $${\{a,b\}}$$
最小元 $${\empty}$$
上限 $${\{a,b\}}$$
下限 $${\empty}$$
極大元 $${\{a,b\}}$$
極小元 $${\empty}$$
[解答②]
(2)
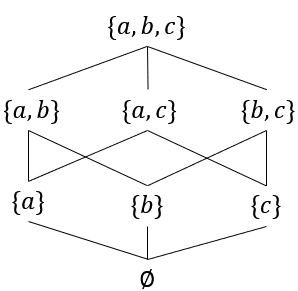
※(2)について、ハッセ図は半順序関係の要素を考えなくてもわかりやすい。
最後に
今回は、大学数学・集合論の解説記事として、半順序関係について解説しました。今回の内容は、前回の二項関係の内容を理解していることが前提です。次回は、同値関係と商集合の解説記事となる予定です。では。
この記事の続きは以下の記事です。
この記事が気に入ったらサポートをしてみませんか?