こんにちは、これが302本目の記事となったすうじょうです。今日は、大学数学の解説記事です。今回の内容は、集合論より集合どうしの関係を解説します。本記事はほとんどの内容が大学数学です。

この記事は、以下の記事の続きです。(2022/03/14に内容を追加しています)

部分集合

部分集合の基本

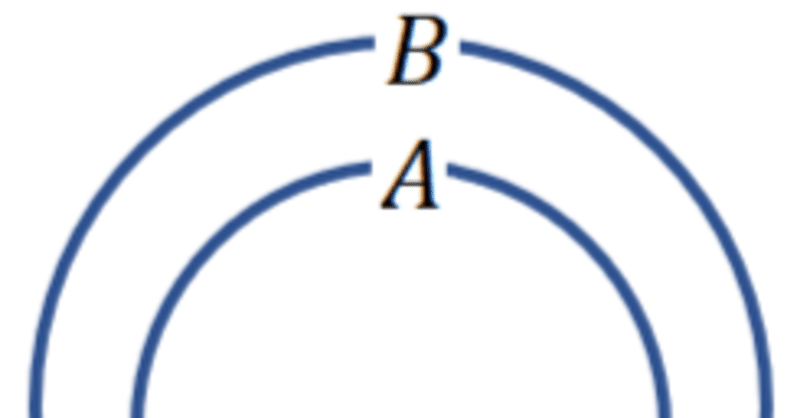
集合$${A}$$のすべての要素が集合$${B}$$の要素であるとき、集合$${A}$$は集合$${B}$$の部分集合であるといい、$${A \subseteq B}$$と表す。これをベン図で表すと図4のようになる。

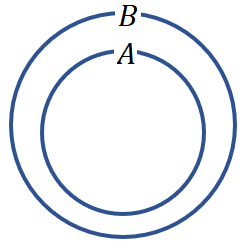
また、集合$${B}$$は集合$${A}$$の部分集合ではあるが、集合$${A}$$と一致しないとき、集合$${A}$$は集合$${B}$$の真部分集合であるといい、$${A \subsetneq B}$$と表す。

真部分集合は、集合どうしの関係を表すとき、2つが一致しないことを明示したいときに用いる。真部分集合の関係を満たす2つの集合について、$${A \subseteq B}$$などと表しても特に問題はない。

集合$${A}$$の部分集合の個数は、集合$${A}$$の要素数を$${|A|}$$とすると、$${2^{|A|}}$$となる。これは、集合$${A}$$の各要素について、部分集合に含める場合と含めない場合の2通りあり、これを$${A}$$の要素すべてで考えるためである。

※部分集合の記号について
ここでは、部分集合を$${A \subseteq B}$$、真部分集合を$${A \subsetneq B}$$と表しているが、教科書等によっては以下の表記もある。
部分集合$${A \subset B}$$と真部分集合$${A \subsetneq B}$$の組み合わせ
部分集合を表す他の記号:$${A \subseteqq B}$$
真部分集合を表す他の記号:$${A \subsetneqq B}$$

部分集合の厳密な定義

さきほどは、部分集合の定義を集合$${A}$$のすべての要素が集合$${B}$$の要素であるとしましたが、これは数学的に厳密な書き方ではありません。数学では、厳密な定義をするとき、よく論理記号を用います。ここでは、その記号を用いた部分集合の定義を紹介します。
※論理記号の解説記事は別に書いています。

$${A \subseteq B \xLeftrightarrow{def} \forall x(x \in A \to x \in B)}$$

※$${\xLeftrightarrow{def}}$$は左の書き方は右で定義されるという意味で使っている。

これが理解できると、高校数学で(数研出版の数Ⅰ教科書では)説明なしにただ約束とした「空集合はすべての集合の部分集合である」ということが証明できる。以下にその証明を示す。

空集合$${\empty}$$はすべての集合の部分集合である
[証明]
$${\empty \subseteq B}$$を示す．
つまり, $${\forall x(x \in \empty \to x \in B)}$$を示せばよい．
空集合なので, $${x \notin \empty}$$である．
よって, 前提が偽なので, $${\forall x(x \in \empty \to x \in B)}$$は真である．
したがって, $${\empty \subseteq B}$$である．$${\Box}$$

また、すべての集合$${A}$$は、$${A}$$自身の部分集合であることも証明できる。(問題4)

集合の相等(集合の等価性)

2つの集合$${A, B}$$がすべて同じ要素からなるとき、集合$${A}$$と集合$${B}$$は等しい(相等である)といい、$${A = B}$$と表す。この厳密な定義は以下のようになる。

$${A = B \xLeftrightarrow{def} (A \subseteq B) \land (B \subseteq A)}$$

演習問題2

問題3 次の(a)~(f)のうち、正しいものをすべて選べ。
(a)$${1 \subseteq \{1,2,3\}}$$
(b)$${\{a\} \subseteq \{a,b,c\}}$$
(c)$${\{1,2\} \subseteq \{1,\{1,2\}\}}$$
(d)$${\empty \subseteq \empty}$$
(e)$${\{1,2,3\} = \{2,3,1\}}$$
(f)$${\{1,2,3\} = \{1,\{2,3\}\}}$$

[方針]
部分集合や等しいかどうかはともに左右の集合の要素を比べて考える
[解答]
(b),(d),(e)
(a)は左が集合になっていないので、誤り
(c)は右の集合に$${1,2}$$という要素はない($${\{1,2\}}$$という要素はある)ので、誤り
(f)は右の集合に$${1,2,3}$$という要素はないので、誤り

※(d)の補足として、$${\empty}$$の部分集合は$${\empty}$$のみである。

問題4 すべての集合$${A}$$について、$${A}$$自身が部分集合であることを証明せよ。

[証明]
$${A \subseteq A}$$を示す．
つまり, $${\forall x(x \in A \to x \in A)}$$を示せばよい．
$${x \in A}$$とする．このとき,  $${x \in A}$$である．
よって,  $${\forall x(x \in A \to x \in A)}$$は真である．
したがって, $${A \subseteq A}$$である．$${\Box}$$

問題5 集合$${A=\{a,b,c\}}$$について、部分集合をすべて求めよ。

[解答]
$${\empty, \{a\}, \{b\}, \{c\}, \{a,b\}, \{a,c\}, \{b,c\}, \{a,b,c\}}$$

問題6 集合$${A=\{n|n \in \{1,2,3,…\}\}}$$と集合$${B=\{k-2|k \in \{3,4,5,…\}\}}$$について、$${A=B}$$であることを証明せよ。

[証明]
$${(A \subseteq B) \land (B \subseteq A)}$$を示す．
まず, $${A \subseteq B}$$について, 
$${\forall x(x \in A \to x \in B)}$$を示せばよい．
$${x \in A}$$とする．このとき,  $${\exists n \in \{1,2,3,…\} \space s.t. \space x=n}$$となる．
ここで, $${k=n+2}$$とすると, $${x=k-2}$$となる．
よって, $${x \in B}$$となる．
したがって,  $${\forall x(x \in A \to x \in B)}$$は真である．
次に, $${B \subseteq A}$$について, 
$${\forall x(x \in B \to x \in A)}$$を示せばよい．
$${x \in B}$$とする．このとき,  $${\exists k\in \{3,4,5,…\} s.t. x=k-2}$$となる．
ここで, $${n=k-2}$$とすると, $${x=n}$$となる．
よって, $${x \in A}$$となる．
したがって,  $${\forall x(x \in B \to x \in A)}$$は真である．
以上の議論より, $${A \subseteq B}$$かつ$${B \subseteq A}$$なので, $${A=B}$$である．$${\Box}$$

最後に

今回は、大学数学・集合論の解説記事として、集合どうしの関係について解説しました。今回は、論理記号が多く登場したので、理解していないと難しいかもしれません。また、いくつかの証明についても取り扱いました。この記事の続きとして、集合演算の解説記事を書く予定です。では。

この記事の続きは以下の記事です。