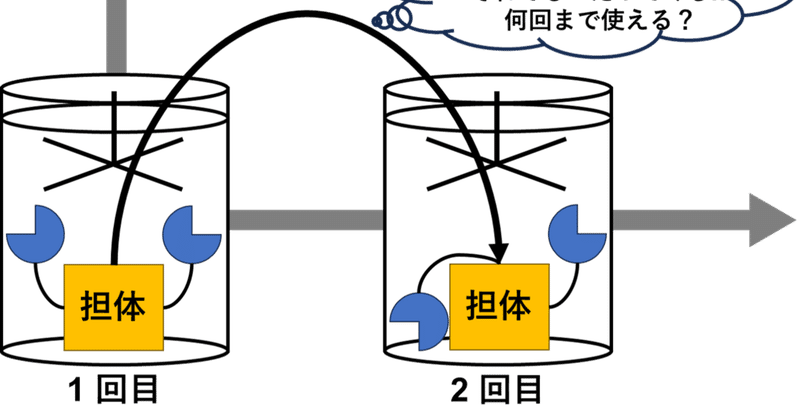
固定化酵素を用いて繰り返し回分反応を行う時,必要な反応時間はどう変化するの?
はじめに
数学得意な方にお伺いしたいんですが,
$${f(x) = \cfrac{Ae^{-Bx}(C-\int^x_0f(x)dx)}{D+(C-\int^x_0f(x)dx)}}$$
($${A, B, C, D}$$ は定数)
って解ける積分方程式ですか?
(後ほど出てきます)
概略
やりたいこと
固定化酵素を用いた回分反応の所要時間が予想できないのをなんとかしたい.たぶん下記二点が絡み合うことが予想のネックになっている.
酵素が触媒する反応の速度が反応の進行に伴い変化する.
酵素そのものが徐々に失活する.
計算方法
まじめにやろうとすると積分方程式になってちょっと大変そう.今回は速度を微小時間に掛ける方法で誤魔化した.
計算結果
半減期の四倍をまたぐ反応はほぼ終了しない,と思う.そこまでに何回反応できるかが勝負っぽい.それ以上の有益な情報は今回の結果だけではわからなかった.
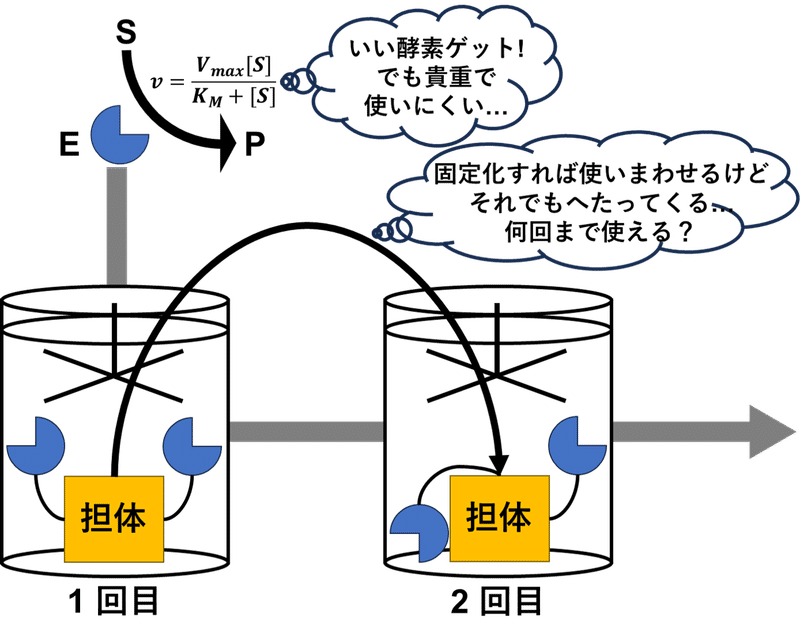
緒論
酵素とは化学反応を触媒するタンパク質であり,一般に通常の金属触媒と比して温和な条件で進行する,位置選択性や立体選択性に優れる,溶媒等を要さず環境に優しいなどの利点がある.このため,食品・医薬品領域で利用に注目が集まっている.タンパク質であるため純度の高いものは高価になりがちであるが,不溶性担体に酵素を固定化することにより,反応終了後に酵素と生成物を容易に分離でき,残った酵素を次の反応に再利用できる.これはなかなかに魅力的である.
しかし実際に固定化酵素を用いて繰り返し回分反応をやってみるとわかるのだが,反応時間の管理が難しい.そもそも酵素反応の速度はもっとも単純な Michaelis-Menten 式であっても非線形な振る舞いであり,ここに連続使用による酵素失活を加味して反応速度の時間変化を見積もる必要があるからである.目的物質の生成量はこの積分値である.今回は一次速度式で失活する固定化酵素を,繰り返し回分反応に供した場合の反応時間を見積もる.
計算方法
真面目に計算しようとすると
酵素 $${E}$$ の失活は一次反応とする.
すなわち,$${[E]_t = [E]_0 e^{-kt}}$$ ($${k}$$ は定数).
ここで $${[X]_t}$$ は時刻 $${t}$$ における化合物 $${X}$$ の濃度.
更にこの酵素が触媒する反応 $${S \rightarrow P}$$ の速度は Michaelis-Menten 式に従うとする.
すなわち時刻 $${t}$$ における反応速度 $${v(t)}$$ は,
$${v(t) = \cfrac{V_{max, t}[S]_t}{K_M+[S]_t}}$$.
この時,$${V_{max, t}\varpropto [E]_{t}}$$ であるから,$${V_{max, t}}$$ は一次速度式にしたがって低下する.
すなわち $${V_{max, t}=V_{max, 0} \times e^{-kt}}$$
$${\therefore v(t)= \cfrac{V_{max, 0} \times e^{-kt}[S]_t}{K_M+[S]_t}}$$
また,時刻 $${t}$$ における基質 $${S}$$ の濃度 $${[S]_t}$$ は初濃度から反応速度の積分値を引いたものなので
$${[S]_t = [S]_0 - \displaystyle\int_0^tv(t)dt}$$
$${\therefore v(t)= \cfrac{V_{max, 0} \times e^{-kt}[S]_t}{K_M+[S]_t}}$$
$${= \cfrac{ V_{max, 0} \times e^{-kt} \times ([S]_0 - \displaystyle\int_0^tv(t)dt)}{K_M+([S]_0 - \displaystyle\int_0^tv(t)dt)}}$$
なんかエグめの積分方程式になっちゃった (冒頭の式).
これ解けるのかな…?
とりあえず誤魔化すと
ちょっと上の積分方程式を解く自信がないので,とりあえず下記のやり方で誤魔化す.
$${v(t)=\cfrac{V_{max, 0} \times e^{-kt}[S]_t}{K_M+[S]_t}}$$
とすると,反応時間を $${\tau}$$ ごとに区切ったとき,$${[S]_{t+ \tau}}$$ と $${[P]_{t+ \tau}}$$ は,
$${[S]_{t+ \tau}=[S]_t-v_t \times \tau}$$
$${[P]_{t + \tau}=[P]_t+v_t \times \tau}$$
とあらわせる.
これを用いて転化率 99% 到達にかかる時間を求めることにする.
計算結果
仮に活性の半減期 24 時間 ($${k=0.0288}$$),$${K_M=1}$$ mM の酵素を $${V_{max, 0}=1}$$ mM / hrとなるように固定化し,$${[S]_0=10}$$ mM の基質溶液に浸漬するとする (今回は $${\tau = 0.1}$$ hr とした).
一時間おきに生成物濃度を測定し $${[P]_t \ge 9.9}$$ mM (収率 $${\ge 99}$$%) の時点で固定化酵素を引き上げ,新しい基質溶液に浸漬することを繰り返すとき,生成物濃度,残存活性,反応速度の推移はそれぞれ下図のようになる.
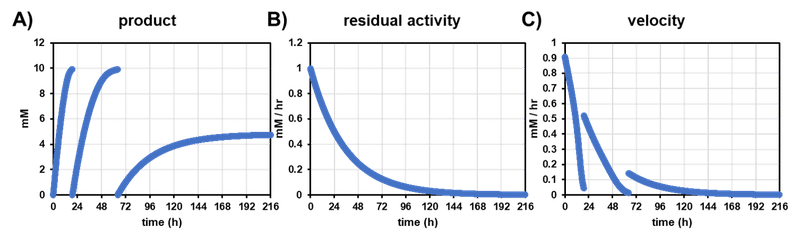
わざわざ酵素を固定化する手間をかけるからには三回くらいは繰り返し使用したいところであるが,この条件では一回目反応は 19 時間で終了するものの,二回目反応には一回目の約 2.4 倍に当たる 45 時間を要し,三回目反応は現実的な時間では終了しないであろうことが見てとれる.
半減期が 24 時間なので 100 時間後には残存活性が約 5% まで低下する.回分反応の場合は基質濃度も低下していくので,更に反応速度は低下する.逆に言うとそれまでに目標の反応を終わらせたいところであり,例えば酵素の固定化量を増やすなどの対策が考えられる.固定化酵素量を二倍にして同様の試験を行った場合は下図のようになる.
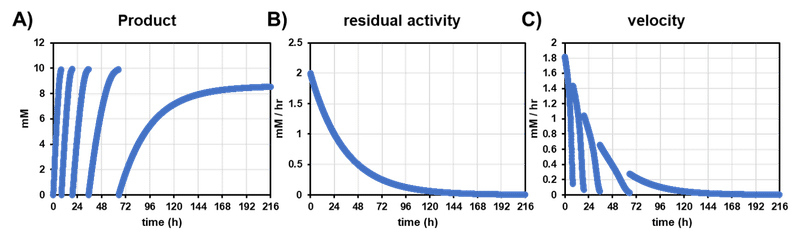
一回目反応は 8 時間,二回目反応は 11 時間と反応時間が短縮できており,四回目反応までは実施することができている.しかしやはり累積反応時間 100 時間をまたぐ五回目反応は終了しなかった.
下図に $${V_{max, 0}=1}$$ or $${2}$$ mM /hr のときの各反応に要する時間を表した.
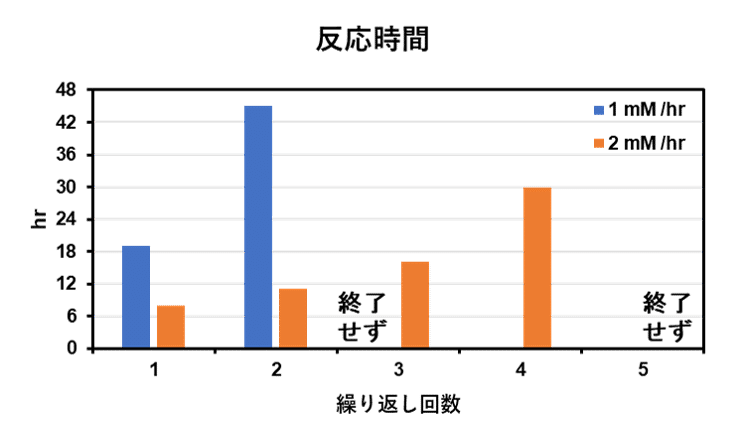
所感
大まかな雰囲気として,半減期の四倍の時間までに終わる反応回数が最大の繰り返し回数になりそうだなというのはつかめた.数学力が低すぎてキチンと解析できなかったので,それ以上の一般的な議論はできない…
積分が得意な方ご助言いただけると本当に助かります.
また今回の検討の懸念点は他に少なくとも下記二点がある.
① 固定化酵素の失活は一次速度式でない可能性が高い.
例えば Ryuichi M. and Shuji A. 2023 は固定化酵素の失活速度が $${A=A_0e^{-kx}}$$ に従わないことを実験的に確認し,これに合う理論を提唱している.
② Michaelis-Menten 式は回分反応では成立しない可能性が高い.
例えば多くの酵素では生成物阻害がかかるが Michaelis-Menten 式ではこれが考慮されていないし,反応の可逆性も無視されている.そもそも目的反応が一基質一生成物反応である可能性も実用的にはかなり低いのではないか.そうなると速度式はさらに複雑になる.
数学的にも酵素学的にも課題山積な結果になってしまったが,とりあえず今日はここまで.
この記事が気に入ったらサポートをしてみませんか?
