数学とコンピュータⅡ advent calendar 2017の記事です。連分数を用いてplain RSA暗号が攻撃できる（Wiener's attack）という定理の概要を説明します。また、Wiener's attackをR言語の関数として実装します。

目次
１．plain RSA暗号とは？
２．Wiener's attackとは？
３．攻撃の要：とても近い値を持つ2つの有理数
４．連分数近似：近い有理数をあぶりだす方法
５．試しにやってみよう
６．公開鍵だけで所望のk/dが得られたか判定する方法
７．Wiener's attackが可能な秘密鍵dの大きさ
８．R言語でWiener's attackの関数を実装しよう

１．plain RSA暗号とは？

plain RSA暗号とは、公開鍵暗号の一種です。公開鍵暗号は他者に公開する公開鍵と他者には秘匿にする秘密鍵からなります。平文を送る側は公開鍵を用いて暗号文を作り、暗号文を読む側は秘密鍵によってこれを平文に復号します。

さて、plain RSA暗号では公開鍵と秘密鍵を次のようにして生成します。
・2つの素数p, qを選ぶ。
・(p-1)(q-1)と互いに素な自然数dを選ぶ。
・deの(p-1)(q-1)で割った余りが1になるような自然数eを見つける。
・dを秘密鍵とし、e, n=pqを公開鍵とする。
（※ d, eは(p-1)(q-1)以下の自然数で選ぶ。）

例えば、2つの素数をp=101, q=641として選ぶ（n=64741）。(p-1)(q-1)=64000なので、例えばd=3を選ぶことができる。3eを64000で割って1余るような自然数eは、e=42667である。d=3を秘密鍵として、(e,n)=(42667,64000)を公開鍵とする。

公開鍵と秘密鍵を生成の仕方は分かったが、どのように使えば暗号化したり復号できたりするのだろうか。平文をM、暗号文をCと書くとすると、
・暗号化：C = M^e mod n（Mをe乗したときのnで割った余り）
・復号：M = C^d mod n（Cをd乗したときのnで割った余り）
とすればよいことが知られている。

例えば、平文M=18を送りたい場合、まず送信者はC = 18^42667 mod 64741によってC = 15969を得る。一方、受信者はM = 15969^3 mod 64741によってM=18と平文を復号することが出来る。

以上の紹介から、plain RSA暗号は公開されているn=p*qが素因数分解されて素数p, qがわかってしまうと、たちまち秘密鍵が分かって誰でも復号できてしまうこととがわかる。（素因数分解可能 ⇒ RSA暗号は解読可能）

２． Wiener's attackとは？

結論から言うと、Wiener's attackとは「公開鍵eが大きすぎると、公開鍵(e,n)から秘密鍵が復元できてしまう。」というものだ。公開鍵eは(p-1)(q-1)以下から選ばれること考えると、実は先の例も秘密鍵がe=42667と大きめだった。このような場合に公開鍵(e,n)=(42667,64741)だけで秘密鍵dが復元できる。

３．攻撃の要：とても近い値をもつ2つの有理数

plain RSA暗号には、値の近い2つの有理数が隠れている。暗号の生成法から、
・de = k(p-1)(q-1)+1（この式を満たすような自然数kが存在する。）
が成り立っていることがわかる。ここで、暗号に使われる素数は基本的に桁が大きいことに注意してほしい。(p-1)(q-1) = pq-p-q+1をよく見ると、n=pqの桁がp, qの桁と比較にならないくらい大きいので、(p-1)(q-1)~nと近似してよいことがわかるだろう。要は、
・de ~ kn
という関係が成り立つ。すなわち公開鍵から計算できるe/nという有理数と、秘密鍵がないとわからないk/dという有理数が実はとても近い値のだ。

４．連分数近似：近い有理数をあぶりだす方法

さて、公開鍵から計算できる有理数e/nと秘密鍵からしか計算できないk/dはとても近い値なのだという話をした。さて有理数e/nからk/dをあぶりだす方法はないだろうか。実はここに連分数が登場する。

連分数とは、次のようなもののことだ。

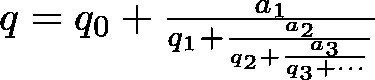
特に今回は、分子がすべて1の連分数を考えることにしよう。実数qに対してこのような連分数表示を[q_0;q_1,q_2,...]と略記して書いたりする。例えば、3/5の連分数表示は

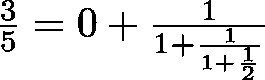
と得ることができ、[0;1,1,2]と略記される。

さて、この連分数表示を途中で打ち切ってみるとどうなるだろうか。（ただし、最後のindexが偶数の時は最後のq_iに1を加えたものを考える。）
・[1] = 1
・[0;1] = 1
・[0;1,2] = 2/3
・[0;1,1,2] = 3/5
どんどん3/5に近くなっている様子がわかるだろうか。このように連分数表示を途中のq_iで打ち切って得られる有理数を「実数qの第i連分数近似」という。実は公開鍵eが十分大きいとき、有理数e/nの連分数近似のなかにk/dが現れるというのがWiener's attackの正体なのだ。

５．試しにやってみよう

先ほどの公開鍵(e,n)=(42667,64741)に対して、Wiener's attackをやってみよう。e/n=42667/64741の連分数表示は[0;1,1,1,13,1,9,1,1,70]と計算できる。
・[1] = 1
・[0;1] = 1
・[0;1,2] = 2/3
・[0;1,1,1] = 2/3
・[0;1,1,1,14] = 29/44
・[0;1,1,1,13,1] = 29/44
・[0;1,1,1,13,1,10] = 317/481
・[0;1,1,1,13,1,9,1] = 317/481
・[0;1,1,1,13,1,9,1,2] = 922/1399
・[0;1,1,1,13,1,9,1,1,70] = 42667/64741
となる。ここで、第２連分数近似の2/3に注目してほしい。
・de = k(p-1)(q-1)+1
だったが、試しにp=101, q=641, e=42667を用いて、k/d=2/3（k=2, d=3）としてこの等式が成り立つか確認すると
・de = 3*42667 =128001, k(p-1)(q-1)+1 = 2*64000+1 = 128001
左辺と右辺の値がぴったり一致しているではないか。実際、秘密鍵はd=3（連分数近似の値2/3の分母そのもの）だった。確かに有理数e/nの連分数近似のなかにk/dが存在していたわけだ。

６．公開鍵だけで所望のk/dが得られたか判定する方法

公開鍵から計算できる有理数e/nの連分数近似はいっぱいある。これらのうち、どれがk/dなのかが公開鍵のみから判定できないとplain RSA暗号の秘密鍵dが分かったとは言い難い。しかし、これには良い方法がある。すべての鍵は２次方程式だ！

秘密鍵dとkがもしわかっているとすると、de = k(p-1)(q-1)+1から(p-1)(q-1)を得ることができる。実は、(p-1)(q-1)とpqが分かっていると容易にp,qがわかる方法があるのだ。（p,qが分かれば、n=pqかをチェックすればよい。）

２次方程式x^2-ax+b=0の解がp,qだったとき、解と係数の関係
・a = p+q
・b = pq
というのがあった。しかし、a = p+q = pq-(p-1)(q-1)+1だし、b = nである。どちらも直ちに計算できる。あとは２次方程式の解の公式を使えば、素数p, qが得られるわけだ。２次方程式の解の公式は、素因数分解と違い公式に当てはめるだけで、とても計算量が小さい。

７．Wiener's attackが可能な秘密鍵dの大きさ

実は公開鍵eが大きくなると、秘密鍵dは小さくなる。Wiener's attackを使えば、秘密鍵dが(1/3)*(nの4乗根)以下の場合は必ずplain RSA暗号を攻撃できることが証明されている。裏を返せば、plain RSA暗号の秘密鍵はこの値より必ず大きく生成せねばならない。（実際、先ほどの例は(1/3)*(nの4乗根) ~ 5.32だった。それゆえ秘密鍵d=3はWiener's attackで復元できてしまったのだ。）

８．R言語でWiener's attackの関数を実装しよう

R script：

wiener_attack <- function(e,n){
　# e/nの連分数表示を得る。
　cont_frac <- 0
　x <- e; y <- n # x：分子, y:分母
　repeat{
　　q_i <- floor(y/x)
　　if(x!=0){
　　　cont_frac <- c(cont_frac, q_i)
　　　tmp <- x
　　　x <- y-q_i*x
　　　y <- tmp
　　}else{
　　　break
　　}
　}
　# k/dを求める。（連分数近似）
　i <- 1
　repeat{
　　array <- cont_frac[1:(i+1)]
　　if(i%%2==0){
　　　array[(i+1)] <- array[(i+1)]+1
　　}
　　k <- 1; d <- array[(i+1)]
　　for(j in i:1){
　　　tmp <- k
　　　k <- d# 分子
　　　d <- array[j]*d+tmp# 分母
　　}
　　tmp <- k
　　k <- d
　　d <- tmp
　　tmp <- c(k,d)
　　# print(c(i,tmp)) # debug用に連分数近似をprint
　　if(k==e&d==n){
　　　print("Wiener's attack failed...")
　　　break
　　}
　　# 得られた値がk/dかを調べる。
　　a <- -(n-(e*d-1)/k+1)
　　b <- n
　　if((e*d-1)%%k==0 & a^2-4*b>0){
　　　p <- (-a+sqrt(a^2-4*b))/2
　　　q <- (-a-sqrt(a^2-4*b))/2
　　　if(floor(p)==p){
　　　　res <- c(d,p,q)
　　　　names(res) <- c("d","p","q")
　　　　print(res)
　　　　break
　　　}else{
　　　　 i<-i+1
　　　}
　　}else{
　　　i <- i+1
　　}
　}
}

実行例：
> wiener_attack(42667,64741)    # Wiener's attackが成功する例
d p q
3 641 101    # 秘密鍵d = 3, 鍵生成に使用した素数(p,q)=(641,101)
> wiener_attack(103,143)     # Wiener's attackが成功しない例
[1] "Wiener's attack failed..."