＜タイル張り＞
同じ形、大きさの図形で隙間なく平面を埋め尽くすことは、古代ギリシャ時代から「タイル張り」の問題として研究されてきた。
そして、正多角形で平面を「隙間なく埋め尽くすこと」（以後「充填」とする）ができるのは、正三角形、正四角形、正六角形の３種のみであることが明らかになる。

理由は簡単で、正三角形の一つの内角は、「60」度であり、正四角形、正五角形、正六角形の一つの内角は「90,108,120」である。そうすると、正三角形の一つの頂点には６個の正三角形が集まると「360」度になり、正四角形の場合は４個で「360」になり、正六角形の場合は３個で「360」度になるからである。

＜正五角形は平面充填しない＞
そして、正五角形の場合は３個で「324」度であり、４個では「360」度を超えてしまう。したがって、正五角形は平面を充填することはできないことが分かる。

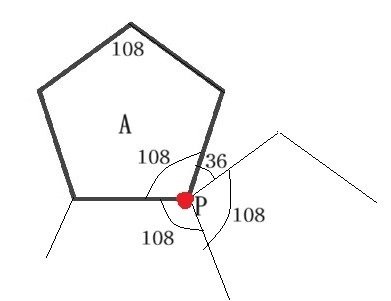
＜正五角形を含む図形＞
正多角形を「平面が充填できるか」どうかで区別するだけでは勿体ない。特に、正五角形については、もう少し調べてみたい誘惑にかられる。
正五角形が内接する長方形を考える。長方形はもちろん「平面充填」する。すると、長方形に内接する正五角形の「充填率」はどれくらいになるのか？を考えてみたい。

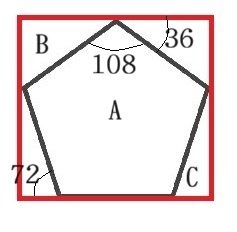
それで、「充填率」を面積の割合と定義して計算をしてみる。
上図のような「一辺の長さが『１』の正五角形」が内接する長方形の縦の長さは「sin(72) + sin(36)≒1.538」である。そして、横の長さは「2cos(36)≒1.618」である。したがって、長方形の面積は約
「2.488」となる。
　もちろん、正五角形の面積は約「1.720」と長方形の面積より小さい。その割合は約「0.69」である。

＜充填率を高くする方法＞
　この割合は、正五角形の周りにある４個の三角形を加えた長方形との比較から出た値である。
　それで、正五角形は「平面充填」はできないけれど、正五角形にできるだけ面積の小さい図形を加えて「平面充填」する道を探りたい。そうすることで、この「充填率」はもっと高くなるはずである。

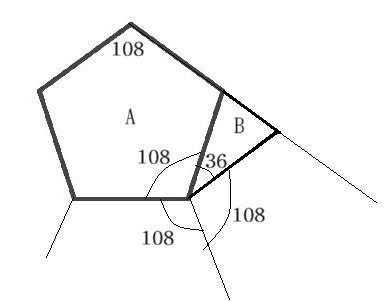
　その一つの試行が上図である。正五角形Ａに三角形Ｂを加えるのである。そうすると、４辺の長さが等しい五角形になる。

　実はこの五角形は「平面充填」するのである。（２個、３個と並べた様子を想像していただきたい。）

　そうすると、三角形Ｂの面積は約「0.2938」であり、Ａ＋Ｂの面積は約「2.0143」であるから、正五角形の平面「充填率」は約「0.85」となる。

＜平面充填できる五角形の探索＞
　この試行での恵みは、「充填率」ばかりではなく、平面を充填できる五角形の発見である。「108,108,108,144, 72」という角度をもつ五角形は平面充填できるのである。
　また、この五角形の辺の長さは「1, 1, 1, 1,  1.618・・・」であり、辺の長さを変えずに角度を変えて変形できる。
　さらに、辺の長さと角度を変えれば平面充填できる五角形が発見できる可能性を示してくれる。

凸五角形で平面充填できるのは一種類だけではない。２０１５年現在で平面充填できる凸五角形は「十五のタイプ」が発見されている。同じタイプであっても角度が異なる五角形もあれば、一つの五角形が複数のタイプに属することもある。

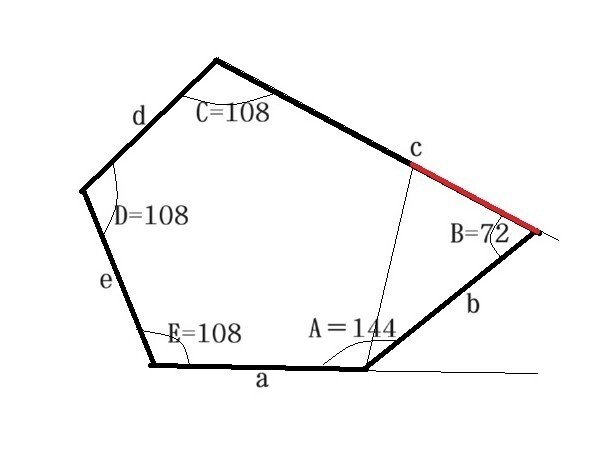
私が発見した五角形のタイプは「B+C=180, A+D+E=360」と表現されるタイプに属している。
そして、辺ｂと辺ｄが平行で正五角形を含む証のように４辺の長さが等しい。

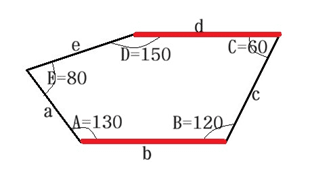
この条件を満たす五角形は他にもたくさん存在する。
一つの例を上に示しておく。
この例では、辺ｂと辺ｄは平行であると同時に長さが等しい図形になっている。
　なお、角Ａ、Ｄ、Ｅの大きさには自由度があり、必ずしも「A=130」でなくてよい。

＜課題はのこる＞
平面充填する凸五角形の探索はまだ終了してはいない。
１９７６年と１９７７年には、アマチュア数学者である主婦マージョリー・ライスが４種類のタイプを発見したという。
その後に、数種類のタイプが発見されて合計で「十五のタイプ」が発見されたことになる。

また、２０１７年に、リヨン高等師範学校のミカエル・ラオは、発見されている「十五のタイプ」以外には、平面充填する五角形は存在しない、という論文を発表したという。
しかし、この論文の真偽については公表されていないようである。

正五角形の「充填度」に話題を戻すことにする。正五角形にできるだけ小さい面積の部品を付属させて「平面充填」できる図形を作ることができるか？という方針で探ってみたのである。

その結果、４個の三角形を付属させて正方形にすると、充填率は約「0.69」であり、１個の三角形を付属させて五角形にすると、充填率は約「0.85」に上昇したのである。この値が最大値なのかどうか。
（どなたか教えて欲しい。）

＜円の平面充填率は・・・＞
さて、正ｎ角形のｎが「６」より大きくなると平面充填は不可能であることは明らかである。（一つの内角が「360」の約数になることはないからである。）
そのｎの値を極限まで大きくした図形が「円」だとすれば当然のことで、「円は平面充填」できない。
それなら、「充填率」はいくらになるのか？

円を規則的に並べる方法は二種類である。「充填率」が大きくなるのは「ズラス方」であることは明らかである。
ちなみに、円に外接する正方形は平面充填できるので、その場合の充填率は「(π/4)≒0.79」である。

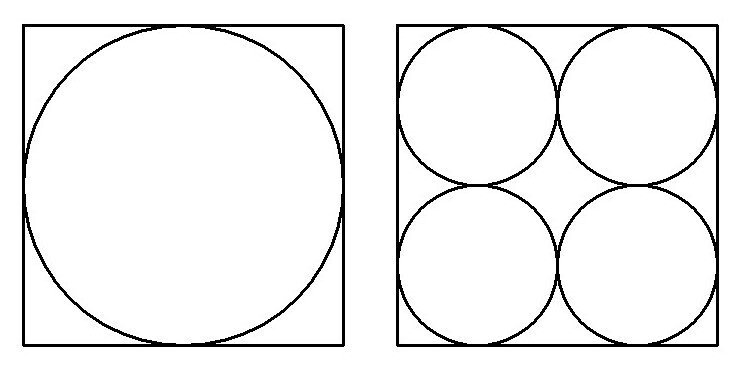
「ズラス方」の充填率は円に湾曲した小さい三角形を付属させた図形を用いて求めることができる。（この図形は平面充填できるからである。）

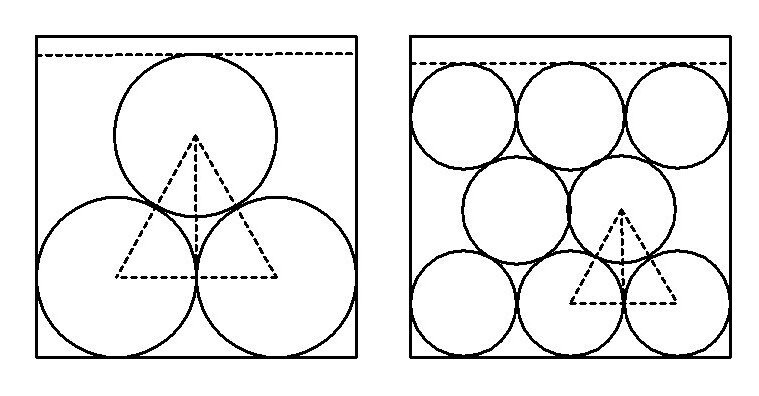
一辺が「２」の正三角形の中に、「１／６」の円が三個と湾曲した三角形が一個含まれる。
それで、湾曲した三角形の面積を求めると次のような計算になる。
　　→√(3 )– (π/2)≒0.16

それで、平面充填できる図形を作る時に、円に小さい湾曲した三角形を何個付属させることが必要になるのか？
一個の場合はスキマができることが分かる。
二個の場合は、次図のようにスキマなく連続して敷き詰めることができる。

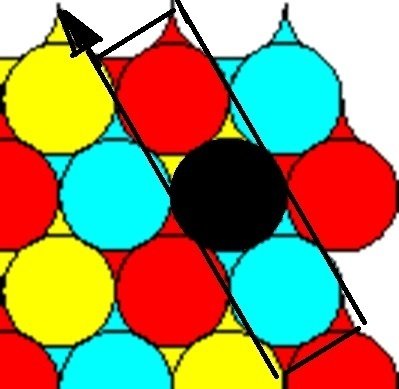
　それで、円の平面充填率は次のようになる。
→　π÷［π＋2×(√3−(π/2))］
　＝π÷2√3≒0.906

「π≒3.14」とこれまでの数字を用いると「3.14÷（0.16×2+3.14）であり、約「0.907」となる。

＜ガウスがめざしたもの＞
この平面充填率の値はガウス（１７７７～１８５５）も求めていたという。

ガウスが目指していたのは、１６１１年に天文学者でもあるケプラーが予想したという「球による空間充填率」を求めることであった。
そして、ガウスは「円による平面充填率」ばかりではなく、１８３１年には「球による空間充填率」として「(π/3√2)≒0.74」を求める。

この値については、１９９８年にトーマス・ヘイルズがコンピュータを用いて最大値であることを証明したという。