どうも、108Hassiumです。

去年の9月から始めたnoteの週1更新は1周年を迎え、記事数は今回で55本目になります。

55といえばフィボナッチ数なので、この記事ではフィボナッチ数の話をします。

123456789番目のフィボナッチ数を4で割った余りは？

タイトルの問題を解いてみます。

まず、フィボナッチ数列を$${m}$$で割った余りを$${F_m(n)}$$と略記することにします。

$${F(n+2)}$$を4で割った余りは$${F(n+1)}$$を4で割った余りと$${F(n)}$$を4で割った余りの組み合わせで決まるので、$${F_4(n)}$$と$${F_4(n+1)}$$のペアを順番に並べてみます。

• $${(F_4(0),F_4(1))=(0,1)}$$

• $${(F_4(1),F_4(2))=(1,1)}$$

• $${(F_4(2),F_4(3))=(1,2)}$$

• $${(F_4(3),F_4(4))=(2,3)}$$

• $${(F_4(4),F_4(5))=(3,1)}$$

• $${(F_4(5),F_4(6))=(1,0)}$$

• $${(F_4(6),F_4(7))=(0,1)}$$

初期値と同じ(0,1)という組み合わせになったので、$${F_4(n)}$$は「0,1,1,2,3,1」という列が繰り返される6周期の周期数列になることがわかります。

$${F_4(n)}$$が6周期ということは、$${n}$$を6で割った余りを求めることで$${F_4(n)}$$を計算できることになります。

123456789を6で割った余りは3なので、123456789番目のフィボナッチ数を4で割った余りは$${F_4(3)}$$と等しく、その値は2になります。

ところで、この問題を4以外の数で割った余りに拡張したらどうなるのでしょうか？

例えば10で割った余り(=1の位)を求める場合、難易度はどう変化するでしょうか？

この場合も先程と同じように$${F_{10}(n)}$$の周期を調べればよいのですが、どうやら$${F_m(n)}$$の周期には「Pisano period」という名前が付いており、wikipediaに専用ページがある(ただし日本語版はない)くらい有名な概念らしいです。

$${F_m(n)}$$の周期は$${\pi(m)}$$(円周率とは特に関係ないらしいです)と表記され、wikipediaいわく$${\pi(10)=60}$$らしいです。

123456789=60×2057613+9なので、$${F_{10}(123456789)=F_{10}(9)=4}$$となります。

F(F(F(F(123))))を33で割った余りは？

ここまでの話は、フィボナッチ数の周期とpisano periodを紹介するためだけの導入部です。

ここからは、私が昔発見したフィボナッチ数に関する奇妙な性質の話をします。(先行研究例はほとんど調べていません)

まず、pisano periodは以下のようなコードで計算できます。

void setup(){
  println(p(10));
}

int p(int m){
  int f,pf,ppf,a;
  pf=1;
  f=1;
  for(a=1;!(pf==0&&f==1);a++){
    ppf=pf;
    pf=f;
    f=(pf+ppf)%m;
  }
  return a;
}

※言語はProcessing
※p(1)の値は正常に計算できません

これを実行すると、例として$${\pi(10)}$$の値である60が出力されます。

さて、$${F(F(F(F(123)))}$$を33で割った余りは以下のような手順で計算できます。

まず、$${\pi(33)=40}$$なので$${F(F(F(F(n))))}$$を33で割った余りを求めるには$${F(F(F(n)))}$$を40で割った余りを求めればいいことがわかります。

次に、$${\pi(40)=60}$$なので$${F(F(F(n)))}$$を40で割った余りを求めるには$${F(F(n))}$$を60で割った余りを求めればいいことがわかります。

次に、$${\pi(60)=120}$$なので$${F(F(n))}$$を60で割った余りを求めるには$${F(n)}$$を120で割った余りを求めればいいことがわかります。

次に、$${\pi(120)=120}$$なので$${F(n)}$$を120で割った余りを求めるには$${n}$$を120で割った余りを求めればいいことがわかります。

以上より、

$${F_{33}(F(F(F(123))))\\=F_{33}(F_{40}(F_{60}(F_{120}(123))))\\=F_{33}(F_{40}(F_{60}(3)))\\=F_{33}(F_{40}(2))\\=F_{33}(1)\\=1}$$

と計算できます。

ところで、計算途中で出てきた40、60、120という値は$${\pi(33)}$$、$${\pi(\pi(33))}$$、$${\pi(\pi(\pi(33)))}$$に対応しており、数列として表すと

$${\begin{cases}a_0=33\\a_{n+1}=\pi(a_n)\end{cases}}$$

…という漸化式で表せます。

この数列は$${a_3=a_4=120}$$なので、その先もずっと120だけが並びます。

さて、初期値を変えてこの数列を計算すると以下のようになります。

• 1→1

• 2→3→8→12→24→24

• 3→8→12→24→24

• 4→6→24→24

• 5→20→60→120→120

• 6→24→24

• 7→16→24→24

• 8→12→24→24

• 9→24→24

• 10→60→120→120

どうやらこれ以外の初期値でも、$${a_n}$$は何らかの値に収束していくようでした。

ちなみに、50万以下の自然数のうち$${n=\pi(n)}$$が成り立つのは以下の7個でした。

• 1

• 24

• 120

• 600

• 3000

• 15000

• 75000

• 375000

ところで、「ある数列が初期値によらず一定の結果に収束していくか」を問う問題と言えばコラッツ予想が有名です。

コラッツ予想といえば1に辿り着くまでの項数が初期値によって大きく異なるのが有名(多分)ですが、$${a_n}$$が不動点に辿り着くまでの項数はコラッツ数列ほど激しくは変動しないようです。

以下、$${a_0=n}$$としたときに$${a_{m}=a_{m+1}}$$になるような最小の$${m}$$を$${\rho(m)}$$とします。

50万以下の初期値で$${\rho(m)}$$の最大値が更新されるような$${m}$$を調べてみたところ、以下のようになりました。

• $${\rho(2)=4}$$

• $${\rho(127)=6}$$

• $${\rho(509)=7}$$

• $${\rho(1019)=8}$$

• $${\rho(2039)=9}$$

• $${\rho(4079)=10}$$

• $${\rho(16384)=11}$$

• $${\rho(32768)=12}$$

• $${\rho(65536)=13}$$

• $${\rho(131072)=14}$$

• $${\rho(262144)=15}$$

よく見ると、7行目からは左辺の引数が全て2の冪乗になっています。

16384より小さい2の冪乗に対しても$${\rho(n)}$$を計算してみました。

• $${\rho(2)=4}$$

• $${\rho(4)=2}$$

• $${\rho(8)=2}$$

• $${\rho(16)=1}$$

• $${\rho(32)=2}$$

• $${\rho(64)=3}$$

• $${\rho(128)=4}$$

• $${\rho(256)=5}$$

• $${\rho(512)=6}$$

• $${\rho(1024)=7}$$

• $${\rho(2048)=8}$$

• $${\rho(4096)=9}$$

• $${\rho(8192)=10}$$

最初の3つは不規則ですが、それ以降は1ずつ増えていっています。

もし疑問3-2が肯定的に解決されれば、自動的に疑問3-1も解決されます。

ちなみにコラッツ数列の方でも似たような性質があって、2の冪乗を初期値にすると指数の値を1増やすごとに1に辿り着くまでの項数が1ずつ増えていくのですが、そっちの性質は定義からほとんど明らかなので疑問3-3ほどは面白くはないです。

あとこれも余談なのですが、2の冪乗が出てくる前の2、127、509、1019、2039、4079、という値のうち、最初の2つを除いた4つの値は以下のように表せます。

$${509=512-3=2^9-2^1-1}$$
$${1019=1024-5=2^{10}-2^2-1}$$
$${2039=2048-9=2^{11}-2^3-1}$$
$${4079=4096-17=2^{12}-2^4-1}$$

じゃあ$${\rho(2^{n+8}-2^n-1)=n+6}$$が成り立つんじゃないか、と思ったのですが残念ながら$${\rho(2^{13}-2^5-1)=3}$$となり成り立ちませんでした。

L(L(L(L(123))))を33で割った余りは？

以下の数列の項を、リュカ数と呼びます。

$${\begin{cases}L(0)=2\\L(1)=1\\L(n+2)=L(n+1)+L(n)\end{cases}}$$

※フィボナッチ数列とは異なり、数列そのものをリュカ数列とは呼ばないようです。

また、リュカ数の列を$${n}$$で割った余りの周期を$${\pi_L(n)}$$と書くことにします。

$${\pi_L(n)}$$の値は$${n}$$によっては$${\pi(n)}$$と異なる値になり、$${\pi(n)\neq\pi_L(n)}$$となる最初の10個の$${n}$$とそのときの$${\pi(n)}$$、$${\pi_L(n)}$$の値は以下のようになります。

パッと見でわかる通り、$${n}$$の値は全て5の倍数になっています。

どうやらこれは既知の性質らしく、OEISのコメント欄に載っています。

さて、5の倍数のときに周期が変わるということは$${L(L(L(L(123))))}$$を33で割った余りの計算は、フィボナッチ数のときとは途中から違った道を進むことになりそうです。

$${\pi_L(33)=40}$$で、$${\pi_L(\pi_L(33))}$$の値は60ではなく12になり、$${\pi_L(\pi_L(\pi_L(33)))=24}$$、$${\pi_L(\pi_L(\pi_L(\pi_L(33))))=24}$$になります。

123を24で割った余りは3、$${L(123)}$$を24で割った余りは3、$${L(L(123))}$$を12で割った余りは3、$${L(L(L(123)))}$$を40で割った余りは3となり、$${L(L(L(L(123))))}$$を33で割った余りは3であることがわかります。

以下、フィボナッチ数に対する$${a_n}$$と同様に、数列$${b_n}$$を$${b_{n+1}=\pi_L(b_n)}$$と定義します。

$${a_n}$$はたくさん(おそらく無限個)の不動点を持っていましたが、$${b_n}$$の方は50万以下では不動点は2個しか見つかりませんでした。

ところで、リュカ数はフィボナッチ数の定義における初期値の組み合わせを変えただけのものですが、リュカ数以外にも初期値を変えただけの数列を作ることはできます。

そういった数列を$${n}$$で割った余りの周期は、どうなるのでしょうか？

初期値の組み合わせは無限に存在しますが、初期値を$${n}$$で割った余りの組み合わせは$${n^2}$$通りしかないのでループの個数は有限個のはずです。

というわけで、プログラムを書いて調べてみました。

void setup(){
  int x,px,ppx,n=0;
  int[][] list=new int[10][10];
  for(int a=0;a<10;a++){
    for(int b=0;b<10;b++){
      list[a][b]=0;
    }
  }
  for(int a=0;a<10;a++){
    for(int b=0;b<10;b++){
      if(list[a][b]==0){
        n++;
        px=a;
        x=b;
        print(a+",");
        for(int c=0;!(0<c&&px==a&&x==b);c++){
          print(x+",");
          ppx=px;
          px=x;
          x=(px+ppx)%10;
          list[px][x]=n;
        }
        println();
      }
    }
  }
  println("loop;"+n);
}

フィボナッチ数の初期値を変えた数列を10で割った余りのループを全列挙するプログラムです。

実行結果は以下の通りです。

0,0,
0,1,1,2,3,5,8,3,1,4,5,9,4,3,7,0,7,7,4,1,5,6,1,7,8,5,3,8,1,9,0,9,9,8,7,5,2,7,9,6,5,1,6,7,3,0,3,3,6,9,5,4,9,3,2,5,7,2,9,1,0,
0,2,2,4,6,0,6,6,2,8,0,8,8,6,4,0,4,4,8,2,0,
0,5,5,0,
1,3,4,7,1,8,9,7,6,3,9,2,1,
2,6,8,4,2,
loop;6

2行目の長い数列が通常のフィボナッチ数列を10で割った余りの60周期の数列で、それ以外にも20、3、12、4周期のループが存在し、合計で6つのループが存在するようです。

プログラムを少し書き換えて、結果を画像で出力するようにしてみました。

横軸が0番目、縦軸が1番目の初期値を10で割った余りを表し、同じループに含まれる値が同じ色で塗られています。

割る数を変えてみるとこんな感じになります。

サイズを大きくしてあまり面白い模様にはならなさそうだ、と思っていたのですが、一つだけ明らかに異質なものを発見しました。

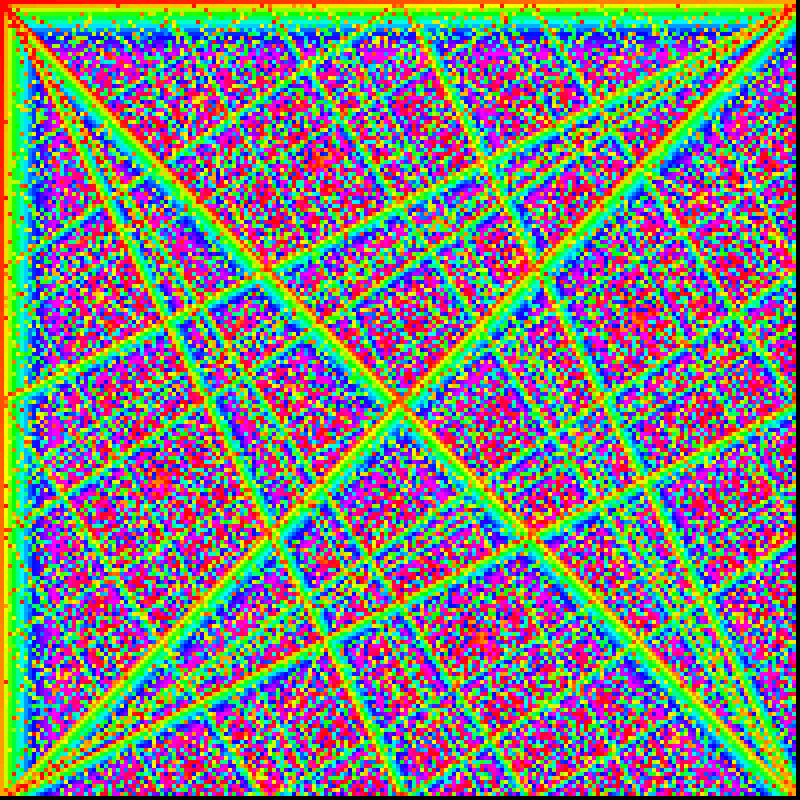
これだけやたらはっきりと線状の模様になっています。

P(P(P(P(123))))を33で割った余りは？

以下の数列の項を、ペル数と呼びます。

$${\begin{cases}P(0)=0\\P(1)=1\\P(n+2)=2P(n+1)+P(n)\end{cases}}$$

また、ペル数を$${n}$$で割った余りの周期を$${\pi_P(n)}$$と表記することにします。

$${\pi_P(33)=24}$$、$${\pi_P(\pi_P(33))=8}$$、$${\pi_P(\pi_P(\pi_P(33)))=8}$$で、123を8で割った余りは3、$${P(123)}$$を8で割った余りは5、$${P(P(123))}$$を8で割った余りは5、$${P(P(P(123)))}$$を24で割った余りは5、よって$${P(P(P(P(123))))}$$を33で割った余りは29になります。

$${n=\pi_P(n)}$$が成り立つ$${n}$$を計算してみたところ、2、4、8、16、32・・・と2の冪乗が出てきました。

ところで、フィボナッチ数、リュカ数、ペル数の列はどれも「リュカ数列」という数列のグループに属しています。

リュカ数列は2つの整数$${p,q}$$を用いて以下のように定義される2つの数列です。

$${\begin{cases}U_{p,q}(0)=0\\U_{p,q}(1)=1\\U_{p,q}(n+2)=pU_{p,q}(n+1)-qU_{p,q}(n)\end{cases}}$$

$${\begin{cases}V_{p,q}(0)=2\\V_{p,q}(1)=p\\V_{p,q}(n+2)=pV_{p,q}(n+1)-qV_{p,q}(n)\end{cases}}$$

※ここまでの記事での表記に合わせて、wikipediaに載っている定義とは異なる記法を使っています。

リュカ数列に対してもこれまでと同様に「$${n}$$で割った余りの周期」と「$${n}$$で割った余りの周期を反復計算した数列」を定義できるので、それぞれ以下のように定義します。

• $${U_{p,q}(n)}$$を$${m}$$で割った余りの数列の周期を$${\pi_{U_{p,q}}(m)}$$とする。

• $${V_{p,q}(n)}$$を$${m}$$で割った余りの数列の周期を$${\pi_{V_{p,q}}(m)}$$とする。

• $${A_{p,q}(n+1)=\pi_{U_{p,q}}(A_{p,q}(n))}$$

• $${B_{p,q}(n+1)=\pi_{U_{p,q}}(B_{p,q}(n))}$$

$${A_{p,q}(n)}$$か$${B_{p,q}(n)}$$が無限大に発散するような$${p,q}$$は今のところ自力では見つけられていませんが、2周期ループなら$${A_{3,-1}(n)}$$での2→3→2等の例が見つかっています。(3周期以上になる例は未発見です)

疑問6-3はそもそも問題としてはかなり曖昧ですが、$${A_{3,-1}(n)}$$はフィボナッチ数のときよりも若干収束が遅いような初期値が多い気がします。

これは余談ですが、フィボナッチ数列を拡張した数列の一種として、リュカ数とは別にトリボナッチ数列というものも存在します。

$${\begin{cases}T(0)=0\\T(1)=0\\T(2)=1\\T(n+3)=T(n+2)+T(n+1)+T(n)\end{cases}}$$

トリボナッチ数列についても余りの周期$${\pi_T(n)}$$やその反復計算について調べてみたのですが、どうやら$${\pi_T(\pi_T(\pi_T(…\pi_T(n)…)))}$$はほとんどの$${n}$$で無限大に発散してしまうようでした。

元々はこの記事で「T(T(T(T(123))))を33で割った余りは？」という問題にも触れようとしたのですが、計算できなかったので諦めました。

おまけ

フィボナッチ数列を反復計算する話が出たので、フィボナッチ数列の一般項を複素数に拡張してフラクタル図形を描画してみました。

要するに$${\frac{\phi^z-(1-\phi)^z}{\sqrt{5}}}$$のジュリア集合です。

なお、$${(1-\phi)^z}$$の部分は

$${(1-\phi)^z\\=e^{z\text{ln}(1-\phi)}\\=e^{z(\text{ln}(-1)+\text{ln}(\phi-1))}\\=e^{z(i\pi+\text{ln}(\phi-1))}}$$

・・・というように変形して計算しました。

しかし$${\text{ln}(-1)}$$という値は本来一通りには定まらないものなので、$${\text{ln}(-1)}$$の値を変えたものも描画してみました。