放物線、あるいは２次関数

タカシくんは八百屋になってりんごを売りました。

毎年売り上げは落ちて行きました。

来年には何個売れるでしょう？

　　　　＊　　　　　　　　　　　　＊　　　　　　　　　　　　＊

前回は、予測の中でもまだまだ簡単でだれでも分かる、「ひたすらまっすぐ」というものの予測の話であった。たとえば宝物が、今日に至るまでに

地点１、地点２、地点３、地点４、地点５、…

という具合に移動してきた事実があるとする。「ならば明日は６の地点にあるだろう」とは、小学生でも考えつくことだろう。

もう少し目で追える速さにしてみよう。速さとは、小学生は「距離 ÷ 時間」と習うが、もう少しだけ正確にすると「単位時間あたりの移動距離」ということになる。

床の上でボールを転がすのをイメージすると分かりやすいかと思われる。そのボールを取ろうとするならば、後ろから追いかけるよりは「このペースだと次にはここに来るな」と思って待ち構えるほうがやりやすいだろう。このとき我々はボールの動きを予測している。計算式を使わなくったっていい。計算と同じことを感覚的にやっている。

ここまでが前回の話だ。

今回はもう少しだけ複雑になる。

高い塔の上から手に持っていたボールを手放した。この場合、ボールは真下に落ちていく。今回はボールの移動距離を考える前に、まずはスピードを測ろう。

１秒後には、かなりざっくりした数字で表すが、秒速約１０mになった。速い。短距離選手並みだ。２秒後には秒速約２０mだった。３秒後は？そう、秒速約３０mだ。

なんのことはない、ここにも比例の関係がある。前回は時間と移動距離に比例関係があったが、今回は時間（秒数）と速度（ここでは秒速で示した）の関係が比例だ。

では前回のように、時間と移動距離の関係を調べるとどうなる？何秒後にボールは、何m下にある？

これもかなりざっくりした数字で表すが、ボールは最初の１秒間で約５m下に落ちる。では次の１秒ではその２倍で１０m下まで落ちているかというとこれがそうではない。２０m下にいる。３秒後には最初の位置からざっくり４５m下にいる。移動距離は比例よりもずっと速い勢いで大きくなっていく。

球技をやる人はこういったボールのコンマ数秒の動きを体で掴んでいる。ボールの動きを予測する、あるいはうまくコントロールする必要があるからだ。計算式を使わなくてもその軌道を把握できている。ただ落ちるボールだけではない。投げ上げられたボールの軌跡だって判る。

例えばバスケットボールだと、

「この角度でこのくらいの勢いで投げれば、こんな風にボールが飛んで行ってゴールに入るはずだ」

と、ボールの軌道を予測してゴールする。私はスカッシュをするが、壁から跳ね返ってきた後のボールが床にぶつかるまでの間の軌道は、簡単に予測できる。

「ボールはこの地点に落ちてくるはずだ！」

という予測ができるからそこに向かって行き、ラケットを当てる。野球ならキャッチボールでボールを取るときも、フライをキャッチするときも、同様の予想をする。逃げる動物を追うよりははるかに簡単な予想で済む。

投げ上げられた物体の描く軌跡を放物線と言う。真上や真下に投げたり落としたりするのではない限り、その道筋はまっすぐではなく曲がっている。

スポーツをせずとも放物線に親しむ方法はある。『アングリーバード』をやったことがあるだろうか？パチンコで鳥を飛ばすゲームだ。あれは放物線を予測するゲームと言ってもいい。初心者用に補助線を示してくれるモードを使うと、放物線の軌道を感覚的に覚えられる。ゲームばかりか現実のパチンコや、バスケットボールのゴールがうまくなる可能性だってある。

放物線は中学校で習う「２次関数」と呼ばれるものと同じ形のカーブになる。地球上では空気抵抗があるので、放物線は厳密には２次関数からずれる。ややこしくなるので、今はそのような細かい誤差は無視しよう。

2次関数の例

２次関数を描くものの例をあげてみる。

1. 「タカシくんは秒速５０mで走らせていた自動車のブレーキを踏んだ。ブレーキを踏み始めた地点から測って、１秒後には４５m先に、２秒後には８０m先に、３秒後には１０５m先にいた。

2.「『１、４、９、１６、…』次の数字は？」
１×１、２×２、３×３、４×４となっていることに気づけば、次は ５×５＝２５だと分かるだろう。

3.本物のパラボラアンテナは二次関数の曲線を描いている。

１.については、どんどん速くなるというのではなく、どんどん遅くなるというだけで、ボールを下に落とすのと本質的な違いはないと考えてよい。（ただ、ブレーキなので止まった後車が後ろにいくことはないから、５秒後には１２５m先でスピードがゼロになって止まったままとなる。グラフもそのまま平らになってしまう）

2.は数字の列、数学では数列と呼ばれるものだ。この数列については「１列目は高さ１の位置に、２列目は４の位置に、３列目は９の位置に・・・」といった具合に点を打ってグラフを描くと、各点は放物線のカーブの上に乗る。

出題者がこの後でたらめを言うと予測はできないが（数学的にも次が２５以外の数字になるような数列を、数式を使って作れる）、ここは素直に「かける数字が１つずつ上がる」とした場合、次の数字だけではなく、１つ飛ばしたその次の数字も、そのまた次の数字も予測できる。なんとなればその先の何番目の数字であろうと、無限に予測できてしまう。

例えば１００番目の数字は、１００×１００で１００００だ。

3.については、電波を集めるのに２次関数の形が利用できるので、そのように人間が作ったというだけである。予測の話ではない。（ただし、パラボラアンテナもどきもあるので、その場合は放物線にはならないが）

予測を計算で出すには数式が必要だ。時間を  t とし、予測したいものの場所（位相）を x とする。x を t の関数としてあらわすことができれば予測は可能だ。

前回の予測では　y ＝ ax　という関数、比例を使った。今回の式はそれとは異なる。２次関数は

y ＝ at^2

となる。"t^2"をひとまとめに見ると「yはtの２乗に比例する」なんて言いかたもできる。

この式を簡単にするために、 a に１を入れると

y = t^2

となる。noteでは数式は書きづらく、２乗は右上に小さく２と書くのでなく^2 となってしまうので読みづらい。ちゃんと書けたとしても２乗となるとややこしく思う人がいるだろうから、ここはもっと簡単に

y = t × t

と書いてもいいだろう。2.で示した数列も、この数式に則っている。t番目の数字（＝ y ）は t × t だ。

２乗が出てくるので式は「２次式」、曲線は２次曲線と分類される。

直線でざっくり考えるのではなく、曲線として考えることになった。

もし、グラフや軌道に直線の予測しかしなかったらどうなるだろう。大きく外れることもあるだろう。同じ増えるにしても、その勢いがだんだん緩やかになっていることもあるし、加速している場合もあるだろう。そこで直線ではなく、２次関数に寄せることにすると、見事に予測できることがある。すごいぞ、２次関数！

・・・と言いたいところだが、この予測でもまだ足りない場面はある。たとえばスカッシュのボールはあまり弾まないので、壁にあたった後ボールがどれだけ跳ね返るかを読むのはちょっとだけ難しい。そもそもバスケットボールとスカッシュの例をあげたのは、どちらも屋内競技であるからだ。屋外スポーツで風の影響も考える場合、放物線だけ読んでいてもダメだ。

また予測は外れるのである。

次回はさらに複雑な予測を立ててみよう。

　　　　＊　　　　　　　　　　　　＊　　　　　　　　　　　　＊

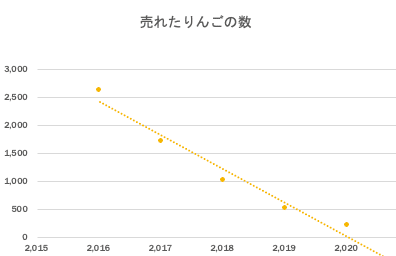
「あれ？タカシくん。２０２１年は、マイナス５００個くらいりんごが売れそうだね」

「そんなバカな！」

（ちなみに見出しのグラフに２次関数を引いてあるが、実際はちょうどゼロになるくらいだと予想できる）

Ver 1.0 2021/6/25