『パターン認識と機械学習（上）』というあの黄色本を用いてゼミを行った際の発表資料をnoteにもアップすることにしました。noteにはゼミ資料を再編集したものをアップします。

本ノートでは、1.2節の発表資料の一部（1.2節のイントロ）をアップし、コメントを記します。資料はできるだけ原著に忠実に作成することを心がけていますが、本noteは、原著だけでなく、自分自身が感じていることも含めてまとめています。

同時確率・周辺確率

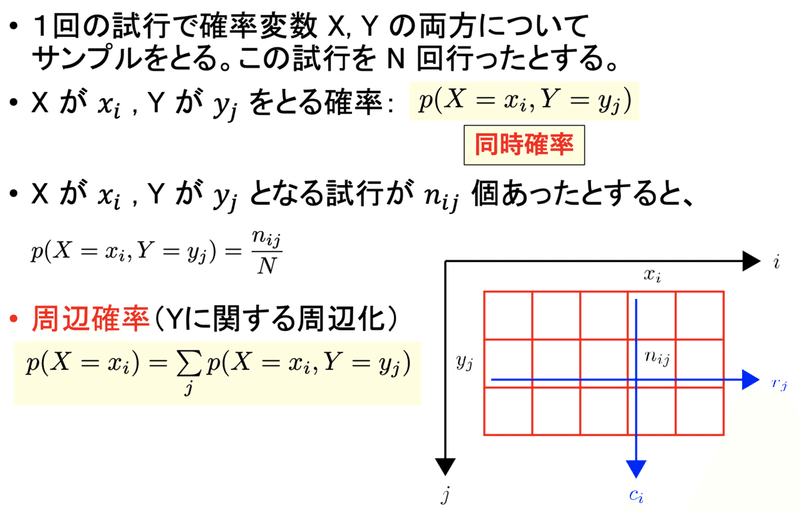
1.2節の最初は同時確率、周辺確率、条件つき確率、ベイズの定理を、箱とフルーツの問題を例に紹介しています。同時確率は「X=aかつY=bとなる確率」のように、２つの条件が同時に成立する確率です。

周辺確率はただ「X=aとなる確率」となる確率のことです。Yの値は関係ありません。数式を使った定義では「X=aかつY=bとなる確率」をbについて足し合わせたものと等しくなります。「同時」「周辺」という言葉や、数式を使った定義のせいで難しく感じてしまいますが、非常にシンプルです。

条件つき確率とベイズの定理

「条件つき確率」と「ベイズの定理」は統計・機械学習・深層学習では必須の知識です。しかし「条件つき」になりすぎると急に難しそうに見えます。

私は「条件つき確率」は全体集合が制限されているだけ、全体集合の見方の問題だと思います。最近の話題では、ワクチンを接種することで重症化率が減少するという話も条件つき確率の話です。「ワクチンを接種していない人のうち」「ワクチンを１回接種した人のうち」「ワクチンを２回接種した人のうち」と言う時は、自然と全体集合の対象を制限しています。

厳密性を欠くかもしれませんが、全体集合を制限することを「条件つき」と考えれば良いと思います。そうすると、大学受験レベルで何通り起こるかを数え上げれることができれば、自然と分子と分母に何が来るかわかり、大学入学共通テストレベルの問題なら困らないはずなのですが…

後半の「ベイズの定理」は「p(X,Y) = p(Y|X)p(X) = p(X|Y)p(Y)」を考えると単純な公式です。1.2節のイントロでは、式が出てきて、後述する箱とフルーツの例の説明があるだけですが、この後の本文では非常に重要な公式となります。

箱とフルーツの問題

1.2節のイントロでは、箱とフルーツの問題を通して、同時確率、周辺確率、条件つき確率、ベイズの定理を説明しています。高校の数学の教科書に載っているレベルの問題を考えています。

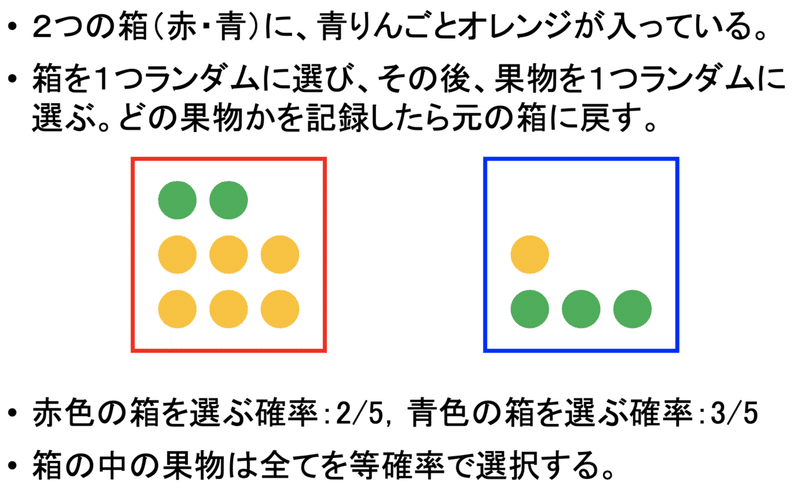
上の条件のもとで、様々な確率を計算すると以下のようになります。箱を選んだ後に、選んだフルーツが「青りんご」「オレンジ」である確率は条件つき確率です。例えば、赤い箱を選ぶと、そこからは全体集合が箱の中の8個のフルーツに制限されます。赤い箱を選んだ後、洗濯したフルーツが「青りんご」である確率は、8個の中から2個を選ぶので1/4となります。全体と部分が何かを意識すれば難しいことはありません。

ベイズの定理・事前確率と事後確率

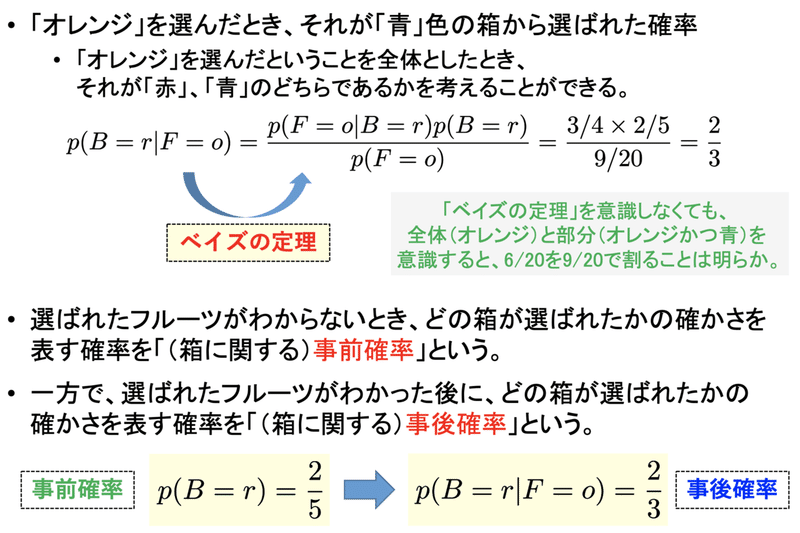
選んだフルーツが「オレンジ」の時、それが赤色の箱から選ばれた確率を考えています。ベイズの定理を使って変形すると、下のようになります。

全体集合がオレンジに制限されていることを考えると、分母に「（箱の色に関係なく）選んだフルーツがオレンジである確率」、分子に「赤色の箱を選んだ後にオレンジ色の箱を選んだ確率」がきて、6/20を9/20で割るという考えは自然なことだと思います。

ここでは「事前確率」と「事後確率」という話も出てきます。自分が持っている情報量で確かさが変わってくるというものです。フルーツがオレンジという情報だけで箱の色に関する確かさが変わることが例として紹介されています。

※『「赤」色の箱から選ばれた確率』が正しいと思います。いつか修正したものと交換します。

条件つき確率と独立

条件つき確率を利用して「独立」が定義できます。他の変数に依存しないということから、条件つき確率が条件つけている変数に依存しないことで、「独立」を定義することができます。

※本資料はGithubにもアップロードしています。本ノートおよびアップロードしている資料について何かありましたら、noteのコメント欄までお願いします。