
AtCoder Beginner Contest反省会 ~2023~
入水したから入青を目指すぞ!
とがんばってたけど、2023年も終わるし、入青はまだまだかかりそうなので一旦区切り。。。
来年の目標。初黄パフォ、入青、初C++での参加、Ratingがサチらないこと。達成できますように。
AtCoder Beginner Contest 307
ARC162で入水し、そこはかとない脱落不安も抱えながら、かつ、朝から高速道路3時間くらい運転して神経すり減らし、疲れて2時間も昼寝して寝ぼけまくった状態で臨んだABC307。ABCDEの5完、パフォーマンス1768、546位という好成績を収めることができた。パフォーマンスは前回がベスト、今回がベスト2、2連続の青パフォ。ということで、Ratingも順調にHighest更新し、1300になった。どうも、いつも易しめの3問目であるCが水Diffだったらしく、面食らった人が多かったようだ。何事もなく解けたので良いパフォーマンスを出せた。Twitterでは水Diffがトレンドになるなど、コンテスト後ちょっと盛り上がっていたが、なんで解けない人が多かったのかわからない。水コーダーなら全員解けるのがぼくの水コーダーのイメージなので意外に感じた。CよりDの方が難しいと思う。Bの意味不明な1ペナがなければ初めて500位以内に入ってベストパフォーマンスが出てたようだ。本当に意味不明で無駄な1ペナだけど、まあそういうこともある。
F - Virus 2
x コンテスト中に40分残っていて、思いついたと思って実装してたが間に合わなかった。その方針はBFSを使っていて、よくなさそうで、結局ダイクストラっぽいのを使った。しかしなかなかうまく整理できず、普通に難しいと思った。ACした後でもスッキリしないなぁという感じで、あまりこの問題について考えたくないほど。考え方としては、1度感染した経路は2度見る必要がなく、次の日はその周囲を調べるということ。しかし、感染者を毎日スタートにして、距離0にしなければならないので、普通のダイクストラのようにはいかない。そこで次の日に感染が進むエッジをプライオリティキューに入れて、感染しうる辺を全部進めてしまう。そこから通常のダイクストラを開始。距離リストのdistを使いまわしていて、気持ち悪いが、前日感染した頂点は見ることがないので、放っておいてよさそうだ。そのあたりの気持ち悪さで、この問題見たくない。辺と頂点、プライオリティキュー2つ使う複雑さ。yellow 2023-06-25
import heapq
INF = 10**16
N, M = map(int, input().split())
ans = [-1]*(N+1)
removed = [False]*M # infected edge
E = []
G = [[] for _ in range(N+1)] # [(to, eid),..]
for _ in range(M):
u, v, w = map(int, input().split())
E.append((u, v, w))
G[u].append((v, len(E)-1))
G[v].append((u, len(E)-1))
K = int(input()) # 要らん
A = list(map(int, input().split())) # 初期感染者
D = int(input())
X = [0] + list(map(int, input().split())) # day is index
dist = [INF]*(N+1)
for a in A:
ans[a] = 0
eq = [] # next edge q [(w, e)]
for a in A:
for nex, e in G[a]:
if ans[nex] == 0:
removed[e] = True
else:
heapq.heappush(eq, (E[e][2], e)) # inf -> non inf
for d in range(1, D+1):
x = X[d]
pq = []
while eq:
w, e = eq[0]
if w > x:
break
if removed[e]:
heapq.heappop(eq)
else: # not removed
u, v, w = E[e]
if ans[v] >= 0 and ans[u] == -1:
heapq.heappush(pq, (w, u))
ans[u] = d
dist[v] = 0
dist[u] = w
elif ans[v] == -1 and ans[u] >= 0:
heapq.heappush(pq, (w, v))
ans[v] = d
dist[u] = 0
dist[v] = w
removed[e] = True
newrem = set()
while pq:
cost, cur = heapq.heappop(pq)
if cost > dist[cur]:
continue
for nex, e in G[cur]:
if not removed[e]:
u, v, w = E[e]
if cost + w <= x:
if cost + w < dist[nex]:
newrem.add(e)
ans[nex] = d
dist[nex] = cost + w
heapq.heappush(pq, (cost + w, nex))
else: # cost + w > x
heapq.heappush(eq, (w, e))
for e in newrem:
removed[e] = True
print(*ans[1:], sep='\n')G - Approximate Equalization
x N = 5000(数列長さ)、|A| = 10^9(値)。O(N^2)。DP。これ自力でいきたいところだが、疲れててなんかわからんとなった。均したら2つの値だけになるということがわかり、low, high=low+1とすると、highはsum(A)/N個であることがわかる。なのでi番目まで確定して、highをj個使っている場合の最小コストでDPすればいい。自然じゃないか?自然に解けないとなぁ。ところで、DPの初期値のINF、最初10^15としたら、WAx2だった。INF=10^16とするとWA解消。どういう場合に10^15でNGになるか考えると、たとえば、前半に10^9が2500個並んでて、後半に-10^9が2500個並んでたら、操作回数は、10^9 + 2x10^9 + 3x10^9 + … + 2500x10^9 + 2499x10^9 + … + 10^9になり、合計を計算すると3x10^15程度になりそう。10^15超えてんじゃん。INFの見積もりでミスってた。INFの見積もりが難しい問題でもあった。 yellow 2023-06-25
INF = 10**16
N = int(input())
A = list(map(int, input().split()))
Asum = [0]*(N+1)
for i in range(N):
Asum[i+1] = Asum[i] + A[i]
sumA = Asum[-1]
low = sumA // N
high = low + 1
amari = sumA % N
dp = [[INF]*(amari+1) for _ in range(N)]
dp[0][0] = abs(A[0] - low)
if amari > 0:
dp[0][1] = abs(A[0] - high)
for i in range(1, N):
fix = A[i] + Asum[i] - low*i
for j in range(amari+1):
temp = fix - j
dp[i][j] = min(dp[i][j], dp[i-1][j] + abs(temp - low))
if j < amari:
dp[i][j+1] = min(dp[i][j+1], dp[i-1][j] + abs(temp - high))
print(dp[N-1][amari])AtCoder Beginner Contest 308
ABD、3完、7ペナ。パフォーマンス707、4093位。なんとここに来てワースト4のパフォーマンスだった。青パフォ2連続からの茶パフォ。ずっこけた。Cが解けなかったのが原因で動揺、Dでも時間を浪費。Eわかったが間に合わず。Fはできる問題だったが見れず。まだまだこういうことが起きる。実際Cなど、勉強になる内容でもあった。
C - Standings
x 計算精度で引っかかってACならず。成功率をA/(A+B)で表す時、成功率の高い順にソートする問題。N = 200000、A, B <= 10^9。A/(A+B)でソートすると、正しくソートできない。おそらくそうだろうと思い、最近覚えたばかりのFractionを使うとTLE!約分しなくてもTLEだったのでなかなか罪が深い。Pythonのsortはkeyのみである。これにA/(A+B)を入れるとWA、Fraction(A, A+B, _normalize=False)を入れるとTLE。Python2のころは比較関数でx<yなら-1、x==yなら0、x>yなら1を返すという使い方だった。keyのみで良いだろうという判断で、Python3では比較関数を渡せなくなったが、今回のケースでは比較関数が有用だろう。sortの引数で、key=functools.cmp_to_key(comp)とすれば良い。これでPyPyで1.5秒で通った。最もスマートな気がする。C++参加者もそうしたはず。
import functools
N = int(input())
AB = [(tuple(map(int, input().split())), i+1) for i in range(N)]
def comp(x, y):
ax, bx = x[0]
ay, by = y[0]
if ax*(ay+by) > ay*(ax+bx):
return -1
elif ax*(ay+by) < ay*(ax+bx):
return 1
elif x[1] < y[1]:
return -1
elif x[1] > y[1]:
return 1
else:
return 0
AB.sort(key=functools.cmp_to_key(comp))
print(*[i for _, i in AB])Decimalを利用する方法もある。Decimalは小数点の誤差がない小数を扱える。ただし罠があって、PyPyはDecimalの処理が遅い。Pythonを選択する必要がある。これでACできた。覚えておきたい。
from decimal import Decimal
N = int(input())
P = []
for i in range(N):
a, b = map(Decimal, input().split())
P.append((-a/(a+b), i+1))
P.sort()
for _, i in P:
print(i, end=' ', flush=True)他の方の提出を見ていて、10^20かけた値を分母は//で割って整数で比較している人がいた。これもトリッキーでおもしろい。//で整数の演算に閉じさせることがキモ。brown 2023-07-01
N = int(input())
AB = [tuple(map(int, input().split())) for _ in range(N)]
P = [(-ab[0]*10**20//(ab[0]+ab[1]), i) for i, ab in enumerate(AB)]
P.sort()
ans = [item[1]+1 for item in P]
print(*ans)D - Snuke Maze
o なぜかバックトラックしてしまい、TLEを発生させて時間を浪費。Cができなくて動揺したか。 2023-07-01
E - MEX
o できる問題だった。もったいない。しかし緑Diffほど簡単?とも思う。数字が0,1,2しかないので、MEXの計算コストが低い。Eでループしながら、累積和で計算しておいたMとXの位置の同じ数字の数を使って計算して解いた。green 2023-07-01
F - Vouchers
o 安い順にソートしておき、商品を順番に追加しながら、使えるクーポンをプライオリティキューに追加していく。一番引けるクーポンを貪欲に使っていけばよい。light blue 2023-07-01
G - Minimum Xor Pair Query
x 上位bitができるだけ一致しているものとのxorをとると一番小さくなる。それはソートしてとなり同士の数字である。という発想。そこまではわかるが、Pythonの標準機能でできない。これもC++が得意なやつ、順序付きのmultisetを使うべき問題。Pythonで自前で順序つきsetを作っている人なんかも見かけるが、Pythonから抜け出せないぼくでも、そこまでする気にはなれない。こういう機会に少しずつC++を使って慣れていきたいところだ。ところで、最初、multiset::findを使っているところで、std::lower_boundを使って実装していたところ、TLE大量発生した。std::lower_boundってmultsetメンバ関数のfindを使うより遅いの?そういうノウハウは、C++をどんどん使っていく中でしか得られない。半年以上やってるPythonですら今回のCのように、知らないこと出てくるのだから。yellow 2023-07-02
// C++
#define rep(i,n) for(int i=0;i<n;i++)
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
multiset<int> X, ans;
int Q;
cin >> Q;
rep(i, Q) {
int q, x;
cin >> q;
if (q == 1) {
cin >> x;
bool a = false, b = false;
multiset<int>::iterator p, n;
multiset<int>::iterator cur = X.insert(x);
n = next(cur);
if (n != X.end()) {
a = true;
ans.insert(x ^ *n);
}
if (cur != X.begin()) {
p = prev(cur);
b = true;
ans.insert(*p ^ x);
}
if (a && b) {
ans.erase(ans.find(*p ^ *n));
}
}
else if (q == 2) {
cin >> x;
bool a = false, b = false;
multiset<int>::iterator p, n;
multiset<int>::iterator cur = X.find(x);
n = next(cur);
if (n != X.end()) {
a = true;
ans.erase(ans.find(x ^ *n));
}
if (cur != X.begin()) {
p = prev(cur);
b = true;
ans.erase(ans.find(*p ^ x));
}
if (a && b) {
ans.insert(*p ^ *n);
}
X.erase(X.find(x));
}
else {
cout << *ans.begin() << endl;
}
}
return 0;
}AtCoder Regular Contest 163
ABの2完、CDを考える時間は十分あったが、無理だった。どちらもおもしろい問題だった。なんとか水パフォは出ていて、Rating+4と横ばいだった。
C - Harmonic Mean
x 1 <= N <= 500。異なるN個の正整数列で逆数の和が1になる組み合わせを作れ。作れなければ'No'。しばらく考えたが閃かず。N=1は1、N=2はNo、N=3は2,3,6が例示されている。式変形で生成する方法が解説されている。1/k = 1/k(k+1) + 1/(k+1)であることを利用すると、1 = 1/2 + 1/2 = 1/2 + 1/2x3 + 1/3 = 1/2 + 1/2x3 + 1/3x4 + 1/4 = 1/2 + 1/2x3 + 1/3x4 + 1/4x5 + 1/5 = …と無限に生成できる。ただし、Nが、6、12、20など、途中で出てくる値だと、異なる正製数列という条件を満たせない。その場合は、N-1個で生成した数列の全要素を2倍し、最初に2を付け加える。すると合計は1になり、Nと被った数字は途中で出てこない。なぜならこの方法で生成する数列は連続する正整数が並んでないから。このあたりはいろいろな方法で解決した人がいたのかもしれないが、この解説のやり方はおもしろいと思う。1/k = 1/k(k+1) + 1/(k+1)という変形は有名で、知っていて使った人が多そうだった。blue 2023-07-02
T = int(input())
for _ in range(T):
N = int(input())
if N == 1:
print('Yes')
print(1)
elif N == 2:
print('No')
else:
ans = set()
for i in range(1, N):
ans.add(i*(i+1))
ans.add(N)
if len(ans) < N:
ans = [2]
for i in range(1, N-1):
ans.append(2*i*(i+1))
ans.append(2*(N-1))
print('Yes')
print(*ans)D - Sum of SCC
x ★数え上げ問題。コンテスト時間中に随分考えたが解決の糸口を見つけられず、完敗した。全頂点間に有効辺を持つグラフをトーナメントグラフというらしい。これを知らなかった。そして、強連結成分分解して縮約するとパスグラフになるという性質を持つ。どの頂点間も辺で繋がっているので、縮約グラフに分岐がありえないことがわかるので、言われてみると確かにそう。問題文にトーナメントと、強連結成分という言葉が両方出てくるので、これをググるのは1つの手だったのかもしれない。が、ぼくはそれをせずに考えていた。そして連結成分Aより上流と連結成分Bより下流の頂点間の辺は、必ずA側からB側に向いているという性質を利用して解く。どう数えるか?化かされたようだが、主客転倒を使う。Aより上流にi個(i = 1 ~ N-1)の頂点があるパターンを数え上げる。すると、1回分割するごとに強連結成分が1つ増えるという考え方で、全グラフパターンに、分割数を全部加えたものが、強連結成分の個数の合計になる。こういう考え方、自然にできるようになりたい。あとはDPでなんとか。最初上流がN個全部の場合をDPの途中で数える必要がないと勘違いして、バグっていた。i = Nも遷移に必要な情報なので、DPの途中では計算し続ける必要がある。orange #DP #トーナメントグラフ #グラフ #主客転倒 #SCC 2023-07-03
mod = 998244353
N, M = map(int, input().split())
COUNT_MAX = N
fact = [0]*(COUNT_MAX+1)
invfact = [0]*(COUNT_MAX+1)
fact[0] = 1
for i in range(1, COUNT_MAX+1):
fact[i] = fact[i-1] * i % mod
invfact[COUNT_MAX] = pow(fact[COUNT_MAX], mod-2, mod)
for i in range(COUNT_MAX-1, 0, -1):
invfact[i] = invfact[i+1] * (i+1) % mod
invfact[0] = 1
def choose(n, r):
return fact[n] * invfact[r] * invfact[n-r] % mod
dp = [[[0]*(M+1) for j in range(N+1)] for i in range(N+1)] # i : vnum, j : Asize, k : small to big count
dp[1][0][0] = dp[1][1][0] = 1
for i in range(1, N): # 配る
for j in range(i+1):
for k in range(M+1):
# add to A
for a in range(j+1):
if k+a > M:
break
dp[i+1][j+1][k+a] = (dp[i+1][j+1][k+a] + choose(j, a) * dp[i][j][k]) % mod
# add to B
for b in range(i-j+1):
if k+j+b > M:
break
dp[i+1][j][k+j+b] = (dp[i+1][j][k+j+b] + choose(i-j, b) * dp[i][j][k]) % mod
ans = 0
for j in range(N):
ans += dp[N][j][M]
print(ans % mod)AtCoder Beginner Contest 309
ABCDE、5完。2140位、緑パフォ1102。Eが難しいと思ったが解かれまくっていた。Eに時間かかってF間に合わず。Fはあと5分あればできてそうだったが、青DIffだった。あれができてればというところだが、Eに時間がかかったのは、難しい解法でやってしまったからだった。そういうミスはある。
E - Family and Insurance
o y代先まで対象、という条件を表現するのに、ぼくはいもす法(的なもの)を使った。ルートから深さ優先探索して、保険開始で+1、y+1代先の深さで-1すれば、いもす的にその人が対象者かわかる。子孫にしか影響してはならないので、帰りがけでセットした情報を削除するような処理をする。なんか面倒で、これができたのが83分。Fが間に合わない原因となってしまった。しかしこの問題、解説ではもっとシンプルに解いていた。深さ優先探索は同じだが、ある人のところから何代先まで保険が効くか?という情報を覚えておき、子供に下るたびに-1する。すると0になったら保険対象ではないことがわかる。なぜこれに気づけなかったかというと、すべての保険の情報を覚えて置かなければならない気がしていて、計算量が大きくなりすぎると勘違いしたから。よく考えたら一番長く続くものだけを覚えておけばよかった。なるほど解かれるわけだ。しかしこれに時間がかかってしまったおかげで青パフォ取れなかったわけで。運命の分かれ道。green 2023-07-08
from collections import deque, defaultdict
from xml.etree.ElementInclude import default_loader
N, M = map(int, input().split())
G = [[] for _ in range(N+1)]
for i, p in enumerate(map(int, input().split())):
c = i + 2
G[p].append(c)
effect = defaultdict(int)
for _ in range(M):
x, y = map(int, input().split())
effect[x] = max(effect[x], y)
level = [-1]*(N+1)
stack = [~1, 1]
level[1] = 0
rem = defaultdict(int)
ans = 0
cureffect = 0
while stack:
cur = stack.pop()
if cur >= 0:
if level[cur] in rem:
cureffect -= rem[level[cur]]
if cur in effect:
cureffect += 1
rem[level[cur]+effect[cur]+1] += 1
if cureffect >= 1:
ans += 1
d = level[cur]
for nex in G[cur]:
if level[nex] == -1:
level[nex] = d + 1
stack.extend([~nex, nex])
else:
cur = ~cur
if level[cur] in rem:
cureffect += rem[level[cur]]
if cur in effect:
cureffect -= 1
rem[level[cur]+effect[cur]+1] -= 1
print(ans)F - Box in Box
o 青Diff。自力でもうちょっとでできたが、コンテスト時間に間に合わず。つらい。Eを順調に解いていれば青パフォいけた。つらい。位置情報付きセグ木を使った。blue 2023-07-08
G - Ban Permutation
x ★ムズい。包除原理であることをまず導けば、なんとなく解けそうなところまでいけるはず。そこからのDPへの持ち込みが難しい。|Pi-i|>=Xであるものをカウントするので、|Pi-i|<Xであるものを引けば良さそう。包除原理でカウントするには、全体から、|Pi-i|<Xを1つ確定した場合のパターン数を引き、|Pi-i|<Xを2つ確定した場合のパターン数を足し、、、とやる必要がある。ここまでは自然。|Pi-i|<Xをj個確定した場合のパターン数をDPで数える。i番目まででj個確定して、i-X~i+Xまでのどれを使っている場合が何通りあるかをDPで数えていく。エグいと思うが、Xが最大5であることからi-X~i+Xのどれが使われているか?は1000程度に収まるとわかる。ウ~ン、難しいなぁ。包除原理とDPを両方ってのも大変だし。勉強になった。こういうの解きたい。2回見てもムズいけど、包除原理の典型として、復讐しよう。全部X以上 -> どれかがX未満であるものをひく -> どれかがX未満である場合の数は、1,2,3,,,NがX未満の数 - 2つ選んでそれがX未満の数 + 3つ選んでそれがX未満の数 - 4つ選んで…と計算できる。iまででj個x未満のものを選択して、iの周辺でどれを使ったか?を状態としてDPする。書いてみてもクレイジーだわ。どれを使ったか?は10幅なので2^10=1000程度、選んだ個数は最大N=100、かけて100000、それが100個。遷移はiを選ばないなら使ったのをスライド、使ったら選択に追加してj+1に遷移か。N個からj個選ぶっていうのはDPの典型的なのだけども。。。これできるか?yellow #包除原理 #DP 2023-07-09
import sys
M = 998244353
N, X = map(int, input().split())
if X > N:
print(0)
sys.exit()
fact = [1]*(N+1)
for i in range(2, N+1):
fact[i] = fact[i-1] * i % M
dp = [[[0]*(2**(2*X-1)) for j in range(N+1)] for i in range(N)] # i:cur, j:fix in advance
dp[0][0][0] = 1
for i in range(X):
dp[0][1][2**(X-1+i)] = 1
for i in range(N-1):
for j in range(N+1):
for k in range(2**(2*X-1)):
nk = k // 2
dp[i+1][j][nk] = (dp[i+1][j][nk] + dp[i][j][k]) % M
if j < N:
temp = i - X + 2
for fix in range(2*X-1):
if 0 <= temp + fix <= N-1:
bit = 2**fix
if 0 == (bit & nk):
dp[i+1][j+1][nk+bit] = (dp[i+1][j+1][nk+bit] + dp[i][j][k]) % M
ans = 0
plumi = 1
for j in range(N+1):
temp = 0
for k in range(2**(2*X-1)):
temp += dp[N-1][j][k]
ans = (ans + plumi * temp * fact[N-j]) % M
plumi *= -1
print(ans)AtCoder Regular Contest 164
AB、2完。C、解きたかった。B、むちゃくちゃ難しいと思うけど、解かれまくってて緑Diffだった。つらいなぁ。Cも緑。Cは閃きの問題で、閃けなかったのは不覚。
B - Switching Travel
x 白黒白黒のように交互に進んで、最後黒の次にすでに通った黒、のように、通った同じ色にぶつかればよいとわかる。ややこしくて、気づくまでずいぶん時間かかった。しかしCに40分残っていて、Cは思い付けば解ける問題だったので、十分時間は残っていたが、C解けず。これ難しいと思うんだけどなぁ。読んだ直後なんて途方に暮れたし。green 2023-07-09
import sys
N, M = map(int, input().split())
G = [[] for _ in range(N+1)]
for _ in range(M):
a, b = map(int, input().split())
G[a-1].append(b-1)
G[b-1].append(a-1)
C = list(map(int, input().split()))
used = [0]*N
count = 0
for s in range(N): # s is start
if used[s] == 0:
count += 1
stack = [s]
used[s] = count
while stack:
cur = stack.pop()
c = C[cur]
for nex in G[cur]:
if used[nex] != count:
if C[nex] != c:
stack.append(nex)
used[nex] = count
else: # used_each[nex]
if C[nex] == c:
print('Yes')
sys.exit()
print('No')C - Reversible Card Game
x 再帰的に計算すれば解けるとは思ったがさすがに計算量が収まらない。解説見ると驚くべき方法だった。Bobは裏表の大きい方をできるだけとればいい。この考え方がコンテスト中に思いついてなかった。不覚。で、実はほぼ大きい方を取れるということがわかる。手元で考えてた時、なんかそんな気がしてたんだけど、詰めきれなかった。大きい方が表のカードが偶数枚のとき、Aliceが1枚裏返すと、奇数枚になる。奇数枚の最小値は1、よってそれをBobは取れば、必ず大きい方を取れる。気づきてぇ~。最初奇数枚だった場合、1枚諦めて偶数枚にすれば、よい。諦めるのは一番AとBの差が小さいもの。なんか詰めきれてない気もしてるけど、とりあえず。発想は押さえたので、オッケーとしよう。これ以上踏み込んでも得るものはない気がする。でもこれは気づきたいなぁ。green 2023-07-09
AtCoder Beginner Contest 310
ABC3完、パフォーマンス928、4134位とボロボロで脱水不可避と思われたが、ギリギリ免れた。どうもインドのKL Universityという大学の学生がおそらく授業かなんかで強制的に参加させられていたらしく、0完が大量発生して相対的にパフォーマンスが上がって助かったようだ。順位表からklu[数字]という名前のユーザーを大量に見つけることができる。3000人くらいいるらしい。不正をしたっぽい人もいて(授業でこれだけ参加させられたらいそうなもの)、運営はその対応に時間がかかったりしていた。ぼくはというと、今週半ばから熱を出して寝込んでいて、ボケボケでなんか頭が働かなかった。入水後ずっと不本意な結果を出し続けて右肩下がりでかなりつらい。入水まで辛かったが、入水後またつらい状況に追い込まれている。ほんと、精神的につらい。あ、あと今回難しかったなぁって思う。結果は病み上がりで頭働かなかったのが原因と思いたいが。
B - Strictly Superior
o 2問目から問題を理解するのがむずかしい。Bにしてはムズいだろう。手こずった。N = 100(商品数)、M = 100(機能数)。全ペアN^2に対して、M個の機能でループして、片方が持っているという状態を調べたので、O(MN^2)で解いたはず。商品ペアで、安いのに同じ機能をすべて持っているものがあったり、同じ値段なのに、機能が包含関係にあったりという、上位互換商品の存在有無を調べる問題。嫌なコードだよねぇ。1ペナしたのは、ケアレスミスで変数初期化位置をミスっていたし、AC時間が33分なので時間ロスし過ぎた。病み上がりには心折れそうだった。投げ出したい気持ちだった。 2023-07-15
import sys
N, M = map(int, input().split())
P = [0]*N
F = [[False]*M for _ in range(N)]
for i in range(N):
p, c, *f_ = map(int, input().split())
P[i] = p
for f in f_:
F[i][f-1] = True
for i in range(N-1):
for j in range(i+1, N):
if P[i] < P[j]:
kaigokan = True
for f in range(M):
if F[j][f] and not F[i][f]:
kaigokan = False
break
if kaigokan:
print('Yes')
sys.exit()
elif P[i] > P[j]:
kaigokan = True
for f in range(M):
if F[i][f] and not F[j][f]:
kaigokan = False
break
if kaigokan:
print('Yes')
sys.exit()
else: # P[i] == P[j]
x = False
y = False
for f in range(M):
if F[i][f] and not F[j][f]:
x = True
if F[j][f] and not F[i][f]:
y = True
if (x and not y) or (y and not x):
print('Yes')
sys.exit()
print('No')C - Reversible
o これも1ペナ。全文字列をsetに入れ、setの要素でループして逆向きのものが入っていたらrem += 1とする。2回カウントしているので、setの要素数からrem // 2を引けば答えになる。というロジックだったが、、、回文が入ってることに気づかず1ペナ。やっぱボケてるよね。回文じゃない場合だけrem += 1するようにした。これ20分かかってんだけど、まだ熱あったんじゃない?って感じ。 2023-07-15
N = int(input())
S = {input() for _ in range(N)}
ans = len(S)
rem = 0
for s in S:
srev = s[::-1]
if s != srev and srev in S:
rem += 1
rem //= 2
print(ans - rem)D - Peaceful Teams
x コンテスト中解けず。50分あったのに。WAが取れなかった。bitDPで解く方針とした。N = 10(人数)、T = 10(チーム数)。とサイズが小さい。最初に作れるグループを全部作っておく。ありうるグループは2^10通りしかないので、少ない。次にbitDPでループする。DPの2つ目のパラメーターはチーム数とする。bitDPで部分集合を列挙できるので、残りの集合でチーム数ごとに遷移すれば良い、と思ったが、部分集合を全部ループさせると、同じグループ分け方法を複数回数えてしまう。つまり、3チームに分ける方法があったときに、その3チームの分け方のどの1チームも部分集合として出てきて、その度にカウントしてしまう。多重カウントを避けるためには、部分集合のうち、特定の一人を含むものだけでループすればよい。その人を含むチームが異なるものを列挙できるので、重なりなく数え上げることができる。というわけで、修正してACできたが、この遷移は結構難しいなと感じた。勉強になった。light blue #数え上げ 2023-07-15
N, T, M = map(int, input().split())
i2bit = [0]*N
for i in range(N):
i2bit[i] = 1<<i # person 0 - (N-1)
ngbit = []
for _ in range(M):
a, b = map(int, input().split())
ngbit.append(i2bit[a-1] + i2bit[b-1])
okg = set()
for g in range(1, 1<<N):
for ng in ngbit:
if (g&ng) == ng:
break # include ng pattern
else: # ok
okg.add(g)
dp = [[0]*(T+1) for _ in range(1<<N)]
for bit in range(1, 1<<N):
if f'{bit:b}'.count('1') == 1:
dp[bit][1] = 1
else: # over 2bit
sub = bit # s is sub
smallest = bit&-bit
while sub:
if sub in okg: # subを1グループに
left = bit - sub
if left == 0:
dp[bit][1] = 1
elif sub & smallest:
for t in range(1, T):
dp[bit][t+1] += dp[left][t]
sub = (sub-1)&bit
print(dp[(1<<N)-1][T])解説を見ると、1人ずつ入れるチームに入れていくだけでできるらしい。たしかにこれで通った。勉強になる。単独の数字をタプルに入れたい時、カンマいるらしい。cur = [((1,),)]とかいたところ。cur = [((1))]とすると、[1]と同じになってしまう件。tupleの処理の練習としてもやってよかった。 2023-07-16
N, T, M = map(int, input().split())
hate = [set() for _ in range(N+1)]
for i in range(M):
a, b = map(int, input().split())
hate[a].add(b)
hate[b].add(a)
cur = [((1,),)]
for i in range(2, N+1):
nex = []
for gs in cur:
t = len(gs)
if t < T:
nex.append((*gs, (i,)))
for g in gs:
for m in g:
if m in hate[i]:
break
else:
ngs = []
for g_ in gs:
if g_ != g:
ngs.append(g_)
else:
ngs.append((*g, i))
nex.append(tuple(ngs))
cur = nex
ans = 0
for x in cur:
if len(x) == T:
ans += 1
print(ans)E - NAND repeatedly
x 本当にダメなんだけども。DP。確かに。サッと解きたいなぁ。light blue 2023-07-15
N = int(input())
S = list(map(int, list(input())))
dp0 = [0]*N
dp1 = [0]*N
ans = 0
if S[0] == 0:
dp0[0] = 1
else:
ans = dp1[0] = 1
for i in range(1, N):
if S[i] == 0:
dp0[i] = 1
dp1[i] = dp0[i-1] + dp1[i-1]
else:
dp0[i] = dp1[i-1]
dp1[i] = dp0[i-1] + 1
ans += dp1[i]
print(ans)F - Make 10 Again
x ダメダメ。やっぱ今回難しいよね。これとか本当にわからなかったし、見たことないパターンだった。DPなんだろうなぁとは思った。10より大きい数字になるものは考えなくても良いので、DPっぽい情報量の圧縮ができると思うので。その先が、最初i番目のサイコロを選ばないことを、0 100%としてやろうとしていた。なんかそれで計算したらうまくいくのでは?と思ってしまい。しかし全体が100%超えてるのでやはり無理だった。どう破綻しているのかも説明できない感じだが、その話は置いておこう。で、ちゃんと100%の状態が、サイコロ1つ振るたびに分岐していって、ちゃんと合計が100%を維持できるような遷移を考える必要がある。その答えは、DPで管理するのは、10以下の選べる数字の集合がSになる確率。うーん、この発想、無い。そのように考えると、次1が出る場合の遷移は、そのサイコロを選ばなければSの要素は選べるのでそのまま追加、そのサイコロだけ選べば1を選べるので追加。それまで選べた数字に1足すことができるので追加。という遷移になる。確率はもちろん1/A。確かにこれで解ける。しかし思いつかないなぁ。どうやったら思いつけるのか。最後に欲しい情報を得られること、全体の確率を1でキープしつつ遷移できること。これを両方満たす方法を考えると思いつくのかなぁ。light blue #確率 #確率DP 2023-07-15
M = 998244353
N = int(input())
A = list(map(int, input().split()))
pow2 = [1]*11
for i in range(1, 11):
pow2[i] = pow2[i-1] * 2
dp = [[0]*(pow2[10]) for _ in range(N+1)]
dp[0][0] = 1
for i in range(1, N+1):
a = A[i-1]
p = pow(a, M-2, M)
for j in range(1, min(11, a+1)):
for s in range(pow2[10]):
if dp[i-1][s] != 0:
ns = s | pow2[j-1] | ((s<<j) % pow2[10])
dp[i][ns] = (dp[i][ns] + dp[i-1][s] * p) % M
if a > 10:
p = p * (a-10) % M
for s in range(pow2[10]):
if dp[i-1][s] != 0:
dp[i][s] = (dp[i][s] + dp[i-1][s] * p) % M
ans = 0
for s in range(pow2[9], pow2[10]):
ans = (ans + dp[N][s]) % M
print(ans)G - Takahashi And Pass-The-Ball Game
x ★激ムズだった。すごい時間かかってAC。問題の構造はわかった。つまり1からKまでの状態でのボール数の合計をKで割るということなので。そしてFunctional Graphなので、1からKでi番目のボールがどのような経路をたどるかは、結構シンプルであることは間違いない。しかしどうやって計算するのかわからんが。K = 10^18だし。解説にFunctional Graphの性質を使う別解も書かれていたが、ここでは触れない。ダブリングの方で解いた。1と2のときの和を考える。1から2進むと3、2から2進むと4なので、1と2の和を2進ませたものは、3と4の和であることがわかる。同じ要領で、1から4までの和を4進ませると5から8までの和になる。Functional Graphの性質使わないとしても頭の中でぐるぐる回っていくのを想像するとおもしろい。しかし、ここまでわかったとして、ダブリングをどう実装するのか?わからなくて理解に時間を要した。解説のこの部分なんだけど。
while(K){
if(K & 1){ // 奇数のとき、はじめとそれ以外に分ける
add(ans, ball);
ball = apply(A, ball);
}
// 2 回の操作をまとめる
add(ball, apply(A, ball));
compose(A, A);
K /= 2;
}K = 10とすると、
1から2を計算し、1と2を足す。
幅が2となり、10は2が5個あると考えられるのでK = 5にする。
5が奇数なので、計算し終わった幅2の部分はansに足しておく。
残りK = 4。
幅2(1,2)から(3,4)を計算し、2つ合わせて幅4を求める。K = 2にする。
同じように幅4を2つ合わせて幅8を求める。K = 1にする。
1は奇数なので、計算した残りの幅8の部分をansに足す。
全部の合計が求まった。
このイメージを自然に得られないが。orange #ダブリング 2023-07-16
M = 998244353
N, K = map(int, input().split())
Kinv = pow(K, M-2, M)
A = []
A.append([0] + list(map(int, input().split()))) # 2^i
B = [0] + list(map(int, input().split()))
step = 2
while step <= K:
nex = [0]*(N+1)
for i in range(1, N+1):
nex[i] = A[-1][A[-1][i]]
A.append(nex)
step *= 2
cur = [0]*(N+1)
for i in range(1, N+1):
cur[A[0][i]] = (cur[A[0][i]] + B[i]) % M
ans = [0]*(N+1)
step = 0
while K > 0:
if K % 2 == 1:
temp = [0]*(N+1) # 意味的にはnex
for i in range(1, N+1):
ans[i] = (ans[i] + cur[i]) % M
temp[A[step][i]] = (temp[A[step][i]] + cur[i]) % M
cur = temp
nex = [0]*(N+1)
for i in range(1, N+1):
nex[A[step][i]] = (nex[A[step][i]] + cur[i]) % M
for i in range(1, N+1):
nex[i] = (nex[i] + cur[i]) % M
cur = nex
step += 1
K //= 2
for i in range(1, N+1):
ans[i] = ans[i] * Kinv % M
print(*ans[1:])AtCoder Beginner Contest 311
ABCDE、5完。Eなかなか閃かず、Fを見て戻ってきて閃いて、87:29にAC。遅かったけど気づけてよかった。Fはお手上げだった。Ratingはちょい上げ。
C - Find it!
o 有向閉路を1つ求める問題。Functional Graphで、自己ループも無いことが保証される条件。よってどこから始めても閉路が見つかることがわかり、シンプルに解いた。自分よりRating上の人でも変な苦労してる人がいたけど、何も苦労せずにいけてよかった。 2023-07-22
D - Grid Ice Floor
o コンテスト中にノーペナで解けたから良かったが、ハマったらヤバいなという嫌な予感を感じる問題だった。すなわち、打ち切り条件ミスったらTLEしそうだなと。壁に当たるまで進むわけだけど、そのあと曲がって進まない条件は?すでに通っていた場合だろう。ということで、すでに通っているか確認したあとで、通ったフラグを立てる。すでに通ってなかった場合は、そのマスをスタックに積む。これでいいはず! 2023-07-22
E - Defect-free Squares
o これコンテスト中に解けたのは、会心の一撃だった気がするけど、結構解かれていた。最大正方形問題、みたいな呼び方をしている人がいたので、典型パターンとしてあるのかもしれないけど、ぼくは知らずに閃いたぞ!(i,j)を右下の端とする最大の正方形をDPする。最大の正方形がわかれば、それより小さい正方形は全部穴なしなので、カウントできることがわかる。DP[i][j]を求めるには、DP[i-1][j]、DP[i][j-1]を見れば良い。同じサイズXだった場合、DP[i-X][j-X]が穴じゃなければDP[i][j] = X+1、穴ならXとわかる。DP[i-1][j]とDP[i][j-1]のサイズが異なる場合は、小さい方のサイズ+1で良いとわかる。気づけたのえらい!二分探索がどうとか言ってた人もいたけど、それよりいい解法のはず。light blue #数え上げ #DP 2023-07-22
H, W, N = map(int, input().split())
hole = [[False]*W for _ in range(H)]
for _ in range(N):
a, b = map(int, input().split())
hole[a-1][b-1] = True
dp = [[0]*W for _ in range(H)] # 最大正方形
for i in range(H):
if not hole[i][0]:
dp[i][0] = 1
for j in range(W):
if not hole[0][j]:
dp[0][j] = 1
for i in range(1, H):
for j in range(1, W):
if not hole[i][j]:
x, y = dp[i][j-1], dp[i-1][j]
if x == y:
if hole[i-x][j-x]:
dp[i][j] = x
else:
dp[i][j] = x+1
else:
m = min(x, y)
dp[i][j] = m+1
ans = 0
for i in range(H):
for j in range(W):
ans += dp[i][j]
print(ans)F - Yet Another Grid Task
x 時間中お手上げで、解説を見たらなるほどと思った。美しいグリッドは黒の下と右下方向に伸ばしたラインの中は全部黒。よく考えたらそうなんだけど、このシンプルな規則に気づかなかった。逆にこれに気づけばなんとかなる問題だった。累積和は極めて自然に思いつく内容。blue 2023-07-22
mod = 998244353
N, M = map(int, input().split())
S = [list(input()) for _ in range(N)]
stopper = [N]*M
for j in range(M)[::-1]:
for i in range(N):
if S[i][j] == '#':
stopper[j] = i
ni, nj = i+1, j+1
while nj < M and stopper[nj] > ni:
stopper[nj] = ni
ni, nj = ni+1, nj+1
break
dp = [[0]*(N+1) for _ in range(M)]
for i in range(stopper[0]+1):
dp[0][i] = 1
for i in range(stopper[0])[::-1]:
dp[0][i] = 1 + dp[0][i+1]
for j in range(1, M):
dp[j][0] = dp[j-1][0]
for i in range(1, stopper[j]+1):
dp[j][i] = dp[j-1][i-1]
for i in range(stopper[j])[::-1]:
dp[j][i] = (dp[j][i] + dp[j][i+1]) % mod
print(dp[M-1][0])G - One More Grid Task
x ★難しい。N = 300、M = 300(グリッドの縦横)、1 <= A <= 300(書かれた数字)。O(NMAmax)長方形内の、最小値x和の最大値を求める。A <= 300から、最小値が300通りしかないということを使えるようだ。たまにこのパターンある。で、最小値mでループして、長方形の下辺はN通りでループする。各列、最小値mを満たすのは上方向にどこまでか?というヒストグラムをO(M)で作ることができる。ヒストグラム内最大長方形はO(M)で作ることができる。和は累積和でO(1)で求まるので、これで解ける。幅固定で各行最小値と和を求めて、Cartesian Treeを使う方法ならA <= 300の条件が不要らしい。これもすごい。思いつかなかった。300は結構小さいと気づく必要がある。300^3=27000000。処理時間2780msでPython提出の中で一番遅いのは気になる。→累積和の上と左に0を入れて条件分岐しなくて良いようにしたら速くなるかと思ったら何も変わらず。なんでやねん!無駄なリスト減らして1922msまで、これでも遅いが。yellow #ヒストグラム内最大長方形 2023-07-23
N, M = map(int, input().split())
A = [list(map(int, input().split())) for _ in range(N)]
Asum = [[0]*M for _ in range(N)]
for i in range(N):
Asum[i][0] = A[i][0]
for j in range(1, M):
Asum[i][j] = Asum[i][j-1] + A[i][j]
if i > 0:
for j in range(M):
Asum[i][j] += Asum[i-1][j]
ans = 0
for m in range(1, 301): # 最小値
histo = [0]*M
for imax in range(N):
for j in range(M):
if A[imax][j] < m:
histo[j] = 0
else:
histo[j] += 1
lr = [[j, j] for j in range(M)]
left = [(-1, -1)] # (hight, id)
for j in range(M):
while left[-1][0] >= histo[j]:
left.pop()
lr[j][0] = left[-1][1]
left.append((histo[j], j))
right = [(-1, M)]
for j in range(M)[::-1]:
while right[-1][0] >= histo[j]:
right.pop()
lr[j][1] = right[-1][1] - 1
right.append((histo[j], j))
for j in range(M):
if histo[j] > 0:
l, r = lr[j]
u = imax - histo[j]
sum = Asum[imax][r]
if l >= 0:
sum -= Asum[imax][l]
if u >= 0:
sum += Asum[u][l]
if u >= 0:
sum -= Asum[u][r]
ans = max(ans, sum*m)
print(ans)AtCoder Beginner Contest 312
Eを約98分で解いて、もうちょっとだったのにとかそういう感情なく、やり切った感で終了。どうやらEが驚くほど解かれていなかったらしく、ぼくがウォッチしているちょっとレベル上の人たちもことごとく解けていなくて驚いた。確認すると400人くらいしか解けてなくて黄Diffだったらしい。逆にFは1000人解いていた。コンテスト中に黄Diff解けたの初めてかもしれない。F以降解いてる人が多いし点数も同じなので残念ながらパフォーマンスは上がらなかったのだが。
C - Invisible Hand
o 2分探索で解いたけど、なんか、Cでこんなに難しいの?ってちょっと思った。一応想定通りだったらしい。茶Diff?うーん。。。brown 2023-07-29
D - Count Bracket Sequences
o DP。(の方が)より多い状態を維持すれば括弧列としては破綻していないので、(が)よりいくつ多いときに何通りあるかでDPする。ちょっと考えて気づけたからよかったけど、結構難しいと思った。括弧列を数えるのは典型で、類題があるっぽい。なんかせこいよなぁ。green 2023-07-29
E - Tangency of Cuboids
o 疑惑のE。これが終わってみると驚くほど解かれていなかった。すごいなぁとウォッチしていた黄コーダーの人も解けてなかったり、ちょっと上のレベルで、目標にしてる人たちもかなり解けてなくて、妙な優越感に浸ることができた。自分だけ解けるってなんか自信つくな。AC400人くらいで、ぼくがコンテスト中に解けた問題の中ではAC数最小かもしれない。黄Diffだし。1辺100の立方体の中だけ見ればいいので、100x100の切断面が3方向合わせてもせいぜい300枚。全てのグリッドに対して接している直方体は多くて2つ。なので、全グリッドに接してる直方体のIDを書き込んでいけばいいなと気づくことができた。原案はAtCoder社長の直大さんらしく、Twitterでも驚くほど解かれていないことに言及されていた。想定解法は、ぼくと違っていて、全1x1x1立方体にそれを含む直方体IDを書き込み、隣り合っている小立方体に異なるIDが書かれていたら接しているとするという方法だった。yellow 2023-07-29
from collections import defaultdict
N = int(input())
objs = [tuple(map(int, input().split())) for _ in range(N)]
xs = defaultdict(list)
ys = defaultdict(list)
zs = defaultdict(list)
for i in range(N):
x1, y1, z1, x2, y2, z2 = objs[i]
xs[x1].append(i)
xs[x2].append(i)
ys[y1].append(i)
ys[y2].append(i)
zs[z1].append(i)
zs[z2].append(i)
xs.pop(0, None)
xs.pop(100, None)
ys.pop(0, None)
ys.pop(100, None)
zs.pop(0, None)
zs.pop(100, None)
ans = [set() for _ in range(N)]
for x in xs:
f = [[set() for _ in range(100)] for _ in range(100)]
for i in xs[x]:
x1, y1, z1, x2, y2, z2 = objs[i]
for y in range(y1, y2):
for z in range(z1, z2):
f[y][z].add(i)
for a in range(100):
for b in range(100):
if len(f[a][b]) == 2:
i, j = f[a][b]
ans[i].add(j)
ans[j].add(i)
for y in ys:
f = [[set() for _ in range(100)] for _ in range(100)]
for i in ys[y]:
x1, y1, z1, x2, y2, z2 = objs[i]
for x in range(x1, x2):
for z in range(z1, z2):
f[x][z].add(i)
for a in range(100):
for b in range(100):
if len(f[a][b]) == 2:
i, j = f[a][b]
ans[i].add(j)
ans[j].add(i)
for z in zs:
f = [[set() for _ in range(100)] for _ in range(100)]
for i in zs[z]:
x1, y1, z1, x2, y2, z2 = objs[i]
for y in range(y1, y2):
for x in range(x1, x2):
f[y][x].add(i)
for a in range(100):
for b in range(100):
if len(f[a][b]) == 2:
i, j = f[a][b]
ans[i].add(j)
ans[j].add(i)
for i in range(N):
print(len(ans[i]))F - Cans and Openers
x Eできたのに、これは解かれまくっていて水Diffなのにできなかった。しかも沼にハマってACまでかなり苦労した。貪欲にやるらしい。つまり、缶切りはたくさん開けれる缶切りから順に使う。缶切りと缶切りが必要な缶はセットなので、缶切りを1つ入手するたびに缶切りが必要な缶を満足度が高い順に開けられるだけ開けながら、S個でどれだけの満足度が得られるか?計算する。缶切り不要の缶も満足度が高い順にT個でどれだけの満足度が得られるか?全部計算してしまう。S+T=Mになる組み合わせを全部計算して、最大の満足度が答え。当然計算量はO(N)だ。しかしなかなかACできなかった。原因は、使わない缶切りと、入手しても開けられない缶切りを考慮し忘れたこと。満足度0でもそれらを計算に含めることによって、合計M個にできる場合があるので、考慮しなければならない。Fが一番しんどかった。最初自分で考えてた時は、K個の和のMAXの問題かと思った。ちなみにぼくはあれがむちゃくちゃ苦手。light blue 2023-07-31
from itertools import accumulate
N, M = map(int, input().split())
easy = []
hard = []
cut = []
for _ in range(N):
T, X = map(int, input().split())
if T == 0:
easy.append(X)
elif T == 1:
hard.append(X)
else: # T == 2
cut.append(X)
easy.sort(reverse=True)
lene = len(easy)
easysum = [0] + list(accumulate(easy))
hard.sort()
lenh = len(hard)
cut.sort()
hardsum = [0]
xsum = 0
while cut:
curc = cut.pop()
hardsum.append(xsum)
while curc > 0 and hard:
curc -= 1
curh = hard.pop()
xsum += curh
hardsum.append(xsum)
while hard:
hard.pop()
hardsum.append(xsum)
ans = 0
for i in range(M+1):
j = M - i
if i < len(hardsum) and j < len(easysum):
ans = max(ans, easysum[j] + hardsum[i])
print(ans)G - Avoid Straight Line
o これは木DPで普通に自力でいけた。F、Gは、訳あって、北千住のコメダで、MacBook Proでやってた。blue 2023-08-01
N = int(input())
G = [[] for _ in range(N)]
for _ in range(N-1):
a, b = map(int, input().split())
G[a-1].append(b-1)
G[b-1].append(a-1)
dp1 = [1]*N
dp2 = [0]*N
dp3 = [0]*N
P = [-2]*N
P[0] = -1
stack = [~0, 0]
while stack:
cur = stack.pop()
if cur >= 0:
for nex in G[cur]:
if P[nex] == -2:
P[nex] = cur
stack.extend([~nex, nex])
else:
cur = ~cur
accum1 = 0
for nex in G[cur]:
if nex == P[cur]:
continue
dp1[cur] += dp1[nex]
dp2[cur] += dp2[nex] + dp1[nex]
dp3[cur] += dp3[nex] + dp2[nex]
dp3[cur] += accum1 * dp1[nex]
accum1 += dp1[nex]
for nex in G[cur]:
if nex == P[cur]:
continue
dp3[cur] += dp2[nex] * (accum1 - dp1[nex])
print(N*(N-1)*(N-2)//6 - dp3[0])AtCoder Beginner Contest 313
ABC、3完でこりゃダメかと思ったが、水パフォが出ていた。D、Eが青Diffで難しかったのと、ノーペナ19:35で3完と速かったので意外と耐えた。
B - Who is Saikyo?
o これ、グラフとか複雑なこと考える必要なくて、最強プログラマーを特定するためには、最強じゃないプログラマーをN-1人特定するだけで良いと気づけたので、早解きできたのが、今回の高パフォにつながった。コンテスト終了後、Twitterでややこしいこと言ってる人結構いた。こういうの気づけるのとても大事だし、良かったと思う。 2023-08-05
D - Odd or Even
x やられてしまった。自分の方針は、たとえばK=3なら、1,2,3、2,3,4、3,4,5、4,5,6、…と順番に質問する。(そういう対象な質問のしかたが自然な気がするので。)すると1,4、2,5、3,6、..の偶奇性がわかるので、1を0確定すれば数珠つなぎで全部確定できて、不整合が起きなければOK、起きたら全部反転すればよいのでは?と思った。しかしNがKで割り切れると、数珠つなぎにならないのでアウトと気付き、そのまま最後まで閃かなかった。解説の方法は賢い。1-Nまでで、上記の質問をするのではなく、1-(K+1)で、上記の質問をすると、K+1回の質問で全数字をK回ずつ含んで質問したことになり、Kが奇数なので、偶奇性は総和と同じ。よって1-(K+1)の偶奇性が総和から確定。あとはK+1回の質問でK個の数字の偶奇性がわかっているから、引けば1-(K+1)までのすべての数字が確定。K+2以降は1つずつ追加して質問すれば毎回確定できる…。天才。だが気づかないといけないと思う。K+1個で最初の質問構成するの…。blue #偶奇性 #XOR 2023-08-06
N, K = map(int, input().split())
ns = list(range(1, K+2)) + list(range(1, K+2))
qs = []
reps = []
xor = 0
for i in range(K+1):
qs.append(ns[i:i+K])
print('?', *qs[-1], flush=True)
rep = int(input()) % 2
reps.append(rep)
xor ^= rep
ans = [0]*(N+1)
for i in range(1, K+1):
ans[i] = xor ^ reps[i]
ans[K+1] = xor ^ reps[0]
fix = reps[0] ^ ans[K]
qfix = list(range(1, K)) # 1~K-1
for i in range(K+2, N+1):
q = qfix + [i]
print('?', *q, flush=True)
rep = int(input()) % 2
ans[i] = fix ^ rep
print('!', *ans[1:], flush=True)E - Duplicate
o D諦めてコンテスト中にこれをやりはじめていたけど、微妙に間に合わなかった。あとでやったら方針は正しく、あと3行くらいでACできるところだった。もったいないが、Dできなかったのだから仕方ない。blue 2023-08-06
import sys
from itertools import groupby
M = 998244353
N = int(input())
S = list(map(int, list(input())))
sg = [(key,len(list(group))) for key,group in groupby(S)]
for i in range(len(sg)-1):
if sg[i][0] != 1 and sg[i+1][0] != 1:
print(-1)
sys.exit()
count = 0
prev = 1
for i in range(len(sg))[::-1]:
if sg[i][0] == 1:
count = (count + sg[i][1] + (prev - 1) * count) % M
else:
count += 1
prev = sg[i][0]
print((count-1)%M)F - Flip Machines
x ★ 激ムズ問題。何が難しいのか?解決すべき問題を正確に小さく分解できれば、その1つ1つは理解できる範囲の問題だと思うが、全体で見るとかなり難しい。最初のうちはスムーズに考察が進むが、途中で徐々に進みが遅くなって思考が停止してしまう。こういうステップが多い問題を解くとき、考えたことを一旦横に置いておいて、別のことを考えて、また戻ってくるというような、脳の一時的な記憶の使い方をするように思う。その要領が無限にあるわけではないので、溢れてしまうと思い出すのに時間がかかって考察が停止してしまうんじゃないか?というような難しさ。書いてるうちに何やってんのかわからなくなってしまった。最初提出した時、REが大量に発生して何かと思ったら、バカでかいリストを作ろうとしていたのが原因だった。P+Q=40で、Pが小さい時、2^Pがかかるアルゴリズムを使い、Qが小さい時、2^Qがかかるアルゴリズムを使うという重い実装が必要だが、if P<Q:で分岐する前のところで、2^Pと2^Q両方使ってしまうミスをしていた。いろんなことを同時にたくさん考えなければならないと、気配りができなくなって細かいミスが増えるのだろうと思う。こういう問題は変数名もわけがわからなくなるので、センスが問われる。これも一応期待値の問題だったが、期待値の部分は難しくなかった。red #期待値 #DP #全探索 2023-08-18
G - Redistribution of Piles
x ★ 方針までは自力で思いつけるが、そこから「Floor Sum」という新しいアルゴリズムを使って高速に処理する必要があり、勉強して実装したのでACに時間がかかった。参考リンクで勉強して実装した。一応式変形を理解したが、0から自力で式変形して再構築するのは大変そうではある。どうしてもやらなければならない状況ならやるだろうけど。式変形のポイントは、割る数のMの倍数を分子に足したらFloorのそとにくくり出せるということとか、Floorの値と正数を比較する不等式でFloor自体を消せるとか。頭の片隅に入れておくと将来役立つこともあるかも。orange #FloorSum #式変形 2023-08-13
from itertools import groupby
def floor_sum(n, m, a, b):
ret = 0
while n > 0 and m > 0:
ret += (a // m) * n * (n-1) // 2 + (b // m) * n
a, b = a % m, b % m
last = a * n + b
n, m, a, b = last // m, a, m, last % m
return ret
M = 998244353
N = int(input())
A = list(map(int, input().split()))
A.sort()
AG = [(k, len(list(g))) for k, g in groupby(A)]
Asum = [()]*(len(AG))
Asum[-1] = AG[-1]
for i in range(len(AG)-1)[::-1]:
Asum[i] = (AG[i][0], Asum[i+1][1] + AG[i][1])
num = N*Asum[0][0]
ans = Asum[0][0] + 1
# print('ans init', ans)
for i in range(1, len(Asum)):
n = Asum[i][0] - Asum[i-1][0]
ans += floor_sum(n, N, Asum[i][1], N + num + Asum[i][1])
num += n*Asum[i][1]
print(ans % M)AtCoder Beginner Contest 314
5完で864位、過去ベスト3のパフォーマンス1595が出てHighest更新、Rating 1306となった。期待値苦手意識あって、Eでうわ~ってなって、しばらく途方にくれてからFに行って、Fも期待値かぁとうろうろして、腹くくってEに取り組んだら思いついて解けた。Fもグラフ確定だから難しくないのでは?と気づいていたが、実際簡単な問題だった。これを機に期待値の問題の苦手意識克服できたらと思う。
E - Roulettes
o なんか思いつけた。うれしい。後ろから期待値のDPする。 いくらのコストをかけると、どの割合で、残りコストの期待値がどれだけになるか?遷移を記述できるので、Mから遡って確定できる。blue #期待値 #DP 2023-08-12
from collections import defaultdict
N, M = map(int, input().split())
CS = []
PS = []
for _ in range(N):
c, p, *s = map(int, input().split())
d = defaultdict(float)
for n in s:
d[n] += 1
for i in d:
d[i] /= p
if len(d) == 1 and 0 in d:
continue
CS.append(c)
PS.append(d)
dp = [10**20]*(M+1)
for m in range(M)[::-1]:
for i in range(N):
c = CS[i]
d = PS[i]
k = 1
right = c
for x in d:
if m + x >= M:
continue
if x == 0:
k -= d[x]
else:
right += d[x]*dp[m+x]
dp[m] = min(dp[m], right / k)
print(dp[0])F - A Certain Game
o コンテスト終了後解けた。苦手意識から難しいと思っていたが、グラフ確定して上から辿っていくだけなので、難しい問題ではないと思う。blue #期待値 2023-08-12
M = 998244353
class Union():
def __init__(self, n):
self.par = [i for i in range(n)]
self.rank = [0 for _ in range(n)]
def find_root(self, v):
if v == self.par[v]:
return v
else:
# can go to the root directly
self.par[v] = self.find_root(self.par[v])
return self.par[v]
def same_tree(self, x, y):
return self.find_root(x) == self.find_root(y)
def unite(self, x, y):
x = self.find_root(x)
y = self.find_root(y)
if self.rank[x] < self.rank[y]:
self.par[x] = y
else:
self.par[y] = x
if self.rank[x] == self.rank[y]:
self.rank[x] += 1
N = int(input())
G = [[0] for _ in range(2*N)] # p and children
uf = Union(N+1)
count_and_node = [(1, i) for i in range(N+1)]
node = list(range(N+1))
cur = N+1
for _ in range(N-1):
p, q = map(int, input().split())
proot = uf.find_root(p)
qroot = uf.find_root(q)
pc, pn = count_and_node[node[proot]]
qc, qn = count_and_node[node[qroot]]
total = pc+qc
inv = pow(total, M-2, M)
uf.unite(proot, qroot)
count_and_node.append((pc+qc, cur))
G[pn][0] = pc*inv%M
G[qn][0] = qc*inv%M
G[cur].extend([pn, qn])
root = uf.find_root(proot)
node[root] = cur
cur += 1
for n in range(N+1, 2*N-1)[::-1]:
p, c1, c2 = G[n]
G[c1][0] = (G[c1][0] + p) % M
G[c2][0] = (G[c2][0] + p) % M
print(*[G[n][0] for n in range(1, N+1)])G - Amulets
x 苦手な上と下に分けるやつだったのか。そこに持っていくことすらできなかった。i番目のモンスターまで倒すときに必要なお札(amulet)の数を求めると、お札の数ごとに倒せるモンスター数が確定できるのでそのようにする。i番目のモンスターまでに各タイプのモンスターごとに攻撃で受けるダメージの合計が確定することがわかる。お札は貪欲にダメージが大きい順に使うのが最適。ダメージが大きい順にお札を使っていって、何枚使うと、総ダメージがH-1以下に抑えられるか?調べればよい。すると上と下に分けて処理するやつにたどりつく。苦手だけどそろそろ克服しないといけない。状態遷移を正確に整理すること。上だったのを下に移動するのか?上のものを上のままにするのか?という条件ごとに処理が確定する。元々上にいたか?下にいたか?という情報は必要なので、フラグで管理する。など。ある程度はテンプレ的に決めていける。yellow #上と下に分けるやつ 2023-08-16
import heapq
N, M, H = map(int, input().split())
D = [0]*(M+1) # current total damage
ans_ = [0]*(N+1)
amulet = 0 # need how many ? 0 at first
pql = [(0, i) for i in range(1, M+1)] # (-d, mid)
which = [0]*(M+1) # 0 is smaller 1 is amulet
heapq.heapify(pql)
curD = 0
pqr = [] # (d, mid)
for i in range(1, N+1):
A, B = map(int, input().split())
pd = D[B]
D[B] += A
while pql and -pql[0][0] < D[pql[0][1]]:
heapq.heappop(pql)
if pql and D[B] <= -pql[0][0]:
heapq.heappush(pql, (-D[B], B))
which[B] = 0
curD += A
while curD > H - 1:
while -pql[0][0] < D[pql[0][1]]:
heapq.heappop(pql)
d, mid = heapq.heappop(pql)
heapq.heappush(pqr, (-d, mid))
curD += d
which[mid] = 1
amulet += 1
else:
heapq.heappush(pqr, (D[B], B))
if which[B] == 0:
curD -= pd
which[B] = 1
amulet += 1
while True:
while pqr and pqr[0][0] < D[pqr[0][1]]:
heapq.heappop(pqr)
if pqr and curD + pqr[0][0] <= H - 1:
d, mid = heapq.heappop(pqr)
heapq.heappush(pql, (-d, mid))
curD += d
which[mid] = 0
amulet -= 1
else:
break
ans_[i] = amulet
ans = [0]*(M+1)
pm = ans_[N]
for j in range(pm, M+1):
ans[j] = N
for i in range(1, N)[::-1]:
if ans_[i] != pm:
for j in range(ans_[i], pm):
ans[j] = i
pm = ans_[i]
print(*ans)AtCoder Grand Contest 064
入水済みなので、はじめてのAGC Rated参加となった。A、1完。B、よいところまでひらめいていて、残り5分くらいでWAx2だった。ジャッジが終盤までACで推移してたので、興奮して見守りながら、WAに変化していく絶望ったらない。そのままコンテスト終了。949位、パフォーマンス1022で新Rating 1281に冷えてしまった。Aに時間がかかってパフォーマンス落ちたが、Bが解けていればというところ。
A - i i's
o 時間がかかってしまい、1完だったのでパフォーマンス落とした。正解の数列を生成するロジックをプログラムで組もうとしていたのが間違い。決め打ちでこの順序ならOKという並びを作れる。気づいたのが72分くらいだったので、遅かった。慣れるとそういう方針もあると、もっと早く気づけるかもしれない。みんなそれなりに時間かかってたので結構難しい気はする。green 2023-08-13
N = int(input())
X = list(range(1, N-1))
Y = []
for _ in range(N-1):
X.extend([N, N-1])
X.append(N)
for n in range(N-2, 0, -2):
for _ in range(n-2):
X.extend([n, n-1])
if n > 1:
X.append(n)
print(*X)B - Red and Blue Spanning Tree
x 時間中WAx2で力尽きた。しかし3時間のコンテストで最後までかなり集中できたし、キーとなる考察である、エッジの色と両端点の色のパターンでエッジを分類するというところまでひらめくことができた。で、ぼくはまず、エッジと両端が同じ色のものは最初に全部UnionFindでつないだ。ここまでは良い。その後、まだ条件を満たすエッジとつながっていない頂点を条件を満たすエッジでどんどん接続していった。最後に全エッジでもう一度UnionFindして、全頂点条件満たすように完成したらOKというロジックで出した。ところ、06_cycle_05と06_cycle_06だけがWA。実はロジックに穴があるのに、ACx75、WAx2までいくとは。期待させて突き落とされた感じ。実は、最初に同色でつないで条件を満たしたものから、まだつながってない頂点に、条件を満たすエッジを伸ばしていく形で、余った頂点を全部接続できなければいけないらしい。ぼくの最初のやり方では抜けがあるのだろう。悔しいが、また次がんばるしかない。方針変更後、TLEの解消にもちょっと時間がかかった。結局完敗だった。blue #グラフ 2023-08-13
AtCoder Beginner Contest 315
ABCDE、5完、845位、過去ベスト4の1577というパフォーマンス。なかなかよかった。どうもウォッチしてる人を見ると、Dが解けてない人が結構いるようだった。解かれてないこともないけど、レベル高い人の中にも解けなかった人を散見した。ぼくもちょっと詰まったが、閃いて解くことができた。E完了時点で残り35分。Fはしばらく考えて不可能だろうと思って諦めてGへ。拡張ユークリッド互除法を使うことまでひらめいて興奮したけど、過去に問題に適用したことがなく、瞬発力を出せなくてコンテスト時間内に間に合わなかった。その後、Fが1からNまで順番に通る問題だったことに気づき、ショックを受けた。順序も選べると勘違いしていた。そりゃ解けないよ。しかも順番が決まっているのなら簡単な問題の上、解いてれば3度目の青パフォでベストパフォーマンスを出せていた。Gまで解ければ150位くらいの黄パフォでフィーバー。F、Gはコンテスト終了後どちらも自力ACしたので、自分が黄パフォを出せるところに近づいてることを実感しつつも、悔しさや歯がゆさが強く残るコンテストとなった。
D - Magical Cookies
o たしかになかなか難しいと感じたが、ひらめいて35分くらいでAC。できてない人を散見した。たまにウォッチしてる人たちがミスってるのを自分は解けるということがでてきて、うれしい。ABC312 Eとか。モチベーションがあがる。ってあれ?このコードいいのかなってところが^^; 全行全列を色と数 のdictにつっこむ。1色で2つ以上の場合はそれを別方向のdictから引く。止まるまで繰り返す。light blue 2023-08-19
from collections import defaultdict
H, W = map(int, input().split())
C = [list(input()) for _ in range(H)]
hd = {i:defaultdict(int) for i in range(H)}
wd = {i:defaultdict(int) for i in range(W)}
for i in range(H):
for j in range(W):
hd[i][C[i][j]] += 1
wd[j][C[i][j]] += 1
while True:
rem_c_from_w = defaultdict(int)
rem_h = []
for i in hd:
if len(hd[i]) == 1:
c, left = hd[i].popitem()
if left > 1:
rem_c_from_w[c] += 1
rem_h.append(i)
rem_c_from_h = defaultdict(int)
rem_w = []
for j in wd:
if len(wd[j]) == 1:
c, left = wd[j].popitem()
if left > 1:
rem_c_from_h[c] += 1
rem_w.append(j)
if len(rem_h) == len(rem_w) == 0:
break
for i in rem_h:
hd.pop(i)
for j in rem_w:
wd.pop(j)
for j in wd:
for c, n in rem_c_from_w.items():
wd[j][c] -= n
if wd[j][c] == 0:
wd[j].pop(c)
for i in hd:
for c, n in rem_c_from_h.items():
hd[i][c] -= n
if hd[i][c] == 0:
hd[i].pop(c)
print(len(hd)*len(wd))F - Shortcuts
o チェックポイントを任意の順序で通るのだと勘違いしていたが、終了後解けた。難しくない。勘違いがなければコンテスト中にACして過去1のパフォーマンスを出せただろうという問題。くやしい!!!取り返しがつかない。blue #DP 2023-08-19
INF = 10**15
N = int(input())
pena = [0, 1]
for i in range(2, 30):
pena.append(2 * pena[-1])
XY = [tuple(map(int, input().split())) for _ in range(N)]
dp = [[INF]*30 for _ in range(N)]
dp[0][0] = 0
for i in range(N-1):
for j in range(30):
if dp[i][j] == INF:
continue
for jpla in range(29-j):
ni = i + jpla + 1
if ni < N:
x, y = XY[i]
x_, y_ = XY[ni]
dist = ((x-x_)**2 + (y-y_)**2)**0.5
nj = j + jpla
add_pena = pena[nj] - pena[j]
dp[ni][j+jpla] = min(dp[ni][j+jpla], dp[i][j] + add_pena + dist)
print(min(dp[N-1]))G - Ai + Bj + Ck = X (1 <= i, j, k <= N)
o Fをスキップしてコンテストの最後にこれを見ていたが、拡張ユークリッド互除法を使うまで見えていたが、間に合わず。終了後自力ACできた。このアルゴリズムは、コンテストで学んだのではなく、自主的な勉強で学んでいた。しかもすげーと感動して印象に残っていたのに、1次不定方程式の全解生成の部分が定着できておらず、とっさにコンテスト中の短時間で対応できなかった。非常にくやしいが、これが解ける可能性を感じることができた。ここまでコンテスト中に解くと150位黄パフォで、フィーバーだった。yellow #拡張ユークリッド互除法 2023-08-19
def extgcd(a, b):
if b:
d, y, x = extgcd(b, a % b)
y -= (a // b) * x
return d, x, y
return a, 1, 0
N, A, B, C, X = map(int, input().split())
d, x, y = extgcd(B, C)
B_, C_ = B // d, C // d
ans = 0
for i in range(1, N+1):
Y = X - A * i
if Y < B + C:
break
if Y % d != 0:
continue
m = Y // d
tmin = (1-m*x) // C_
if (1-m*x) % C_ != 0:
tmin += 1
tmax = (N-m*x) // C_
tmin2 = (m*y-N) // B_
if (m*y-N) % B_ != 0:
tmin2 += 1
tmax2 = (m*y-1) // B_
tmin = max(tmin, tmin2)
tmax = min(tmax, tmax2)
if tmin <= tmax:
ans += tmax - tmin + 1
print(ans)AtCoder Beginner Contest 317
遅めの4完。パフォーマンス1039、順位2571。Dが簡単とは思えなかったので、他の人のレベルの高さを感じた。
D - President
o 各選挙区で追加で必要な人数と、そのときに得られる議席数を計算できる。つまり、コストと、ゲインのリストが与えられて、ゲインの合計を一定以上にするための最小コストを調べる問題ということになる。結局DPで解いたけど、DPであることに気づくのに結構時間がかかったのが敗因。悩んだときに、DPでできない?って1度は疑っても良いかも。みんなたやすくできてるのは、典型だからかと思う。green #DP 2023-08-26
E - Avoid Eye Contact
o よくあるグリッド上の最短経路を求める問題で、緑Diffにもかかわらず、コンテスト中にACできなかった。最初ダイクストラで最短経路を出していて、TLEとMLEが出て、ダメダメだった。そういえばダイクストラとBFSってどう使い分けてたっけ?と今さらながら気になった。BFSはすべての辺の距離が同じときしか使えないということだった。なのでグリッドは使える。BFSでやるとACできたが、遅い。グリッドの通れる位置をグラフ化すること自体も無駄な処理なのかと。絶対に通らないところもグラフ作るためだけに処理しちゃうし。学びの多い問題。#最短経路 #BFS 2023-08-26
F - Nim
x あたおか。桁DPと気づけないなぁ。Xi <= Nという条件から、k桁目まででN以下かというフラグをDPのパラメーターに入れる、というのは、そうだよねと思いつけたほうが良い。あとは特定の数で割ったあまり。これも桁DPでよく出てくる。k-1桁までであまりがaである場合の数をDPで処理していく。言われてみると結構見たことあるような手法に思えてくる。あとはDPで遷移できることを確認しないといけないが、k+1桁目がNより小さい、大きい値であれば、k+1桁目まで全部で当然小さい、大きい値になる。k+1桁目がNと一致する場合は、k桁目までがN以下ならN以下、Nより大きければNより大きい、ということでNより大きいかフラグはk+1桁目を決めれば遷移できることがわかる。1<=X<=Nという条件だったので、どれかのXが0の場合を引く必要があるが、これは確かに最小公倍数の倍数の個数なので、別途計算可能。難しい。とはいえ、Dと同じで、この問題なんかも、見た瞬間に桁DPじゃない?って思ってもおかしくはない。yellow #桁DP 2023-08-26
import math
M = 998244353
N, *A = map(int, input().split())
bigger = []
for bit in range(8):
bigger.append((False if (bit&1)==0 else True,
False if (bit&2)==0 else True,
False if (bit&4)==0 else True))
ptns = [(0,0,0), (0,1,1), (1,0,1), (1,1,0)]
i2big = [1,2,4]
dp = [[[[0]*A[2] for _ in range(A[1])] for _ in range(A[0])] for _ in range(8)]
dp[0][0][0][0] = 1
# for k in range(5):
for k in range(61):
kbit = 1<<k
amari = [kbit%A[0], kbit%A[1], kbit%A[2]]
Nk = 0 if (N&kbit) == 0 else 1
ndp = [[[[0]*A[2] for _ in range(A[1])] for _ in range(A[0])] for _ in range(8)]
for big in range(8):
for a0 in range(A[0]):
for a1 in range(A[1]):
for a2 in range(A[2]):
if dp[big][a0][a1][a2] == 0:
continue
for ptn in ptns:
big_n = 0
for i in range(3):
if ptn[i] > Nk or (ptn[i] == Nk and bigger[big][i]):
big_n += i2big[i]
na0 = (a0 + amari[0] * ptn[0]) % A[0]
na1 = (a1 + amari[1] * ptn[1]) % A[1]
na2 = (a2 + amari[2] * ptn[2]) % A[2]
ndp[big_n][na0][na1][na2] = \
(ndp[big_n][na0][na1][na2] + dp[big][a0][a1][a2]) % M
dp = ndp
rem = 1
rem += N // (A[1] * (A[0] // math.gcd(A[0], A[1])))
rem += N // (A[2] * (A[1] // math.gcd(A[1], A[2])))
rem += N // (A[0] * (A[2] // math.gcd(A[2], A[0])))
print((dp[0][0][0][0]-rem) % M)G - Rearranging
x ★ 激ムズで自力で閃けるような気はしない。ホールの定理により、この答えは必ずYesとなるとのこと。ぼくも考えるときに、Noのパターンを作れるか?と考えてたけど作れなくて、これはNoを作るの不可能なのでは?と思っていたけど、実際にNoはないらしい。というわけで、ホールの定理を勉強しなければならない。大変だ。2部グラフ辺彩色というアルゴリズムも知られており、こちらが高速らしい。これも勉強しなければならない。大変だ。まあこの問題にはホールの定理だけで十分だからいいや。というわけで、解説を読めばアイデアだけは、理解できるので、ACできたが、その背後にあるロジックの勉強でしばらく時間がかかりそう。とはいえ、このアイデアは頭に刻み込んでおかないとなぁ。整列後の1列に注目すると、1-N行目と1-Nという数字が1対1にマッチングしていることがわかる。そこから1-Nと1-Nの完全マッチングを連想できるか?って話。orange #ホールの定理 #最大流 #2部グラフ辺彩色 2023-08-27
ホールの定理の証明を理解した。2部グラフをAとBのグループとする。Aの部分集合aに対して隣接するBの部分集合bの要素数が、常に|a|以上の場合、Aはすべてマッチできるという定理。この問題における、ホールの定理の条件は?というと、例えばi行とj行に必ず2つ以上の値がなければならないということになるが、それは必ずある。なぜなら同じ値はM個しかないから。2行が全部同じ値だと2M個同じ値ということになってしまう。よってホールの定理が成り立つ。そして1-Nをある列に移動して使ったとする。残りは全部M-1個になる。それでもやはりホールの定理の条件を満たしている。よって、1-Nをどんどん左の列から順番に確定していけば正解の並びを作れることがわかる。そこまでちゃんと考えるのムズいじゃん。そのホールの定理は、帰納法で証明する。Aの要素が1つの場合は自明だろう。2以上の場合、Aの真部分集合aに対して、隣接する集合bは常に|a| < |b|だった場合、適当にu-vをマッチングさせると、残ったAのすべての真部分集合に対して|a| <= |b|が成り立つ。uだけか、uとvを含んでいれば|a| < |b|のままだし、vだけ含まれていて、b側だけ減っても少なくとも|a| <= |b|が成り立ち、帰納法の仮定から、常に成り立つ。真部分集合aで、|a| == |b|のものがある場合はどうか?帰納法の仮定で、aとbは完全マッチングできる。aと排他的な部分集合a'を考える。a+a'に隣接するb+b'が考えられるが、|a+a'| <= |b+b'|であり、今考えているのは|a| == |b|の場合だったので、a'とbは一切隣接していない。よって、a'はすべてb'と隣接している。よって|a'| <= |b'|が成り立つ。帰納法の仮定からa'はすべてマッチングできる。よってこの場合もAはすべてマッチングできることが示された。 2023-08-28
N, M = map(int, input().split())
mf = MF(2*N+2)
S, T = 0, 2*N+1
for v in range(1, N+1):
mf.add_edge(S, v, 1)
mf.add_edge(v+N, T, 1)
for a in map(int, input().split()):
mf.add_edge(v, a+N, 1)
ans = [[] for _ in range(N)]
used = [set() for _ in range(N)]
for _ in range(M):
mf.mf(S, T)
for i in range(N):
v = i + 1
for j, e in enumerate(mf.g[v]):
if j in used[i]:
continue
to, capa, rev = e
if capa == 0:
rev[1] = 0
ans[i].append(to-N)
used[i].add(j)
break
mf.g[S][i][1] = 1
mf.g[S][i][2][1] = 0
mf.g[T][i][1] = 0
mf.g[T][i][2][1] = 1
print('Yes')
for x in ans:
print(*x)AtCoder Beginner Contest 318
5完、同じくらいの人たちみんな5完だけど遅いのでパフォーマンス低い。なんとかしたい。Fを解かないと差をつけられない。しかしこのFは難しかった。いや、ひらめけないとも思わないが。Gも最大流であることは自力で気づいた。頂点を辺に変換するところまでは気づけなかったが、極めて自然な発想なので、全く難しいとは思わない。これはいけるなぁとも思う。
D - General Weighted Max Matching
o できたが時間かかってしまった。前回DPでできないか早いうちに疑え!という教訓を得たにも関わらず、またDPでいけると気づくのに時間がかかってしまった。40分も使っており、痛すぎる。多分同レベルの人たちは、あ、DPだぁとすぐ思って短時間で解いてる。そこで時間に差がつく。痛い。green #bitDP 2023-09-02
F - Octopus
x ★ 勉強になった。いい問題だなぁと思う。同じような雰囲気の問題を苦労して考察してるときに、こういう考え方をしたことは、おそらくあったと思う。しかし必要なときにさっと出てくるようなものではない。類題を解いた経験は今後きっと役に立つ。座標の範囲が10^18と広い。しかしk->k+1とタコの頭を移動したときに掴めてたのが掴めなくなったり、掴めなかったのが掴めるようになったりするのはどういうときか?考える。k+LがXに乗った時、k-LがXから外れた時、この2つの場合しかありえないことがわかる。そのとき、k=X-L-1またはk=X+Lである。XとLはN=200しかない。ということは、状態が変化しうるkは、XとLの組み合わせ数、すなわちN^2=40000しかないということだ。k->k+1で変化するkなのだから、40000通りのkについてだけ、全部掴めるかどうか?調べれば良い。kで掴めれば、1つ小さいkとの間は総取り、掴めなければそこは無理だ。両端は調べなくて良い。無限遠と状態が同じであることから、絶対に無理であることが確定しているので。おもしろい問題だぁ。このアイデアは身につける!yellow 2023-09-02
N = int(input())
X = list(map(int, input().split()))
L = list(map(int, input().split()))
L.sort(reverse=True)
meank = set()
for x in X:
for l in L:
meank.add(x-l-1)
meank.add(x+l)
meank = sorted(meank)
nk = len(meank)
ans = 0
for i in range(1, nk):
k = meank[i]
dist = [abs(x-k) for x in X]
dist.sort(reverse=True)
for d, l in zip(dist, L):
if d > l:
break
else:
ans += k - meank[i-1]
print(ans)G - Typical Path Problem
x ★ B->A,Cの最大流であることは自力で気づいた。頂点を辺に変換するところまでは気づけなかったが、極めて自然な発想なので、全く難しいとは思わない。これはいけるなぁとも思う。典型問題と言える。ずばり、頂点を辺にする。辺にしてキャパを1とすれば、その頂点を1度しか通らないことを表現できる。自然だと主う。恐怖心さえなくして考えれば、知らなくても自力AC可能だったかもしれない。で、実際の辺をつなぐときは、頂点の出口と頂点の入り口をつなぐようにすればいい。yellow #最大流 2023-09-02
N, M = map(int, input().split())
A, B, C = map(int, input().split())
S, T = 0, 2*N + 1
mf = MF(2*N+2)
for _ in range(M):
u, v = map(int, input().split())
mf.add_edge(u, v+N, 1)
mf.add_edge(v, u+N, 1)
for u in range(1, N+1):
mf.add_edge(u+N, u, 1)
mf.add_edge(S, B, 2)
mf.add_edge(A, T, 1)
mf.add_edge(C, T, 1)
if mf.mf(S, T) == 2:
print('Yes')
else:
print('No')AtCoder Beginner Contest 319
ABCDE、5完。1095位、パフォーマンス1517。まあまあの成績。これでは伸びないけど。5完でも20分で解いた人は260位とか、すごい良い順位。ぼくは95分。遅いのが結構効いている。でもなかなか速くならないんだよなぁ。今回から7問制になるらしい。一時的なもの?って思ったけどずっとらしい。
B - Measure
問題の読解が苦しかった。何も考えず、機械的にコード書いたら解けるんだけど、なんか意味を捉えようとすると読解に時間がかかってしまう。Bまでで11分半なので、そりゃだめだよなぁ。社長原案らしい。考えるのやめようw 2023-09-09
Bの原案でした。N等分が書いてある定規で数を書くべき場所を出題したかったんだけど、多分記述の厳密性の都合でただの式になった気がするw
— chokudai(高橋 直大)@AtCoder社長 (@chokudai) September 9, 2023
C - False Hope
o これ解いた時点で40分。実装で苦労してしまったパターン。kyopro_friendsさんの提出を参考にやり直してみよう。こういうのが反省対象だろう。あ、permutationsの使い方が違う。a == p[i]と考えるのではなく、i == p[a]と考えるのか。そういう解釈も確かにできる。挿入DPを理解するのに苦労したみたいな、見方の変更だなぁ。それに加え、x,y,zを循環させる処理。これもぼくは3通りを個別に全部書いてたので。green 2023-09-09
from itertools import permutations
C = []
for i in range(3):
C.extend(list(map(int, input().split())))
NG = 0
ALL = 362880
for perm in permutations(range(9)):
ng = False
for x, y, z in [(0,1,2), (3,4,5), (6,7,8), (0,3,6), (1,4,7), (2,5,8), (0,4,8), (2,4,6)]:
for _ in range(3):
if C[x] == C[y] and perm[x] < perm[z] and perm[y] < perm[z]:
NG += 1
ng = True
break
x, y, z = y, z, x
if ng:
break
print(1-NG/ALL)F - Fighter Takahashi
x ★ 激ムズ問題。これは計算量の見積もりも大事なやつ。しかし実装重すぎて方針気づいても時間内にできる気がしないな。ちゃんと、順序立てて考察しよう。まず敵は倒せるだけ倒せば良いとわかる。しかし薬は取る順序によって高橋くんの強さが変わってくる。ということは飲んだ薬のbitDPで、高橋くんの最大の強さを保持するのか?とわかる。しかしどのように遷移するのだろう?最後に飲む薬を集合の中から1つ選んだとして、それ以外を先に飲んで、それを最後に飲むことができるかどうかわからないじゃないか。ということでdpのついでに次飲める薬も保持しておいた。次飲めるものに入ってるのだけ、最後の薬として選択する。(でも解説に出てこないので、この処理が必要なのかよくわからん。)DFSしつつ、heapqで一番弱い敵から倒していくという処理を、毎回やり直すので、間に合わなそうと思ってしまうが、N = 500で、薬は10個なので、いける。orange 2023-09-09
G - Counting Shortest Paths
x ★ おもしろい。N = 200000で完全グラフで最短パスということで、普通のBFSで最短パスを求めるとO(N^2)で無理だが、削除する辺がM = 200000ということで、こちらに注目するといけるらしい。BFSするとき、通った頂点(距離が求まった頂点)を保持しておいて、処理を進める方法しかやったことなかったが、通ってない頂点を保持しておいて、どんどん減らしていくという方法があるらしい。目からウロコで、1度もそうやろうと思ったことはなかった。通常、最短パスの個数を数えるには、距離がd-1の頂点のうち、隣接している頂点から遷移していくが、O(N^2)を避けるため、これも辺を削除して隣接していない頂点の遷移を、合計から引く方法で処理することで、計算量を減らすことができる。2つめのトリックは自分で考察しているときに気づいたが、1つ目は、これまでやってきたBFSのやり方の思い込みが強すぎて、全く思いつかなかった。でもある意味典型だと思うので、身につけられてよかった。yellow #BFS 2023-09-09
import sys
from collections import deque, defaultdict
mod = 998244353
N, M = map(int, input().split())
G = [set() for _ in range(N)]
for _ in range(M):
u, v = map(int, input().split())
u, v = u-1, v-1
G[u].add(v)
G[v].add(u)
S, T = 0, N-1
notused = set(range(1, N))
dist = [-1]*N
dist[0] = 0
q = deque([0])
while q:
cur = q.popleft()
remove = set()
for nex in notused:
if nex not in G[cur]:
q.append(nex)
dist[nex] = dist[cur] + 1
remove.add(nex)
notused -= remove
if dist[T] == -1:
print(-1)
sys.exit()
d2v = [[] for _ in range(dist[T]+1)]
for v in range(N):
if dist[v] <= dist[T]:
d2v[dist[v]].append(v)
dp = [0]*N
dp[S] = 1
for d in range(dist[T]):
nd = d + 1
sumprev = 0
for prev in d2v[d]:
sumprev = (sumprev + dp[prev]) % mod
for v in d2v[nd]:
dp[v] = (sumprev - sum(dp[prev] for prev in G[v] if dist[prev] == d)) % mod
print(dp[T])AtCoder Beginner Contest 320
ABCDE、5完。パフォーマンス1593で過去ベスト4なので割りと良かったらしい。何が良かったのかはわからない。Fは、両側から同時にDPだろうということまで方針はあってたが、かなりややこしく、コンテスト時間内に詰めきれなかった。こういうのを時間内に解ききりたい。終了後ACしたが、大変だった。
C - Slot Strategy 2 (Easy)
o こういうの解説の方針でさっと解けるようになったのも、何かしらの成長と言えるか。一番最短で、というのを、はじめから最短になるようなアルゴリズムを考えるのではなく、全パターン試せばいい。しかし単に計算量を意識するようになるということかもしれない。間に合うからこれでいい。と思っているだけなので。 2023-09-16
M = int(input())
S = []
for _ in range(3):
x = list(map(int, list(input())))
S.append(x*3)
ans = INF = 1000
for n in range(10):
for perm in [(0,1,2), (0,2,1), (1,0,2), (1,2,0), (2,0,1), (2,1,0)]:
sel = 0
i = 0
while i < 3*M:
if S[perm[sel]][i] == n:
sel += 1
if sel == 3:
ans = min(ans, i)
break
i += 1
print(ans if ans != INF else -1)F - Fuel Round Trip
x ★ 往復を同時にDP。その方針で考えていたが複雑すぎてコンテスト中に考えきれず。終わったあとも大変だった。進むのと戻るのを同時にって映画「テネット」みたいで混乱してしまう。現実の感覚が抜けないとうまくいかないかも。でも競プロの中ではそういうことはよくあることw いかに、余計な情報を遮断して、純粋なロジックの世界に持ち込むか?往路は燃料買ったあと、復路は買う前、なんだけど、買う前=後ろから見たら買ったあとなんだよな。なんか実行時間長いのが気になる。 yellow #DP 2023-09-16
INF = 10**10
N, H = map(int, input().split())
X = [0] + list(map(int, input().split()))
CF = [(0, 0)]
for _ in range(N-1):
CF.append(tuple(map(int, input().split())))
# [i] [a] 往路の燃料 [b] 復路の燃料 での最小コスト
dp = [[INF]*(H+1) for _ in range(H+1)]
for b in range(H+1):
dp[H][b] = 0
for i in range(1, N+1): # 1-N
ndp = [[INF]*(H+1) for _ in range(H+1)]
pi = i - 1
d = X[i] - X[pi]
if d > H:
dp = ndp
break # 絶対無理
for pa in range(d, H+1):
a = pa - d # 燃料がd減る
for pb in range(H-d+1):
b = pb + d # 燃料がd増える
ndp[a][b] = min(ndp[a][b], dp[pa][pb])
if i == N:
dp = ndp
break
c, f = CF[i]
dpa = [[INF]*(H+1) for _ in range(H+1)] # 往路で買う場合
for b in range(d, H+1):
for a in range(H-d+1):
na = min(H, a + f)
dpa[na][b] = min(dpa[na][b], c + ndp[a][b])
for nb in range(H): # ここムズい
b = min(H, nb + f)
for a in range(H-d+1):
ndp[a][nb] = min(ndp[a][nb], c + ndp[a][b])
for a in range(H+1):
for b in range(H+1):
ndp[a][b] = min(ndp[a][b], dpa[a][b])
dp = ndp
ans = INF
for a in range(H+1):
ans = min(ans, dp[a][a])
print(ans if ans != INF else -1)G - Slot Strategy 2 (Hard)
x フローと2分探索。典型的な見た目をしつつも、全リールN個まで見ればいいよね(全部かぶってても収まるのだから)ということに気づいて辺の数を減らす必要があり、そういうことにも気がつけるようになりたい。 orange #最大流 2023-09-16
N, M = map(int, input().split())
S = [[[] for _ in range(N)] for _ in range(10)]
for i in range(N): # slot i
for j, x in enumerate(map(int, input())):
if len(S[x][i]) < N:
S[x][i].append(j)
ans = N * M + 1
for x in range(10):
possible = True
for i in range(N): # slot i
if not S[x][i]:
possible = False
break # impossible
j = 0
while len(S[x][i]) < N:
S[x][i].append(S[x][i][j] + M)
j += 1
if not possible:
continue
allj = set()
for i in range(N):
for j in range(N):
allj.add(S[x][i][j])
t2j = {}
for j, t in enumerate(allj):
t2j[t] = j
START, GOAL = 0, N + len(allj) + 1 # X to Y
l, r = -1, N * M
while l + 1 < r:
m = (l + r) // 2
mf = MF(GOAL + 1)
for i in range(1, N+1):
mf.add_edge(START, i, 1)
for i in range(N+1, GOAL):
mf.add_edge(i, GOAL, 1)
for i in range(N):
for t in S[x][i]:
if t > m:
break
mf.add_edge(i+1, N+1+t2j[t], 1)
if mf.mf(START, GOAL) == N:
r = m
else:
l = m
ans = min(ans, r)
print(ans if ans < N*M+1 else -1)AtCoder Regular Contest 165
AB、2完。Cも方針はあっていたけど、ABで時間使いすぎて、間に合わず。Cができればいいパフォーマンスが望めたはずだが、つらい。それでもRating微増(1344 -> 1354)でHighest更新。ていうか頭が疲れ切ってた。昨日のABC320のFとか、赤DiffのABC261 GをなんとかACして、ちょっとだけ喫茶店で気晴らししてからのコンテスト。昼寝したかったけど余裕なし。ABC261 Gはきつかった。
B - Sliding Window Sort 2
o 時間かかって102分で提出したものがなんとノーペナAC。手こずって時間的にこりゃやべぇ、ここからWA出てギリギリまでつらいデバッグかぁ?という流れが見えて、トホホという感じだったので、通ったときは嬉しかった。AをACした時点では1300位台で、出遅れたが、Bを102分でACしたタイミングで900位台に上がったので、これだけで、Bが解けなかった人たちを400人追い抜けたらしい。解説読む気が起きないけど、高々2つに候補を絞り込めるので、それらを比較してでかい方を回答、っていう部分は同じで、ぼくもそうなった。でもそこまでになぜかセグ木とか使って大事になってたが、まあいい。 light blue 2023-09-17
import sys
N, K = map(int, input().split())
P = list(map(int, input().split()))
segt = SEGT(N+1)
for i in range(N):
segt.set(i, P[i])
count = 0
countmax = 0
inc = [0]*N
for i in range(N-1):
if P[i] < P[i+1]:
count += 1
countmax = max(countmax, count)
else: # P[i] > P[i+1]
inc[i-count] = count # from [i-count] to [i], count + 1 numbers
count = 0
if countmax >= K-1:
print(*P)
sys.exit()
IPOSI = []
for i in range(max(0, N-2*K+1), N-K):
count = inc[i]
if count == 0:
continue
minright = segt.query(i+count+1, i+K)
for j in range(i, i+count+1):
if minright < P[j]:
IPOSI.append((i, j))
break
Q = P[:N-K] + list(sorted(P[N-K:]))
if IPOSI:
IPOSI.sort(key=lambda x: -x[1])
i, _ = IPOSI[0]
cand = P[:i] + list(sorted(P[i:i+K])) + P[i+K:]
if Q > cand:
print(*Q)
else:
print(*cand)
else:
print(*Q)C - Social Distance on Graph
o 残り20分でCを考えだしたが、2分探索で、X未満のエッジだけで2部グラフを作るということまで時間内に考えていて、あとはその2部グラフ内で同じ色同士がX未満にならないかチェックするというところだけだった。結構惜しい。でもややこしいBを短時間で解けることも含めてパフォーマンスにつながるのだから、仕方ない。もうちょっと、って思うことが多いし、それによって自分のRating程度のパフォーマンスに落ち着く。いずれ、なんとかブレイクスルーしたい。下に2分探索使わない方法へと続く。
N, M = map(int, input().split())
G = [[] for _ in range(N)]
maxw = 0
for _ in range(M):
a, b, w = map(int, input().split())
a, b = a-1, b-1
G[a].append((b, w))
G[b].append((a, w))
maxw = max(maxw, w)
minsum = [10**10]*N
for v in range(N):
G[v].sort(key=lambda x: x[1])
if len(G[v]) >= 2:
minsum[v] = G[v][0][1] + G[v][1][1]
l, r = 0, 2*maxw+1
while l + 1 < r:
m = (l + r) // 2
used = [-2]*N # -1 or 0 are used
NG = False
for v in range(N):
if used[v] > -2 or G[v][0][1] >= m:
continue # skip v
stack = [v]
used[v] = 0
if minsum[v] < m:
NG = True
break
while stack:
cur = stack.pop()
for nex, d in G[cur]:
if d >= m:
break
if used[nex] == used[cur]:
NG = True
break
if used[nex] == -2:
if minsum[nex] < m:
NG = True
break
stack.append(nex)
used[nex] = ~used[cur]
if NG:
break
if NG:
break
if NG:
r = m
else:
l = m
print(l)★ DFSとかせずにUnion-Findを使って2部グラフ判定ができるらしい。それを使うと、重みが小さい順に辺を追加していって、2部グラフを作れなくなる重みを1回で調べられる。2部グラフというのは、2色で隣同士の頂点の色が全部異なるグラフである。赤青とする。頂点XはX赤とX青に分裂させる。頂点Aと頂点Bが隣接する時、A赤とB青、A青とB赤をつなぐ。もしA赤とA青が連結していなければ、2部グラフである。確かに、A赤とA青がつながってないってことは、全体として矛盾が起きてないということ。どのようなパスを通っても偶数本の辺を通過するなら、A赤はA赤にしか繋がらない。Union-Findなので、隣接リスト作らず、辺の情報だけでいけるというメリットもある。(今回はどっちもいるが。)で、この問題をどう解くかというと、理解に苦しんでしまったが。まず辺の重みでソートして短い順にUnion-Findしていく。重みWのところで2部グラフが崩れたとする。W未満の長さの辺で2部グラフが作れるということなので、W未満の辺の両端の頂点はすべて別の色に塗り分けることができる。よって同色隣接頂点間の重みは最大W以上にできる。Wの辺で必ず両端が同色のものが発生するので、W+1以上にはできない。Xの候補はWとなる。全部追加しても2部グラフであれば、この時点でXの候補は∞。次に同色頂点間に2辺ある場合の重みを考えるが、全頂点で2部グラフを作れた場合(現在のXの候補が∞の場合)は、明らかに同じ色の頂点間のパスの重みの最小値は、2辺からなるパスの重みの最小値を確認すれば良い。Xの候補がWのとき、W以上の辺を含むパスの重みはその時点で、W以上なので考えなくても良い。よってW未満の辺で作られた2部グラフの中の2辺からなるパス(これは同一色の頂点間のパスとなる)の重みの最小値がW未満だった場合、Xはその値に更新しなければならない。が、それが存在するのであれば、結局2辺からなるパスの重みの最小値である。総合すると、2部グラフを作れなくなるWの値と、2辺からなるパスの重みの最小値の、小さい方がこの問題の答えとなる。解説にサラッと書いてあるが、現在のぼくの頭では、これを短時間で考え抜くのは無理だ。というか、整理するのに苦労した。よって、2分探索を使ったほうがむしろ見通しが良い。blue #グラフ #2部グラフ判定 #UnionFind #超頂点 2023-09-17
N, M = map(int, input().split())
uf = Union(2*N)
G = [[] for _ in range(N)]
edges = []
for _ in range(M):
a, b, w = map(int, input().split())
a, b = a-1, b-1
edges.append((a, b, w))
G[a].append((b, w))
G[b].append((a, w))
ans = 10**10
for v in range(N):
if len(G[v]) >= 2:
G[v].sort(key=lambda x: x[1])
ans = min(ans, G[v][0][1] + G[v][1][1])
edges.sort(key=lambda x: x[2])
i = 0
while i < len(edges):
a, b, w = edges[i]
uf.unite(a, b+N)
uf.unite(b, a+N)
if uf.same_tree(a, a+N):
ans = min(ans, w)
break
i += 1
print(ans)AtCoder Beginner Contest 321
ABCDE、5完、ウォッチしてる自分より上の人達が結構Eを解けてなかったので、うれしい。そういうことが増えてきたと感じているし、さらにそういうことが増えていくと実力がついたことを実感できるだろう。FはEと同程度のDiffらしいが、ぼくにはFが難しく、今回勉強になってよかった。典型と思われるので、解かれていると思う。
C - 321-like Searcher
o 何個くらいあるのかな?と考えると0から9までの数字の部分集合を作って並べた数字なので、約2^10とわかる。少ないので全部作ってソートしてK番目を答えれば良い。桁数でループしてcombinationsを使って生成したけど、解説ではbit全探索をしていた。brown 2023-09-23
from itertools import combinations
K = int(input())
all_ = list(range(1, 10))
for keta in range(2, 11):
for combi in combinations(range(10), keta):
all_.append(int(''.join(map(str, reversed(combi)))))
all_.sort()
print(all_[K-1])D - Set Menu
o 主菜副菜の数、N = M = 200000。O(N Log N)。主菜の値段ごとに、副菜がいくら以上で合計Pを超えるか決まるので、副菜を値段でソートしておけば、2分探索で位置確定、副菜の累積和も作っておけばO(1)で計算できる。green #累積和 #2分探索 2023-09-23
import bisect
from itertools import accumulate
N, M, P = map(int, input().split())
A = list(map(int, input().split()))
B = list(map(int, input().split()))
A.sort()
B.sort()
Baccu = list(accumulate(B))
ans = 0
for a in A:
ib = bisect.bisect_left(B, P-a)
if ib != 0:
ans += ib * a + Baccu[ib-1] + P * (M - ib)
else:
ans += P * M
print(ans)E - Complete Binary Tree
o 残り3分でAC。この問題が結構解かれてなかったのでACできてよかった。最初、2分木を登ってから降りるケースを考慮できてなくて、修正に時間がかかってしまった。最初の方針が間違っていると、修正に時間がかかる気がする。思い込みがコードに盛り込まれていて、なかなか抜けられないのだと思う。最初から正しい方針で考察できていると、ストレートなロジックになってミスが入りにくい。やはり直すのがしんどい。青Diffとは、コンテスト中に解けた記憶が少ないので喜ばしい。2分木といえばセグ木のアルゴリズムを理解する過程で馴染みがあるので、とっつきやすいというのがあり、そういうのも苦労したことが役に立つ。深さd、下に進んだ範囲は、左側はx->2xを繰り返して計算、右側はx->2x+1を繰り返して計算できる。左側よりNの方が大きければ、数えればいい。登って降りるパターンは、登ることによって、距離dを減らしていって、逆側に降りて、同じ方法で数えられる。blue 2023-09-23
F - #(subset sum = K) with Add and Erase
x ★ 数字が与えられて、そのなかからいくつか選んで総和をKとする方法の数。典型的ナップサックDPだが、数字を減らすという処理が加わったもの。自力では全く思いつかなかったが、減らすのもDPでいけるらしい。DP[i]は、総和iとなる総数とする。xをなくすことを考える。無くす前の時点を考えると、DP[i+x]の中には、必ずDP[i]に含まれるパターンのうち、xを使っていなかったパターンに、xを追加したパターンが必ずすべて含まれていることがわかる。そのうえ、xを使うパターンはこの作り方ですべてだということもわかる。さらに、DP[0]からDP[x-1]までは、必ずxを使っていない。よって、DP[x]からDP[2x-1]に対して、それぞれDP[0]からDP[x-1]を引くと、xを使っていないパターンの総数だけが残ることがわかる。xを使っていないパターンだけになったDP[i]を、さらにDP[i+x]から引くことによって、全部xを使っていないパターンの数だけにできる。iが小さい順に処理すればよい。初めて見たので難しかったが、引く方も典型なのだろうと思う。blue #サップサックDP 2023-09-23
M = 998244353
Q, K = map(int, input().split())
dp = [0]*(K+1) # 0-K
dp[0] = 1
ans = []
for _ in range(Q):
pm, x = input().split()
x = int(x)
if pm == '+':
for i in range(K-x+1)[::-1]:
dp[i+x] = (dp[i+x] + dp[i]) % M
else:
for i in range(K-x+1):
dp[i+x] = (dp[i+x] - dp[i]) % M
ans.append(dp[K])
print(*ans, sep='\n')G - Electric Circuit
x ★ いろいろとポイントのある問題で勉強になった。連結成分の個数の期待値を求める = ある部分集合を考えたときに、それが1つの連結成分となる確率の和を求める。この言い換えか。期待値の線形性という性質を使っているらしい。最初ARC163 Dを思い出してた。あれは強連結成分の分割位置をカウントすることで強連結成分の個数を数える主客転倒だった。さて、部分集合が1つの連結成分になる場合の数をどのように数えるか?部分集合内ですべての端子間をつなぐこと、さらに部分集合内で複数の連結成分に分かれていないことが必要。1つ目の、すべての端子間を部分集合内でつなぐ方法は、端子数の階乗で求められる。2つ目が難しい。集合内で分割しているつなぎ方を重複なく数えるには、ある部品Aに注目し、それを含む部分集合が1つの連結成分であるつなぎ方を数えればいい。そうすれば、Aを含む連結成分が異なるパターンをすべて数えられるので、数え方に重複が発生しない。よってある集合が連結成分になるつなぎ方が数えられたので、1つの連結成分になる確率は、「集合内での1つの連結成分になるつなぎ方 x 集合外のすべてのつなぎ方 / すべてのつなぎ方」で求められるので、その合計が答えとなる。現時点、実行時間がPython勢最速でうれしい。orange #bitDP #期待値 #期待値の線形性 2023-09-23
mod = 998244353
N, M = map(int, input().split())
fact = [1]*(M+1)
for i in range(1, M+1):
fact[i] = fact[i-1] * i % mod
i2b = [1]
b2i = {1: 0}
for i in range(1, N):
nex = i2b[-1] * 2
i2b.append(nex)
b2i[nex] = i
R = [0]*N
B = [0]*N
for i in map(int, input().split()):
R[i-1] += 1
for i in map(int, input().split()):
B[i-1] += 1
dp = [0]*(2**N) # 1つの連結成分になるbit内つなぎ方
rsum = [0]*(2**N)
bsum = [0]*(2**N)
for bit in range(1, 2**N):
if bit.bit_count() == 1:
i = b2i[bit]
rsum[bit] = R[i]
bsum[bit] = B[i]
if R[i] != B[i]:
continue
dp[bit] = fact[R[i]]
else:
fix = bit & -bit # watch subset including this
rsum[bit] = rsum[bit-fix] + rsum[fix]
bsum[bit] = bsum[bit-fix] + bsum[fix]
if rsum[bit] != bsum[bit]:
continue
count_div = 0
left = bit - fix
sub = left
while sub:
sub = (sub - 1) & left
# don't see when sub + fix = bit
con = sub + fix
if rsum[con] == bsum[con]:
count_div = (count_div + dp[con] * fact[rsum[bit - con]]) % mod
dp[bit] = (fact[rsum[bit]] - count_div) % mod
ans = 0
inv = pow(fact[M], mod-2, mod)
all_ = 2**N - 1
for bit in range(1, 2**N):
if dp[bit] != 0:
ans = (ans + dp[bit] * fact[rsum[all_-bit]] * inv) % mod
print(ans)AtCoder Beginner Contest 323
3連休初日、歯が痛い中臨んだABC323、6完で3度目の青パフォ、過去ベスト3のパフォーマンスだった。7問目の行列木定理は激ムズなので、698位だけど、17位の人と解いた問題は同じ。同じの解いてもスピードでこんなにパフォーマンス変わるんだよなぁ。
B - Round-Robin Tournament
o 「総当たり戦で勝った試合数が多いほうが順位が上であり、勝った試合数が同じ場合は、プレイヤーの番号が小さいほうが順位が上となります。」シンプルに書けた。2023-10-07
N = int(input())
A = []
for i in range(1, N+1):
A.append((input().count('x'), i))
A.sort()
print(*[i for l, i in A])D - Merge Slimes
o 本番中、シミュレーションで解いた。heapqで一番小さいスライムを管理して、数もdictで管理して、どんどん合成していく。制限時間3秒のところ、2765msでギリギリだった。最適な解法でないのは明らかだった。
import heapq
from collections import defaultdict
N = int(input())
pq = []
memo = defaultdict(int)
count = 0
for _ in range(N):
S, C = map(int, input().split())
memo[S] += C
count += C
heapq.heappush(pq, S)
while pq:
s = heapq.heappop(pq) # smallest slime
c = memo[s]
chalf = c // 2
count -= chalf
if chalf > 0 and 2*s not in memo:
heapq.heappush(pq, 2*s)
memo[2*s] += chalf
print(count)解説では、合成すると、そのサイズのスライムが必ず1つになることと、合計のサイズが変化しないことから、2進数表現したbit数が最後のスライム数であるとしている。相当賢いと思った。この解法思いついて最初からやるのは相当だと思う。171msになった。2023-10-07
from collections import defaultdict
N = int(input())
groups = defaultdict(int)
for _ in range(N):
S, C = map(int, input().split())
v = 1
while S % 2 == 0:
v *= 2
S //= 2
groups[S] += C * v
ans = 0
for v in groups.values():
ans += v.bit_count()
print(ans)AtCoder Regular Contest 166
AB、2完。Aがバグって1時間以上かかった。Bは30分くらいでできたけど、残り20分。Cはおもしろい問題だったけど、閃かなかった。Dはコンテスト後自力AC。DはCのような閃きはいらず、Aよりもやりやすいくらいに感じた。ARCってA、Bあたりにうまく実装しないと沼りかねない問題が配置されてる気がする。このあたりをミスらずに短時間でACできるかで、点数が変わってくるなぁと思う。ていうか3連休2日目なんだけど、休み中、寝れないほど歯が痛くなり、本当に死にそうなんだった。昨日のABC323に続き、歯の激痛に耐えながらの参加だけど、コンテスト中は集中しすぎて痛みを忘れるのは、本当に驚くべきこと。
A - Replace C or Swap AB
o 考察すると、Cに置き換える操作はないので、XがAかBで、YがCという位置があるとNG、XがCでYがCのところは触ってはいけないとわかる。そこまでわかると、XがC、YがCの部分で分割した残りの部分ごとに、個別にチェックすればよいとわかる。ABをBAに置き換えるという操作で、AとBの個数は変わらない。また、この操作でAを後ろに好きなだけ移動できることがわかる。よって、C-Cを除いた部分ごとに、XのCをYのAかBに置き換えて、その部分のAとBの個数をそろえ、Aを後ろに移動するという操作が可能。ということは、X側の部分とY側の部分を前から1文字ずつ調べたときに、常にX側のAの個数がY側のAの個数以上であれば、XとYを一致させることができる。これを最初1つのループ内で全部処理しようとして、バグ修正に時間がかかった。最終的にコードを消してC-Cを除いた部分の処理を別関数に分離して書き直したら一発でACできた。1回のループで処理すると定数倍が1になるが、たとえば、同じ文字列を3回なぞっても時間内に収まりそうならば、わかりやすく、バグが入りにくい実装方針にした方がいい。下のコードは、連続する部分をチェックするコードの部分のみだが、冗長だが明確でミスりにくく良いと思う。XのAがYのAより前にあるというのを、Aをカウントしていけば確認できるというのは、この関数を書き出して気づいた。最初もっとややこしい実装をしてしまっていた。2023-10-08
def check(x, y):
n = len(x)
countax = 0
countay = 0
for i in range(n):
if x[i] == 'A':
countax += 1
if y[i] == 'A':
countay += 1
if countax > countay:
return False
adda = countay - countax
for i in range(n):
if x[i] == 'C':
if adda > 0:
x[i] = 'A'
adda -= 1
else:
x[i] = 'B'
countax = 0
countay = 0
for i in range(n):
if x[i] == 'A':
countax += 1
if y[i] == 'A':
countay += 1
if countay > countax:
return False
return TrueB - Make Multiples
o あまり0のとき、操作不要ってのを処理できてなくて1ペナ。この問題も、方針が立って、実装がシンプルにできるか?というところ。たとえば、どれかをaの倍数にする、bの倍数にする、cの倍数にするという組み合わせでの最小操作数を見つける時、その3つは異なる数字である必要があるが、どのように書くとわかりやすいだろうか?操作回数が小さい順にソートしたものを3つ目まで調べれば十分とわかる。よってa, b, cから3つ目までのどれかを選んだ組み合わせが必要。itertools.productでrepeat=3とすると、組み合わせを全列挙できる。選んだものが異なっている場合を答えの候補として計算する。lcm(a, b)とかlcm(a, b, c)とかに対しても操作回数のリストが必要だが、この辺はベタ書きで仕方ないかなと思った。2023-10-08
ids = [0, 1, 2]
if N == 2:
ids = [0, 1]
if N == 1:
ids = [0]
for prod in product(ids, repeat=3):
i, j, k = prod
if a_[i][1] != b_[j][1] and b_[j][1] != c_[k][1] and c_[k][1] != a_[i][1]:
ans = min(ans, a_[i][0] + b_[j][0] + c_[k][0])C - LU / RD Marking
x 気づかなかった。おもしろい。なんか気づいたらシンプルになる系のような気がして、狙ってたが、閃かなかった。解説のように、ななめに分解すると、それぞれの部分で独立にパターン数を計算できる。n個から連続する2つをいくつか選ぶ方法の数。左端を選ぶ場合、F(n-2)通り。選ばない場合F(n-1)通り。よって、F(n) = F(n-1) + F(n-2)でフィボナッチ数になるらしい。なんと。フィボナッチ数が出てくるとは。各部分のパターン数の積が答え。テストケース数が20万、グリッドのH, Wが100万。なので、毎回積を計算していると間に合わない。累積積を事前に計算しておく。256msで80くらいのPython提出の中で現在6番目でうれしい。#累積積 #フィボナッチ数 2023-10-08
mod = 998244353
maxhw = 1000000
maxe = 2000001
fib = [0]*(maxe+1)
fib[1], fib[2] = 1, 2
for i in range(3, maxe+1):
fib[i] = (fib[i-1] + fib[i-2]) % mod
prd = [1]*(maxhw)
prd[0] = 2
for i in range(1, maxhw):
prd[i] = prd[i-1] * fib[2*(i+1)] % mod
T = int(input())
ans = []
for _ in range(T):
H, W = map(int, input().split())
if W < H:
H, W = W, H
# W >= H
cur = prd[H-1] * prd[H-1] % mod
ans.append(cur * pow(fib[H*2+1], W-H, mod) % mod)
print(*ans, sep='\n')D - Interval Counts
o これは自力でいけた。dequeにLの位置と個数のリストを管理する実装方針はなかなかいい判断と思える。2023-10-08
from collections import deque
INF = 10**9
N = int(input())
X = list(map(int, input().split()))
Y = list(map(int, input().split()))
q = deque([])
q.append([-INF, Y[0]])
ans = INF
for i in range(1, N):
if Y[i-1] == Y[i]:
continue
if Y[i-1] > Y[i]:
posi = X[i] - 1
rem = Y[i-1] - Y[i]
while rem > 0:
ans = min(ans, posi - q[0][0])
if q[0][1] <= rem:
rem -= q[0][1]
q.popleft()
else: # q[0][1] > rem
q[0][1] -= rem
break
else: # Y[i-1] < Y[i]
q.append([X[i-1] + 1, Y[i] - Y[i-1]])
print(ans if ans < INF else -1)AtCoder Beginner Contest 324
4完で失敗。Eをとんでもない読み間違いをして崩壊した。なんでこんなにボケまくってるの?先週は歯の激痛に加えて前日の不摂生でコンディション最低だったのに、成績が良く、今回は歯の治療をしてスッキリして、木曜から酒を飲まずに早寝。それでダメってホント、ままならないものだな。
E - Joint Two Strings
o 問題を読み間違えた。「SiとSjをこの順に連結して得られる文字列は、Tを(連続とは限らない)部分列として含む。」という部分を「SiとSjをこの順に連結して得られる文字列は、Tに連続する部分列として含まれる。」と読み間違えた。どっちがどっちに含まれるかが逆だし、連続とは限らないと書いてあるのに連続と読んだ。むちゃくちゃ。その勘違いにコンテスト終了まで気づかなかった。どうなっとんねん。で、両側からAho-Corasickやるのか?と思いがんばるも、流石に慣れてなくて短時間で実装できず、Fやった方がいいか?みたいな動揺隠しきれず、崩壊。まあこの機会にAho-Corasick少しでも短時間で実装できるようにちゃんと見直そうと思う。まずは問題文を正しく読んだ方から。これはこれで実装に手間取ってバグったのだった。最終的にACした実装は以下の通りスッキリしており、これを最初からできなければという話。Tの前から何文字、後ろから何文字の最長部分列を含むかを計算しておいてつき合わせれば良いんだけど、最初、最長部分列の最後の文字の、Tのインデックスを求めておいてつき合わせようとしてて、バグった。文字数の方がシンプルになってバグりにくいんだよなぁ。あと後ろから調べる時にreverseした文字列で処理したら同じ方針でできて楽。Tのインデックスを求めようと思うと、reverseしたらややこしくなるし、そのためにreverseせずに処理しようと思うと後ろからループを回さないといけない。よって、インデックスを求めるのではなく、reverseして文字数を数えるという方針はすごく理にかなっている!こういうの最初の方針で気づけるのが競プロ強いよなぁ、と。
from collections import defaultdict
N, T = input().split()
N = int(N)
T = list(T)
Trev = list(reversed(T))
mae = [0]*(len(T) + 1)
ato = [0]*(len(T) + 1)
for _ in range(N):
S = list(input())
count = 0
j = 0
for c in S:
if c == T[j]:
count += 1
j += 1
if j == len(T):
break
mae[count] += 1
count = 0
j = 0
for c in reversed(S):
if c == Trev[j]:
count += 1
j += 1
if j == len(T):
break
ato[count] += 1
for j in range(len(T))[::-1]:
ato[j] += ato[j+1]
ans = 0
for m in range(len(T) + 1):
left = len(T) - m
ans += mae[m] * ato[left]
print(ans)さて、勘違いしたAho-Corasickを使う方もいつかのために考察しておこう。頭に定着してなくて、短時間で全然実装できず、動揺しまくってコンテスト全体が崩壊したので。Trie木の各ノードが、最も長いSuffixと一致するノードへのリンクを持っている。この構築方法まで理解していなければ、問題が解けなかったりする。どうやって構築するか?1文字目のノードはすべてrootノードにリンクする。リンクが確定したノードの子要素のリンクを順次求めていくことができる。子要素のリンク第一候補は、その親(すでにリンク先が確定)のリンク先の子要素である。同じ文字の子要素がないばあい、さらにリンク先を調べる。最後まで見つからなければrootにリンクするという具合で、全部のリンクを確定できる。文字列Tを1文字目から順次調べるには、どのように処理するか?currentをrootとする。1文字目がrootの子に存在するか調べる。なければTの次の文字へ。rootの子に存在するところでcurrentをその子ノードに移動。Tの次の文字がcurrentの子に存在すればcurrentをその子に移動。なければリンク先の子に存在するか調べる。リンク先にもなければそのリンク先の子にあるか?と繰り返す。rootの子に見つからなければcurrentをrootにして、その文字はスキップ。という具合に処理を続ける。なので、構築処理順と、検索処理順が似ていると言える。すべての部分文字列をO(N)で見つけられる。まじか?考えていてちょっと疑問なのが、リンクに飛んだ時、それより長い文字列と実は一致していてそれを見逃すことはないのか?ということ。Aho-Corasickの根幹に関わることなので、見逃すようでは使い物にならないのだが、なんで見逃さないの?と。見逃す可能性として頭の中で思い浮かぶのは、ジャンプ先の文字列の前の文字列が一致するパスがTrie木に存在した場合だが、それはありえない。ジャンプ先にリンクされたより長い文字列は、当然ありうる。そっちとTが実は一致しているということはありえない。なぜならジャンプ元の文字列も、そのジャンプ先にリンクされた別の長い文字列も、Trie木上でべつのパスである。よって別の文字列が実は一致しているということはありえない。つまりこのアルゴリズムを通じてTrie木に登録された単語を見逃さずにすべて検出できる。さて、このぼくが誤読した問題を解くためには、Tのインデックスiで終端する単語数を数える必要がある。その位置で終端する単語数を瞬時に答えるためにはAho-Corasickを構築しながら、そのノードで終端する単語の数を、累積和的にノードが保持しておく必要があるだろう。構築しながらリンクをたどる時、リンク先の終端単語数を、加えればよいはずだ。キューで管理して浅い順にリンク確定していくから、リンク先の子はすでにリンク構築済みで、単語数確定しているよね。。。green #Aho-Corasick 2023-10-15
F - Beautiful Path
x ★ 中身は食塩水の問題という典型らしい。その食塩水問題も2分探索で解く問題だったりするので、知っている人にとってはこの問題が2分探索であることに驚きはないのかもしれない。かなりすごい発想だが。美しさの総和をコストの総和で割る=食塩の総和を食塩水の総和で割る=濃度。Σb/Σc>=Xという式を変形してΣ(b-cX)>=0。濃度X以上であることが、b-cXの総和が0以上であることに結びつく。bとcを別々に足して、より濃度が高くなるものなど見通せないのに、X以上であることはb-cXの和で確認でき、b-cXの和がでかけりゃでかいほどいいという問題に帰着して、DPできる。b-cXというのは、意味的には、濃度Xに必要な食塩よりどれだけ余分にあるか?ということである。辺の数M=200000で1回のDPのコストがO(M)にすぎないので、誤差10^-9以下になるまで2分探索する余裕がある。blue #食塩水 #DP 2023-10-14
N, M = map(int, input().split())
G = [[] for _ in range(N)]
for _ in range(M):
u, v, b, c = map(int, input().split())
u, v = u-1, v-1
G[u].append((v, b, c))
l, r = 0.00001, 100000
INF = 10**10
TOL = 10**-10
while l + TOL < r:
m = (l + r) / 2
dp = [-INF]*N
dp[0] = 0
for u in range(N):
if dp[u] != -INF:
for v, b, c in G[u]:
dp[v] = max(dp[v], dp[u] + b - c * m)
if dp[N-1] >= 0:
l = m
else:
r = m
print(l)AtCoder Regular Contest 167
50分でノーペナ2完、515位、パフォーマンス1847という過去最高の成績で、ようやくRating1400超え、3級昇格した。2週連続のABC、ARC。初週にまさかの歯痛でどうなるかと思ったが、この4試合目で最高の成績を収めて良い終わり方ができた。しかし、Cに70分残っていて解ききれなかったのは残念だった。このコンテスト、C、Dともに、黃コーダーでも30%しか解けてなかったが、コンテスト後にやっていて、どちらもむちゃくちゃいい問題だと思った。こういうのをコンテスト中にスッキリ解ききりたいものだ!そういえばBを提出した時点で順位を見たら400位台で、こんな順位初めて見た!と興奮した。最終的に500位以下に下がってしまったけど。
A - Toasts for Breakfast Party
o ★ 無証明なので解説見ておいた方がいい。2023-10-15
B - Product of Divisors
o 50分で解けたおかげではじめてパフォーマンス1800超えて良かった。各素因数を0個以上でいくつ使うか?という全組み合わせの乗数を全部足して全約数の積が求まるので、と計算してたら答えの式まで導けた。998244353で割った値ってところで不安になったが、これでよかったらしい。奇数のときは1引いてから2で割れば割り切れる計算になる。ふ~。light blue #整数論 2023-10-15
import sys
def prime_factorization(n):
res = []
a = 2
while a*a <= n:
count = 0
while n % a == 0:
count += 1
n //= a
if count:
res.append((a,count))
a += 1
if n != 1:
res.append((n,1))
return res
mod = 998244353
A, B = map(int, input().split())
if B == 0:
print(0)
sys.exit()
res = prime_factorization(A)
inv2 = pow(2, mod-2, mod)
odd = True
if B % 2 == 0:
odd = False
if odd:
for p, x in res:
if x % 2 == 1:
odd = False
break
ans = B % mod
for p, x in res:
ans = ans * (x * B + 1) % mod
if odd:
ans -= 1
print(ans * inv2 % mod)C - MST on Line++
x ★ 主客転倒か?とまで気づいて、期待しながら取り組んでいたが、力尽きた。iの位置にaがあるとき、それが辺の重みとして使われる回数は?みたいな主客転倒。解説見て感動。コンテスト中に、Aに同じ数字があったらどうするんだろう?と悩んでたけど、勝手に順序つけてしまって区別して計算すれば辻褄が合う。こういうの見たことある気がする。コンテスト終了後、最小全域木を作るアルゴリズムを詰めきれずに解けなかったと思ってたけど、最小全域木を作る方法は、クラスカル法そのものであり、辺の重みが小さい順につないでいくだけだ。辺の重みがA[i]以下という時点で、「AをソートしたA[i]までの頂点を、閉路ができないようにつなぐ」という条件になる。A[i]が辺の重みとして使われる回数はA[i]まで使った辺の総数-A[i-1]までを使った辺の総数として求められる。それを求めるには、「i個の頂点を使って、距離K以下の頂点を、閉路を作らないようにつなぐ方法の数」を求める問題となる。閉路を作らないつなぎ方の辺の数は、簡単に数えられ、隣の頂点を見て距離がK以下ならつなげばいい。i個の頂点の間はi-1個あり、それぞれがK以下の距離になる場合の数はいくつですか?という問題に帰着される。信じられん。yellow #主客転倒 #数え上げ #最小全域木 2023-10-16
mod = 998244353
N, K = map(int, input().split())
COUNT_MAX = N
fact = [0]*(COUNT_MAX+1)
invfact = [0]*(COUNT_MAX+1)
fact[0] = 1
for i in range(1, COUNT_MAX+1):
fact[i] = fact[i-1] * i % mod
invfact[COUNT_MAX] = pow(fact[COUNT_MAX], mod-2, mod)
for i in range(COUNT_MAX-1, 0, -1):
invfact[i] = invfact[i+1] * (i+1) % mod
invfact[0] = 1
def choose(n, r):
return fact[n] * invfact[r] * invfact[n-r] % mod
A = list(map(int, input().split()))
A.sort()
ans = 0
prev = 0
for a in range(2, N+1):
temp = 0
for k in range(1, min(K+1, N-a+2)):
temp = (temp + choose(N-k, a-1)) % mod
temp *= a - 1
temp = temp * fact[a] % mod
temp = temp * fact[N-a] % mod
ans = (ans + (temp - prev) * A[a-1]) % mod
prev = temp
print(ans)D - Good Permutation
x ★ 生成するアルゴリズムはなんとなく思いつくが、ひとひねりしなければ、計算量を落とせなかった。おもしろい。順列の性質としてこれは盲点だった。順列をグラフ化すると複数の閉路になる。この問題における良い順列の条件はグラフが1つの閉路になること。2つの閉路をつなぐには、それぞれの閉路に所属するPiとPjをスワップすれば良い。それで2つの閉路は1つになる。よって、前から順に見て行って、別の閉路に属する一番小さい値の方が、小さいのであれば、それと貪欲にスワップして、閉路が1つになるまで続ければいいことがわかる。でもどれが別のグループに属していて、その中で最小の値がどれなのか?少ない計算量で言い当てる方法が全然思いつかない。この事実を使う。順列がx->Pxであるとき、Pxが含まれる閉路にxも含まれる。xもPxも同じグループの頂点。当たり前なのに全然見えない不思議…。なんだこれ。なので、前から順番に見て行って、x-1とxが別のグループに所属しているなら、xは別グループの「最小値である。」小さい順に見ていくのだから当たり前なのだった。スゲー!考察によって、前から順番にi番目をスワップして入れ替えているとき、このx-1とxが異なるグループに所属している最小のxは必ずiよりも大きいこともわかる。このあたり、自力でコンテスト中にそこまで考えられるのか?って疑問だわ。もしiが、xを超えて進んでいくとする。その場合、スワップが発生しないためには、i=x-1の時点でそれ以前のPiがすべてxより小さい必要がある。しかしその場合、Piにはx-1以下の数字しかないことになり、x-1までの数字のみで閉路を形成していることがわかる。しかし、閉路を全体で1つにしなければならないので、x-1のところでは、たとえ大きな数字とであろうとも、強制的にスワップしなければならない。だからこの手続きにおいて、iまで確定した時、iまでは必ず同じグループに所属した状態になっている。yellow #順列 #貪欲 2023-10-17
T = int(input())
for _ in range(T):
N = int(input())
uf = Union(N+1)
P = [0] + list(map(int, input().split()))
P_ = [0]*(N+1)
for i in range(1, N+1):
P_[P[i]] = i
for i in range(1, N+1):
uf.unite(i, P[i])
a = 2
for i in range(1, N+1):
while a <= N and uf.same_tree(a-1, a):
a += 1
# a-1 and a are in different groups
if a == N + 1:
break
if a < P[i] or uf.count[uf.find_root(i)] == i:
uf.unite(i, a)
j = P_[a]
P_[a], P_[P[i]] = i, j
P[i], P[j] = a, P[i]
print(*P[1:])AtCoder Beginner Contest 325
5完。ノーペナ60分、過去ベスト5のパフォーマンスで、5度目の青パフォとまずまずだった。Fに40分残ってたが解けなかったのは悔しい。単純なDPでは?と気づき、実装も時間内にバグ取れず、その後そのやり方は時間制限に間に合わないことがわかった。ちゃんと閃けばぼくでも気づける内容だったので、結局悔しい。勉強になった。このコンテスト終了時点でAccepted 702で700を通過。
C - Sensors
o 結構面倒な実装だなと思ったけど、AC時点で20分で、自分的には意外と早くて驚いた。解ければ良いので不必要な改善をしなくなったりしてるのが良いのかも。brown 2023-10-21
D - Printing Machine
o 解いた時点で50分くらい。結構難しいと思ったけど、周囲の人たちはやはりできている。でもこれが比較的早く解けたおかげでの青パフォだと思うし良かった。現在印字できる商品の中で、最も早く印字できなくなるものを、貪欲に印字してけば最適。これ、気づくの結構難しいと思うけど、過去に同様の発想見た記憶がある。貪欲シミュレーションを実装すれば良い。まあ、よくできたと思う。light blue #貪欲 2023-10-21
import heapq
N = int(input())
TD = []
for _ in range(N):
t, d = map(int, input().split())
TD.append((t, t+d))
TD.sort(key=lambda x: -x[0]) # 後ろのtが速い
INF = 10**20
pq = []
ans = 0
while TD:
t, d = TD.pop()
heapq.heappush(pq, d)
while TD and TD[-1][0] == t:
t, d = TD.pop()
heapq.heappush(pq, d)
now = t
nt = TD[-1][0] if TD else INF
while now < nt:
while pq and pq[0] < now:
heapq.heappop(pq)
if not pq:
break
heapq.heappop(pq)
ans += 1
now += 1
print(ans)F - Sensor Optimization Dilemma
x ★ 40分残ってて解けず。まずDPでいけることに気づくまで時間がかかった。それが不覚。コンテスト時間中に最初の方針で実装頑張ったが間に合わず、不覚。提出したらTLE、不覚。解説を見たが、やられたと思った。不覚。i番目の区間まで見てセンサー1と2の合計個数に対する最小コストというDPを考えていたが、よく考えたら個数が決まったらコストも決まるので、最小も何もない。状態K^2だと確かに、実行時間がちょっと厳しそうだなぁとわかっていたが、特定の区間に対するセンサー個数のペアが絞られるので、上手い具合に計算量が減って間に合うのかな?などと甘いことを考えていた。必要なのは、センサー1の個数に対するセンサー2の個数の最小値だ。ぼくの最初の方針だと、同じセンサー1の個数に対してセンサー2の個数が複数の状態を保持することになり、一番少ない時が最適に決まっているので無駄すぎるwww。「コストを最小にする」に条件反射的にコストを値として持つDPに飛びついてしまった。ひっかけかもしれない。書き直してむちゃくちゃ速くなった。あとループの順序の工夫も必要で、ある区間に対するセンサー1とセンサー2の個数を求める処理は1回だけやるループ順序にした方がいい。配る方のループの中で、毎回計算したら重い。そういうのも大事。blue #DP 2023-10-21
N = int(input())
D = [0] + list(map(int, input().split()))
L1, C1, K1 = map(int, input().split())
L2, C2, K2 = map(int, input().split())
def pair(i):
n = 0
while True:
l1 = L1 * n
left = D[i] - l1
m = 0
if left > 0:
m = left // L2
if left % L2 != 0:
m += 1
yield (n, m)
if left <= 0:
break
n += 1
INF = K2 + 1
dp = [INF]*(K1+1)
dp[0] = 0
for i in range(1, N+1):
ndp = [INF]*(K1+1)
for n, m in pair(i):
for pn, pm in enumerate(dp):
nn = pn + n
if nn > K1:
break
if pm != INF:
nm = pm + m
if nm <= K2:
ndp[nn] = min(ndp[nn], nm)
dp = ndp
ans = 10**17
for n, m in enumerate(dp):
if m != INF:
ans = min(ans, C1 * n + C2 * m)
print(ans if ans != 10**17 else -1)G - offence
x ★ 1ヶ月以上放置してたのをようやくAC。何度もNG回答提出しまくって、苦手意識強め。これはあまり見たくないなぁ。yellow #区間DP 2023-11-26
S = list(input())
K = int(input())
N = len(S)
dp = [[0]*(N+1) for _ in range(N+1)] # 残るもの、未初期化
for l in range(N):
dp[l][l] = 1
for w in range(1, N): # r-l
for l in range(N - w):
r = l + w
dp[l][r] = w + 1 # init
if S[l] == 'o':
for f in range(l+1, r+1)[::-1]:
if S[f] == 'f' and dp[l+1][f-1] == 0:
dp[l][r] = min(dp[l][r], max(0, dp[f+1][r]-K))
for i in range(l+1, r+1):
dp[l][r] = min(dp[l][r], dp[l][i-1] + dp[i][r])
print(dp[0][N-1])AtCoder Beginner Contest 326
ABCDE、5完。Fは半分全列挙だと気づいてオーシッって思って取り組んでたけど全然実装が間に合わなかった。F開始時40分残ってたのに。コンテスト直後、惜しいなどと思ってたけど、他の人見てると、同じようなこと言ってる人が結構いたので、短時間で実装する力が求められているということに過ぎないのだと思う。今回はDも実装が大変なタイプだった、っていうか最近実装が大変な問題がC、Dあたりに配置されてる傾向があるように思う。このあたりは、反省すべき点。
D - ABC Puzzle
o ★見たくないなぁと思いながら反省。40分かかったのは時間かかり過ぎなのだろう。結構ひどいコードだと思う。あまりよくない方針で書き始めて、後手後手で修正するとこうなる。N行全部作ってから各列調べても間に合うなーと思ったけど、ループをどう回そうか?となってしまった。というわけで、Nを統一的に扱って、できるだけシンプルになるようにちょっと書き直してみた。productに自分で作ったonelineというiteratorのリストを渡してみたが、おそらく中身が全部前計算されてしまうらしく、retオブジェクトは新規作成する必要があった。順番にやってくれないのかぁ。(★のところ。)あ、公式ドキュメントに書いてあった。
product() は動作する前に、入力のイテラブルを完全に読み取り、直積を生成するためにメモリ内に値を蓄えます。したがって、入力が有限の場合に限り有用です。
Before product() runs, it completely consumes the input iterables, keeping pools of values in memory to generate the products. Accordingly, it is only useful with finite inputs.
でもだいぶ見通し良くなってマシなコードになった気はする。こういう反省大事。実装力というタグ作っとく笑。 light blue #実装力 2023-10-28
from itertools import combinations, product
def oneline(a, b, c, n):
for i, j, k in combinations(range(n), 3):
ret = ['.']*n
ret[i], ret[j], ret[k] = a, b, c
yield ret
ret = ['.']*n # ★
ret[i], ret[j], ret[k] = a, c, b
yield ret
args = {'A': ['A', 'B', 'C'],
'B': ['B', 'C', 'A'],
'C': ['C', 'A', 'B']}
N = int(input())
R = list(input())
C = list(input())
ls = []
for i in range(N):
ls.append(oneline(*args[R[i]], N))
for res in product(*ls):
for j in range(N):
cs = []
for i in range(N):
if res[i][j] != '.':
cs.append(res[i][j])
if len(set(cs)) != 3:
break
if cs[0] != C[j]:
break
else:
print('Yes')
for i in range(N):
print(''.join(res[i]))
break
else:
print('No')F - Robot Rotation
o ★ Dで作った実装力タグがこの問題にもさっそく適用。半分全列挙だ!と思っていけるぞ!と取り組んでたがコンテスト終了に間に合わなかった。悔しい。短時間での実装力が求められる。最初のミスは、「半分全列挙」を文字通り半分にしようとしてしまったこと。無意識に名前に釣られてた。半分にしようとするといろいろやっかい。とくに小さい数字の時とか。よく考えたら。2^20が100万程度だから計算量が抑えられるのであって、20より大きかったら残りを分離するということで良い。その方が実装がシンプルになる。常に20とわかっているから、常に20bitシフトさせて結合すればよいわけだし。あと、関数化。上下移動と、左右移動をどちらでも扱える関数を1つ作るべき。その判断すらできないと、とんでもなく大変なことになる。半分全列挙の突き合わせはまあいいだろう。今回は上下と左右の結果をマージする処理も必要!これが大変だわ。コードが長くなるとミスも入る。bitが1なら+方向、0なら-方向として実装した。この場合、左右から上下に移るときは、bitが同じならL、異なるならR、上下から左右に移るときは、bitが同じならR、異なるならL、という法則に気づくと、短く書けた。if/elseで全部書くとどんどんコードが伸びてつらい。blue #半分全列挙 #実装力 2023-10-28
def check(ds, goal):
'''
ret >= 0: way
ret < 0: impossible
ret = None: len(ds) == 0 and possible
'''
nds = len(ds)
nf, ns = nds, 0
if nds == 0:
if goal == 0:
return None
else:
return -1
if nds > 20:
nf, ns = 20, nds - 20
fposis = [0]*(2**nf)
for bit in range(2**nf):
posi = 0
bitcopy = bit
for i in range(nf):
if bitcopy % 2 == 1:
posi += ds[i]
else:
posi -= ds[i]
bitcopy //= 2
fposis[bit] = posi
if nds <= 20:
for bit in range(2**nf):
if fposis[bit] == goal:
return bit
return -1 # not found
posi2bit = {}
for bit in range(2**ns):
posi = 0
bitcopy = bit
for i in range(nf, nds):
if bitcopy % 2 == 1:
posi += ds[i]
else:
posi -= ds[i]
bitcopy //= 2
posi2bit[posi] = bit
for bit in range(2**20):
if goal - fposis[bit] in posi2bit:
return bit + (posi2bit[goal - fposis[bit]] << 20)
return -1
N, X, Y = map(int, input().split())
DU = [] # down up
LR = [] #
for i, a in enumerate(map(int, input().split())):
if i % 2 == 0:
DU.append(a) # 0, 2, 4,
else:
LR.append(a) # 1, 3, 5
du = check(DU, Y)
if du == -1:
print('No')
else:
lr = check(LR, X)
if lr == -1:
print('No')
elif lr is None:
print('Yes')
print('L' if du == 1 else 'R')
else:
ans = []
pre = 1
for i in range(len(LR)):
cur = du % 2
ans.append('L' if cur == pre else 'R')
pre = cur
du //= 2
cur = lr % 2
ans.append('R' if cur == pre else 'L')
pre = cur
lr //= 2
if len(DU) > len(LR):
ans.append('L' if du % 2 == pre else 'R')
print('Yes')
print(''.join(ans))G - Unlock Achievement
x ★ 燃やす埋めるだと思って考えてもどうグラフを作ればいいかわからないし、今回は答えを見てもよく理解できてない。今までは一応理解できてたんだけど。この問題で混乱してしまう原因は、あるスキルについて、アチーブメントに必要なレベルを達成していても、他のスキルが達成していなければ、アチーブメントできない(=そのアチーブメントが最小カットになる)ということだと思う。が、そんなことを言ってる時点でぼくは最小カットをよくわかってないんだろうなぁと感じる。
少し考えてわかった部分もあるので、意味を書こうと思う。まず、最小カットの意味をもう一度確認しておく。残余グラフを考え、ある頂点に到達できて、その先の頂点に到達できない時、最小カットという。残余グラフの向こう側への辺。今回、レベル2からレベル3へ、レベル3からレベル4へ無限キャパの辺をつなぐが、これが意味していることは、レベル3の辺が最小カットだが、レベル2の辺が最小カットではない。というようなことが起きないことを意味している。なぜならレベル2の辺のキャパが余っていたら、このようなつなぎ方であれば、すべてのレベルが、最小カットではない状態になる。レベル3の辺がもうフルで流れていたとしても、レベル2の辺が余っていれば最小カットにはならない。このことが重要。つまり、このつなぎ方をすると、最小カットはレベル2、3、4、5と順番に増えていく。これは望み通りの挙動と言える。あるアチーブメントが、最小カットであるとはどういうことか?残余グラフが、アチーブメントまで届いており、アチーブメントのシンクへの辺は使い尽くしているという状態である。残余グラフが到達できるということは、いずれかのスキルにおいて、レベルの最小カットが、そのアチーブメントが必要なレベルに到達していないということである。確かに望み通りの挙動だ。逆にアチーブメントが最小カットではないとはどういうことか?そのアチーブメントまで残余グラフが到達できないということであり、必要なレベルの頂点まで、スキルのほうが最小カットになっているということだ。これは望み通りの挙動だ。このように、意味がわかってきたけど、同様の問題に出会ったときに思考のショートカットをできるほどの理解ではない。自力でグラフを構築できるのか?なぞである。
まだわからん、なんでこれで最小コストが求まるんだ?と疑問がわきあがってきた。最小性はどう示される?ていうか最小カットって言ってんだから最小だろうってのが正解なんだけど。つまり、カットでコストを表現するグラフを作る。最大流を流す。最小カットに流れるフローの合計と最大流のフローが一致する。最大流に最大ってついてるのもなんか、理解の妨げになってる気がするけど、求めたいのは「最小カット」。「カット=コストの合計」が最小になるのが最小カットであり、その合計は最大流のフローと一致するという性質を利用するということ。キャパが無限の辺は最小カットになりえないという性質を利用し、グラフに問題の条件を組み入れることをする。レベルは低い順にしか最小カットにならない。また、アチーブメントが最小カットでないとき、必ずそのアチーブメントに必要なスキルのレベルがすべて最小カットになっているという条件を表現している。また、いずれかのスキルが必要なレベルを達成していなければ、アチーブメントが必ず最小カットになっているという条件も組み込まれている。その状態で最大流を流す。その合計と一致するカットが最小カット。このカットはコストの中で最小である。もっと小さなカット=コストが存在するなら、最大流がそのサイズしか流れないはず。現在流れているのだから、これ以上小さなコストは存在しない。これで説明になってるかな。。。なんかグラフがどうなってるか考えまくって行き詰まってた。半日考え続けてこの結論に到達した。このグラフにおけるキャパINFを除くすべての辺はスキルアップコストと、アチーブメントロストコストを表現していて、最小カットはその中の辺で構成され、最小値なのだから、やはり最小コストだよ。よしッ。燃やす埋めるに初めて出会ったときにこういうことたぶん考えて、理解したと思うけど、しばらく経つと忘れてるんだろうなと思う。今回のようにもう一度考え直して再構築できたらちゃんと定着するんじゃないかな。orange #燃やす埋める #最小カット #最大流 2023-10-28
N, M = map(int, input().split())
C = list(map(int, input().split()))
A = list(map(int, input().split()))
L = []
for _ in range(M):
L.append(list(map(int, input().split())))
mf = MF(5*N + M + 2)
S, G = 0, 5*N + M + 1
for i in range(N):
base = 5 * i
for j in range(2, 6):
mf.add_edge(S, base + j, C[i])
mf.add_edge(base + j - 1, base + j, MF.INFFLOW)
for i, need in enumerate(L):
v = 5 * N + i + 1
for j in range(N):
mf.add_edge(5 * j + need[j], v, MF.INFFLOW)
mf.add_edge(v, G, A[i])
print(sum(A) - mf.mf(S, G))AtCoder Beginner Contest 327
ABCD、4完。青パフォ3連続からの緑パフォという悔しい結果となった。Eを、最大値のDPなのかな?と思ったが、それでいいことを証明できず、飛ばしてFへ。Fわからず、Eに戻って無証明提出したところTLE。一部事前計算するように少し変えたところ、AC。結果的には無証明でも飛ばさずにやってれば解けた可能性が高いとわかり悔しい。途中で崩れると集中力が切れて頭が働かず、その後もうまくいかないことが多い。睡眠不足?ビール飲みすぎ?など体調管理についても考えてしまう。今週は木曜まで睡眠不足。昨日は酒も飲まず9時間ぐっすりでうれしかったが。1日よく寝てもだめね。そういえば最近、平日競プロの問題考えすぎてて頭が疲れすぎてる気がするので、今日は1日別のことしてた。
D - Good Tuple Problem
o 最近見たUnionFindによる2部グラフ判定を使えた。#2部グラフ判定 #UnionFind 2023-11-04
E - Maximize Rating
o ★ コンテスト中解けず。最悪だ。その後解けた、が。Rの値の最大値でDPしており、なぜそれで通るのか証明できておらず、制限時間2秒に対して、1730msとギリギリだった。なるほど、Rの値を見ると、第1項の分母と、第2項はすべて、パフォーマンスの値は入っておらず、k(選んだコンテストの数)だけで決まる。つまり、k個選んだ場合に注目すると、第1項の分子が最大であれば良いとわかる。i番目のコンテストをk個目として選ぶ場合の分子は、(すでに選んだk-1個で作った分子)x0.9 + Piなので、(すでに選んだk-1個で作った分子)が最大の場合から遷移したときに、最大となることがわかる。これコンテスト中に気づけないとダメじゃん、と心から思う(T_T) light blue #DP 2023-11-04
N = int(input())
P = list(map(int, input().split()))
dp = [0]*(2) # iまででk個選んだときの分母最大
dp[1] = P[0]
for i in range(1, N):
ndp = [0]*(i+2)
for j in range(i+1): # i-1までj個洗濯
ndp[j] = max(ndp[j], dp[j])
ndp[j+1] = dp[j] * 0.9 + P[i]
dp = ndp
ans = -10**15
bunbo = 1
for j in range(1, N+1):
ans = max(ans, dp[j]/bunbo - 1200/(j**0.5))
bunbo = bunbo * 0.9 + 1
print(ans)F - Apples
x ★ 悔しいがわからず。1辺が200000のグリッド内に、点(T, X)が200000個ある。DxWの長方形の中に含まれる点の個数の最大値は?という問題であることがわかる。むちゃくちゃ典型っぽい見た目してるけど解けなかった。長方形の左上の点に注目するらしい。左上の点がどこにあれば、(T, X)が長方形に含まれるか?と考えると、(T-D~T, X-W~X)であることがわかるので、この範囲に+1するとする。すべての(T, X)に対してこの作業をすると、ある点を左上としたときに、いくつの(T, X)が含まれるかわかるので、その最大値を調べる問題となる。よって、遅延セグ木でTを走査しながらXの区間に+1し、最大値を調べていけば、答えがわかる。制限時間2秒で1850ms。やば。blue #遅延セグ木 #典型 2023-11-04
N, D, W = map(int, input().split())
segt = SEGT_LAZY(200001)
events = []
for _ in range(N):
t, x = map(int, input().split())
l, r = max(1, x-W+1), x+1 # [l, r)
events.append((max(1, t-D+1), l, r, 1))
events.append((t+1, l, r, -1))
events.sort(key=lambda x: x[0])
i = 0
ans = 0
while i < len(events):
t, l, r, a = events[i]
segt.range_add(l, r, a)
i += 1
while i < len(events) and events[i][0] == t:
t, l, r, a = events[i]
segt.range_add(l, r, a)
i += 1
ans = max(ans, segt.query(1, 200001))
print(ans)G - Many Good Tuple Problems
x ★ 久しぶりに赤Diffやった。N頂点k辺の単純な2部グラフを数え上げたい。DPでは?と思うけど、なんかうまくいかない。考えると行き詰まって頭が限界になって力尽きる。解説見るとかなりやっかいな方法でようやく2部グラフを数え上げている。このややこしい手順の必要性が、ちゃんと腑に落ちるかどうか?N頂点k辺の単純な2部グラフを数え上げるにはこの手順が確かに必要なのだ。M=10^9だが、N頂点k辺の単純な2部グラフの数が分かれば、あとは、k辺すべてを使い、1-Mの辺を割り当てる方法を数える問題となる。これは包除原理を使って数えることができる。k個の箱に空箱を作らないようにM個のボールを入れる方法の数は包除原理で数えられる。どれかの箱が空の場合を引く問題だ。この問題においては辺の向きもあるので、その2^M倍が答えとなる。ではN頂点k辺の単純な2部グラフはどのように数えるか?まず、頂点をグループ0と1に分け、0と1間の全辺の中からk本選ぶ方法は、簡単に求められる。これをf(n, k)とする。ここまではやってみようとするだろうが、求めたい値にならないのは明らかだ。辺でつないでいない頂点や、辺でつながっている連結成分は、グループ0と1が逆になっていても同じグラフとみなしたいが、区別されてしまっているからだ。ここで力尽きてしまうが、ここから2ステップを踏んで求めたい数え上げにたどり着く。最初に、n頂点k辺の連結な2部グラフの数g(n, k)を求める。そのためにf(n, k)から連結でないものを引いていく。連結でないものはどのように数えるかというと、除原理を使う。1つの頂点を固定し、その頂点を含むn-1頂点以下のすべての連結のグラフの数が求まっているとすると、それらはすべて異なっているので、固定した頂点と連結でない頂点に対してはfをかけることで、n頂点で連結でないものをすべて数え上げられるのだ。g(1, ?)は計算せずに求まるので、g(2, ?)以降は、DPを使って順番に計算することができる。g(n, k)は実際にはグループ0と1を逆にしたものも数えているので、g/2が連結な2部グラフの数になる。この求まった連結なグラフの数を用いて、今度は逆にグループ0と1を区別しない、非連結も含めた数h(n, k)をまたDPで求めていく。今度も1つの頂点を固定する。そしてその頂点を含むn-1個以下のすべての連結成分に対して、残りの頂点はすでに求まったhを使って計算すれば良い。今回もh(1, ?)は計算せずに求まるので、h(2, ?)以降がDPで求まることになる。red #数え上げ #DP #2部グラフ #除原理 #除原理DP 2023-11-08
import sys
mod = 998244353
N, M = map(int, input().split())
if N == 1:
print(0)
sys.exit()
if M == 1:
print(N*(N-1))
sys.exit()
halfN = N // 2
L = halfN * (halfN + N % 2) # L: max edge num
COUNT_MAX = max(N, L)
fact = [0]*(COUNT_MAX+1)
invfact = [0]*(COUNT_MAX+1)
fact[0] = 1
for i in range(1, COUNT_MAX+1):
fact[i] = fact[i-1] * i % mod
invfact[COUNT_MAX] = pow(fact[COUNT_MAX], mod-2, mod)
for i in range(COUNT_MAX-1, 0, -1):
invfact[i] = invfact[i+1] * (i+1) % mod
invfact[0] = 1
def choose(n, r):
if n < r:
return 0
return fact[n] * invfact[r] * invfact[n-r] % mod
powM = [pow(k, M, mod) for k in range(max(3, L+1))] # ★ need powM[2] at last!
Mink = [0]*(L+1)
for k in range(1, L+1): # k本の辺を1-Mを割り振ってすべて使う方法の数
s = 1
cur = 0
for i in range(k+1): # i個使わない
cur = (cur + s * choose(k, i) * powM[k - i]) % mod
s *= -1
Mink[k] = cur
f = [[0]*(L+1) for n in range(N+1)]
f[1][0] = 2
for k in range(1, L+1):
f[1][k] = 0
for n in range(2, N+1):
for k in range(L+1):
cur = 0
for i in range(n+1): # select i vertices for group0
nedge = i * (n - i)
cur = (cur + choose(n, i) * choose(nedge, k)) % mod
f[n][k] = cur
g = [[0]*(L+1) for n in range(N+1)] # connected
g[1][0] = 2
for k in range(1, L+1):
g[1][k] = 0
for n in range(2, N+1):
for k in range(L+1):
g[n][k] = f[n][k]
for i in range(1, n):
for m in range(k+1):
g[n][k] = (g[n][k] - choose(n-1, i-1) * g[i][m] * f[n-i][k-m]) % mod
inv2 = pow(2, mod-2, mod)
h = [[0]*(L+1) for n in range(N+1)] # not connected
h[1][0] = 1
for k in range(1, L+1):
h[1][k] = 0
for n in range(2, N+1):
for k in range(L+1):
h[n][k] = g[n][k] * inv2 % mod
for i in range(1, n):
for m in range(k+1):
h[n][k] = (h[n][k] + choose(n-1, i-1) * (g[i][m] * inv2) * h[n-i][k-m]) % mod
ans = 0
for k in range(L+1):
ans = (ans + h[N][k] * Mink[k]) % mod
print(ans * powM[2] % mod)AtCoder Beginner Contest 328
ABCD、4完。2連続で崩壊した。Eは全域木列挙でいけると思ったけどどうやればいいかわからなかった。最悪だ。動揺してFへ。いつものように、一度崩れると立て直せず、閃かず。E、Fを行き来するも時間が過ぎ、残り3分でFのやり方を閃いたが間に合う訳なし。しまった。E、辺の数の最大数8x7=56と勘違いして間に合わないと思いこんでた。8x7/2=28本しかないじゃん。うはー。余裕でいけたじゃん!つらすぎる。E、Fいけたじゃん(T_T) そもそも、最近寝不足で死にそうなのかもしれない。寝ようと思っても問題を見てしまって、そのたびに知らないことが出てきて、理解に時間を要し、寝れない。仕事も忙しいし。頭も回復しないし、体が壊れる。
E - Modulo MST
o 8頂点の辺の数を8x7=56と勘違いし、木の辺数である7を選ぶ56C7=231917400から、全列挙できないと勘違い。実際は28本なので余裕だった。1度崩れると立て直せないのがやばい。Fも解けず。この問題を解けなかったせいでコンテスト全体が崩壊した。クソ。 2023-11-11
F - Good Set Query
o 重み付きUnion-Findそのものらしいが、ぼくはそれを知らず、Union-Findで解いた。6問目のFに、まんまの問題が置いてあるのは糞だと思った。知ってる人が一瞬で解きまくっていたのが、しょーもない。6問目にそんな問題が配置されてていいのだろうか?ぼくのやりかたは、連結成分内の2点のクエリは、すぐに処理せず、後回しにするというもの。よく考えたら、すでに連結成分になっている状態で、整合性が取れるか?は非連結を全部つないでから、1度だけ連結成分内の距離を計算し、後で調べればいい。なかなかではないだろうか?「クエリ後回し」と名付けた。#Union-Find #クエリ後回し 2023-11-11
ans = []
N, Q = map(int, input().split())
uf = Union(N+1)
G = [[] for _ in range(N)]
later = []
for q in range(1, Q+1):
a, b, d = map(int, input().split())
a, b = a-1, b-1
if not uf.same_tree(a, b):
ans.append(q)
uf.unite(a, b)
G[a].append((b, -d))
G[b].append((a, d))
else:
later.append((q, a, b, d))
INF = 10**15
dist = [INF]*N
for v in range(N):
if dist[v] == INF:
stack = [v]
dist[v] = 0
while stack:
cur = stack.pop()
for nex, d in G[cur]:
if dist[nex] == INF:
stack.append(nex)
dist[nex] = dist[cur] + d
for q, a, b, d in later:
if dist[a] != INF and dist[b] != INF and dist[a] - dist[b] == d:
ans.append(q)
ans.sort()
print(*ans)ムカつくので、当然のごとくこっちもやっておく。Union-Findはfind_rootした瞬間にrootまでのパス上のノードが全部root直下に縮約される仕組みになっている。このとき、同時に重みもrootとからの重みに縮約してしまっている。再帰呼び出し時、親ノードが先にroot直下に移動して、rootからの重みに変更されるので、その重み+親から自分への重みを新しい重みとしてセットする。rootが親になるのだから。 #重み付きUnion-Find 2023-11-15
G - Cut and Reorder
x ★ この問題くらいのDPのイメージは、すぐに浮かびたいところだが、まだ実力ない。bitDPでAのすでにつかった数字と、最小コストを管理し、次使える区間(bitの0のところの区間)すべてに遷移するDPをやる。連続している区間を使っているのに、分離してCのコストを払う場合の遷移が含まれて気になるが、分離しない場合も必ず含まれているので、そっちのコストが小さくなり、連続しているのに分離した遷移は採用されない。このセンス大事。制限時間が厳しい問題で、ちゃんと効率化しないとTLEになってしまう。次選ぶ区間を幅1-Nで全部空いてるか調べていたら間に合わず、Aを前から1bitずつ調べて空いていたら1bitずつ区間を広げて遷移して、と最小限でやらないといけなかった。#DP 2023-11-11
N, C = map(int, input().split())
A = list(map(int, input().split()))
B = list(map(int, input().split()))
INF = 10**18
bitmax = 2**N
dp = [INF]*(bitmax)
dp[0] = -C
for bit in range(bitmax):
bc = bit.bit_count()
for a in range(N):
a_ = a
abit = 1 << a
b = bc
curdiff = 0
curbit = 0
while bit & abit == 0 and a_ < N and b < N:
curdiff += abs(A[a_] - B[b])
curbit += abit
dp[bit + curbit] = min(dp[bit + curbit], dp[bit] + curdiff + C)
a_, b = a_+1, b+1
abit <<= 1
print(dp[bitmax-1])AtCoder Beginner Contest 329
3回連続完敗。前回は勘違いからのミスなどと言っていたが、今回はE、Fどちらも普通にわからなかった。Eの解説は賢いと思ったし、Fは解説を見てもすぐに理解できなかった。自信をなくした。
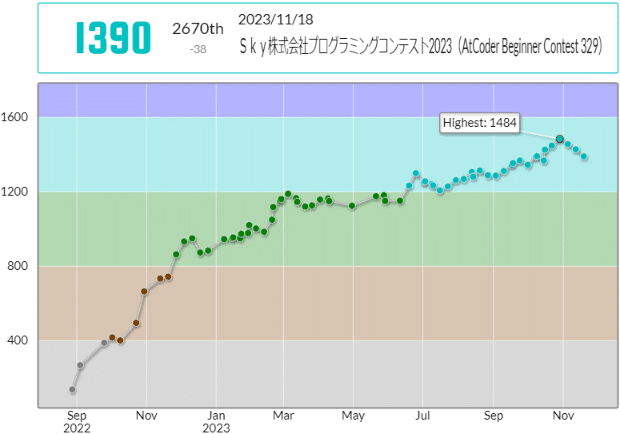
E - Stamp
x ★ M文字のところをまず見つけて、左右に貪欲に広げていくというような方針を考えたが、ややこしくて書ききれず。解説によるとキューを使うとのこと。これは賢い。キューを使えば確かにきれいにわかりやすく書ける。完敗だ。貪欲が汚くなりそうな時、キューを使えるか検討するのはありかもしれない。 #貪欲 #キュー 2023-11-19
これ賢い。これがやりたかったんだよ。上に書いた「左右に貪欲に広げていく」っていうの。確かに行って戻ればそれができる!
ABC329 E問題
— 椿ミント (@310icecrystal) November 18, 2023
未証明で投げたら通りました。
未証明なので嘘解法かもしれない。 pic.twitter.com/qAhxUCRnye
F - Colored Ball
x ★ サイズが小さい方を大きい方にマージする戦略で間に合うらしい。これが間に合うと、自分では気づけなかった。解説を見ても何を言ってるかわからず。小さい方を大きい方にマージするというのは、つまり、マージすると2倍以上のサイズになるということ。つまり、その小さい方に入っているボールはO(Log N)回のマージで済む。N個のボールをLog N回マージするので、O(N Log N)だ。setの和はO(a + b)なので、O(N)なのだ。大きい方の集合がイメージしづらく、理解に時間がかかった。しかし、大きい方はマージしない。と考えるのだ。大きい方はそれをさらに分割して半分以下になったものがマージ対象。よって、マージしていくツリーみたいなものを考えると、同じ深さでのマージ数はO(N)になる。これを自力でスッと考えられなかったのは悔しい。そんなレベルなのだ。 #2分木 #set 2023-11-19
N, Q = map(int, input().split())
box = [set() for _ in range(N)]
for i, c in enumerate(map(int, input().split())):
box[i].add(c)
for _ in range(Q):
a, b = map(int, input().split())
a, b = a-1, b-1
if len(box[a]) <= len(box[b]):
box[b] |= box[a]
box[a] = set()
else:
box[a] |= box[b]
box[b] = box[a]
box[a] = set()
print(len(box[b]))AtCoder Regular Contest 168
AB、2完。Cを1時間以上考えるも、ACできず。これはわかったか!と思ってがんばってたが、間違った考察してた。間違った考察し始めて、抜け出せないこと多い。それなんとかしたい。Cを解いた時点でAcceptedが777だった。777問って4517位なのか。みんな自分よりやたらAccepted数が多いイメージだったけど。
C - Swap Characters
x ★ コンテスト時間中にできないのつらいね。知らない知識を使うわけでもないのに、間違い考察から抜け出せず、解けずにフィニッシュ。20年以上前の高校生の頃の数学の勘は、戻ってこないな。AB、BC、CAのスワップとABCのローテーション(2回の操作でローテーションできて、方向は2通りある。)の組み合わせで最小操作で、ということまで気づいていたが、そこから誤った方向に進んでいって、組み合わせをただ数え上げればよいと勘違いしてしまった。よく考えたら、ABC->BCA、とABC->CABという2つのローテーション(4手)は、スワップ3手で同じことができる。よって逆方向のローテーションは最小手数ではないので、数え上げに失敗する。最小手数において、ローテーションは同じ方向のものしかない!あーああー、悔しい。ちゃんと整理して気づけよー。まあそれだけでなく、AからいくつBに変わって、いくつCに変わってという組み合わせをカウントすることにも気づいてなくて、変な計算しちゃってたので、WAは必然だった。スッキリ、曇のない考察ができるようにしていかねば。yellow #数え上げ 2023-11-20
N, K = map(int, input().split())
mod = 998244353
COUNT_MAX = N
fact = [0]*(COUNT_MAX+1)
invfact = [0]*(COUNT_MAX+1)
fact[0] = 1
for i in range(1, COUNT_MAX+1):
fact[i] = fact[i-1] * i % mod
invfact[COUNT_MAX] = pow(fact[COUNT_MAX], mod-2, mod)
for i in range(COUNT_MAX-1, 0, -1):
invfact[i] = invfact[i+1] * (i+1) % mod
invfact[0] = 1
def choose(n, r):
return fact[n] * invfact[r] * invfact[n-r] % mod
S = list(input())
ORDA = ord('A')
count = [0]*3
for c in S:
count[ord(c) - ORDA] += 1
a, b, c = count
ans = 0
for ab in range(min(K+1, a+1, b+1)):
a1, b1, c1, k1 = a-ab, b-ab, c, K-ab
for bc in range(min(k1+1, b1+1, c1+1)):
a2, b2, c2, k2 = a1, b1-bc, c1-bc, k1-bc
for ca in range(min(k2+1, c2+1, a2+1)):
a3, b3, c3, k3 = a2-ca, b2, c2-ca, k2-ca
for abc in range(min(k3//2+1, a3+1, b3+1, c3+1)):
if abc == 0:
ans = (ans
+ choose(a, ab) * choose(a-ab, ca)
* choose(b, ab) * choose(b-ab, bc)
* choose(c, ca) * choose(c-ca, bc)) % mod
else:
ans = (ans
+ choose(a, ab) * choose(a-ab, ca+abc)
* choose(b, bc) * choose(b-bc, ab+abc)
* choose(c, ca) * choose(c-ca, bc+abc)
+ choose(a, ab+abc) * choose(a-ab-abc, ca)
* choose(b, bc+abc) * choose(b-bc-abc, ab)
* choose(c, ca+abc) * choose(c-ca-abc, bc)) % mod
print(ans)D - Maximize Update
x ★ (L, R)という区間のリストが与えられる。l <= L <= m <= R <= rなる、(L, R)は、いくつあるか?これを2次元累積和でやるのは自力で見えない。感動した。2次元累積和なんてグリッドでしかやったことないし。l, rで2次元累積和すると、たしかに、Lがある範囲にあって、Rがある範囲にあるものをO(1)で数えられる。上の条件はl <= L <= mかつ、m <= R <= rということなので、まさに2次元累積和で扱うような条件なのだった。すげー。それを短時間で計算できないとこの区間DPにも気づけないか。。そのマスを最後に塗ると考えると、(l, r)区間で1マス抜いて、両側は最大操作数が求まっているとし、抜いた1マスをまたぐものがあれば1加えて遷移というDPができる。orange #2次元累積和 #DP 2023-11-21
N, M = map(int, input().split())
LR = [[0]*(N+1) for _ in range(N+1)]
LRac = [[0]*(N+1) for _ in range(N+1)]
for _ in range(M):
l, r = map(int, input().split())
LR[l][r] = 1
for l in range(1, N+1):
for r in range(1, N+1):
LRac[l][r] += LRac[l][r-1] + LR[l][r]
for r in range(1, N+1):
for l in range(2, N+1):
LRac[l][r] += LRac[l-1][r]
dp = [[0]*(N+2) for _ in range(N+2)]
for i in range(1, N+1):
dp[i][i] = LR[i][i]
for w in range(1, N):
for l in range(1, N-w+1):
r = l + w
for m in range(l, r+1):
can = 1 if LRac[m][r] - LRac[l-1][r] - LRac[m][m-1] + LRac[l-1][m-1] > 0 else 0
dp[l][r] = max(dp[l][r], dp[l][m-1] + dp[m+1][r] + can)
print(dp[1][N])AtCoder Beginner Contest 330
F、2分探索でやろうとしたが実装激重で50分あったのに間に合わず。貪欲でいけるらしい。貪欲のほうがシンプル。しかし結構罠もあるので、時間内は厳しいかもという印象。Eまでが緑Diff以下らしく、速解きが多すぎてボロ負け。つらい。なんでみんなそんな速いの?D茶DIff、E緑Diffって厳しすぎる。なんか先が見えない。
B - Minimize Abs 1
o 問題文確かにややこしいよね。冷静になると大丈夫だけど。Twitterでわからないと言ってる人を観測することによって、安心感を得られるな。ぼくは読解に自信がない方なので。逆にものすごいスピードで解いてる人に対しては、すぐ理解できていいなぁ、と思う。AI使ってないよね。
D - Counting Ls
o これそんなに簡単?茶Diffって。茶で60%解けるとは。わからんわ。brown 2023-11-25
F - Minimize Bounding Square
x ★ 思いついた2分探索が実装重すぎて失敗。解説見たら貪欲と書いてあった。この問題を考察していると、最初貪欲のアルゴリズムが思いつくと思うけど、N=200000もK=4x10^14も解決できず、あきらめて2分探索で行こうとなったんだけど、貪欲か。x、yで幅が広い方を狭めるのが優先。で、数が少ない方を動かす方がコストが小さい。x、yの幅が同じところで一旦止めなければならない。(これ忘れて最初WA取れなかった。)x、yの幅が同じになったら、x方向、y方向両方の数が少ない方を同時に動かす必要があるので。貪欲に持ち込むのが結構ややこしい。完敗。blue #貪欲 2023-11-25
AtCoder Heuristic Contest 027
AHC初参加。333位。どうしても2023年のうちにAHCを経験したく。おもしろさを感じられた、が、しんどい。コンテスト自体もだけど復習も大変。解説動画の内容もレベルが高かった。ちゃんと学習しようと思うと、延長戦にとりくむべきだろう。
AtCoder Beginner Contest 331
う、書き忘れてた。12月20日なう。次回ギリギリで5完。このときは横ばいだった。思い出した。Dが大変だったんだ。D、50分かかってた。これ、書き忘れてたの、ちょうどAHC027に参加したからだな。
D - Tile Pattern
o コンテスト中に解けてよかったが、50分かかった。ほぼ想定解法だった。NxNが何個入るか?あとははみ出した分を累積和でなんとかした。light blue 2023-12-02
E - Set Meal
o 2分探索でやったが、解説に2分探索は出てこず。解説の「単純な解法」っていう別解がかなり賢い。すべての主菜に対して、一番安くて可能な組み合わせを1つ見つけていく。確かに計算量はスキップした回数だけなので、NGの組み合わせの数にしかならない。本当に単純で賢い解法だわ。green 2023-12-02
import heapq
N, M, L = map(int, input().split())
A = []
for i, a in enumerate(map(int, input().split())):
A.append((a, i+1))
B = []
for i, b in enumerate(map(int, input().split())):
B.append((b, i+1))
B.sort(key=lambda x: -x[0])
NG = set()
for _ in range(L):
c, d = map(int, input().split())
NG.add((c, d))
a2b = [0]*N
pq = []
for i in range(N):
heapq.heappush(pq, (-A[i][0] - B[0][0], i))
while pq:
price, ia = heapq.heappop(pq)
ib = a2b[ia]
price = -price
if (A[ia][1], B[ib][1]) not in NG:
print(price)
break
if ib < M-1:
ib += 1
heapq.heappush(pq, (-A[ia][0] - B[ib][0], ia))
a2b[ia] = ib自分はこうやった。値段を決め打ったときにそれより高いものが全部NGになるかどうか?を調べながら2分探索。なので「それより高い」を調べるのも2分探索なので2分探索の中で2分探索。
import bisect
N, M, L = map(int, input().split())
A = []
for i, a in enumerate(map(int, input().split())):
A.append((a, i+1))
A.sort(key=lambda x: x[0])
Ap = [a for a, i in A]
Aid = [i for a, i in A]
B = []
for i, b in enumerate(map(int, input().split())):
B.append((b, i+1))
B.sort(key=lambda x: x[0])
Bp = [b for b, i in B]
Bid = [i for b, i in B]
NG = set()
for _ in range(L):
c, d = map(int, input().split())
NG.add((c, d))
l, r = 0, 3*10**9
while l+1 < r:
m = (l+r) // 2
ng = True
for i in range(N):
left = m - Ap[i]
ia = Aid[i]
bmin = bisect.bisect_left(Bp, left)
for j in range(bmin, M):
if (ia, Bid[j]) not in NG:
ng = False
break
if not ng:
break
if not ng:
l = m
else:
r = m
print(l)F - Palindrome Query
x ★ ローリングハッシュをセグ木に乗せると、更新に対応できる。その発想ない。ローリングハッシュは1文字目から順に1、B、B^2、B^3、…をかけて足したものなので、区間和のセグ木で計算できるからだ。回文判定なので逆からのローリングハッシュも作っておく。おもしろい。blue #ローリングハッシュ #セグ木 2023-12-02
B = 100000007
H = 2**61 - 1
N, Q = map(int, input().split())
bs = [1]
bsi = [1]
invB = pow(B, -1, H)
for i in range(1, N):
bs.append(bs[-1] * B % H)
bsi.append(bsi[-1] * invB % H)
bs_rev = list(reversed(bs))
bsi_rev = list(reversed(bsi))
S = [ord(c) for c in input()]
segt = SEGT(N)
segt_rev = SEGT(N)
for i, c in enumerate(S):
segt.set(i, c * bs[i] % H)
segt_rev.set(i, c * bs_rev[i] % H)
ans = []
for _ in range(Q):
q, a, b = input().split()
if q[0] == '1':
x, c = int(a)-1, ord(b)
segt.set(x, c * bs[x] % H)
segt_rev.set(x, c * bs_rev[x] % H)
else:
l, r = int(a)-1, int(b)-1
m1 = m2 = l
if (r-l) % 2 == 0:
m1 = m2 = (l+r) // 2
else:
m1 = (l+r) // 2
m2 = m1 + 1
if segt.query(l, m1+1) * bsi[l] % H == segt_rev.query(m2, r+1) * bsi_rev[r] % H:
ans.append('Yes')
else:
ans.append('No')
print(*ans, sep='\n')AtCoder Regular Contest 169
AB、2完で過去ベスト6のパフォーマンスとまずまずの結果。Cは閃いたが、バグっていて提出できなかった。最後かなり焦った。しかしバグを修正してもTLEとなり解決に時間を要したので、もうちょっと時間があればという話ではなかった。そういえば先週からAHC027なるヒューリスティックコンテストに初参加し、アルゴ休眠中でのコンテストだった。
A - Please Sign
o 根から同じ深さのものが同じ重みで影響するので、深い順に同じ深さのものの和を取って調べる。おもしろいなぁ。green 2023-12-09
B - Subsegments with Small Sums
o ARCはおもしろいなぁ。ちゃんと解けてよかった。Lを固定した時、和がS以下の部分列の最小個数は、前から貪欲にS以下最大のものを作っていった時の数なので、しゃくとりでまずすべてのLについて、右端を確定する。そのLに対して、全Rについて加えると?と考えると、まあこのようになる。light blue #しゃくとり法 2023-12-09
N, S = map(int, input().split())
A = list(map(int, input().split())) + [S+1] # stopper N
nex = [N]*N
r = 0
cur = A[0]
for l in range(N):
while cur <= S:
r += 1
cur += A[r]
# cur > S
nex[l] = r
cur -= A[l]
ans = [0]*N
for l in range(N)[::-1]:
if nex[l] == N:
ans[l] = N - l
else:
ans[l] = ans[nex[l]] + N - l
print(sum(ans))C - Not So Consecutive
o 一応終了後に自力でいけた。右端にnがn個までいけるので、その場合の数をdequeで記憶してはみ出したものを消して、前に追加していけばいいのでは?と思ったけど、TLEがとれなかった。よく考えたら消さなくてもn+1番目を引くだけで、計算できるので、stackでよかったと気付き、stackに変えてAC。しかし遅い。Pythonの苦しみ。速い人もいる。何か改善点あるのかも。yellow #DP 2023-12-09
import sys
from itertools import groupby
mod = 998244353
N = int(input())
A = list(map(int, input().split()))
for k, g in groupby(A):
if k > 0 and len(list(g)) > k:
print(0)
sys.exit()
dp = [[] for _ in range(N+1)] # n, n-1, ..., 3, 2, 1
sums = [0]*(N+1)
sumall = 0
# init
a = A[0]
if a == -1:
sumall = N
for n in range(1, N+1):
sums[n] = 1
dp[n].append(1)
else:
sumall = 1
sums[a] = 1
dp[a].append(1)
for i in range(1, N):
a = A[i]
if a == -1:
for n in range(1, N+1):
one = (sumall - sums[n]) % mod
dp[n].append(one)
sums[n] = (sums[n] + one - (dp[n][-n-1] if len(dp[n]) >= n+1 else 0)) % mod
sumall = sum(sums) % mod
else:
for n in range(1, N+1):
if a == n:
one = (sumall - sums[a]) % mod
dp[a].append(one)
sums[a] = (sums[a] + one - (dp[a][-a-1] if len(dp[a]) >= a+1 else 0 )) % mod
else:
dp[n] = []
sums[n] = 0
sumall = sums[a]
print(sumall)AtCoder Beginner Contest 332
ABCD、4完。EはbitDPやっててTLEx11。なんとかならないか書き直してるうちに終了。つら。はぁ。なんだかなぁ。Eの解説見るとPython殺しだったぽい。コンテスト中にPythonで20人ちょっとしかACしてない。こういうのがつらすぎる。やりきれない思いで休日を終え、つらい月曜日を迎えることになるんだ。ちなみにDPのINFをfloatにしておくとTLE解消した。まだ知らないテクが出てきた。勉強になったけどつらい。それはそうと、E500人しか解いてなかった。みんなWA出してたし。Fにいって解いてる人多数。Fは600人解いてた。ぼくはE解けてんだよ。チキショー。年内
E - Lucky bag
x ★ イライラ。これ解いたら昨日のARCに続いてコンスタントに伸びてたのになぁ。DPの保持する値がfloatなら、INFもfloatにすること。INFがintだと比較で余計に時間がかかってしまう。 #bitDP 2023-12-10
INF = float(10**20)
N, D = map(int, input().split())
i2b = [1]
b2i = {1: 0}
for i in range(1, N):
nex = i2b[-1] * 2
i2b.append(nex)
b2i[nex] = i
W = list(map(int, input().split()))
avg = sum(W) / D
wsum = [0]*(2**N)
for bit in range(1, 2**N):
if bit.bit_count() == 1:
wsum[bit] = W[b2i[bit]]
else:
small = bit & -bit
wsum[bit] = wsum[bit-small] + wsum[small]
val = [(wsum[bit] - avg)**2 for bit in range(2**N)] # 寄与
dp = [[INF]*(2**N) for _ in range(D+1)]
for bit in range(1, 2**N):
maxd = bit.bit_count()
if maxd == 1:
dp[1][bit] = val[bit]
continue
small = bit & -bit # smallを含む袋ごとに調べる
for d in range(1, min(D, maxd)):
if dp[d][bit-small] != INF:
dp[d+1][bit] = min(dp[d+1][bit], dp[d][bit-small] + val[small])
bitleft = bit - small
s = bitleft
while s:
# small is in s
if bitleft == s:
dp[1][bit] = val[bit] # 1袋のときは確定
else:
ss = s + small
for d in range(1, min(D, maxd)):
if dp[d][bit-ss] != INF:
dp[d+1][bit] = min(dp[d+1][bit], dp[d][bit-ss] + val[ss])
s = (s-1) & bitleft
ans = INF
a = 2**N - 1
for d in range(1, D+1):
ans = min(ans, dp[d][a] + (D-d)*val[0])
print(ans / D)F - Random Update Query
x ★自分の抽象化されてないPythonの関数ベタ書き遅延セグ木でやってたら全く解ける気がしなかったので、抽象化され洗練されたACLのlazy_segtreeを使うことに決めた。理解するのは大変だったけど、このわかりやすい説明を読んで、適当に書いたら動いた。抽象化することで思考も効率化されて解決へ向かうとは。文法とかちゃんと見直してC++第一歩として大切にしたいけど。何がややこしいって、この問題、セグ木の末端の値しか必要ないよね。なので、opが実質不要。そのせいでぼくの場当たり的に修正してたPythonでは思考が行き詰まってしまった。笑。opはsizeだけとりあえず計算するようにして、mappingでsizeを末端フラグにして末端だけちゃんと計算するようにしておいた。使い方が変だけどこういうもんだよね。というわけで、過去に解いたいろいろな遅延セグ木の問題をやりながらC++の勉強をし、FFTやSA-ISもACLを使いたいし、lower_bound的なのはPythonでできないのでやりたいし、徐々にC++を短時間で書けるようにしていこう!blue #遅延セグ木 #ACL 2023-12-21
// C++
using namespace std;
using namespace atcoder;
using mint = modint998244353;
struct S { mint val; int size = 0; };
struct F { mint a; mint b; };
S op(S a, S b) {
return { 0, a.size + b.size };
}
S e() {
return { 0, 0 };
}
S mapping(F f, S x) {
if (x.size == 1) {
return { f.a * x.val + f.b, 1 };
}
else {
return { 0, x.size };
}
}
F composition(F f, F g) {
auto [c, d] = f;
auto [a, b] = g;
return { c * a, c * b + d };
}
F id() {
return { 1, 0 };
}
int main() {
int N, M;
cin >> N >> M;
vector<S> A(N);
for (int i = 0; i < N; i++) {
int a;
cin >> a;
A.at(i) = { mint(a), 1 };
}
lazy_segtree<S, op, e, F, mapping, composition, id> seg(A);
for (int i = 0; i < M; i++) {
int L, R, X;
cin >> L >> R >> X;
mint a = R - L + 1;
seg.apply(L - 1, R, { (a - 1) / a, X / a });
}
for (int i = 0; i < N; i++) {
cout << seg.get(i).val.val() << " ";
}
cout << endl;
}AtCoder Beginner Contest 333
微妙な結果に終わり、年内入青はほぼ無理。笑。FがACに近い考察できてて逃したのがくやしい。昨日の忘年会で飲みすぎた影響は否めない。なんかあとちょっとのところで、高パフォーマンスRating急上昇のチャンスを逃してるのは、本当に体調管理とかも関係してくるといつも思う。
C - Repunit Trio
o 解説賢いなぁ。全桁の和が3になる4進数を小さい順に列挙するという、どれとも違う解き方してた。笑。こんなの普通にやるのは、おもしろいとは思うけど。2023-12-16
import sys
N = int(input())
count = 0
for n in range(10000000):
d = 0
ncopy = n
while n:
if n % 4 != 0:
d += n % 4
if d > 3:
break
n //= 4
if d == 3:
count += 1
if count == N:
ans = 0
x = 1
while ncopy:
if ncopy % 4 != 0:
a = ncopy % 4
ans += int('1'*x) * a
ncopy //= 4
x += 1
print(ans)
sys.exit()★解説より。制約最大の333の結果が112222222233であることが、入力例3からわかる。よって、12桁までのrepunitだけ考えれば良い。簡単に全列挙できる。なるほど~。別解多数。こういう考え方をスッとしたい。
N = int(input())
repunits = [int('1'*n) for n in range(1, 13)]
cand = []
for i in range(12):
a = repunits[i]
for j in range(i, 12):
b = repunits[j]
for k in range(j, 12):
cand.append(a+b+repunits[k])
cand.sort()
print(cand[N-1])F - Bomb Game 2
o ほとんど解けていてやりきれなかった。悔しすぎる。解けてない人結構いただけに。解説とは違うやりかただけど、連立方程式に帰着してた。最初の1人が1/2の確率でいなくなる、1/2の確率で後ろに回る。っていうのですべての人の確率の遷移を考えると連立方程式になる。最初の人だけ1/2で0、1/2で最後尾という式を書いてなくて、代わりにすべての人の残る確率の和が1という連立方程式を書いていて、これがアホすぎた。同じなんだけど、計算力下がりすぎてて手元で全然正しく解けず、ACに結び付けられなかった。先頭の人を連立方程式に組み込むだけで、きれいな対称性を持った連立方程式になり、このような単純なコードで連立方程式を解いて、1人の確率がわかると、隣の人の確率も全部わかるという状況だった。悔しい!!! #確率 #DP #連立方程式 #対称性 2023-12-16
mod = 998244353
N = int(input())
dp = [[0]*(N+1) for _ in range(N+1)]
dp[1][1] = 1
inv2 = pow(2, -1, mod)
for n in range(2, N+1):
k = [0, inv2]
for i in range(2, n+1):
k[0] = (dp[n-1][i-1] + k[0]) * inv2 % mod
k[1] = k[1] * inv2 % mod
dp[n][n] = k[0] * pow(1-k[1], -1, mod) % mod
dp[n][1] = dp[n][n] * inv2 % mod
for i in range(2, n):
dp[n][i] = (dp[n-1][i-1] + dp[n][i-1]) * inv2 % mod
print(*dp[N][1:N+1])G - Nearest Fraction
x ★橙Diffなのに、Pythonライブラリで一瞬と話題になってた。想定解放を理解しておくべきだが。#limit_denominator 2023-12-16
from fractions import Fraction
import decimal
r = input()
fr = Fraction(r)
N = int(input())
ans = fr.limit_denominator(N)
if ans != fr:
fr_ = fr - Fraction('0.00000000000000000001')
ans_ = fr_.limit_denominator(N)
if abs(fr - ans_) == abs(fr - ans):
ans = ans_
print(ans.numerator, ans.denominator)AtCoder Grand Contest 065
Aをペナルティ入れて1時間で解いたのが割と速かったっぽくて、過去最高パフォーマンス1969(しかし初黄パフォならず)、かろうじてHighest更新してRating 1493となった。
A - Shuffle and mod K
o (Ai+1−Ai) modKが最も大きくなるのは、Ai+1がAiの次に小さい時だろうということで、順番に次に小さいのを取っていけば良いと考えた。1周して、一番小さい数を最後に引く。そのままやるとWAx2だったので、そこから30分考えてたら、同じ数字が複数ある場合、そこから調べ始めないと最適にならない場合があると気づき、同じ数字が最もかぶっているところを先頭にしてから処理してAC。合ってんのか? 2023-12-17
from collections import defaultdict, deque
N, K = map(int, input().split())
A = defaultdict(int)
for a in map(int, input().split()):
A[a] += 1
q = deque([])
nmax = 0
amax = -1
for a, n in sorted(A.items(), key=lambda x: x[0]):
if n > nmax:
amax = a
nmax = n
q.append((a, n))
while q[-1][0] != amax:
a, n = q.pop()
q.appendleft((a, n))
line = []
while q:
a, n = q.pop()
line.append(a)
n -= 1
if n > 0:
q.appendleft((a, n))
line.append(line[0])
ans = 0
dmin = 10**10
for i in range(len(line)-1):
d = (line[i+1] - line[i]) % K
dmin = min(dmin, d)
ans += d
print(ans - dmin)B - Erase and Insert
x ★今まででトップレベルに難しいかも。コンテスト時間中、これでいけるか?という方針を思いついてギリギリまで実装してサンプルテストケース合わず力尽きたけど、後で嘘方針であることがわかった。操作各回独立に、全パターンからの推移を計算すればよいのでは?と思ってたけど、別の操作で同じ列になることが、余裕で存在した。それすら気づけないのは情けない限り。解説があたおか過ぎた。後ろから(Pから)操作していって、昇順のQにすると数え上げがかぶらないようにできるっぽい。うしろからの操作で、まだ操作していない数字のどの間に動かす(戻す)か?で遷移していく。数字が大きい順に動かすので、最終的に昇順にするには、すでに数字がはさまっている一番左の間か、それよりも左の間にしか挿入できない。よって、DPは、一番左の間の位置ごとに、数を保持していく。処理的には、次動かす数字の前後をマージして、それより後ろのものは、前に1つスライドさせる。右端から0埋め。からの、累積和。なぜ累積和かというと、次挿入できる位置は、先程の考察の通り、それより左側なので。どうやって気づくの?とは思うけどうしろからってのは割とありがちなトリックか。前からでもいい?とかもう考えるエネルギー残ってないんですが。笑。しんどかった。考えるのしんどいけど、サクサクのシンプルな処理になる。245ms。 #DP #数え上げ 2023-12-19
mod = 10**9 + 7
N = int(input())
P = list(map(int, input().split()))
Psort = []
for i, p in enumerate(P):
Psort.append((i, p))
Psort.sort(key=lambda x: x[1])
segt = SEGT(N)
smallleft = [0]*N
for i, p in Psort:
segt.set(i, 1)
smallleft[i] = segt.query(0, i)
dp = [0]*N # j: 0でない最初のid
for j in range(N):
dp[j] = 1
for i in range(2, N+1):
ip = smallleft[Psort[-i][0]]
dp[ip] = (dp[ip] + dp[ip+1]) % mod
for j in range(ip+1, N-1):
dp[j] = dp[j+1]
dp[N-1] = 0
for j in range(N-1)[::-1]:
dp[j] = (dp[j] + dp[j+1]) % mod
print(dp[0])AtCoder Heuristic Contest 029
2度目のAHC。1度出てしまうと、2度目も勢いで参加してしまった。404位と順位を下げた。この問題もいろいろな取り組み方がありそうで、ちゃんと復習して身につけたい。
AtCoder Beginner Contest 334
金曜は仕事を休んだし、今日も朝から38.5度の熱。日中寝ていて37度台までは下がったものの、ぼーっとしているし頭痛も酷い中、さすがにRated参加するかどうか迷った。が、なんといっても年内最後のコンテストということでRated参加した。結果は冷えたけど大失敗せず。これなら年内最後であることを考えると出てよかったと思える。まあ無茶だけど。
B - Christmas Trees
o Bにしてはかなり難しい気がする。熱のせいなのか判断できずモヤモヤしたが、冷静に10分でAC。基準となるAはMの倍数の距離動かしても結果に影響しないので、- kMして十分左に移動してしまう。LもRもAの右側になれば、L-1-A、R-AをMで割った値から簡単に求められる。区間が[L,R]なので、引く方はL-1を使う。 2023-12-23
A, M, L, R = map(int, input().split())
k = 10**19 // M
A -= k * M
L -= A
R -= A
r = R // M
l = (L-1) // M
print(r - l)C - Socks 2
o ちょっと絵を描いてみると、なくしていないペアはそのまま使えばいいと気付ける。よってなくした片方同士をペアリングしていくが、1つ飛ばしもないことは、これも絵を描けばわかる。よって、なくしたのが奇数枚のとき、どれをスキップするか?最初しょうもないミスをしてWA、飛ばしてEまで解いてから戻ってきてAC。危ない。 2023-12-23
F - Christmas Present 2
x ★ DPだが難しい。また番号順に配るという問題の条件を読み飛ばしていたのは置いといても、どうやってDPに持ち込むか?1からN-1のうちi番目に家に帰る。ただし帰るiの隣同士の差は最大でK。その場合、どこで帰るのが最も距離が短いか?という問題に帰着する。このDP結構難しい。i番目から家に帰るときの最小値でDPする。それがわかると、i > Kであれば、直前には、i-K、i-K+1、、、i-1のどこかで家に帰っている必要があり、その最小値にiで帰る場合のコストを加えたものの最小値が求めたい値となる。Nで帰ることは確定しているので、DPをN-1まで求めたら、N-K以降の最小値から答えが求まる。スライド最小値を使う。blue #DP #スライド最小値 2023-12-23
import sys
from collections import deque
INF = 10**16
def dist(a, b):
return ((a[0]-b[0])**2 + (a[1]-b[1])**2)**0.5
N, K = map(int, input().split())
S = tuple(map(float, input().split()))
XY = [tuple(map(float, input().split())) for _ in range(N)]
D = [0]*(N-1) # 家に帰ったときの増分
for i in range(N-1):
D[i] = dist(XY[i], S) + dist(S, XY[i+1]) - dist(XY[i], XY[i+1])
dp = [INF]*(N-1) # i番目から家に帰るときの最小
q = deque([])
alllen = dist(S, XY[0]) + dist(S, XY[-1])
if N == 1:
print(alllen)
sys.exit()
for i in range(N-1):
alllen += dist(XY[i], XY[i+1])
if i < K:
val = dp[i] = D[i]
while q and q[-1][1] > val:
q.pop()
q.append((i, val))
else:
if q[0][0] == i - K - 1:
q.popleft()
val = dp[i] = q[0][1] + D[i]
while q and q[-1][1] > val:
q.pop()
q.append((i, val))
if q and q[0][0] == N - 2 - K:
q.popleft()
print('{:.8f}'.format(alllen + (q[0][1] if q else 0)))G - Christmas Color Grid 2
x ★ これは、難しい。lowlinkという新しい概念が出てきた。そして内容を理解して実装してたらDFSがまたおかしいぞとなった。ABC251 Fの再来。無向グラフからDFS木を作る処理順をミスってる話。はじめから木であればDFSも何もないんだけど、無向グラフからDFSで木を抜き出すという場合、本当に進めなくなるまで行けるだけ行かないと、DFSではない。次の探索先として子供をスタックに積むが、それは確定ではない。なぜなら、兄を行けるだけ進めた結果、弟に到達すればそのルートが優先されるから。つまり、スタックから取り出したときには「すでに別ルートから通っているので捨てる」という処理が必要ということ。これを実装するのがちょっとやっかいに感じる。木を作るので、それはPというリストに、各ノードの親情報として保持することにしよう。まだ行きがけ順(order)が確定していないものをスタックに積み、このとき、Pを更新する。スタックは、最後に積んだものを取り出して探索を進めるので、あとで更新したPの情報が優先されることを利用して実装しているが、、、なんか危ういよな。ACしたけど。というわけで、まず一旦PにDFS木の情報と行きがけorderの情報を作っておく。次に、今度はその木に対してDFSをして、lowlinkを作成する。すでにDFS木があるので、子要素をスタックに積んでいけば良い。lowlinkはデフォルト値は、orderである。行きがけに、自分自身から木の外に辺がある場合は、その最も小さいorderで更新する。DFS木の、木以外の辺は必ず先祖か子孫への辺であることが保証される。別の枝への辺が存在するのであれば、かならず優先的に探索するので、そもそも別の枝にならないからである。そして帰りがけには、子どもたちのlowlinkの値で更新する。これでlowlinkが確定する。ある頂点を削除したときに、連結性が崩れるとき、その頂点を関節点と呼ぶ。関節点の子要素の条件は「子要素のlowlinkが、その頂点のorder以上」であることである。確かにそれはそう。よって頂点削除によって連結成分の数がどのように変化するかというと、上記条件を満たす子要素の数+1である。連結性が崩れない子要素は、先祖とつながったままになって1つの連結成分となるので+1。しかし削除する頂点がDFS木の根であった場合は、根の親はいないので、分離しない連結成分というものは存在しないため、+1は不要。ていうか根は、すべての子要素が上記条件を満たすはずだが。ちなみに今回出てきていないが、辺を削除したときに連結成分が2つに分かれる「橋」の条件は、その辺の子要素側のorderとlowlinkが等しいことである。yellow #lowlink #関節点 #DFS #DFS木 2023-12-29
mod = 998244353
H, W = map(int, input().split())
HW = H*W
S = [] # Green or not
for _ in range(H):
S.extend([c == '#' for c in input()])
G = [[] for _ in range(HW)]
count_green = 0
for i in range(H):
for j in range(W):
v = i * W + j
if S[v]:
count_green += 1
for dh, dw in [(-1, 0), (0, -1), (1, 0), (0, 1)]:
if 0 <= i+dh < H and 0 <= j+dw < W:
u = (i+dh) * W + (j+dw)
if S[u]:
G[v].append(u)
P = [-2]*HW # 親がわかればツリーが確定
order = [-1]*HW
count = 0 # 連結成分
for v in range(HW):
if not S[v] or order[v] != -1:
continue
count += 1
ocur = 0
stack = [v]
while stack:
cur = stack.pop()
if order[cur] != -1:
continue
if ocur == 0:
P[cur] = -1
order[cur] = ocur
ocur += 1
for nex in G[cur]:
if order[nex] == -1:
P[nex] = cur
stack.append(nex)
lowlink = [-1]*HW
for v in range(HW):
if order[v] != 0:
continue
# order[v] == 0 means its the root
stack = [~v, v]
while stack:
cur = stack.pop()
if cur >= 0:
lowlink[cur] = order[cur]
for nex in G[cur]:
if P[nex] == cur:
stack.extend([~nex, nex])
elif nex != P[cur]:
lowlink[cur] = min(lowlink[cur], order[nex])
else:
cur = ~cur
for nex in G[cur]:
if P[nex] == cur:
lowlink[cur] = min(lowlink[cur], lowlink[nex])
ans = 0
for cur in range(HW):
if not S[cur]:
continue # 赤はスキップ
inc = 0 # 連結成分の増分
for nex in G[cur]:
if P[nex] == cur:
if lowlink[nex] >= order[cur]:
inc += 1 # 分離される数
if order[cur] == 0: # 根は親がいないので
inc -= 1
ans = (ans + count + inc) % mod
print(ans * pow(count_green, -1, mod) % mod)ABC過去問
ABC269 F - Numbered Checker
o 面倒だと思い、やらないことにしていたが、ABC245以降のGを昨日全部埋めたら、ここだけ抜けているのが気になってしまい、やることにした。しかし、以前は面倒なだけだと考えていたけど、今となってはこの問題からも得るものが多い。こういう、面倒だなぁ、と思うような問題をささっと解くことが求められることが多いと、コンテスト参加を重ねてすでによく知っているので。実際面倒に見えるものを短時間で整理し、できるだけシンプルな実装に落とし込んで、解決するというのは、まさに強プロで(競プロ以外でも)必要な能力といえる。面倒だからといって嫌がっている場合ではないのだ。この問題のぼくの考え方、(1,1)から(x,y)までの範囲を計算する関数を用意して包除原理でやる、右端が奇数か偶数かでまずめんどくせーとなるけど、そこはそれくらい分岐しちゃえ、行方向も奇数偶数、めんどくさがらず分岐しちゃえ。1行の合計を計算するときに、等差数列の和を使う。で、行方向の和はどう計算するんだ?と考えると、偶奇が同じ行は各数字が2M増加するので、行全体が等差数列になるとわかる。偶数行目も2行目さえ計算してしまえば等差数列になる。たしかになんかイライラしてしまうが、ここまで整理してちゃんと書き始めると意外と大したことないよと。blue #面倒 #等差数列の和 2023-09-25
mod = 998244353
N, M = map(int, input().split())
def f(n, m):
global M
if n == 0 or m == 0:
return 0
ce = m // 2
co = ce + (1 if m % 2 == 1 else 0)
re = n // 2
ro = re + (1 if n % 2 == 1 else 0)
r1 = (1 + m) * m // 2 - (1 + ce) * ce
diffo = co * M
osum = (r1 + (ro - 1) * diffo) * ro
r2 = M * m + (1 + ce) * ce - diffo
diffe = ce * M
esum = (r2 + (re - 1) * diffe) * re
return (osum + esum) % mod
Q = int(input())
ans = []
for _ in range(Q):
a, b, c, d = map(int, input().split())
ans.append((f(b,d) - f(b,c-1) - f(a-1,d) + f(a-1,c-1)) % mod)
print(*ans, sep='\n')ABC265 G - 012 Inversion
x ★ 遅延セグ木のムズい問題でACするまで苦労したが、セグ木の理解が進んでよかった。セグ木っていろんなモノを載せて処理できるんだなぁと実感できた。セグ木においては、そのノードに対して何かしらの作用をするわけだが、これまで出てきた、数字を変更する、数字に加える、などシンプルなものに留まらない。まず、本問題では、保持する値が、[0の数, 1の数, 2の数, (1,0)の数, (2,0)の数, (2,1)の数]という6つの値である。セグ木の基本0、各ノードが値を持つ。セグ木の基本1、範囲と範囲を結合した値(積と呼ぼう)を計算できる。確かにこれでいける。解説参考。なお、[0,0,0,0,0,0]が単位元として機能する。
def prod(self, x, y):
ret = [0]*6
ret[0] = x[0] + y[0]
ret[1] = x[1] + y[1]
ret[2] = x[2] + y[2]
ret[3] = x[3] + y[3] + x[1] * y[0]
ret[4] = x[4] + y[4] + x[2] * y[0]
ret[5] = x[5] + y[5] + x[2] * y[1]
return retセグ木の基本2、作用させた結果を計算できる。確かにいける。この問題では、0,1,2をそれぞれs,t,uに変更した時、値がどのように変化するか?
def mapping(self, f, x):
ret = [0]*6
ret[f[0]] += x[0]
ret[f[1]] += x[1]
ret[f[2]] += x[2]
cnt = [[0]*3 for _ in range(3)]
cnt[f[1]][f[0]] += x[3]
cnt[f[2]][f[0]] += x[4]
cnt[f[2]][f[1]] += x[5]
cnt[f[0]][f[1]] += x[0] * x[1] - x[3]
cnt[f[0]][f[2]] += x[0] * x[2] - x[4]
cnt[f[1]][f[2]] += x[1] * x[2] - x[5]
ret[3] = cnt[1][0]
ret[4] = cnt[2][0]
ret[5] = cnt[2][1]
return ret遅延セグ木の基本3、作用と作用を結合できる。遅延セグ木における遅延情報とは、そのノードの子にまだ作用させていないという意味。その遅延情報に親から伝搬してきたり、状態を変化させる命令が来たときに、作用と作用を結合したものに更新する必要がある。遅延セグ木の基本4、自分自身とその先祖にあたるノードの情報は最新状態になっており、子は最新状態にないっていない。そして、必要なときに伝搬させる情報を遅延情報として保持する。ようやく全体像をつかんで実装したあと、ACx4、WAx18とWAが大量発生してデバッグに苦労したが、原因は、上のprodは、交換法則が成り立たないことを見逃していたことだった。和も最大値もGCDも交換法則が成り立つので油断していたが、ここは左右の順序が意味をなしていても扱えるのだった。Wikipediaの交換法則のページを見ると、交換法則が成り立たない例として「行列の乗算」「3次元数ベクトルのベクトル外積」「写像の合成」が挙げられていた。外積は結合できないのでないが、行列乗算と写像の合成はあるかなと思った。orange #遅延セグ木 2023-09-04
ABC265 F - Manhattan Cafe
x ★内容はなんか典型問題な気もするけど激ムズ。N = 100(次元数)、D = 1000(マンハッタン距離)。計算量は、O(N D^2)。制限時間が6秒となっている。自分のPythonコードは3.5秒くらいだった。自力では頭の中で全然整理できなかった。しかしこれ、典型的なDP問題と言えるのかも。取りうる座標は、各次元1000x1000あるので、普通に全部調べると1000000^100という無茶苦茶な計算量になる。しかし1次元ごとに1000x1000の状態を持ち、それを分岐させずに次の次元の1000x1000の状態に遷移することで、100乗ではなく、100倍の計算量に縮約できる。この考え方は、直前にやったABC263 Fと全く同じ気がする。連続でやったことで定着すればいいな。すべてのパターンに分岐させずに、少ない状態数にまとめてしまう。これこそがDPの本質なのかも。この問題の考え方は、1次元ずつ順番に座標を決めていって、d次元目では、マンハッタン距離1000のうちPからとQからそれぞれ、i、j使った場合の数を更新していく。で、rの座標はpとqの座標の差によってきまり、i-j平面上で斜めの直線上の値のみから遷移することがわかるので、斜めの累積和を計算しておくことで、遷移をO(N)からO(1)に減らせる。この処理を入れなければO(N D^3)で、当然TLEになってしまう。yellow #DP 2023-07-12
M = 998244353
N, D = map(int, input().split())
P = list(map(int, input().split()))
Q = list(map(int, input().split()))
size = (D+1)*(D+1)
def idx(i, j):
return i + j * (D+1)
dp = [0]*size
px, qx = P[0], Q[0]
boaders = [px-D, px+D, qx-D, qx+D]
boaders.sort()
for rx in range(boaders[1], boaders[2]+1):
dp[idx(abs(px-rx), abs(qx-rx))] += 1
sumu = [0]*size # up
sumd = [0]*size # down
for d in range(1, N):
for s in range(2*D+1):
j = min(s, D)
i = s - j
idx_ = idx(i, j)
sumd[idx_] = dp[idx_]
i, j, idx_ = i+1, j-1, idx_-D
while i <= D and j >= 0:
sumd[idx_] = (sumd[idx_+D] + dp[idx_]) % M
i, j, idx_ = i+1, j-1, idx_-D
for s in range(-D, D+1):
j = max(0, s)
i = j - s
idx_ = idx(i, j)
sumu[idx_] = dp[idx_]
i, j, idx_ = i+1, j+1, idx_+D+2
while i <= D and j <= D:
sumu[idx_] = (sumu[idx_-D-2] + dp[idx_]) % M
i, j, idx_ = i+1, j+1, idx_+D+2
ndp = [0]*size
s = abs(P[d] - Q[d])
for i in range(D+1):
for j in range(D+1):
si = max(0, i-s)
sj = i + j - si - s
if 0 <= sj:
tj = max(0, j-s)
ti = i + j - tj - s
ndp[idx(i, j)] += sumd[idx(ti, tj)] - (0 if si == 0 or sj == D else sumd[idx(si-1, sj+1)])
if ti > 0 and tj > 0:
ndp[idx(i, j)] += sumu[idx(ti-1, tj-1)]
if si > 0 and sj > 0:
ndp[idx(i, j)] += sumu[idx(si-1, sj-1)]
ndp[idx(i, j)] %= M
dp = ndp
print(sum(dp) % M)ABC264 G - String Fair
x グラフになると思ったけど、考察詰められず。WAも出しまくって、手こずってしまった。1文字追加すると美しさは、ラスト1文字、2文字、3文字のTがあればその分変化する。なのでラスト2文字(XY)を状態とし、(YZ)へ変化する場合の美しさの変化をすべて計算できる。で、最大の美しさだが、ベルマンフォードだという。無限上昇する閉路があれば収束しないので、ベルマンフォードなら検出できる。収束すれば最大値が求まる。Bellman-Fordは最短経路を求めるために使うと思い込んでると、解けないので、思いつくのは難しいと思う。yellow #ベルマンフォード 2023-08-26
import sys
IN = int(input())
N = 703
ORDA = ord('a')
edges = [[[(v%26)*26+c, 0] for c in range(26)] for v in range(N-1)]
edges.append([[676+c, 0] for c in range(26)]) # [702] is '$$'
for _ in range(IN):
t, p = input().split()
p = int(p)
if len(t) == 1:
c = ord(t) - ORDA
for v in edges:
v[c][1] += p
elif len(t) == 2:
c1 = ord(t[0]) - ORDA
c2 = ord(t[1]) - ORDA
for frm in range(c1, N-1, 26):
edges[frm][c2][1] += p
else:
c1 = ord(t[0]) - ORDA
c2 = ord(t[1]) - ORDA
c3 = ord(t[2]) - ORDA
edges[c1*26+c2][c3][1] += p
INF = 10**15
S = N-1
dist = [-INF]*N
dist[N-1] = 0
move = 0
while True:
update = False
for frm in range(N):
for to, c in edges[frm]:
if dist[frm] != -INF and dist[to] < dist[frm] + c:
dist[to] = dist[frm] + c
update = True
move += 1
if not update:
break
if move > N-1:
print('Infinity')
sys.exit()
ans = -INF
for i in range(N-1):
ans = max(ans, dist[i])
print(ans)ABC263 G - Erasing Prime Pairs
x 足して素数になる数字は2つのグループに分けられる。なぜなら2以外の素数は奇数だから。よって、2部グラフを作って最大フロー問題を解けばいいと気づいて、すげーこんなの気づけるようになったよー。と喜んでたら、罠があって、結局自力で解けなかった。1もたくさんあるので、1と1を組み合わせて素数の2を作って消すことができることすら最初きづいてなかった。この問題は1をどう扱うか?が肝であり、それがわかってない時点で全然わかってないということが判明。甘すぎた。最大流を流す、が、1はできるだけ使わずに流したほうが良い。1は1同士で消せるから。1をできるだけ使わない最大流をどう求めるのか?最小費用流で解くという解法もあった。見ていないけど、1にコストを設定すれば、1をできるだけ使わないようにできそうと思うのは自然な発想かもしれない。しかし1ずつ流量増やすのかな?その辺詰めきれない気がするので、今は考えないことにしよう。kyopro_friendsさんの解説がわかりやすかったのでこれを使った。この解説、最大流のアルゴリズムを理解していて、その中身について考えなければ理解できないだろう。1を使わずに最大流を求める。1を使って最大流を求める。この差分が、最大流において、1に流す最小の流量であると。確かに最大流のアルゴリズムは、SからTに流せるだけ流していくという方法なので、1を使わずに流したフローを1を使ったときに押し戻すことはない。他に自分で考えたらどのようなやり方が思いつくかなーと考えてみると、1も含めて最大流を流し、できるだけ1を減らすために1からSに向かって進む閉ループを見つけて流せるだけ流す。という方法もありうるかもしれないと思った。実装する気力ないが。この問題において、何を問われているのか?理解するのが難しい問題だった。それはそうと、最大流でINFFLOWを十分でかくしないと無限ループしてTLEすることにも気づいた。そういうミスしないの大事。最終的に98msでPython勢のベスト3の速度を出すことができた。TLE連発の苦しみを乗り越え、これは満足。yellow #最大流 2023-08-23
N = int(input())
AB = [tuple(map(int, input().split())) for _ in range(N)]
AB.sort(key=lambda x:x[0])
G = [[] for _ in range(N)]
def prime(x):
i = 2
while i * i < x:
if x % i == 0:
return False
i += 1
return True
for i in range(N-1):
for j in range(i+1, N):
if prime(AB[i][0] + AB[j][0]):
G[i].append(j)
G[j].append(i)
used = [0]*N # 1 or 2
for v in range(N):
if used[v] == 0:
stack = [v]
used[v] = 1
while stack:
cur = stack.pop()
for nex in G[cur]:
if used[nex] == 0:
stack.append(nex)
used[nex] = (2 if used[cur] == 1 else 1)
S, T = N, N+1
mf = MF(N+2)
for i in range(N):
if used[i] == 1:
mf.add_edge(S, i, AB[i][1])
for nex in G[i]:
mf.add_edge(i, nex, AB[i][1])
else:
mf.add_edge(i, T, AB[i][1])
if AB[0][0] == 1:
mf.g[S][0][1] = 0
ans = mf.mf(S, T)
mf.g[S][0][1] = AB[0][1]
f1 = mf.mf(S, T)
ans += f1 + (AB[0][1] - f1) // 2
else:
ans = mf.mf(S, T)
print(ans)ABC263 F - Tournament
x ★むずかしい。全パターン試そうとすると1回戦から2^(2^N)通りとかになって、全く間に合わないなぁ。と、こういうときってDPなのかもしれない。DP使うと縮退するよね。この問題は実際DPで解ける。DP[i][j]でi回目にjが勝ち進んだ場合の獲得賞金の最大値を管理すると解ける。細かいところ詰めるのはちょっと大変だけど、がんばろう。yellow 2023-07-10
N = int(input())
C = [[0] + list(map(int, input().split())) for _ in range(2**N)]
dp = [[0]*(2**N) for _ in range(N+1)] # i == 1 all 0
for i in range(2, N+1):
children = [0]*(2**(N-i+1))
for g in range(2**(N-i+1)):
j0 = g * 2**(i-1)
for j in range(j0, j0 + 2**(i-1)):
children[g] = max(children[g], dp[i-1][j] + C[j][i-1]) # 勝ち進んで負ける
for g in range(2**(N-i+1)):
other = g+1 if g % 2 == 0 else g-1
j0 = g * 2**(i-1)
for j in range(j0, j0 + 2**(i-1)):
dp[i][j] = dp[i-1][j] + children[other]
ans = 0
for j in range(2**N):
ans = max(ans, dp[N][j] + C[j][N])
print(ans)ABC262 G - LIS with Stack
x ★ 激ムズDP。これを考えるちょっと前に、ABC261 Gを解説ACしてたので、ちょっと似てそうな激ムズDPつながりということで、ABC261 Gをヒントにして考え抜けば、道が開けないかなぁ?と思って考えてたが、無理だった。この問題、解説ACすると実装がずいぶん軽いが、コンテスト中に18人しか解けていない。つまり実装が大変なタイプと言うより、考察が大変で解かれなかったのだろうから、考え方を学ぶことで得られることが多いかもしれない。しかし、解説を読んで、あぁそうかぁとならず、AC後も、どう考察したらこんな方針になるんだよと思う。反省しがいがあるというもの。なんでそうなるんですかねぇ。でかい数字は最後にXに追加するというのが着眼点らしい。これにいきなり気づく必要があるのなら難しいかも。よって使う最大数値を固定するという考え方から、使う最大数値で遷移するDPか?と思う可能性があるのかも。区間にある、どれかの最大数値の前後に分けると、前で使う数字の最大値より、後ろで使う最大値の方が小さくない必要があると気付ける。すると使う最小値も必要なのか?と思うのかも。必要と気づけたところで、遷移を構築できる気はしないが。ただ、最大値の前後の関係が導けたので、幅を広げていく区間DPがいいかな?ということも気付ける。これで一応4次元が確定して、しかも十分でもあるのだから。ここからは遷移を正しく構築できるか?だ。確信がなくてもやるしかない。自信を持って使う数字の範囲を固定したDPを構築するとしよう。幅1の値は求められる。幅1の値が求まれば、2以上の場合も求まるか?このコードACできてるけど、やっぱりなんか変じゃない?nはkより大きい場合があるのに、小さい順のkでループしながらn使ってない?って思ったら、最大値lをインデックスmで使う場合を調べてるので、区間がより狭い場合しか見ないんだ。確かにこのDPは成立しているぞ。より狭い区間の計算は終わっていて、その中の3次元目、4次元目の値は全部使ってOK!いけそう。区間DPでたまに気になるんだけど、両側にはみ出した時、アクセス例外を避けるために条件分岐すると重くなるから、ダミーインデックスを伸ばしておいて、条件分岐不要にしてる。これ結構効くよね。順序逆転した異次元領域はどうせ0だから突っ込んでいってもいいとか。笑。red #DP #区間DP 2023-09-25
N = int(input())
A = list(map(int, input().split()))
a2x = {a: i+1 for i, a in enumerate(sorted(set(A)))}
A = [-1] + [a2x[a] for a in A] # use 1-N
maxa = max(A) # val is 1-maxa
dp = [[[[0]*(maxa+1) for _ in range(maxa+1)] for _ in range(N+2)] for _ in range(N+2)]
for i in range(1, N+1):
for k in range(1, A[i]+1):
for l in range(A[i], maxa+1):
dp[i][i][k][l] = 1
for leng in range(2, N+1):
for i in range(1, N - leng + 2):
j = i + leng - 1
for k in range(1, maxa+1):
for l in range(k, maxa+1):
dp[i][j][k][l] = dp[i][j][k][l-1]
for m in range(i, j+1):
if A[m] == l:
for n in range(k, l+1):
dp[i][j][k][l] = max(dp[i][j][k][l], 1 + dp[i][m-1][k][n] + dp[m+1][j][n][l])
print(dp[1][N][1][maxa])ABC262 F - Erase and Rotate
o むずかしい。オイラーツアー以来の位置情報付きセグ木で解いた。バグりまくって頭混乱して時間かかってイライラした。難しいなぁやっぱ黃Diffは。解き方が完全にわかっても、そこからの詰めでミスったら時間かかってACできないんだよな。めずらしく無限ループでのTLEも出してしまった。yellow 2023-07-08
# セグ木略
N, K = map(int, input().split())
Kcopy = K
P = list(map(int, input().split()))
if K == 0:
print(*P)
sys.exit()
segt = SEGTRMQ(N)
for i, p in enumerate(P):
segt.set(i, p)
m1, i1 = segt.query(0, K+1)
m2, i2 = segt.query(N-K-1, N)
ans1 = []
ans2 = []
if m1 <= m2:
prev = 0
while True:
K -= i1 - prev # removed
prev = i1 + 1
ans1.append(m1)
if K == 0:
ans1.extend(P[prev:])
break
elif K >= N - prev:
break
m1, i1 = segt.query(prev, prev + K + 1)
K = Kcopy
if i2 != 0 and m1 >= m2:
P = P[i2:] + P[:i2]
posi = N - i2
segt2 = SEGTRMQ(N)
for i, p in enumerate(P):
segt2.set(i, p)
K -= 1
prev = 1
ans2.append(P[0])
while True:
if K == 0:
ans2.extend(P[prev:])
break
elif K >= N - prev:
break
m2, i2 = segt2.query(prev, prev + K + 1)
K -= i2 - prev
prev = i2 + 1
ans2.append(m2)
if i2 < posi:
K -= 1
if not ans2 or ans1 and ans1 < ans2:
print(*ans1)
else:
print(*ans2)ABC261 G - Replace
x ★ 激ムズ。1ヶ月ぶりの赤Diffトライ。最初自力でACするぞーと意気込んで、一応アルゴリズムをちゃんと組み立てて提出まで持ち込んだが、ねばったものの、TLEx5がベストの結果で、ACには至らず。1週間がんばったが諦めた。実はTLEするテストケースで実際に自分のマシン上で実行して、それなりの実行速度が出ていたので、おそらくもうちょっとだったと思う。ローカルでの時間より、AtCoderのサーバーでの時間がだいぶ短くなるという経験があるので。これならC++で同じロジックを組めば、ACできる気がする。しかし再帰関数を使っていたというのが良くないのと、解説のロジックだとだいぶ高速化したので、だめなんだろう。認めなければ。自力コードはこれ。コードなが。再帰呼出しでメモ化してがんばったりしたんだよなw 力尽きた。
from collections import defaultdict, deque
ORDA = ord('a')
INF = 10**15
S = tuple(ord(c) - ORDA for c in input())
T = tuple(ord(c) - ORDA for c in input())
K = int(input())
single = defaultdict(dict)
double = defaultdict(dict)
for _ in range(K):
c, a = input().split()
c = ord(c) - ORDA
a = tuple(ord(x) - ORDA for x in a)
if len(a) == 1:
single[c][a[0]] = 1
elif len(a) <= len(T): # len(a) > 1
double[c][a] = 1
single_ = defaultdict(dict)
for c in range(26):
if c not in single:
continue
dist = [-1]*26
dist[c] = 0
q = deque([c])
while q:
cur = q.popleft()
if cur in single:
for nex in single[cur]:
if dist[nex] == -1:
dist[nex] = dist[cur] + 1
q.append(nex)
for i in range(26):
if dist[i] > 1:
single_[c][i] = dist[i]
for c in single_:
single[c].update(single_[c])
double_ = defaultdict(dict)
for c in single:
for to, cost in single[c].items():
for toto in double[to]:
if toto in double_[c]:
double_[c][toto] = min(double_[c][toto], cost + 1)
else:
double_[c][toto] = cost + 1
for c in double_:
for to in double_[c]:
if to in double[c]:
double[c][to] = min(double[c][to], double_[c][to])
else:
double[c][to] = double_[c][to]
doublesort = [[] for _ in range(26)]
for c, d in double.items():
doublesort[c] \
= sorted([(s, cost) for s, cost in d.items()], key=lambda x: len(x[0]))
tr2t = [[tuple()]*(len(T)+1) for _ in range(len(T))]
for i in range(len(T)):
for j in range(i+1, len(T)+1):
tr2t[i][j] = T[i:j]
single_matrix = [[INF]*26 for _ in range(26)]
for i in range(26):
single_matrix[i][i] = 0
for frm in single:
for to in single[frm]:
single_matrix[frm][to] = single[frm][to]
check_s_ret = {}
check_ret = {}
def check_s(a, trange): # single a -> t
global check_s_ret, T
ret = INF
tl, tr = trange
lent = tr-tl
if lent == 1:
return single_matrix[a][T[tl]]
else:
if (a, tr2t[tl][tr]) in check_s_ret:
return check_s_ret[(a, tr2t[tl][tr])]
for s, cost in doublesort[a]:
if len(s) > lent:
break
if cost >= ret:
continue
cur = check(s, trange)
if cur < INF:
ret = min(ret, cur + cost)
check_s_ret[(a, tr2t[tl][tr])] = ret
return ret
def check(s, trange):
global check_ret
ret = INF
tl, tr = trange
lens, lent = len(s), tr-tl
if lens == lent and s == tr2t[tl][tr]:
return 0
if (s, tr2t[tl][tr]) in check_ret:
return check_ret[(s, tr2t[tl][tr])]
dp = {}
for j in range(lent - lens + 1):
if j == 0:
cur = single_matrix[s[0]][T[tl]]
else:
cur = check_s(s[0], (tl, tl+j+1))
if cur < INF:
dp[j] = cur
if dp:
for i in range(1, lens-1):
ndp = defaultdict(lambda: INF)
for pj, prev in dp.items():
for j in range(pj + 1, lent - lens + i + 1):
if j == pj+1:
cur = single_matrix[s[i]][T[tl+pj+1]]
else:
cur = check_s(s[i], (tl+pj+1, tl+j+1))
if cur < INF:
ndp[j] = min(ndp[j], prev + cur)
if not ndp:
break
else:
dp = ndp
else:
for pj, prev in dp.items():
if pj == lent-2:
cur = single_matrix[s[-1]][T[tr-1]]
else:
cur = check_s(s[lens-1], (tl+pj+1, tr))
if cur < INF:
ret = min(ret, prev + cur)
check_ret[(s, tr2t[tl][tr])] = ret
return ret
ans = INF
if len(S) == 1:
ans = check_s(S[0], (0, len(T)))
else:
ans = check(S, (0, len(T)))
print(ans if ans != INF else -1)苦労した解説AC。まだこう考えれば上の再帰呼出しではなく、このようなDPを導けるのか?必要最小限のデータはなんなのか?わかり切っていない。まだまだ反省すべき点のある問題である。 red #DP 2023-09-17
import heapq
from collections import deque
ORDA = ord('a')
INF = 10**15
S = tuple(ord(c) - ORDA for c in input())
T = tuple(ord(c) - ORDA for c in input())
lenS, lenT = len(S), len(T)
K = int(input())
CA = []
single = [] # store ids
double = []
maxL = lenS
for k in range(K):
c, a = input().split()
c = ord(c) - ORDA
a = tuple(ord(x) - ORDA for x in a)
CA.append((c, a))
if len(a) == 1:
single.append(k)
elif len(a) <= len(T): # len(a) > 1
maxL = max(maxL, len(a))
double.append(k)
singledists = [[INF]*26 for _ in range(26)]
graph = [[] for _ in range(26)]
for k in single:
c, a = CA[k]
graph[c].append(a[0])
for c in range(26):
dists = singledists[c]
dists[c] = 0
q = deque([c])
while q:
cur = q.popleft()
for nex in graph[cur]:
if dists[nex] == INF:
q.append(nex)
dists[nex] = dists[cur] + 1
dp = [[[[INF]*(maxL+1) for _ in range(K+1)] for _ in range(lenT)] for _ in range(lenT)]
dpc = [[[INF]*26 for _ in range(lenT)] for _ in range(lenT)]
for i in range(lenT)[::-1]:
if i == 0: # add S finally
CA.append((26, S))
if lenS > 1:
double.append(K)
else:
single.append(K)
K += 1
for j in range(i, lenT): # watch T[i:j+1]
if i == j:
for k in range(K):
c, a = CA[k]
dp[i][j][k][1] = singledists[a[0]][T[i]]
for c in range(26):
dpc[i][j][c] = singledists[c][T[i]]
else: # i < j
for k in double:
c, a = CA[k]
for l in range(2, len(a)+1)[::-1]:
for m in range(i+l-2, j):
dp[i][j][k][l] = min(dp[i][j][k][l], dp[i][m][k][l-1] + dpc[m+1][j][a[l-1]])
start = 27
edges = [[] for _ in range(28)] # 26 is dummy for S, 27 is start
for k in single:
c, a = CA[k]
edges[a[0]].append((c, 1))
for k in double:
c, a = CA[k]
if dp[i][j][k][len(a)] != INF:
edges[start].append((c, dp[i][j][k][len(a)] + 1))
dists = [INF]*(28)
pq = [(0, start)]
while pq:
d, cur = heapq.heappop(pq)
if INF != dists[cur]:
continue
dists[cur] = d
for nex, c in edges[cur]:
if INF == dists[nex]:
heapq.heappush(pq, (d + c, nex))
for k in range(K):
c, a = CA[k]
dp[i][j][k][1] = dists[a[0]]
for c in range(26):
dpc[i][j][c] = dists[c]
if dp[0][lenT-1][K-1][lenS] == INF:
print(-1)
else:
print(dp[0][lenT-1][K-1][lenS] )ABC260 G - Scalene Triangle Area
x 3方向に累積和を取って、スライドさせたときに増減を計算すれば、いけるなぁと思ったので、その方針でやろうとしたが、あまりにも面倒で実装に手間取り、時間がかかったのでやる気が失せてしまった。解説をみるとなんと、いもす法らしい。3方向にいもす法をやる。初めて見たので混乱したけど、たしかにこれで守っている範囲を表現できる。実装もスッキリ楽にできた。しかし最初ミスったのは、いもす法において、入り口と出口があるけど、出口は省略可、入り口は省略不可ということ。まあ当たり前だけど。普段は意識しなくて良いだろうけど、今回はx,yどちらかが減少する方向にいもすの累積和を計算しなければならないので、入り口が範囲外だったばあい、境界に移動してセットしなければならない。そこは気をつける必要があった。また勉強になったなぁ。yellow #いもす 2023-08-26
N, M = map(int, input().split())
S = [[1 if c == 'O' else 0 for c in list(input())] for _ in range(N)]
imos = [[0]*N for _ in range(N)]
for s in range(N):
for t in range(N):
if S[s][t] == 0:
continue
imos[s][t] += 1
if s-1 >= 0 and t+2 < N:
imos[s-1][t+2] -= 1
if s+M < N:
imos[s+M][t] -= 1
if t+2 < N:
imos[s+M][t+2] += 1
else: # s+M >= N
d = s+M - (N-1)
if t + 2*d < N:
imos[N-1][t+2*d] -= 1
if t + 2*(d+1) < N:
imos[N-1][t+2*(d+1)] += 1
if t+2*(M+1) < N:
imos[s][t+2*(M+1)] -= 1
if s-1 >= 0:
imos[s-1][t+2*(M+1)] += 1
for s in range(N-1)[::-1]:
for t in range(2, N):
imos[s][t] += imos[s+1][t-2]
for s in range(1, N):
for t in range(N):
imos[s][t] += imos[s-1][t]
for s in range(N):
for t in range(1, N):
imos[s][t] += imos[s][t-1]
Q = int(input())
ans = []
for _ in range(Q):
x, y = map(int, input().split())
ans.append(imos[x-1][y-1])
print(*ans, sep='\n')ABC259 G - Grid Card Game
x やはり難しい。燃やす埋める的な、フローで解く問題っぽいなぁと思って考えてたけど、結局どのようなグラフを構成すればいいか?自分で導くことはできなかった。結局のところ、燃やす埋めると同じ考え方でグラフを構成して、最大フロー=最小カットで、解く問題だった。そうわかっていても、グラフを構成するのが難しい。こうして1度ACしても、まだ、次できる自信を持てていない。燃やす埋めるでは、SとTの間に頂点は1つだが、この問題では2つある。i行とj列に着目する。画像の上から順に、i行目だけ選ぶ、i行目もj列目も選ばない、j列目だけ選ぶ、i行目もj列目も選ぶ、に対応したカットと考えることができる。iもjも選んだ場合は、iもjも選ばない真ん中の辺に流れないので、整合性が取れている。(i,j)が負だった場合は、iもjも選ぶ場合のコストを∞とする必要があるので、jからiに∞の辺を張ることで、最小カットになりえないことを表現できる。このグラフを作るために、辺のコストが正になるように持っていかなければならない。得点の初期値を、正の数字の合計とし、i行を選択するコストをi行の負数の和、j列を選択するコストをj行の負数の和、i行もj行も選択しないコストを(i,j)の値とする。この持っていきかたが、結構難しいと感じてる。orange #燃やす埋める #最小カット #最大流 2023-09-05
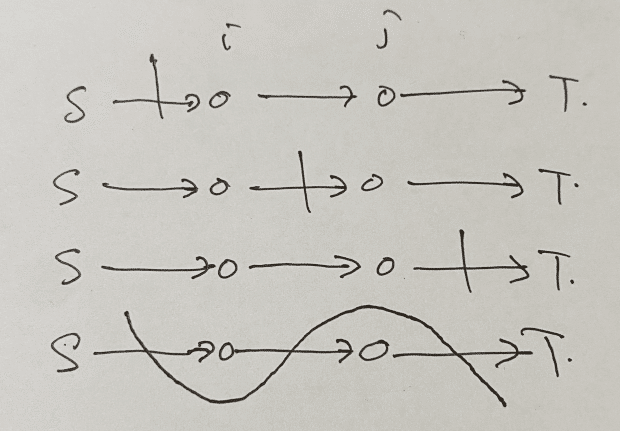
INF = 10**16
H, W = map(int, input().split())
mf = MF(H+W+2)
S, T = 0, H+W+1
A = [list(map(int, input().split())) for _ in range(H)]
plus_total = 0
minus_h = [0]*H
minus_w = [0]*W
for i in range(H):
i_ = i + 1
for j in range(W):
j_ = j + H + 1
a = A[i][j]
if a < 0:
minus_h[i] -= a
minus_w[j] -= a
mf.add_edge(j_, i_, INF)
elif a > 0:
plus_total += a
mf.add_edge(i_, j_, a)
for i in range(H):
mf.add_edge(S, i+1, minus_h[i])
for j in range(W):
mf.add_edge(j+H+1, T, minus_w[j])
print(plus_total - mf.mf(S, T))ABC258 F - Main Street
x 共通処理を関数でちゃんと書いて整理しなければ、混乱してわけがわからなくなる問題。難しい。整理してこうなったが、まだミスりそう。実際最後バグになかなか気づかなくて苦労した。これをミスらずに書くのは相当な注意を要する。yellow 2023-07-05
INF = 10**20
T = int(input())
def manhattan(a, b): # v2, v2
return abs(a[0]-b[0]) + abs(a[1]-b[1])
def gg_mintime(a, b, B): # (v2,t), (v2,t) return the least time
p1, t1 = a
p2, t2 = b
if p1[0] == p2[0] and p1[0] % B == 0:
return abs(p1[1]-p2[1]) + t1 + t2
elif p1[1] == p2[1] and p1[1] % B == 0:
return abs(p1[0]-p2[0]) + t1 + t2
else:
q1 = []
if p1[0] % B == 0:
d = (p1[1]//B)*B
q1.extend([((p1[0], d), p1[1]-d+t1), ((p1[0], d+B), d+B-p1[1]+t1)])
else: # p1[1] % B == 0
l = (p1[0]//B)*B
q1.extend([((l, p1[1]), p1[0]-l+t1), ((l+B, p1[1]), l+B-p1[0]+t1)])
q2 = []
if p2[0] % B == 0:
d = (p2[1]//B)*B
q2.extend([((p2[0], d), p2[1]-d+t2), ((p2[0], d+B), d+B-p2[1]+t2)])
else: # p2[1] % B == 0
l = (p2[0]//B)*B
q2.extend([((l, p2[1]), p2[0]-l+t2), ((l+B, p2[1]), l+B-p2[0]+t2)])
mintime = INF
for a in q1:
p1, t1_ = a
for b in q2:
p2, t2_ = b
mintime = min(mintime, manhattan(p1, p2) + t1_ + t2_)
return mintime
anss = []
for _ in range(T):
B, K, sx, sy, gx, gy = map(int, input().split())
a = []
ans = K*manhattan((sx,sy), (gx,gy))
if sx % B == 0 or sy % B == 0:
a.append(((sx, sy), 0))
else:
sl = (sx//B)*B
sd = (sy//B)*B
a.extend([((sl, sy), K*(sx-sl)), ((sl+B, sy), K*(sl+B-sx))])
a.extend([((sx, sd), K*(sy-sd)), ((sx, sd+B), K*(sd+B-sy))])
b = []
if gx % B == 0 or gy % B == 0:
b.append(((gx, gy), 0))
else:
gl = (gx//B)*B
gd = (gy//B)*B
b.extend([((gl, gy), K*(gx-gl)), ((gl+B, gy), K*(gl+B-gx))])
b.extend([((gx, gd), K*(gy-gd)), ((gx, gd+B), K*(gd+B-gy))])
for i, s in enumerate(a):
for j, t in enumerate(b):
ans = min(ans, gg_mintime(s, t, B))
anss.append(ans)
print(*anss, sep='\n')ABC257 G - Prefix Concatenation
o ★Z Algorithmからの配るDP。間に合わないと思ったけどよく考えたら1度確定した回数は覆らないので更新不要で間に合う…。ちょっと不思議な問題。つまり、1つ目のprefixで行けるところは2つ目で行けますって更新する必要がない。1つ目で行けるんだから。minimum確定。で、順番に見て行って、確定したところより、先に進める場合に、n+1個目のprefixで行けるという情報を更新する。なので、Tのすべての文字を1回しか更新しないので、DP部分は、O(|T|)となる。Z AlgorithmがO(|S|+|T|)なので、高速に処理できる。yellow #zalgorithm 2023-08-04
S = list(input())
N = len(S)
T = list(input())
X = S + [','] + T
M = len(X)
z = z_algorithm(X)
ans = [0]*M
for i in range(N+1, N+1+z[N+1]):
ans[i] = 1
j = N+1+z[N+1] # not fix next
for i in range(N+2, M):
if ans[i-1] == 0:
continue
if i + z[i] - 1 < j:
continue
for j_ in range(j, i + z[i]):
ans[j_] = ans[i-1] + 1
j = i + z[i]
print(ans[M-1] if ans[M-1] > 0 else -1)ABC256 G - Black and White Stones
o これも昔から考えたらかなり難しい黄Diffだけど、自力でいけた。最初、行列計算が遅くてTLEx5を解消できなかったけど、中身をループを使わずに展開したらギリギリ通った。それでも遅いけど。さらに行列を1次元リストにした方がいいとかあるかもしれない。N次元行列の掛け算を展開したライブラリを用意しておいたほうが良いとか、そういう話ではあるんだけど、まあいいや。あ、あとこの問題N=1兆なんだけど、1兆とか出てきた時点でダブリングだなと改めて思うなどした。O(N)で解けないからO(Log N)なんだろうなぁ。と。1兆ステップが40ステップに減る。
M = 998244353
N, D = map(int, input().split())
COUNT_MAX = D
fact = [0]*(COUNT_MAX+1)
invfact = [0]*(COUNT_MAX+1)
fact[0] = 1
for i in range(1, COUNT_MAX+1):
fact[i] = fact[i-1] * i % M
invfact[COUNT_MAX] = pow(fact[COUNT_MAX], M-2, M)
for i in range(COUNT_MAX-1, 0, -1):
invfact[i] = invfact[i+1] * (i+1) % M
invfact[0] = 1
def choose(n, r):
return fact[n] * invfact[r] * invfact[n-r] % M
def multiply_mm(a, b):
res = [[0]*4 for _ in range(4)]
for i in range(4):
res[i][0] = (res[i][0] + a[i][0] * b[0][0] + a[i][1] * b[1][0] + a[i][2] * b[2][0] + a[i][3] * b[3][0]) % M
res[i][1] = (res[i][1] + a[i][0] * b[0][1] + a[i][1] * b[1][1] + a[i][2] * b[2][1] + a[i][3] * b[3][1]) % M
res[i][2] = (res[i][2] + a[i][0] * b[0][2] + a[i][1] * b[1][2] + a[i][2] * b[2][2] + a[i][3] * b[3][2]) % M
res[i][3] = (res[i][3] + a[i][0] * b[0][3] + a[i][1] * b[1][3] + a[i][2] * b[2][3] + a[i][3] * b[3][3]) % M
return res
def multiply_mv(a, v):
res = [0]*4
for i in range(4):
for j in range(4):
res[i] = (res[i] + v[j] * a[i][j]) % M
return res
ans = 0
for w in range(D+2):
A = choose(D-1, w) if w <= D-1 else 0
L = R = choose(D-1, w-1) if 1 <= w <= D else 0
B = choose(D-1, w-2) if 2 <= w else 0
ms = [[[A,A,0,0], [0,0,L,L], [R,R,0,0], [0,0,B,B]]]
step = 2
while step < N:
ms.append(multiply_mm(ms[-1], ms[-1]))
step *= 2
step = N-1
x = 0
matrix = [[1,0,0,0], [0,1,0,0], [0,0,1,0], [0,0,0,1]]
while step:
if step % 2 == 1:
matrix = multiply_mm(matrix, ms[x])
x += 1
step //= 2
temp1 = multiply_mv(matrix, [A,0,R,0])
temp2 = multiply_mv(matrix, [0,L,0,B])
ans = (ans + temp1[0] + temp1[1] + temp2[2] + temp2[3]) % M
print(ans)なんか遅かったので、解説を見ると、ぼくのコードが遅いのは別の原因があったようだ。上の方法では、4つの状態A(両端黒)、L(左だけ白)、R(右だけ白)、B(両方白)という4状態を遷移させていて、4x4行列の計算が必要となっていた。解説を見るとN角形の角の部分が白か黒かの2通りのパターンを遷移させていけば、2x2の行列計算で済む。これでむちゃくちゃ速くなる。辺で考えるとWW、WB、BW、BBの4パターン、頂点で考えるとWかBの2パターン。計算量がぜんぜん違う。重要。yellow #ダブリング #行列 2023-08-22
M = 998244353
N, D = map(int, input().split())
COUNT_MAX = D
fact = [0]*(COUNT_MAX+1)
invfact = [0]*(COUNT_MAX+1)
fact[0] = 1
for i in range(1, COUNT_MAX+1):
fact[i] = fact[i-1] * i % M
invfact[COUNT_MAX] = pow(fact[COUNT_MAX], M-2, M)
for i in range(COUNT_MAX-1, 0, -1):
invfact[i] = invfact[i+1] * (i+1) % M
invfact[0] = 1
def choose(n, r):
return fact[n] * invfact[r] * invfact[n-r] % M
def multiply_mm(a, b):
return [
(a[0] * b[0] + a[1] * b[2]) % M,
(a[0] * b[1] + a[1] * b[3]) % M,
(a[2] * b[0] + a[3] * b[2]) % M,
(a[2] * b[1] + a[3] * b[3]) % M
]
def multiply_mv(a, v):
return [
(v[0] * a[0] + v[1] * a[1]) % M,
(v[0] * a[2] + v[1] * a[3]) % M
]
ans = 0
for w in range(D+2):
A = choose(D-1, w) if w <= D-1 else 0
L = choose(D-1, w-1) if 1 <= w <= D else 0
B = choose(D-1, w-2) if 2 <= w else 0
ms = [[A,L, L,B]]
step = 2
while step <= N:
ms.append(multiply_mm(ms[-1], ms[-1]))
step *= 2
step = N
x = 0
matrix = [1,0, 0,1]
while step:
if step % 2 == 1:
matrix = multiply_mm(matrix, ms[x])
x += 1
step //= 2
temp1 = multiply_mv(matrix, [1, 0]) # black
temp2 = multiply_mv(matrix, [0, 1])
ans = (ans + temp1[0] + temp2[1]) % M
print(ans)ABC256 F - Cumulative Cumulative Cumulative Sum
x ★難しい。累積和の変化はセグ木で計算できそう。累積和の累積和なら遅延セグ木で計算できそう?でも累積和の累積和の累積和は無理だなぁとなった。これ、Aiの変化が累積和の累積和の累積和に何回影響するかの式を書き出してみると、Ai、Ai*i、Ai*i*iの3つの値の和を求めておけばよいことを導ける。おもしろい。ここまでは頭の中で絵を描いて考えても導けるけど、では?累積和の累積和の累積和の累積和だとどうなる?勉強のために計算できたほうが良い。10月、見直してたらまたムズかったw AiがDjに何回使われるかを計算すると、、、って話。iとjの式で表すと、AiとAi*iとAi*i^2の累積和が出てくる。よってそれをフェニック木で管理して…。という話。ムズい。式で書いてしまって、変形すればいけるよというやつ。yellow #式変形 #累積和 #フェニック木 2023-07-04
M = 998244353
class BIT():
def __init__(self, n):
self.n = n
self.sums = [0]*(n+1)
def add(self, i, input):
while i <= self.n:
self.sums[i] = (self.sums[i] + input) % M
i += i&-i
def prod(self, i):
'''return 0 if i == 0'''
res = 0
while i > 0:
res = (res + self.sums[i]) % M
i -= i&-i
return res
N, Q = map(int, input().split())
A = [0] + list(map(int, input().split()))
Ai0 = BIT(N)
Ai1 = BIT(N)
Ai2 = BIT(N)
for i in range(1, N+1):
Ai0.add(i, A[i])
Ai1.add(i, A[i]*i)
Ai2.add(i, A[i]*i*i)
inv2 = pow(2, M-2, M)
for _ in range(Q):
q = list(map(int, input().split()))
if q[0] == 1:
_, x, v = q
prev = A[x]
A[x] = v
Ai0.add(x, v-prev)
Ai1.add(x, (v-prev)*x)
Ai2.add(x, (v-prev)*x*x)
else:
_, x = q
print((Ai2.prod(x) - (2*x+3)*Ai1.prod(x) + (x+1)*(x+2)*Ai0.prod(x)) * inv2 % M)ABC255 G - Constrained Nim
o 自力でいけたー。今週月金で橙DIff連続で解いてるんだけど、昨日までの4問は激ムズで自力では解けなかった。それぞれ学びがかなりあってよかったけど、金曜日に自力ACで締められるのはうれしい。仕事も難しすぎて頭使いすぎてる上に、夜は強プロの難しい問題を毎日ねばってACして寝不足で疲れ切ってるから、もう休みたい。土曜のABCまで新しい問題は見ずに完全に気を緩めて休みたい。この問題は自然な考察で解法を導けた。Nimだが石の数A = 10^18で、Grundy数を順番に計算することは不可能。10^18だとダブリングでよく出てくる数字だけど、それはひっかけwで、石の取り方の制限がM = 200000あるので、この制限に関係する部分だけに注目することで、それ以外のスキマの部分のGrundy数は、あとで必要なときに計算して導けるのだろうと推測。小さい数字でGrundy数がどうなるか書いてみると、実際その通りでスキマの部分のGrundy数は数字が順番に並んでるだけで、あとで計算できるとわかる。2分探索を使ってO(Log M)で。制限に関係する部分の情報を構築するのはO(M Log M)、盤面のXORを計算するのはO(N Log N)なので、いける。ヨシッ!orange #Grundy数 #Nim 2023-09-08
import bisect
from collections import defaultdict
N, M = map(int, input().split())
A = list(map(int, input().split()))
R = defaultdict(list)
for _ in range(M):
x, y = map(int, input().split())
R[x].append(x-y)
expid = []
expval = []
expcount = defaultdict(int)
for x, tolist in sorted(R.items()):
exp = False
cand = x
if expid:
i = bisect.bisect_left(expid, x)
if i < len(expid) and expid[i] == x:
cand = expval[i]
else:
cand = x - i
toval_count = defaultdict(int)
for to in tolist:
if expid:
i = bisect.bisect_left(expid, to)
if i < len(expid) and expid[i] == to:
toval_count[expval[i]] += 1
else:
# i is expcount under to
toval_count[to - i] += 1
else:
toval_count[to] += 1
for val, c in toval_count.items():
if c == 1 and val not in expcount:
if val < cand:
exp = True
cand = val
else: # c > 1
if c == expcount[val] + 1:
if val < cand:
exp = True
cand = val
if exp:
expid.append(x)
expval.append(cand)
expcount[cand] += 1
xor = 0
for a in A:
if expid:
i = bisect.bisect_left(expid, a)
if i < len(expid) and expid[i] == a:
xor ^= expval[i]
else:
xor ^= a - i
if xor != 0:
print('Takahashi')
else:
print('Aoki')ABC254 G - Elevators
o ★ キタ━━━━(゚∀゚)━━━━!! 赤Diffをはじめて自力AC。めでたい。赤DiffのACはちょうど10問目という区切りでもある。テストケースtest_30を使ってデバッグしてなんとか。先週のABC261 Gも自力でいくぞと1週間ねばったけど、諦めてたので。今回はやりきった。デバッグがしんどかった。テストケースなしにデバッグできる気がしないので、反省はまだまだ必要だろう。セグ木入れてコードが200行近くになってしまったので、他の人より長い。非効率的な部分があるのだろうし。解説読んだ。考察の流れは同じだが、解説はその後DPで全部求めてしまってた。クエリのたびに毎回ダブリングしたけど間にあった。でもムズいよな。あまり考えたくない。 red #ダブリング 2023-09-22
import math
import bisect
from collections import defaultdict
N, M, Q = map(int, input().split())
# merge same building
imos = [defaultdict(int) for _ in range(N+1)]
for _ in range(M):
a, b, c = map(int, input().split())
imos[a][b] += 1
imos[a][c] -= 1
abc = []
noru = [[] for _ in range(N+1)]
oriru = [[] for _ in range(N+1)]
for a in range(1, N+1):
tmp = 0
ride = 0
for f, n in sorted(imos[a].items(), key=lambda x: x[0]):
if tmp == 0 and n > 0:
ride = f
tmp += n
if tmp == 0 and n < 0:
abc.append((a, ride, f))
noru[a].append(ride)
oriru[a].append(f)
fset = set() # only btm and top+1 are meaningful
tops = defaultdict(list) # top -> [(btm, bld)]
for a, b, c in abc:
fset.add(b)
fset.add(c+1)
tops[c].append((b, a))
flist = sorted(fset)
f2i = {f: i for i, f in enumerate(flist)}
segt = SEGT(len(flist))
for top in tops:
tops[top].sort(key=lambda x: x[0])
for btm, bld in tops[top]:
segt.set_(f2i[btm], top)
cango = [0]*len(flist)
cango_bld = [set() for _ in range(len(flist))]
for i, f in enumerate(flist):
cango[i] = segt.query(0, i+1)
if cango[i] > f:
for btm, bld in tops[cango[i]]:
if btm > f:
break
cango_bld[i].add(bld)
else:
cango[i] = 0 # cannot go even f+1
G = [[] for _ in range(len(flist))]
for i, f in enumerate(flist):
if cango[i] != 0:
igo = bisect.bisect_right(flist, cango[i]) - 1
if igo > i:
G[igo].append(i)
max_double = math.floor(math.log2(len(flist)))
parents = [[-2]*(len(flist)) for _ in range(max_double + 1)] # [0] parent, [1] granp
for i in range(len(flist))[::-1]:
if parents[0][i] == -2:
stack = [i]
parents[0][i] = -1
while stack:
cur = stack.pop()
for nex in G[cur]:
parents[0][nex] = cur
x = 0
while x < max_double:
if parents[x][parents[x][nex]] == -2:
break
parents[x+1][nex] = parents[x][parents[x][nex]]
x += 1
stack.append(nex)
ans = []
for _ in range(Q):
x, y, z, w = map(int, input().split()) # (x, y) -> (z, w)
if y == w:
if x == z:
ans.append(0)
else:
ans.append(1)
else:
if y > w:
x, y, z, w = z, w, x, y
# y < w
ty = y
tyup = False
if noru[x]:
ix = bisect.bisect_right(noru[x], y) - 1
if ix >= 0:
if y <= oriru[x][ix]:
ty = oriru[x][ix]
tyup = True
tw = w
twup = False
if noru[z]:
iz = bisect.bisect_right(noru[z], w) - 1
if iz >= 0:
if w <= oriru[z][iz]:
tw = noru[z][iz]
twup = True
if (tyup or twup) and ty >= tw:
if x == z:
ans.append(w-y)
else:
ans.append(w-y+1)
else: # ty -> tw
cur = bisect.bisect_right(flist, ty) - 1
goal = bisect.bisect_right(flist, tw) - 1
if cur < 0:
ans.append(-1)
else:
if cur == goal and cango[cur] != 0:
ans.append(w - y + 2)
continue
step = max_double
move = 0
while True:
while step >= 0 and parents[step][cur] < 0:
step -= 1
if step < 0:
ans.append(-1)
break
# step >= 0
while step >= 0 and parents[step][cur] >= goal:
step -= 1
if step == -1:
if parents[0][cur] >= goal:
move += 1
ans.append(w - y + move + 1)
break
else:
ans.append(-1)
break
cur = parents[step][cur]
move += 2**(step)
if cur >= goal:
ans.append(w - y + move + 1)
break
if step < 0:
ans.append(-1)
break
print(*ans, sep='\n')ABC253 G - Swap Many Times
o 自力ACいけた。以前1度やろうとしたことがあって、方針は立ったんだけど、実装しきれず、放置していた。なんかやり直したら、きれいに整理できて普通に1発ACできた。整理して実装しやすい方針を立てる技術は必要だけど、知らず知らずにも少しずつ身につくものなのかな。yellow 2023-08-22
N, L, R = map(int, input().split())
ans = list(range(1, N+1))
def mod1(i, j, k):
global ans
a = ans[:i]
b = [ans[i]]
c = ans[i+1:j]
d = ans[j:k]
e = [ans[k]]
f = ans[k+1:] if k+1 < N else []
ans = a + e + c + b + d + f
def mod2(i, l):
global ans
a = ans[:i]
b = ans[i:N-l]
c = ans[N-l:]
ans = a + list(reversed(c)) + b
L_, R_ = [-1, -1], [-1, -1]
count = 0
for i in range(1, N):
count += N - i
if count - N + i < L <= count:
L_ = [i-1, L - count + N - i]
if count - N + i < R <= count:
R_ = [i-1, R - count + N - i]
break
if L_[0] == R_[0]:
mod1(L_[0], L_[0]+L_[1], L_[0]+R_[1])
elif L_[0] + 1 == R_[0]:
mod1(L_[0], L_[0]+L_[1], N-1)
mod1(R_[0], R_[0]+1, R_[0]+R_[1])
else:
mod1(L_[0], L_[0]+L_[1], N-1)
mod2(L_[0]+1, R_[0]-1-L_[0])
mod1(R_[0], R_[0]+1, R_[0]+R_[1])
print(*ans)ABC253 E - Distance Sequence
o これも、昨日ABC245以降のGを埋め終わった影響で、抜けてて気になったのでやる。めっちゃ罠に引っかかってWAx2。K=0が罠だった。上下から累積和して、i+Kとi-Kの値が遷移するが、K=0のときは重なってしまうので、1回したカウントしてはならないという…。やらないつもりだったけど、やってみるもの。この問題をもって、ABC245からABC321までのEからGを全部埋めることができた。これからしばらくは、歯抜けを作らずに、ABC244以前をさかのぼりながらE、F、Gを順番にやっていこうかな。Diff順はなんか積み残しタスクを感じてしまうので。green #罠 2023-09-23
from itertools import accumulate
mod = 998244353
N, M, K = map(int, input().split())
dp = [[0]*(M+1) for _ in range(N)]
for a in range(1, M+1):
dp[0][a] = 1
for i in range(1, N):
ac0 = list(accumulate(dp[i-1]))
ac1 = list(accumulate(reversed(dp[i-1])))
ac1.reverse()
for a in range(1, M-K+1):
dp[i][a+K] = ac0[a] % mod
for a in range(K+1 if K != 0 else K+2, M+1):
dp[i][a-K] = (dp[i][a-K] + ac1[a]) % mod
print(sum(dp[N-1]) % mod)ABC252 G - Pre-Order
o 黄Diffだが自力ACできた。これ普通にやれるんだから結構力ついてるのかなぁとは思う。制約条件を確認し忘れて、問題読んでからランニングしながら考えてた。O(N^2)かと思って、これで解けるならN=3000くらいかなぁと予想しながら帰ってきて確認すると、O(N^3)でN=500だった。N^3重いのでは?と思ったが、定数倍が軽いらしい。部分木は必ず連続数列を使うので、区間DP的にやればいいと気づいた。とは言っても、dp[i][j]で部分木を表現するわけではないというひねりが入る。iがトップの部分木か、もしくはiが何かの子で弟がいる場合も合わせて数えていく。最初トップの場合と兄弟の場合を分けてdpする必要があるかと思ったが、遷移のときに常にまとめて使うことがわかるのでまとめて数える。ただし最後のdp[1]のときは1がトップの時だけを計算すれば良い。ヨシッ!yellow #区間DP #行きがけ #根付き木 2023-08-22
M = 998244353
N = int(input())
P = list(map(int, input().split()))
dp = [[0]*N for _ in range(N)]
dp[N-1][N-1] = 1
for i in range(1, N-1)[::-1]:
dp[i][i] = 1
for j in range(i+1, N):
dp[i][j] = dp[i+1][j]
if P[i+1] > P[i]:
dp[i][j] = (dp[i][j] + dp[i+1][j]) % M
for k in range(i+2, j+1):
if P[k] > P[i]:
dp[i][j] = (dp[i][j] + dp[i+1][k-1] * dp[k][j]) % M
print(dp[1][N-1])ABC251 G - Intersection of Polygons
x ★ 解けず。クエリの点を逆方向に移動して作った多角形(同じ形)を使ってなんとかするのか?みたいに思ったが、全然短時間で処理できる気がせず。とりあえず素直に式を書くと、簡単に式変形して計算量を減らせることに気づけるという。とにかく愚直な式を書いてみるのが教訓。クエリの点XがVj移動後の多角形の内部にあることを、このように表現できる。ただしxは、z座標0として外積を計算したz座標とする。笑。
(Pi+1 + Vj - Pi - Vj) x (X - Pi - Vj) >= 0
変形すると、Vj-Vjとか消えて、
(Pi+1 - Pi) x X >= (Pi+1 - Pi) x (Pi - Vj)
これが、i = 0-N-1、j=0-M-1ですべて成り立てば、内部にある。しかし、jは右辺にしかないし、クエリによらず一定。iを固定したときの最大値をO(NM)で求めておいて、すべてのクエリで使い回せる。左辺をクエリごとにN回計算すれば良いので、その処理はO(NQ)。N=50なので間に合う。反省。orange #式変形 2023-09-06
def prod(a, b):
return a[0]*b[1] - a[1]*b[0]
def plus(a, b):
return (a[0]+b[0], a[1]+b[1])
def minus(a, b):
return (a[0]-b[0], a[1]-b[1])
N = int(input())
P = [tuple(map(int, input().split())) for _ in range(N)]
P.append(P[0])
M = int(input())
V = [tuple(map(int, input().split())) for _ in range(M)]
maxprod = [-10**20]*N
for i in range(N):
diff = minus(P[i+1], P[i])
for j in range(M):
maxprod[i] = max(maxprod[i], prod(diff, plus(P[i], V[j])))
ans = []
Q = int(input())
for _ in range(Q):
a = tuple(map(int, input().split()))
for i in range(N):
diff = minus(P[i+1], P[i])
if prod(diff, a) < maxprod[i]:
ans.append('No')
break
else:
ans.append('Yes')
print(*ans, sep='\n')ABC250 G - Stonks
x ★ これは難問であり、学ぶことが多い。解説が非常にわかりやすい。実験し、規則に気づいて無証明で通す。というのが現実的。しかし実験をやり切る手数と、そこから規則性を見出す洞察力が両方必要。DPはまず、思いつくだろう。でも高速化する方法が検討つかない。そこで、書き出してみる。部分的に等差っぽく見える。(-> いや、等差なんて気づかねーよ!差に注目するのは基本なのかな?)差の数列を出力する。リストに追加された数字しかないと気づく!しかも単調増加してると気づく。そこに気づいた上で、最小値(つまりこの処理の流れで一番左の数字としてよい)とAiを比較して、 Aiの方が大きければ、左端を消してAiを2つ追加、Aiの方が小さければAiを追加(つまり左端になる)。という生成アルゴリズムを見出す。その上で、答えである、DP[0]はどう関係して動いてるか?Aiが大きい場合に「Ai - 左端の最小値」を足していくような動きをしていることを見出す。(ここがキツ!いや、全部きつい。) → この時点で規則性に確信を持てたら証明なしで提出だろう。解説に証明あるけど、コンテスト時間内に時間かけて考える意味はない。解説にグラフが凸で維持されると書いてあるが、これを考察しながら気づくのも至難の業。実験は不可避の問題だと思う。yellow #実験 2023-08-21
import heapq
N = int(input())
P = list(map(int, input().split()))
ans = 0
M = [P[0]]
for p in P[1:]:
if p > M[0]:
m = heapq.heappop(M)
ans += p - m
heapq.heappush(M, p)
heapq.heappush(M, p)
else:
heapq.heappush(M, p)
print(ans)改めてちゃんと理解。実験は大事だけど、この問題は実は意味で解けるべき問題だった。上記の実験から規則を見出すのは難しいかも。そういうアプローチを手として持っておくのは大事だけど。実際はこう考える。過去の安いときに買ったことにして売ればいい。すべてのタイミングで必ず売るとする。以前のタイミングで買っておく必要がある。これは一番安いときに買うことにする。以前の各タイミングでは2回まで買える。1回買えば売らなかったことに、2回買えば買ったことになる。毎回必ず売るとして処理できるのがムズいな。。。ムズいが、こういう別の問題に帰着すると、簡単になるのは醍醐味。もう少し厳密に説明すると、ある日の行動は、「買う」「何もしない」「売る」の3通りだが、この行動を1対1で言い換える。「買う」=「2回買って1回売る」、「何もしない」=「買って売る」、「売る」=「売る」。このように言い換えると、毎回必ず売ることにできる。毎回必ず売っているので、別の行動になってしまったように錯覚するが、1対1に対応付けられた変換なので、変わっていない。買う回数と売る回数も変わっておらず、この場合、最もお金が増えるのは、以前の安いタイミングで買えば良いのは明らかだ。そのため、それぞれのタイミングで2回まで買えるという条件のもと、もっとも安かった時に買えば良い。ポイントはやはり1対1の変換になっていること。 #1対1の変換 2024-05-02
// C++
using ll = long long;
using vll = vector<ll>;
#define rep(i,n) for(int i=0; i<n; i++)
int main()
{
int N;
cin >> N;
vector<ll> P(N);
rep(i, N) { cin >> P[i]; }
priority_queue<ll, vll, greater<ll>> buy;
ll ans = 0;
for (auto p : P) {
buy.push(p);
buy.push(p);
ans -= buy.top();
buy.pop();
ans += p; // sell
}
cout << ans << endl;
return 0;
}ABC250 F - One Fourth
o 良い。凸領域の面積は、x軸と2点に挟まれる領域の面積を一般的に求める関数を作ってぐるっと1周すれば計算できるんだなぁ。という事実を知った問題になった。自分で気づけてよかった。yellow 2023-07-04
def area2(p1, p2):
return (p1[1]+p2[1])*(p2[0]-p1[0])
N = int(input())
XY = [tuple(map(int, input().split())) for _ in range(N)]
XY = XY+XY
total = 0
for i in range(N):
total -= area2(XY[i], XY[i+1])
r = 1
rem = area2(XY[0], XY[1])
ans = 10**20
for l in range(N):
cur = area2(XY[l], XY[r]) - rem
ans = min(ans, abs(total - 4*cur))
while 4*cur < total:
r += 1
s = area2(XY[l], XY[r])
rem += area2(XY[r-1], XY[r])
cur = s - rem
ans = min(ans, abs(total - 4*cur))
rem -= area2(XY[l], XY[l+1])
print(ans)ABC249 G - Xor Cards
x ★ これはトップレベルで難しいと思った。K=0とかAが全部0とかのケースまで気が回せずに簡単にバグらせそうだし、赤Diffじゃないのがすごすぎる。条件分岐の整理が複雑で、方針に気づけても、コンテスト中にACできる気がしない。この問題を通じて、これまで気づいていなかったXOR掃き出しに関する学びも多かったし、何度か見直して良いと思う。XOR基底の結果で、線形従属の場合、0を追加しておく必要があると気づいた。というわけで、反省すべきは、ロジックを正確に整理する部分。紙に書いてみたけど、1枚埋まってしまってやっぱ複雑。ここに書こうかと思ったけどやっぱ面倒。#orange #XOR掃き出し #XOR基底 2023-09-07
def base(alist):
ret = []
zero = False
for a in alist:
for e in ret:
if a ^ e < a:
a ^= e
if a:
for i, e in enumerate(ret):
if a ^ e < e:
ret[i] ^= a
ret.append(a)
else:
zero = True
ret.sort(reverse=True)
if zero:
ret.append(0)
return ret
N, K = map(int, input().split())
pow2_30 = 2**30
ablist = []
for _ in range(N):
a, b = map(int, input().split())
ablist.append(a * pow2_30 + b)
abbase = base(ablist)
A = []
B = []
B0 = []
A1 = []
for i, e in enumerate(abbase):
a, b = e // pow2_30, e % pow2_30
if a == 0:
B0.append(b)
else:
A1.append(a)
A.append(a)
B.append(b)
ans = -1
if B0: # 0 must be le K
xor = 0
for e in B0:
if xor ^ e > xor:
xor ^= e
ans = xor
Kbits = []
Kcopy = K
while Kcopy:
s = Kcopy & -Kcopy
Kbits.append(s)
Kcopy -= s
Kbits.reverse()
i = 0
cura = curb = 0
selected = False
for Kbit in Kbits:
Kbit2 = Kbit * 2
while i < len(A1) and A1[i] >= Kbit2:
i += 1
if i == len(A1):
# pattern len(A1) == 0 was considered at first, see above
break
elif A1[i] & Kbit != 0:
# when no select A[i]
if i < len(A) - 1:
bb = base(B[i+1:])
xor = curb
for e in bb:
if xor ^ e > xor:
xor ^= e
ans = max(ans, xor)
cura ^= A[i]
curb ^= B[i]
selected = True
if cura <= K:
ans = max(ans, curb)
if B0:
xor = curb
for e in B0:
if xor ^ e > xor:
xor ^= e
ans = max(ans, xor)
i += 1
else: # A[i] & Kbit == 0
bb = base(B[i:])
xor = curb
for e in bb:
if xor ^ e > xor:
xor ^= e
ans = max(ans, xor)
break # finish
print(ans)ABC248 G - GCD cost on the tree
x ★ Twitterで検索して木DPと言ってる人が多いなぁと確認しても、くやしいが自力で構築できず。なんかムズいぞぉ~。なんで間に合うのかもいまいちピンときてない。何がムズいのかなぁ。根からつなぐとあるGCD値になるパス上の頂点数と、根からつなぐとあるGCD値になる端点数を覚えながら木DPと。うううううん。ムズい。なんだこれ。自然に出てこなかった。木をマージする時に新たに発生する個数の計算もトリッキーに見える。トリッキーに見えると同時になんか以前同じような処理やったような気もするという不思議な感覚。複数のトリックの合わせ技で思いつきにくくなっているということかもしれない。木1上の点と木2上の点をつなぐパスの場合に、増加するパス上の頂点数(つまりこの問題の答えに加算する値)は、木1上のパス上の頂点数x木2上の単点数。確かに木1上のパス上の頂点数は、木2上の単点数倍になるわ。逆も同じ。これで2つの木をマージしたときに答えに加算する値は求まる。その情報が必要だからこそ、DPでメモする値はそれらの値なのだ。気づきてぇ…。複雑そうではあるが、いざ実装し始めてみると意外と短いコードになるの、良いな。orange #GCD #木DP 2023-08-28
from collections import defaultdict
import math
M = 998244353
N = int(input())
A = list(map(int, input().split()))
G = [[] for _ in range(N)]
for _ in range(N-1):
u, v = map(int, input().split())
u, v = u-1, v-1
G[u].append(v)
G[v].append(u)
P = [-2]*N
P[0] = -1
S = [defaultdict(int) for _ in range(N)] # x: count of r-v points while gcd(r-v) == x
C = [defaultdict(int) for _ in range(N)] # x: count while gcd(r-v) == x
ans = [0]*N
stack = [~0, 0]
while stack:
cur = stack.pop()
if cur >= 0:
for nex in G[cur]:
if P[nex] == -2:
P[nex] = cur
stack.extend([~nex, nex])
else:
cur = ~cur
a = A[cur]
S[cur][a] += 1
C[cur][a] += 1
for nex in G[cur]:
if nex == P[cur]:
continue
ans[cur] = (ans[cur] + ans[nex]) % M
for y in C[nex]:
for x in C[cur]:
gcdxy = math.gcd(x, y)
ans[cur] = (ans[cur] + gcdxy * (C[cur][x]*S[nex][y] + C[nex][y]*S[cur][x])) % M
for y in C[nex]:
gcday = math.gcd(a, y)
C[cur][gcday] = (C[cur][gcday] + C[nex][y]) % M
S[cur][gcday] = (S[cur][gcday] + S[nex][y] + C[nex][y]) % M
print(ans[0])ABC247 G - Dream Team
x ★ この問題を解くために最小費用流を勉強する必要があり、理解するために丸1日費やした。蟻本を読んで少し読み進めるたびにわからんなーと思って寝っ転がって、頭の中で絵を描いて考えてわからんなーと。こんな時間の使い方はなかなかできない。帰省するつもりだったけど、台風7号が来ていて諦めた夏休みでもなければ。意地になって明け方まで考えてようやく納得できるところまでたどり着いた。蟻本ってやっぱむちゃくちゃ考えないと行間が埋まらないよなー。
最短経路(=最初コスト経路)を求めて、そこに限界まで流すということを、繰り返すと最小費用流が求まるという。最大流問題のアルゴリズムと同じで、流すと逆辺のキャパが発生して、今回はコストも逆になる。負の辺もあるので、ベルマンフォードで最短経路を求めるという。この時点で、え?負の閉路が発生したらどうするんだよと思うが、実は発生しない。X(複数辺でも良い)というコストに流すことによって負の閉路が発生するというのは逆辺-Xが発生して、それを含む負の閉路が発生するということ。しかし、図を書くとわかるように、負の閉路が発生するのであれば、XよりYの方が最短経路でなければならず、矛盾が起きる。よって最短経路に流しても負の閉路は発生しない。
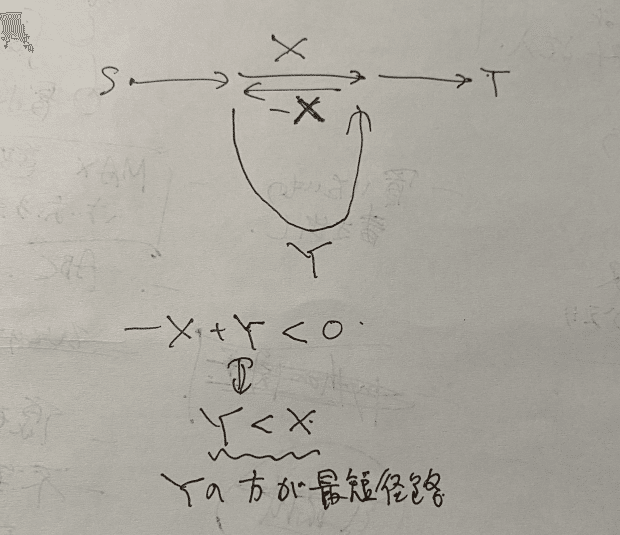
ではなぜこれで、最小費用が求まっているのか?最短路にフローを流したあとの状態で、常に最小費用を維持しているらしい。同じ流量でf'というフローの方がコストが小さいとする。f'-fというフローを考えると、全頂点において、入出流量の合計が0になる。なので、f'-fは複数の閉路で表される。(この部分は証明とかしてないけど感覚的には正しい。)f'の方がコストが小さいことから、必ず負の閉路が1つ以上存在しなければならない。しかし先程、負の閉路はできないことを確認した。よってこの手続きによって作ったフローは常に最小費用流となっている。しかしO(F|V||E|)と最悪計算量がでかすぎる。そこで、ポテンシャルという概念を導入して、ベルマンフォードではなくダイクストラを使って更新していけるようにする。ポテンシャルというのは、Sからその頂点までの最短経路のコストのこと。h(v)と表現する。そして、u->vを結ぶエッジeのコストd(e)をd'(e) = d(e) + h(u) - h(v)と変換すると、必ずd'(e) >= 0となる。なぜなら、h(u) + d(e) >= h(v)だから。(当然uを介してvに行くと最短経路以上のコストとなる。)ここで、d'とはなにか?と考えると、そのエッジを通ってvに行くと最短経路よりどれだけ遠回りか?ということを数値化したものであることがわかる。よって最短経路を通るエッジはすべてコストが0となり、最短経路ではない経路上のエッジが正のコストを持っている状態になる。負のコストの逆辺も含めて、d'はすべて0以上であり、ダイクストラ法を使える状態であることがわかる。最短経路にフローを流すと、グラフの構造が変化する。その状態でダイクストラ法で距離を計算する。結果のdistは何を表しているのか?そう、フローを流す前の最短距離からどれだけ距離が伸びたか?を表していることがわかる。フローを流して最短経路のエッジが使えなくなれば、その先の頂点へは、ダイクストラによって遠回りしたdistが求まるが、その値を現在のhに加えれば、新しい最短距離が求まるということで、考えると確かにそう。よって、ポテンシャルのhにダイクストラで求まったdistを加えてhを更新する。これで、フローを流したあとのポテンシャルの計算ができたことになる。これを流せなくなるまで繰り返すことで最小費用流を求めることができる。フローを流したあとの状態で、負の辺は発生していないのか?これは大事で、まず、最短経路のフローが通らないエッジは影響を受けず、コストは変わらず0以上のまま。流したことによって使い切って消えたエッジは考えなくて良い。逆辺が発生する場合、実は最短経路のフローが流れたエッジである時点で、d'(e)は0だったことがわかり、よってd'(rev(e))も0とわかる。d'(e) = d(e) + h(u) - h(v) = -(-d(e) + h(v) - h(u)) = -d'(rev(e)) = 0なので。よって、新しく 負の辺が発生することはなく、ダイクストラを適用することができる。ところですべての最短経路上で、ポテンシャルを考慮したd'は0。ダイクストラをやると、このd'=0の辺で最短経路ツリーが作られてたんだなぁと気づいた。(複数の最短経路もありうるのでd'=0を全部つなぐとツリーにならない可能性もあるが、1本選べばツリーを作れる。)そういうことに気づけたのも、最小費用流を長時間考えてたおかげだし、今後役に立つこともあるかもしれない。久しぶりに長時間考え続けた。最大流、Dinic法、強連結成分分解は大変だったけど、なんかそれらよりも大変だった気がする。FFTは同じくらい大変だったかも。理解してないSA-ISってのもある。yellow #最小費用流 2023-08-15
ABC246 G - Game on Tree 3
x これもムズい。どうしてそうなるの?って感じだった。最初にいくつ0にセットしておけば高橋くんにX以上を取られないか?でDP。その発想どっから出てくるんだよと。青木くんが1つずつ0にセットするゲームをすると言ってるのに、何個先にセットしておけばいいか?でDPする。なんでやねんと思ったんだけど、よく考えたら自分で考察してたときに、そういうことも考えていたことを思い出した。つまり、子孫の部分木の数字もまだ、そこまでたどり着いてないけど先回りして0に変えておかないといけないのではないか?と。そう考えると、「部分木ごとに先にいくつか0にしておく状態」がポイントとなることがわかる。ちゃんと考察した先にこの方針は成り立つのだ。まあ、激ムズだけど。二分探索の中で毎回親子関係を作り直してるので、それをやめて、処理順を先に確定させておけば、もう少し高速化できるはず。 yellow #DP #木DP #二分探索 2023-07-21
N = int(input())
A = [-1] + list(map(int, input().split())) # root=0 has no val
G = [[] for _ in range(N)]
for _ in range(N-1):
u, v = map(int, input().split())
G[u-1].append(v-1)
G[v-1].append(u-1)
def check(X): # check if T can get ge X
global N, A, G
stack = [~0, 0]
P = [-2]*N
P[0] = -1 # root's parent is -1
dp = [-1]*N # need to set 0 beforehand.
while stack:
cur = stack.pop()
if cur >= 0:
for nex in G[cur]:
if P[nex] == -2:
P[nex] = cur
stack.extend([~nex, nex])
else:
cur = ~cur
if len(G[cur]) == 1 and P[cur] != -1:
# leaf
dp[cur] = 1 if A[cur] >= X else 0
continue
temp = -1
for c in G[cur]:
if c == P[cur]:
continue
temp += dp[c]
temp = max(0, temp)
if A[cur] >= X:
temp += 1
dp[cur] = temp
return dp[0] > 0
l = 0
r = 10**9+1
while l + 1 < r:
m = (l + r) // 2
if check(m): # T can get m
l = m
else:
r = m
print(l)ABC245 G - Foreign Friends
x 黃Diffの問題連続でやってると自力で解けなくて自己肯定感下がるな。この問題をやってるときに、自分のダイクストラが、自分が理解しているダイクストラのロジックと違うということに気づいて直した。正しく動作はするけど、非効率な部分があるみたいな状態だった。まだそんな間違い残ってたのかぁ!気づけて良かったけど。有名人を起点とするダイクストラかなぁ、ってことは自分で思いついてたけど、そこから詰めきれなかった。ずばり、解説に書いてある「Sからある頂点までのパスとして短い方から3番目以降のものを含む経路がSから他の頂点へのパスとして2番目以内に入ってくることはない」って部分に気づけず、外国の有名人からの距離の処理を打ち切ったら、最短経路を求められない人が出てきてしまうんじゃないか?という疑問を払拭できなかった。残念!確かにその人を、2番目より大きなコストで通過して、別の人への距離が短くなるなんてことはありえない。同じところを2番目から進んだほうが確実に短くなるじゃんと…。これを気づけるかどうかなんだよなぁ。そういえばこの問題は、input高速化入れないとTLEx1だった。heapqにタプル入れるとAtCoderのPythonバージョンがkey対応してないから遅いんだよな。yellow #ダイクストラ 2023-07-20
import sys
input = sys.stdin.readline
import heapq
from collections import defaultdict
INF = 10**10
N, M, K, L = map(int, input().split())
A = [0] + list(map(int, input().split())) # 国
B = list(map(int, input().split())) # 有名人
edges = [[] for _ in range(N+1)]
for _ in range(M):
u, v, c = map(int, input().split())
edges[u].append((v, c))
edges[v].append((u, c))
costs = [defaultdict(lambda: INF) for _ in range(N+1)]
pq = []
for b in B:
pq.append((0, b, A[b]))
while pq:
cost, cur, fromc = heapq.heappop(pq)
if len(costs[cur]) >= 2 or fromc in costs[cur]:
continue
costs[cur][fromc] = cost
for nex, c in edges[cur]:
if len(costs[nex]) < 2:
heapq.heappush(pq, (cost + c, nex, fromc))
ans = []
for i in range(1, N+1):
for fromc in costs[i]:
if fromc != A[i]:
ans.append(costs[i][fromc])
break
else:
ans.append(-1)
print(*ans)ABC244 G - Construct Good Path
o ★ これでE、F、G、自力AC。そんなこと今まであったっけ?時間はかかったけど、自力ACは自信につながる。しかも、現在Python勢最速だ。うれしい。今、解説をすぐに見ずにねばる方針に変えようとしている。E、F、G、全部頂点を通る回数の偶奇性の話だったのに、全部解法を変えなければならないし、おもしろいなぁ。しかしなんで4N以下になるのか?わかってない状態で提出してしまった。最初の方針は、1点決めて1のところまで行って戻ってくるのをすべての1に対して繰り返すのかと思った。それで一応Sと一致させるアルゴリズムにはなっているので。しかし余裕で4N超えてしまい、考え直すことになり、気づけた。ところで結局のところ、なんで4N以下になるのか?ぼくの方法だと、デフォルトの通過回数は、末端が1、パス上で2、子をn持つ場合は、n+1か。Sに合わせることを調整と呼ぶと、子の調整の影響で+1、自分自身の調整の影響で+1、あれわからん、本当に4N以下になる?yellow #DFS 2023-09-27
この構築方法で4Nになる理由をちゃんと考えた。下の絵、左のようなグラフに対して、このアルゴリズムで経路を作っていくと、最悪のケースで右のようになる。最悪のケースでも4N以下にならなければならないので、最悪の場合、つまり、全頂点で調整のために1歩戻るということをくりかえした場合の経路を確認すべく、描いている。見ての通り、分岐している親ノードを4回以上通ることになる。しかも子要素が多ければ多いほどこの親ノードを通る回数は増えていく。そのせいで4Nに収まらないのではないか?という不安。しかし、この問題を通じておもしろい(当たり前でもある)事実があぶり出された。木って分岐するたびに末端ノードが1つ増えるよね。ということ。このことに気づけただけでも、この問題から大きな収穫だと思う。しかも末端ノードは最悪ケースで2回しか通らない。分岐のたびに分岐箇所を2回ずつ多く通ることになりそうだが、末端ノードが1つ増えるたびに2回余裕が生まれているので帳消しだ。よし、OK。 2023-09-28
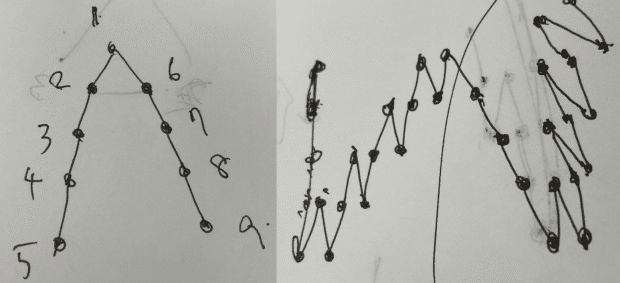
N, M = map(int, input().split())
G = [[] for _ in range(N)]
for _ in range(M):
u, v = map(int, input().split())
u, v = u-1, v-1
G[u].append(v)
G[v].append(u)
S = [int(c) for c in input()]
Snow = [0]*N # this must be S at last
C = [[] for _ in range(N)] # children
P = [-2]*N # parent
stack = [~0, 0]
P[0] = -1
ans = []
while stack:
cur = stack.pop()
if cur >= 0:
ans.append(cur+1)
Snow[cur] ^= 1
for nex in G[cur]:
if P[nex] == -2:
C[cur].append(nex)
stack.extend([~nex, nex])
P[nex] = cur
else:
cur = ~cur
if cur == 0: # this is the end
if Snow[cur] != S[cur]:
ans.pop()
else:
if Snow[cur] != S[cur]:
ans.extend([P[cur]+1, cur+1, P[cur]+1])
# needless to update Snow[cur]
else:
ans.append(P[cur]+1)
Snow[P[cur]] ^= 1
print(len(ans))
print(*ans)ABC244 F - Shortest Good Path
o ★ 時間かかったがひとまず自力AC。グラフ全体を1つの状態であり頂点とみなし、遷移を辺とした超グラフを作ってBFSで解く感じ。超グラフなんて言葉は聞いたこと無いがw。同じようなの見たことある。しかし、気づくのには時間がかかった。N = 17と小さく、17 x 2^17 = 2228224。状態数がこの数に収まる。制限時間4秒に対して3秒近くかかっている。Python勢の中でも遅め。でも考え方は解説そのもの。って思って、BFSの前にぼくが超グラフと呼んでいるものを作る必要ないなぁと思い、直接超頂点を計算しながら超グラフにおける距離を計算していったら、869秒で420くらいある提出の中で6位の速度になった。よかった。超グラフ作るのに定数倍、結構影響あったなぁ。事前に隣接グラフを作らなくても、頂点のidを逐次計算しながらBFSできる。大事。blue #bitDP #DP #超グラフ 2023-09-26
N, M = map(int, input().split())
pow2N = 2**N
G = [[] for _ in range(N)]
for _ in range(M):
u, v = map(int, input().split())
u, v = u-1, v-1
G[u].append(v)
G[v].append(u)
i2b = [1]
b2i = {1: 0}
for i in range(1, N):
nex = i2b[-1] * 2
i2b.append(nex)
b2i[nex] = i
H = [[] for _ in range(N*pow2N)] # at v, status is bit
for cur in range(N):
base = pow2N * cur
for bit in range(pow2N):
for nex in G[cur]:
H[base + bit].append(pow2N * nex + (bit ^ i2b[nex]))
from collections import deque
dist = [-1]*(N*pow2N)
q = deque([])
for v in range(N):
start = pow2N * v
q.append(start)
dist[start] = 0
while q:
cur = q.popleft()
for nex in H[cur]:
if dist[nex] == -1:
q.append(nex)
dist[nex] = dist[cur] + 1
ans = 0
INF = 10**15
for bit in range(pow2N):
temp = INF
for v in range(N):
temp = min(dist[pow2N * v + bit], temp)
ans += temp
print(ans)ABC244 E - King Bombee
o 寝る前に1問、って思ってやり始めたらムッズーと思ってしまった。これ、「DPじゃね?」案件だった。DPだと思うと簡単なのに、DPと気づかないと、激ムズ問題に見えてしまう。「DPじゃね?」は良い合言葉だと思ってるけど、定着はしてない。思い込みがないとも言えるけど。green #DP 2023-09-25
mod = 998244353
N, M, K, S, T, X = map(int, input().split())
G = [[] for _ in range(N+1)]
for _ in range(M):
u, v = map(int, input().split())
G[u].append(v)
G[v].append(u)
dpo = [0]*(N+1)
dpe = [0]*(N+1)
dpe[S] = 1
for i in range(1, K+1):
ndpo = [0]*(N+1)
ndpe = [0]*(N+1)
for v in range(1, N+1):
for nex in G[v]:
if nex == X:
ndpo[nex] = (ndpo[nex] + dpe[v]) % mod
ndpe[nex] = (ndpe[nex] + dpo[v]) % mod
else:
ndpe[nex] = (ndpe[nex] + dpe[v]) % mod
ndpo[nex] = (ndpo[nex] + dpo[v]) % mod
dpo = ndpo
dpe = ndpe
print(dpe[T])ABC243 G - Sqrt
o Fで苦労したが、同じ黄Diffでもこれはそこまで難しくなく、短時間で自力でACできた。Fが難しかったため、時間がなくてDiffが上がったのだろう。9x10^18を6回sqrtしたら1しか選べなくなってしまうので、最初の6回しか見なくていいことがわかる。パターン数を数えるってことでDPが適当だろうが、最初の項がデカすぎてそこからDPは書けない。3項目で55000くらいになるので、ここからはDPでいける。2項目は1項目のsqrtで範囲が確定、3項目のパターン数の初期値は、3項目の2乗より大きい数が2項目にいくつ含まれているか数えればいいから、55000回で計算できる。これでいけそうとわかる。yellow #DP #sqrt 2023-09-29
T = int(input())
def sqrt(a):
ret = int(a**0.5) + 1
while ret*ret > a:
ret -= 1
# ret*ret <= a
return ret
ans = []
for _ in range(T):
X = int(input())
Y = sqrt(X)
Z = sqrt(Y)
dp = [[0]*(Z+1) for _ in range(5)]
for i in range(1, Z+1):
dp[0][i] = Y - i*i + 1
for i in range(1, Z)[::-1]:
dp[0][i] += dp[0][i+1]
for i in range(1, 5):
for j in range(1, Z+1):
if j*j > Z or dp[i-1][j*j] == 0:
break
dp[i][j] = dp[i-1][j*j]
for j in range(1, Z)[::-1]:
dp[i][j] += dp[i][j+1]
ans.append(dp[4][1])
print(*ans, sep='\n')ABC243 F - Lottery
x ★ DPに持ち込む案件じゃね?とちょっと思ったけど、持ち込めず。包除原理か?M種類-M-1種類+…みたいな。しかしこれも式が導けない。これ包除原理できないんだぁ。って意外に思った。半分全列挙で半分ずつ計算してあとでまとめられないかな?、2^25 = 33554432はかなりでかいけど、、、とは思ったけどよく考えてみると、まとめられなかった。最近はできるだけねばる方針だけど、諦めて解説を見た。確率の式が出てくる。やられた感はあるが、すぐしっくりくるような内容ではない。この式変形によって、同じ商品をまとめることができて、商品を順番に処理するようなループが可能となる。各商品をci回当てる確率はK!xΠ(pi^ci/ci!)と式で表せる。これ、K個からc1,c2,c3,…,cN個ずつ選ぶコンビネーションってこんな式で表せるんだっけ?と驚いた。こんな表現が可能なら高校生の頃に数学で見たことがあるはずなのに、全然記憶がないのだ。なんかショック。計算すればわかることなんだけど。では、遷移はどうする?そんなにスッと出てくるようなものではないので、またショックを受ける。k回くじを引いて、m種類当たった確率を保持しながら、N個の商品をループする。pi^ci/ci!をかけながら。。。いや難しいよね。状態がO(KM)、遷移はO(K)、全部合わせて、O(NMK^2) = 50^4 = 6250000。それぞれの状態の確率を足していく。すごい不思議なDPだよなぁ。そして170ほどのPython勢の提出の中で、5番の速度で満足。yellow #DP #確率DP #確率 2023-09-29
mod = 998244353
N, M, K = map(int, input().split())
W = [int(input()) for _ in range(N)]
SW = sum(W)
invSW = pow(SW, mod-2, mod)
COUNT_MAX = K
fact = [0]*(COUNT_MAX+1)
invfact = [0]*(COUNT_MAX+1)
fact[0] = 1
for i in range(1, COUNT_MAX+1):
fact[i] = fact[i-1] * i % mod
invfact[COUNT_MAX] = pow(fact[COUNT_MAX], mod-2, mod)
for i in range(COUNT_MAX-1, 0, -1):
invfact[i] = invfact[i+1] * (i+1) % mod
invfact[0] = 1
dp = [[0]*(M+1) for _ in range(K+1)] # k回、m種類
dp[0][0] = 1
for w in W:
p = w * invSW % mod
powp = [1]
for i in range(1, K+1):
powp.append(powp[-1] * p % mod)
for k in range(1, K+1)[::-1]: # kがもらう
for c in range(1, k+1): # k-cから配る
pk = k - c # pkから配る
for m in range(M): # mから配る、m+1がもらう
dp[k][m+1] = (dp[k][m+1] + dp[pk][m] * powp[c] * invfact[c]) % mod
print(dp[K][M] * fact[K] % mod)ABC243 E - Edge Deletion
o ABC244 EFGに続き、順調に自力AC。結構難しいとは思うんだけど、いけるなぁ。最初全頂点からダイクストラ?って思った。ダイクストラでちょっと手間かければ最短経路出せるから。でもダイクストラの計算量はO((E+V) Log V)で、それに全頂点Vがかかる。EはV^2でV=300だから1億超えそう。その上、最短経路が複数あった時点でどっちもOKになってしまって消せるのか消せないのかわからなくなってしまう。破綻した。全点間距離ということでワーシャルフロイドが思い浮かぶ。これでいけないだろうか?いけるじゃんと気づく。辺の長さより最短距離が小さければ、間違いなく消せると判断できる。逆に辺の長さより最短距離が大きければ、間違いなく消せないと判断できる。おー1回のワーシャルフロイドで結構はっきり判断基準示されるじゃん!この気付き、割とムズいよね。で問題は辺の長さと最短距離が同じ時どうすんだ?と実装しながら気づいて、ウッとなる。しかしそこは少し悩むと、ワーシャルフロイドの結果から別頂点経由の最短距離は求められるから、全部調べればいいと気付ける。というわけで、ひとひねりを乗り越えるとで解けた。blue #ワーシャルフロイド 2023-09-28
INF = 10**15
N, M = map(int, input().split())
dist = [[INF]*N for _ in range(N)]
edges = []
for _ in range(M):
a, b, c = map(int, input().split())
a, b = a-1, b-1
edges.append((a, b, c))
dist[a][b] = c
dist[b][a] = c
for k in range(N):
for i in range(N):
for j in range(N):
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])
edges_ = []
ans = 0
for a, b, c in edges:
if c > dist[a][b]:
ans += 1
elif c == dist[a][b]:
for v in range(N):
if c == dist[a][v] + dist[v][b]:
ans += 1
break
print(ans)ABC242 G - Range Pairing Query
o Moのアルゴリズム。自力でいけた。最初test_08.txtだけTLEしてしまった。領域を√Q分割した結果、幅0が発生したのが原因。0のときは、1に調整すること。気をつけなければならない。#Moのアルゴリズム blue 2023-09-30
import bisect
N = int(input())
A = list(map(int, input().split()))
Q = int(input())
ndiv = int(Q**0.5) # 分割数
ends = []
w = wcopy = N // ndiv
if w == 0:
w = wcopy = 1
while wcopy <= N:
ends.append(wcopy-1)
wcopy += w
if ends[-1] != N-1:
ends.append(N-1)
qs = [[] for _ in range(len(ends))]
for i in range(Q):
l, r = map(int, input().split())
l, r = l-1, r-1
id = bisect.bisect_left(ends, l)
qs[id].append((l, r, i))
for i in range(len(qs)):
if i % 2 == 0:
qs[i].sort(key= lambda x: x[1])
else:
qs[i].sort(key= lambda x: -x[1])
colors = [0]*(N+1) # color is 1-N
curl = curr = 0
colors[A[0]] = 1
ans = [0]*Q
cur = 0
for i in range(len(qs)):
for l, r, q in qs[i]:
while curr < r:
curr += 1
colors[A[curr]] += 1
if colors[A[curr]] % 2 == 0:
cur += 1
while r < curr:
colors[A[curr]] -= 1
if colors[A[curr]] % 2 == 1:
cur -= 1
curr -= 1
while curl < l:
colors[A[curl]] -= 1
if colors[A[curl]] % 2 == 1:
cur -= 1
curl += 1
while l < curl:
curl -= 1
colors[A[curl]] += 1
if colors[A[curl]] % 2 == 0:
cur += 1
ans[q] = cur
print(*ans, sep='\n')ABC242 F - Black and White Rooks
o よし、ねばって自力AC。黃Diff。マス目の1辺N = 50。4重ループだからO(N^4) = 6250000のはず。NxMのマスに、黒い飛車B個と白い飛車W個をお互いに攻撃できないように配置する方法の数。問題がめっちゃ典型っぽい。典型っぽいのにすんなりいかない系。まず黒を置くことを考える。n行m列に配置すると、白は行列がかぶらないように、N-n行M-m列に配置する必要があり、その置き方はchooseで求まる。あとは、黒をn行m列を全部使って配置する方法の数を求める必要があることに気づく。この小問題がなお典型っぽい。が、どうやる?n行m列にB個置く方法はnm choose B、そこからnmより小さく、nmに含まれる領域の行列を全部使うパターン数を全部引けば、n行m列全部使う方法が数えられるとわかる。より小さい領域が先に求まっていれば良い、というのがDPっぽいので、DPでやる。ちゃんと考察すると、ちゃんと方針が見えてくる。chooseの第1引数<第2引数で渡してしまって、バグることが多い。関数の中でif文入れたほうがいいとは思うが。まあ気をつけるか。yellow #数え上げ 2023-10-11
N, M, B, W = map(int, input().split())
mod = 998244353
COUNT_MAX = N * M
fact = [0]*(COUNT_MAX+1)
invfact = [0]*(COUNT_MAX+1)
fact[0] = 1
for i in range(1, COUNT_MAX+1):
fact[i] = fact[i-1] * i % mod
invfact[COUNT_MAX] = pow(fact[COUNT_MAX], mod-2, mod)
for i in range(COUNT_MAX-1, 0, -1):
invfact[i] = invfact[i+1] * (i+1) % mod
invfact[0] = 1
def choose(n, r):
return fact[n] * invfact[r] * invfact[n-r] % mod
bptn = [[0]*(M+1) for _ in range(N+1)]
for n in range(1, N+1):
bptn[n][1] = 1 if n == B else 0
for m in range(2, M+1):
area = n * m
if area < B:
bptn[n][m] = 0
else:
cur = choose(area, B)
for n_ in range(1, n+1):
for m_ in range(1, m+1 if n_ < n else m):
cur = (cur - choose(n, n_) * choose(m, m_) * bptn[n_][m_]) % mod
bptn[n][m] = cur
ans = 0
for n in range(1, N+1):
for m in range(1, M+1):
if (N-n)*(M-m) >= W:
ans = (ans + choose(N, n) * choose(M, m) * bptn[n][m] * choose((N-n)*(M-m), W)) % mod
print(ans)★ これを包除原理でやるとはどういうことか?n行m列の中に配置する方法から、「1行か1列以上を含まないものを引く」と考える。「1行か1列以上含まないもの」を、包除原理で計算できるということ。なんか引く前の値も区別せずに計算できるからすぐ理解できなかったが。「引く部分」は、「1行か1列以上含まないもの全部の和」から、それらの2つ集合の積なので、「2行以上か1行1列か2列以上含まないものの和」を引き、3つの集合の積を足し、4つの…となるのか。計算量は上のDPの方法と同じ。 #包除原理 2023-10-11
ABC242 E - (∀x∀)
o 苦手。こういうのを短時間でやるのは重点課題。変にうまくやろうとしないのも大事だったりする。バグ入らせないわかりやすい実装優先。回文は半分で確定する。辞書順の「以下」は、初めて異なる文字になったときに小さいこと、一致している場合は文字列長が、「以上」であること。ていねいにやること。これがうまくやれてるかは不明。30分かかった。遅いだろう…。コンテスト中なら集中力でスピードアップするかな?light blue 2023-10-11
mod = 998244353
ORDA = ord('A')
pow26 = [0]*500005
pow26[0] = 1
for i in range(1, 500005):
pow26[i] = pow26[i-1] * 26 % mod
T = int(input())
ans = []
for _ in range(T):
N = int(input())
S = [ord(c)-ORDA for c in input()]
lenS = len(S)
even = True
Nhalf = N // 2
if N % 2 == 1:
even = False
Nhalf += 1
if lenS <= Nhalf:
cur = pow26[Nhalf-lenS]
for i in range(lenS):
cur = (cur + S[i] * pow26[Nhalf-i-1]) % mod
ans.append(cur)
else:
Xright = S[:Nhalf]
if not even:
Xright.pop()
X = S[:Nhalf] + list(reversed(Xright))
cur = 1 if X <= S else 0
for i in range(Nhalf):
cur = (cur + S[i] * pow26[Nhalf-i-1]) % mod
ans.append(cur)
print(*ans, sep='\n')ABC242 D - ABC Transform
o 30分かかっちまう。嫌な問題だけど文句言わずに速解き訓練せねば!解説は再帰関数?そっちのほうが良いかもしれないので要チェック★。ぼくは、60個なら下れるだろうと考えて、高さ60以下の3角形にして解いた。k-1を2進表記したものを上の桁から見て、1なら右へ、0なら左へという規則がわかったので、それに従って計算した。 light blue 2023-10-12
S = [ord(c)-ord('A') for c in input()]
Q = int(input())
ans = []
for _ in range(Q):
t, k = map(int, input().split())
k -= 1
if t <= 60:
onelen = 2**t
rep = k // onelen
amari = k % onelen
cur = S[rep] # top
bit = f'{amari:060b}'
for c in bit[-t:]:
if c == '1':
cur = (cur+2) % 3
else:
cur = (cur+1) % 3
ans.append(chr(ord('A')+cur))
else: # t > 60
cur = (S[0] + t - 60) % 3
for c in f'{k:060b}':
if c == '1':
cur = (cur+2) % 3
else:
cur = (cur+1) % 3
ans.append(chr(ord('A')+cur))
print(*ans, sep='\n')ABC241 G - Round Robin
x フローでは?と思ってどのようなグラフを作ればいいか考えてたが思いつかなかった。そのまま全頂点ペアがつながってるグラフに流すのか?という発想しか出てこず、できねぇなぁとなった。笑。なるほど、試合も頂点として、勝った方に流れるようにするのか。聞いてしまうと自然。燃やす埋める問題的にグリッドの行と列どちらか選ぶ、両方選ぶ、どちらも選ばないを表現する問題とかも見たことあって印象に残ったけど、この問題、閃かなかった。パズルだなぁ。i番目の人が残り全部勝った場合より1少ないキャパにしておく。それで最大流を流し、試合数と同じフローが流れれば、単独優勝の可能性があると言える。この手の問題で毎回グラフ作りなおすのは初めてだが、十分速い。実行時間204ms、Pythonで7位。そろそろこういう問題をコンテスト本番にACしたい!orange #最大流 2023-10-13
N, M = map(int, input().split())
nmatch = N * (N-1) // 2
win = [[0]*N for _ in range(N)]
nlose = [0]*N
match = [[0]*N for _ in range(N)]
m = N
for i in range(N-1):
for j in range(i+1, N):
match[i][j] = m
match[j][i] = m
m += 1
for _ in range(M):
w, l = map(int, input().split())
w, l = w-1, l-1
nlose[l] += 1
win[w][l] = 1
win[l][w] = -1
ans = []
S = N + nmatch
T = S + 1
for w in range(N):
nwin = N - 1 - nlose[w]
mf = MF(T + 1)
for m in range(N, N+nmatch):
mf.add_edge(S, m, 1)
for i in range(N):
if i == w:
mf.add_edge(i, T, nwin)
else:
mf.add_edge(i, T, nwin-1)
m = N
for i in range(N-1):
for j in range(i+1, N):
if win[i][j] == 1:
mf.add_edge(match[i][j], i, 1)
elif win[i][j] == -1:
mf.add_edge(match[i][j], j, 1)
else:
mf.add_edge(match[i][j], i, 1)
mf.add_edge(match[i][j], j, 1)
for i in range(N):
if i != w:
if win[w][i] == 0:
for e in mf.g[match[w][i]]:
if e[0] != w:
e[1] = 0
if mf.mf(S, T) == nmatch:
ans.append(w+1)
print(*ans)ABC241 F - Skate
o 止まる点が障害物の周囲1箇所なので、頂点の数は多くならない。グラフを作ってBFS。考え方は単純だ。しかし面倒。面倒なだけでDiffがずいぶん上がる。これを短時間で実装するのが競プロだが…。コツがなかなかつかめない。blue #BFS 2023-10-12
ABC241 E - Putting Candies
o 25分でAC、処理時間が93msでPythonベスト2だった。速解きを重要と意識し始めてるけど、25分かかった。本番ほど集中はできないけど、できるだけ速解きするよう心がける。シンプル実装でバグらないことを心がける感じ。効率的なコードって経験で身につくこともあるので、それはコンテストの中で身につけていく必要があるけども。周期解法だけど、ダブリングでもできると解説にある。どういうこと?★ light blue #周期 2023-10-12
import sys
N, K = map(int, input().split())
A = list(map(int, input().split()))
history = [0] # 0回目
nth_mod = [-1]*N
nth_mod[0] = 0
i = 0
s = s_ = 0
while True:
i += 1
cur = history[-1]
nex = cur + A[cur % N]
history.append(nex) # history[i] = nex
nex_mod = nex % N
if nth_mod[nex_mod] != -1:
s = nth_mod[nex_mod]
s_ = i
break
nth_mod[nex_mod] = i
if K <= s_:
print(history[K])
sys.exit()
loop = s_ - s
repeat = (K - s) // loop
amari = (K - s) % loop
print((history[s_] - history[s]) * repeat + history[s+amari])ABC240 G - Teleporting Takahashi
x ★ 全く計算量を落とす方法がわからず、解説を見たら驚くべきトリックを使っていた。z軸方向の移動回数を決めるループ、次にy軸方向の移動回数を決めるループ。この時点でN=10^7のところ、O(N^2)でアウトになってしまう。実はy軸方向の移動回数を決めるループが不要になるトリックがある。マンハッタン距離のテクニックで、45度回転というのがあるけど、なんと、あれを使う。x軸方向の移動はa(1, 0)、b(-1, 0)、y軸方向の移動はc(0, 1)、d(0, -1)でそれぞれに回数をふってからパターン数を計算しようとしていたが、割り振らずにまとめて計算できてしまう。右上に進むか左下に進むかでa、cか、b、dのどちらかが確定すると考える。さらに左上に進むか右下に進むかも決めると、完全に方向が確定する。(X, Y)まで進む移動を45度回転して(X+Y, X-Y)への移動と考えると、右上か左下か?と左上か右下かを同時に確定していってたどり着くか調べれば良いことがわかる。これで、x軸とy軸方向の移動に分けて考える必要がなくなった。常にななめにどっちに進むかを2つ同時に決める方法の数と考えられるので、ループは、z軸に移動をどれだけふるか?の1重で済んでしまう。やばい。orange #数え上げ #45度回転 2023-10-22
import sys
mod = 998244353
N, X, Y, Z = map(int, input().split())
COUNT_MAX = N
fact = [0]*(COUNT_MAX+1)
invfact = [0]*(COUNT_MAX+1)
fact[0] = 1
for i in range(1, COUNT_MAX+1):
fact[i] = fact[i-1] * i % mod
invfact[COUNT_MAX] = pow(fact[COUNT_MAX], mod-2, mod)
for i in range(COUNT_MAX-1, 0, -1):
invfact[i] = invfact[i+1] * (i+1) % mod
invfact[0] = 1
def choose(n, r):
return fact[n] * invfact[r] * invfact[n-r] % mod
X = abs(X)
Y = abs(Y)
Z = abs(Z)
left = N - X - Y - Z
if left < 0 or left % 2 == 1:
print(0)
sys.exit()
left //= 2
ans = 0
for z in range(left+1):
zshare = Z + 2*z
temp = choose(N, zshare) * choose(zshare, z) % mod
xyshare = N - zshare
U = X + Y
V = abs(X - Y)
ans = (ans + temp
* choose(xyshare, (xyshare - U) // 2)
* choose(xyshare, (xyshare - V) // 2)) % mod
print(ans)ABC240 F - Sum Sum Max
o Cの累積和がBということは、Cの値が同じうちはBはまっすぐに増えていったり、減っていったりする。Bの累積和がAということは、Aが最大値をとるタイミングは限られている。Bが負になる直前、もしくは一番最後かだ。しかしこういう問題もバグりやすいので、短時間でわかりやすく整理できるかが重要だなぁ。i==0とかi!=0という条件分岐のところが大事だったと記憶している。ところで、∣xi∣≤4っていう制約がなんで入ってるのか?理解できなかった。light blue 2023-10-13
T = int(input())
ans = []
for _ in range(T):
N, M = map(int, input().split())
ret = 0
A = 0
pB = 0
for i in range(N):
x, y = map(int, input().split())
if i == 0:
ret = x # init
nB = pB + x * y
if i != 0 and pB >= 0 and nB < 0: # x < 0
k = pB // -x
if k == 0:
ret = max(ret, A)
else:
tB = pB + x * k
tsum = (pB + x + tB) * k // 2
ret = max(ret, A + tsum)
rsum = (pB + x + nB) * y // 2
pB = nB
A += rsum
ret = max(ret, A)
ans.append(ret)
print(*ans, sep='\n')ABC240 E - Ranges on Tree
o 葉を見つけた順に数字を1から順にふっていく。帰りがけに、子要素の最小値と最大値ではさむように、L、Rを確定していけば、求めるL、Rの組をすべて確定できる。これ以上せまくするのは不可能。442msでPython実行時間順で1ページ目に出るの結構うれしい。green #木 2023-10-13
ABC239 G - Builder Takahashi
x ★これフローでしょ、と思って考えて、ひらめいて、ついにフローの問題自力でいけたか!と喜んだけど、最終的にACできなかった。なんと最小カットをちゃんと求めたことがなかった。これまで燃やす埋めるなどで、最小カットの問題を解いてきたつもりだったが、キャパが0になったところが必ず最小カットになっている問題ばかりだった。実はキャパ0=全部流れた辺=最小カットではない。全部流れている辺がつながっていて順番に流れているとき、最小カットは片方だ。つまりフローを流したあと、キャパが0であることを確認すれば良いのではなく、最小カットを求める処理が追加で必要だった。それが必要になったのが今回はじめてで、勉強になった。キャパが0出ない=まだ流せる頂点を全部見つけて、流せる頂点から流せなかった頂点への辺を、最小カットとする。初めてやった。yellow #最大流 #最小カット 2023-10-20
N, M = map(int, input().split())
mf = MF(2*N)
for _ in range(M):
a, b = map(int, input().split())
a, b = a-1, b-1
mf.add_edge(a, b+N, MF.INFFLOW)
mf.add_edge(b, a+N, MF.INFFLOW)
C = list(map(int, input().split()))
for v in range(1, N-1):
mf.add_edge(v+N, v, C[v])
print(mf.mf(0, 2*N-1))
gone = mf.go(0)
ans = []
for v in range(1, N-1):
if gone[v+N] and not gone[v]:
ans.append(v+1)
print(len(ans))
print(*ans)ABC239 F - Construct Highway
o 結構しんどかった。木構造において、N頂点でN-1辺で、次数の合計は2N-2となる。各頂点の次数が確定している時、木は作ることができるか?次数の合計が2N-2であることは条件。で、結論として、次数が0というものがなければ、具体的に作る方法を見つけたので、必ず木を作ることができることに気づけた。まず次数が2以上のものをパス状につなげる。で次数が余っているところに、次数が1だったものを順番につないでいく。これで作れるのだから、作れるということでOK。実際それをやるだけ。この問題は面倒だが。blue #木 2023-10-19
ABC239 E - Subtree K-th Max
o 部分木に含まれる頂点にかかれている番号のK番目を求める。K<=20なので、全頂点に20個もたせる余裕がある。帰りがけに子要素が持っている20個の数字を全部まとめ上げる必要があるが、変に大きい順に、などと考えず、全部マージしてソートして20個取れば良い。それが大した処理ではないことに気づく必要がある。green #木 2023-10-14
ABC238 G - Cubic?
x ★ Moでしょ、って思ってやったら最高でTLEx9で力尽きた。ダメらしい。Moのアルゴリズムの計算量は2N√Q、N=Q=200000を入れると178800000、ってあれ?この時点でNGかと思ったけど、MoのアルゴリズムでN=Q=200000ってのは過去にもあったので、3秒でもいける範囲なのだろう。しかし定数倍が重い。100万以下の数字の素因数は、2x3x5x7x11x13x17=510510なので、最大7つ。きついかな。実は100までの素数だけ累積和にしたらTLEx9だったんだけど。やっぱ無理があったのだろう。というより、想定解が天才すぎるトリックだったので、勉強になった。3回出てくると0に戻るようなハッシュ値を計算するというのだ。素数pに対して、2つの乱数a、bを生成する。素因数にpが1つ出てきたらハッシュ値にaをXORする、2つ目が出てきたらbをXORする、3つ目が出てきたらa^bをXORする。すると0になる。これをすべての素因数に対して行うと、ちょうどすべての素因数が3の倍数回出てきたタイミングでハッシュ値は0になる。よって、立方数であるかどうかを判定できる。トリッキーだ。4回で0になるものも乱数3つで作れるし。本当は立方数でないのに、ハッシュ値が0になってしまう確率は、この場合1/2^60になるらしい。なんで?つまりランダムに選んでいるからだろう。組み合わせで作れるパターン数を考えると0になる組み合わせは無数にあるから不思議ではあるが、毎回ランダムにするからこの確率になる。Qが200000であることを考慮して、決めれば良いと。2^20で乱数作ったら危ないのかな…。->ダメでした。WAx1。。。絶妙な感じだ。yellow #ハッシュ 2023-10-21
import random
MAXP = 1000000
P = [True]*MAXP
d = 2
while d*d < MAXP:
if not P[d]:
d += 1
continue
cur = 2 * d
while cur < MAXP:
P[cur] = False
cur += d
d += 1
rand = [[] for _ in range(MAXP)]
for p in range(MAXP):
if P[p]:
rand[p].append(random.randrange(2**60))
rand[p].append(random.randrange(2**60))
rand[p].append(rand[p][0]^rand[p][1])
def prime_factorization(n):
res = []
a = 2
while a*a <= n:
count = 0
while n % a == 0:
count += 1
n //= a
if count:
res.append((a,count))
a += 1
if n != 1:
res.append((n,1))
return res
N, Q = map(int, input().split())
A = list(map(int, input().split()))
pf = [[] for _ in range(1000001)]
now = [0]*MAXP # id of next random
_hash = [0]*(N+1)
for i, a in enumerate(A):
cur = i + 1
_hash[cur] = _hash[cur-1]
if not pf[a]:
pf[a] = prime_factorization(a)
for p, c in pf[a]:
for _ in range(c):
_hash[cur] ^= rand[p][now[p]]
now[p] = (now[p] + 1) % 3
for _ in range(Q):
l, r = map(int, input().split())
if _hash[l-1]^_hash[r] == 0:
print('Yes')
else:
print('No')ABC238 F - Two Exams
o ★ 最初、N=300なので、xが代表ならyも代表でなければならない条件を満たすペアをすべて決められるので、グラフを作ってそのグラフ内でk人選ぶ方法の数を事前計算->それを使ってグラフごとに確定していくDPか?と思ったけど、グラフ作ってもk人選ぶ方法の数を調べる方法がわからなかった。そこで、Pの方でソートしてからのDPでいけることに気づけた。Pの順位のうしろから順に選ぶか選ばないか確定していく。その時点で、Qの順位の最大値よりもQが小さい人は、必ず選ばなければならないとわかる。よって、選んだ人数とQの順位の最大値に対して、場合の数を記録していくDPをやればいい。yellow #DP 2023-10-20
mod = 998244353
N, K = map(int, input().split())
P = [p-1 for p in map(int, input().split())]
Q = [q-1 for q in map(int, input().split())]
p2q = [0]*N
for i, p in enumerate(P):
p2q[N-1-p] = Q[i] # p is descending
dp = [[[0]*N for _ in range(N)] for _ in range(K+1)] # select k fix p max Q [k][p][q]
dp[1][0][p2q[0]] = 1
for p in range(N-1):
np = p+1
nq = p2q[np]
# K and not select np
for q in range(nq):
dp[K][np][q] = (dp[K][np][q] + dp[K][p][q]) % mod
for k in range(1, K):
for q in range(nq):
dp[k][np][q] = (dp[k][np][q] + dp[k][p][q]) % mod # no select
dp[k+1][np][nq] = (dp[k+1][np][nq] + dp[k][p][q]) % mod # select
for q in range(nq+1, N): # must select
dp[k+1][np][q] = (dp[k+1][np][q] + dp[k][p][q]) % mod
dp[1][np][nq] = (dp[1][np][nq] + 1) % mod
print(sum(dp[K][N-1]) % mod)ABC238 E - Range Sums
o グラフを作って0からNにたどり着ければよいと気づけた。そこそこDiffが高そうなのはなぞ。light blue #グラフ #DFS 2023-10-19
ABC237 G - Range Sort Query
o 黃Diff、自力AC!昇順、降順してXがどこに行くか調べるには、X以外の数字は、Xより小さいか大きいかだけ見ればいいと気づけた!で小さい数字を全部1、X以上の数字を全部0として、遅延セグ木で区間和を管理する。[l,r]にいくつXより小さい数字が含まれているかさえ分かれば、昇順のときは、Xより小さい数字を前に集めて、全部1をセット、後ろに0をセット。降順のときはXより小さい数字を全部後ろに集めて、全部1をセット、前に0をセット。Xの位置は[l,r]に含まれているときだけ移動するし、移動先は0と1の境目なので、毎回動かしていくだけで良い。解説はなんか面倒なことしてた。これを期に遅延セグ木をちゃんと抽象化されたライブラリにしたいが、仕事で疲れすぎていて、とてもそんな余裕がない深夜。区間和の遅延セグ木、作るだけでもどうやるんだ?と思ってちょっと考えた。遅延セグ木を十分抽象化できていないのだ。下に伝搬するときは、1/2にして伝搬していけばいいなと。区間にセットするときは、セグ木を登るたびに2倍していけばいいなと。これをあーそれでいいなーと実装してAC!どうやって抽象化するの?っていうか一般的なライブラリは抽象化されてるから、やればできるはずなんだけども。yellow #遅延セグ木 2023-10-24
N, Q, X = map(int, input().split())
P = [0] + list(map(int, input().split()))
ix = 0
segt = SEGT_LAZY(N+1)
for i in range(1, N+1):
if P[i] < X: # Xより小さいものを1とする
segt.range_update(i, i+1, 1)
if P[i] == X:
ix = i # Xの位置は常に保持
for _ in range(Q):
c, l, r = map(int, input().split())
n = segt.query(l, r+1)
if c == 1:
segt.range_update(l, l+n, 1)
segt.range_update(l+n, r+1, 0)
if l <= ix <= r:
ix = l + n
if c == 2:
segt.range_update(l, r-n+1, 0)
segt.range_update(r-n+1, r+1, 1)
if l <= ix <= r:
ix = r - n
print(ix)ABC237 F - |LIS| = 3
o LISのアルゴリズムを競プロ始めて間もない頃見て、意味分からず、読むの諦めた記憶がある。そのときは、自力でセグ木を使ってLISを求める方法を編み出せたので、そっちのほうが簡単と思っていたけど、今あらためて読むとそうとしか思えないアルゴリズムだなぁ。と感慨深い。頭が変化しているよね。最初包除原理とかでできるのか?と思って考え始めたけど、全くできそうにないと気づいたので、ふとLISの解説を読んだら、あれ、理解できるぞとなり、この問題もそのアルゴリズムを使いながらDPやれば解けるぞ、となった。不思議だなぁ。セグ木を使わないLISは知ってないといけなかった。blue #LIS 2023-10-21
from collections import defaultdict
mod = 998244353
N, M = map(int, input().split())
dp = [defaultdict(int) for _ in range(N)]
for m in range(1, M+1):
dp[0][(m, 11, 11)] += 1
for i in range(1, N):
for p, c in dp[i-1].items():
for m in range(1, M+1):
if m > p[2]:
pass
elif m == p[2]:
dp[i][p] = (dp[i][p] + dp[i-1][p]) % mod
elif m > p[1]:
np = (*p[:2], m)
dp[i][np] = (dp[i][np] + dp[i-1][p]) % mod
elif m == p[1]:
dp[i][p] = (dp[i][p] + dp[i-1][p]) % mod
elif m > p[0]:
np = (p[0], m, p[2])
dp[i][np] = (dp[i][np] + dp[i-1][p]) % mod
elif m == p[0]:
dp[i][p] = (dp[i][p] + dp[i-1][p]) % mod
else: # m < p[0]
np = (m, *p[1:])
dp[i][np] = (dp[i][np] + dp[i-1][p]) % mod
print(sum([v for p, v in dp[N-1].items() if p[2] <= M]) % mod)ABC237 E - Skiing
x ★ 下り+H、上り-2Hとして、増えていくダイクストラをやれば解けるのではないかと思ったが、ダメらしい。どうもコンテスト本番で嘘ダイクストラで通した人が多かったらしく、after_contestのテストケースで落とされたっぽい。しかしなぜダメなのかよくわからない。負辺があるが、登るときのマイナスの方が大きいため、閉路を回ると必ず楽しさは小さくなり、絶対に更新されないので、収束すると思った。しかしダメだった。そして理由がわからない。このkyopro_friendsさんの説明らしいけど、見てもわからない。
フェネック「コンテスト中はダイクストラをする嘘解法が通ってたみたいだけど、こういうグラフのときにTLEになるよ。after_contestに追加したから嘘解法で通した子は解き直してねー」 pic.twitter.com/jTqrLc7odh
— 競技プログラミングをするフレンズ (@kyopro_friends) January 30, 2022
ダメなダイクストラの実装はこれ。after_contest_01と05で、TLEx2で、なんか永久に終わらないような挙動をしていた。
import heapq
INF = 10**15
N, M = map(int, input().split())
H = list(map(int, input().split()))
edges = [[] for _ in range(N)]
for _ in range(M):
a, b = map(int, input().split())
a, b = a-1, b-1
edges[a].append((b, H[a]-H[b] if H[a] > H[b] else 2*(H[a]-H[b])))
edges[b].append((a, H[b]-H[a] if H[b] > H[a] else 2*(H[b]-H[a])))
dists = [-INF]*(N)
pq = [(0, 0)]
ans = 0
while pq:
d, cur = heapq.heappop(pq)
d = -d
if d <= dists[cur]:
continue
dists[cur] = d # bigger the better
ans = max(ans, d)
for nex, c in edges[cur]:
if d + c > dists[nex]:
heapq.heappush(pq, (- d - c, nex))
print(ans)正しくは、ポテンシャルという概念を使って、負辺を除去してからダイクストラをするらしい。これは水の中でも簡単な方のDiffとはとても思えない。after_contest前の、コンテスト中の正解数で決めたDIffではないだろうか?下りの辺をすべて0とする。上りは高さ分のコスト。これでダイクストラをやって、最後に高さの差を加える。light blue #ダイクストラ #負辺除去 #ポテンシャル 2023-10-21
N, M = map(int, input().split())
H = list(map(int, input().split()))
edges = [[] for _ in range(N)]
for _ in range(M):
u, v = map(int, input().split())
u, v = u-1, v-1
if H[u] > H[v]:
edges[v].append((u, H[u]-H[v]))
edges[u].append((v, 0))
else:
edges[u].append((v, H[v]-H[u]))
edges[v].append((u, 0))
import heapq
INF = 10**15
dists = [INF]*(N)
pq = [(0, 0)]
ans = 0
while pq:
d, cur = heapq.heappop(pq)
if INF != dists[cur]:
continue
dists[cur] = d
ans = max(ans, H[0] - H[cur] - d)
for nex, c in edges[cur]:
if INF == dists[nex]:
heapq.heappush(pq, (d + c, nex))
print(ans)イマイチ納得できてなかった記憶があり、もう一度やってみる。できた。負辺があるとダイクストラは使えない。これは受け入れなければならない。で登るときが負辺なのでこれを消そう。負辺を消すときにポテンシャルという概念を持ち出すのはよくあること。登ると-2H減る。この重みを0にする。なので、下の方がポテンシャルが2H高いことにする。H登ればポテンシャルが2H減る。逆に下れば2H増える。しかし、下るときの楽しさは+Hだ。よって、辺の重みをHとする。ポテンシャルが2H増えるけどHのコストがかかるので、トータルで+Hとなる。今回楽しさを最大化するので、「ポテンシャルの増加 - 移動コスト」を最大化する必要があり、よって移動コストを最小化する問題に言い換えられた。これは問題を言い換えると解けるタイプの問題だ。そういう意味で、ABC250 G Stonksと似ていると感じる。速くはなってないけど、ちゃんと理解したのと、以前よりロジックがわかりやすいコード書くようになったかも。グラフ構築のところとか、ansの更新を最後にまとめたところとか。#言い換え 2024-05-02
import heapq
N, M = map(int, input().split())
H = list(map(int, input().split()))
edges = [[] for _ in range(N)]
for _ in range(M):
u, v = map(int, input().split())
u, v = u-1, v-1
edges[u].append((v, max(0, H[u]-H[v])))
edges[v].append((u, max(0, H[v]-H[u])))
INF = 10**16
dists = [INF]*(N)
pq = [(0, 0)]
while pq:
d, cur = heapq.heappop(pq)
if INF != dists[cur]:
continue
dists[cur] = d
for nex, c in edges[cur]:
if INF == dists[nex]:
heapq.heappush(pq, (d + c, nex))
ans = 0
for v in range(N):
ans = max(ans, 2*(H[0]-H[v]) - dists[v])
print(ans)ABC236 G - Good Vertices
x ★ 激ムズすぎた。最初にTLEになったコード。N bit整数つかって行き先を表現すれば、行列の積っぽい計算がO(N^2)でできたので、おっ、これはひらめいてしまったか?と期待したが、T=N^2ですべての時間においてグラフを更新して計算し直したので、トータル計算量はO(N^4 Log L)で、ダメだった。ワンチャンあるか?と思ったけど、N=100、L=10^9なので、はじめからノーチャンと思わなければならない。TLEx39でフィニッシュ。
import copy
N, T, L = map(int, input().split())
def double(a):
ret = [0]*N
for i in range(N):
frm = a[i]
cur = 0
to = 0
while frm:
if frm % 2 == 1:
cur |= a[to]
frm //= 2
to += 1
ret[i] = cur
return ret
def apply(a, v):
ret = 0
frm = 0
while v:
if v % 2 == 1:
ret |= a[frm]
v //= 2
frm += 1
return ret
ans = [-1]*N
step = [0]*N # [0] means go 2^0 [1] means go 2^1
for t in range(1, T+1):
u, v = map(int, input().split())
u, v = u-1, v-1
step[u] += 1 << v
go = copy.deepcopy(step)
l = L
cur = 1
while l:
if l % 2 == 1:
cur = apply(go, cur)
if cur == 0:
break
l //= 2
go = double(go)
to = 0
while cur:
if cur % 2 == 1:
if ans[to] == -1:
ans[to] = t
cur //= 2
to += 1
print(*ans)想定解法、473msでPython勢5位の速度。T=N^2で毎回計算するのではなく、辺のコストを追加時刻とし、そこにL回で到達する場合の通る辺のコストの最小値をDPするらしい。ちょっとトリッキーすぎる。。。最初の方法のように、T種類のグラフを作る必要はなく、1つのグラフ内にすべての情報がコストとして集約される。遷移でmaxのminを計算するのを、行列の積のように計算できるというのもかなりトリッキー。すごすぎる(T_T) orange #DP 2023-10-26
N, T, L = map(int, input().split())
INF = 100000
def double(a):
ret = [[INF]*N for _ in range(N)]
for i in range(N):
for j in range(N):
for k in range(N):
ret[i][j] = min(ret[i][j], max(a[i][k], a[k][j]))
return ret
def apply(a, v):
ret = [INF]*N
for i in range(N):
for j in range(N):
ret[i] = min(ret[i], max(a[j][i], v[j]))
return ret
W = [[INF]*N for _ in range(N)]
for t in range(1, T+1):
u, v = map(int, input().split())
u, v = u-1, v-1
W[u][v] = t
ans = [INF]*N
ans[0] = 0
while L:
if L % 2 == 1:
ans = apply(W, ans)
L //= 2
W = double(W)
print(*[(x if x != INF else -1) for x in ans])ABC236 F - Spices
o ★ 無証明AC。証明ムズいけど、読んでみると、これくらいはコンテスト中にここまで考えた上で提出したいものだと思った。値段でソートする。これまで選択したスパイスのXORで作れないものが出てきたら貪欲に選んでいく。なぜ貪欲でいいのか?スキップした方が安くなる可能性があるのではないか?すごく疑問。xがそれ以前のスパイスから作れないが、スキップするとする。するとxを作るのに、x以降のyが必ず必要になるので、x = (y, a, b, c)だったとする。XORの性質からy = (x, a, b, c)。任意のz = (a, b, c, …)について、yを含んでいる時、(x, a, b, c)で、置き換えてみよう。するとyの代わりにxを使ってすべてのzが作れることがわかり、何も考えずにxを選べばよかったことがわかる。XORの性質で同じものかけると消えるので、使ってたものを使わなくなるか、使ってないものを使うようになるか、なので、化かされたようだが、証明できた。これくらいならコンテスト中に証明できなければと思う。XORの問題よく出るし。まあ無証明で出すのも大事なテクニックではある。blue #XOR 2023-10-26
N = int(input())
C = [(i+1, c) for i, c in enumerate(list(map(int, input().split())))]
C.sort(key=lambda x: x[1])
base = []
ans = 0
for a, c in C:
for e in base:
if a ^ e < a:
a = a ^ e
if a:
ans += c
base.append(a)
if len(base) == N:
break
print(ans)ABC236 E - Average and Median
x ★ 典型といえる。平均を最大化する選び方と中央値を最大化する選び方。どちらも2分探索を使う。平均の方は食塩水の問題と同じ。水の量が個数なので、a-avgの値の和が0以上にできれば、平均をavg以上にできると考え、2分探索する。中央値。気づけなかった。悲しい。m以上の個数>m未満の個数にできれば、中央値はm以上にできると考える。blue #2分探索 #DP 2023-10-26
N = int(input())
A = list(map(int, input().split()))
l, r = 0, 10**9+1
while l + 0.00001 < r:
m = (l + r) / 2
dp1 = [0]*N # select
dp0 = [0]*N # not select
dp1[0] = A[0] - m
dp0[0] = 0
for i in range(1, N):
dp1[i] = max(dp1[i-1], dp0[i-1]) + A[i] - m
dp0[i] = dp1[i-1]
if max(dp1[N-1], dp0[N-1]) >= 0:
l = m
else:
r = m
print(l)
l, r = min(A), max(A)+1 # l l以上の方が多い r r以上の方が少ない
while l + 1 < r:
m = (l + r) // 2
# m以上 - m未満 の最大値
dp1 = [0]*N # select
dp0 = [0]*N # not select
dp1[0] = 1 if A[0] >= m else -1
dp0[0] = 0
for i in range(1, N):
dp1[i] = max(dp1[i-1], dp0[i-1]) + (1 if A[i] >= m else -1)
dp0[i] = dp1[i-1]
if max(dp1[N-1], dp0[N-1]) > 0:
l = m
else:
r = m
print(l)ABC235 G - Gardens
x ★やばすぎた。新しいトリックで勉強になった。n=0~N個からr個以下選ぶ方法の数をO(N)で計算できるらしい。最初どう計算するか全くわからず、組み合わせ苦手で厳しいなぁと思っていたが、グリッドという手法があるらしい。n<=rの場合は明らかに2^nだが、超えてくる場合にf(n) = 2xf(n-1) -n-1Crが成り立つと。n個から1つ選ぶ場合の数は、1回右、n-1回上に行く場合の数と考えられる。右に行く回数がr以下という条件になるので、右に行けない分を引いている。orange #グリッド #数え上げ 2023-10-26
mod = 998244353
N, A, B, C = map(int, input().split())
COUNT_MAX = N
fact = [0]*(COUNT_MAX+1)
invfact = [0]*(COUNT_MAX+1)
fact[0] = 1
for i in range(1, COUNT_MAX+1):
fact[i] = fact[i-1] * i % mod
invfact[COUNT_MAX] = pow(fact[COUNT_MAX], mod-2, mod)
for i in range(COUNT_MAX-1, 0, -1):
invfact[i] = invfact[i+1] * (i+1) % mod
invfact[0] = 1
def choose(n, r):
if n < r:
return 0
return fact[n] * invfact[r] * invfact[n-r] % mod
a, b, c = [0]*(N+1), [0]*(N+1), [0]*(N+1)
a[0] = b[0] = c[0] = 1
for i in range(1, N+1):
a[i] = (2 * a[i-1] - choose(i - 1, A)) % mod
b[i] = (2 * b[i-1] - choose(i - 1, B)) % mod
c[i] = (2 * c[i-1] - choose(i - 1, C)) % mod
ans = a[N] * b[N] * c[N] % mod
s = -1
for i in range(1, N+1):
ans = (ans + s * choose(N, i) * a[N-i] * b[N-i] * c[N-i]) % mod
s *= -1
print(ans)ABC235 F - Variety of Digits
o 桁DPだがしんどい。いろいろ罠があってACするまで苦労した。ロジックを考えている時点で、DPで個数を保持するのか、和を保持するのか迷った。で書いてるうちに、両方いるなと気づいて。両方DPした。そんなめんどうなの?と思ってしまってなかなかやる気でない。実装重い。そして、N以下の整数すべてなので、最上位桁まで確定しなくてもどんどん答えに加えていく必要がある。ことを最初忘れていた。yellow #桁DP 2023-10-27
ABC235 E - MST + 1
o クエリ先読みしてクラスカル法を実際にやる。green 2023-10-27
ABC234 G - Divide a Sequence
o 時間かかったが自力でいけた。159msでPython最速うれしい。dpをしながら、dp[i]への遷移は、dp[x]に[x+1, i]区間のmax-minをかけたものとわかる。しかし毎回max-minを計算しようとすると、計算量が、N=300000のところO(N^2)になってTLE不可避。iまで区間を伸ばしたときにmaxがどのように変化するか考える。maxの重要な性質、それを含むより長い区間のmaxは同じか、大きくなる。さらに新しいA[i]を区間に追加した時、maxが変化するのは、A[i]よりmaxが小さかった区間のみだ。よって、dp[i-1]とdp[i]は差分だけ更新して求めることができる。しかしややこしくて実装大変だった。yellow #スライド最大値 #DP 2023-10-28
mod = 998244353
N = int(input())
A = list(map(int, input().split()))
dp = [0]*(N+1)
dp[0] = 1
acm = [dp[0], dp[0] + dp[1]] # dpの累積和
max_ = [(0, A[0])] # (i, m) dpiからの追加分の最大値mがインデックスiまで続く
curmax = A[0]
min_ = [(0, A[0])]
curmin = A[0]
for i in range(2, N+1): # calc dp[i]
a = A[i-1]
prev = j = i - 1
while max_ and max_[-1][1] < a:
j, m = max_.pop()
curmax = (curmax - (acm[prev-1] - (acm[j-1] if j >= 1 else 0)) * m) % mod
prev = j
max_.append((j, a))
curmax = (curmax + (acm[i-1] - (acm[j-1] if j >= 1 else 0)) * a) % mod
prev = j = i - 1
while min_ and min_[-1][1] > a:
j, m = min_.pop()
curmin = (curmin - (acm[prev-1] - (acm[j-1] if j >= 1 else 0)) * m) % mod
prev = j
min_.append((j, a))
curmin = (curmin + (acm[i-1] - (acm[j-1] if j >= 1 else 0)) * a) % mod
dp[i] = (curmax - curmin) % mod
acm.append((acm[-1] + dp[i]) % mod)
print(dp[N])ABC234 F - Reordering
o いかにも典型感を醸し出してるが、残念ながら、ぼくはすぐに思いつかない。まず、各文字が何文字あるか?だけ意味があるとわかる。そこから文字を順番に何文字使うか?でDPする。いままで何文字使ったか?という状態がN=5000。遷移も文字数なのでN=5000。計算量はO(N^2)となる。次m文字使った時の挿入位置を前計算したchooseを使って求めれば良い。★畳み込みの方法が気になる。light blue #DP 2023-10-28
ORDA = ord('a')
count = [0]*26
for c in input():
count[ord(c) - ORDA] += 1
count.sort(reverse=True)
N = sum(count)
mod = 998244353
COUNT_MAX = N
fact = [0]*(COUNT_MAX+1)
invfact = [0]*(COUNT_MAX+1)
fact[0] = 1
for i in range(1, COUNT_MAX+1):
fact[i] = fact[i-1] * i % mod
invfact[COUNT_MAX] = pow(fact[COUNT_MAX], mod-2, mod)
for i in range(COUNT_MAX-1, 0, -1):
invfact[i] = invfact[i+1] * (i+1) % mod
invfact[0] = 1
def choose(n, r):
return fact[n] * invfact[r] * invfact[n-r] % mod
dp = [[0]*(N+1) for _ in range(26)]
for n in range(count[0] + 1):
dp[0][n] = 1
for i in range(1, 26):
for n in range(count[i] + 1):
for m in range(N+1):
if dp[i-1][m] > 0:
dp[i][n+m] = (dp[i][n+m] + dp[i-1][m] * choose(n+m, n)) % mod
print((sum(dp[25]) - 1) % mod)ABC234 E - Arithmetic Number
o 最近Pythonのyieldを使うとわかりやすく書けることがあるのではないかと思い始めてる。考察すると、最上位桁が同じか1つ上だけ調べればよいとわかる。なぜなら最上位桁が1つ上であれば、その値がaならaaaaが条件を満たすので。あと桁数も同じと考えて良い。9999が条件を必ず満たすので。よって、最上位桁が同じか1つ上の等差数をすべて返す関数を作って最初に「以上」になったものが答え。短時間で解答できるとよいが。green 2023-10-28
def create(x):
n = len(x)
tops = [x[0]]
if x[0] != 9:
tops.append(x[0] + 1)
for top in tops:
for d in range(-9, 10):
cur = top
ret = [cur]
for i in range(1, n):
cur += d
if 0 <= cur <= 9:
ret.append(cur)
else:
break
else:
yield(ret)
X = [int(c) for c in input()]
for a in create(X):
if a >= X:
print(''.join([str(i) for i in a]))
breakABC233 G - Strongest Takahashi
x ★ 2次元区間DPでしょと、そうとしか思えない感じの問題してて、その方針で考えても分からず。マジでつらい。自分に、「なんとかしろよ」と、言いたい。解説に、よく考えると、以下が成立することが分かります。と書いてある部分に気付けるか?がすべて。長方形区間に必要な体力は、少なくとも長い辺以下になるということまでは、考察できていたが、なんか長方形だし気持ち悪い。しかし、「もし長辺より小さい体力で破壊できるのであれば、長辺に空行か空列があってその両側に必要な体力の和が、長辺の長さより小さくなる」とわかれば見通しが良くなる。1箇所の空行だけ見ても最小値が見つからない場合があるので、分割する空行は連続する空行ごとに1つ調べる必要がある。空行全部に対して処理するとTLEだった。1つだけ処理するように変えて、ギリギリの1962ms。なかなか厳しい処理時間制限だ。DPのループを見ると計算量はO(N^5)。似たような問題を何度か見ても、まだ自力で遷移を導けない。orange #2次元区間DP 2023-10-28
N = int(input())
S = []
for _ in range(N):
S.append(list(input()))
dp = [[[[0]*(N+1) for h in range(N+1)] for j in range(N+1)] for i in range(N+1)]
for h in range(1, N+1):
for w in range(1, N+1):
for i in range(N+1-h):
for j in range(N+1-w):
if h == 1 and w == 1:
if S[i][j] == '#':
dp[i][j][h][w] = 1
elif h >= w:
dp[i][j][h][w] = h
pre = i-2
for i_ in range(i, i+h):
if dp[i_][j][1][w] == 0:
if i_ != pre + 1:
dp[i][j][h][w] = min(dp[i][j][h][w], dp[i][j][i_-i][w] + dp[i_+1][j][i+h-1-i_][w])
pre = i_
else: # h < w
dp[i][j][h][w] = w
pre = j-2
for j_ in range(j, j+w):
if dp[i][j_][h][1] == 0:
if j_ != pre + 1:
dp[i][j][h][w] = min(dp[i][j][h][w], dp[i][j][h][j_-j] + dp[i][j_+1][h][j+w-1-j_])
pre = j_
print(dp[0][0][N][N])ABC233 F - Swap and Sort
x ★ ムズいし、実装重い。なんか最近つらい(T_T) 自分の考察では、グラフ化して、葉ノードから順に確定していけば良いというものだった。そこまでは良い。が、移動パスを見つけるのに毎回DFSなどしていると、明らかに間に合わない。N=1000、M=200000でDFSは大体O(M)、それをN=1000回やることになるので。解説見たら最初に全域木作ってしまえば良いとのこと。確かに!連結成分内は木でつながるようになるし、その状態で葉ノードを順番に処理するアルゴリズムは有効だ。もう1つのトリックは、全域木内の移動パスを求めるのに、LCA(Lowest Common Ancestor)みたいな大げさなことをする必要はない。木になっている時点で、辺の数がNに落ちている。よってDFSのコストがもうO(N)なのだ。これに気づかず、LCAでやるぞ!と取り掛かっていると大幅な時間ロスとなる。ていうかやりたくもないし。気付けるかどうかが運命の分かれ道だ。難しいよなぁ。提出したら182msで、Python最速だったのはうれしい。yellow #全域木 #DFS 2023-10-28
import sys
N = int(input())
P = [0] + list(map(int, input().split()))
M = int(input())
G = [set() for _ in range(N+1)]
uf = Union(N+1)
edges = [[0]*(N+1) for _ in range(N+1)]
for i in range(M):
a, b = map(int, input().split())
if not uf.same_tree(a, b):
uf.unite(a, b)
G[a].add(b)
G[b].add(a)
edges[a][b] = i+1
edges[b][a] = i+1
leaves = []
for v in range(1, N+1):
if len(G[v]) == 1:
leaves.append(v)
ans = []
while leaves:
leaf = leaves.pop()
if P[leaf] != leaf:
stack = [~leaf, leaf]
used = [False]*(N+1)
used[leaf] = True
path = []
path_found = False
while stack:
cur = stack.pop()
if cur >= 0:
path.append(cur)
if P[cur] == leaf:
path_found = True
break
for nex in G[cur]:
if not used[nex]:
stack.extend([~nex, nex])
used[nex] = True
else:
path.pop()
if not path_found:
print(-1)
sys.exit()
while len(path) >= 2:
a, b = path[-2], path[-1]
ans.append(edges[a][b])
P[a], P[b] = P[b], P[a]
path.pop()
if G[leaf]: # last vertex is alone
nex = G[leaf].pop()
G[nex].remove(leaf)
if len(G[nex]) == 1:
leaves.append(nex)
for v in range(1, N+1):
if P[v] != v:
print(-1)
sys.exit()
print(len(ans))
print(*ans)ABC233 E - Σ[k=0..10^100]floor(X/10^k)
o 下の桁から順に確定していって、まとめて出力。10^500000は扱えないが、500000個の数字の和は5000000より小さいので、その程度なら扱える。green 2023-10-28
from itertools import accumulate
X = [int(c) for c in input()]
Xa = list(accumulate(X))
ans = [] # 下の桁から
left = 0
while Xa:
cur = Xa.pop() + left
ans.append(cur % 10)
left = cur // 10
if left != 0:
ans.append(left)
print(''.join([str(n) for n in reversed(ans)]))ABC232 G - Modulo Shortest Path
x ★ ひらめかず。解説すげーと思ったけど、賢い人なら経験なくても地頭だけで思いつきかねないような解法だったので、自分が閃けなかったことがくやしい。ダイクストラだよねと思って、愚直に無駄なのを除外していけば計算量が落ちるのかなとか思って考えてたけど、無理そうだったので、解説を見た。各頂点がA、Bの値を持っている時点で、なんか(A+B) mod Mをそのまま使うのではないのでは?と思ってもおかしくない。0からM-1までの頂点を作り、AをM-Aに変換して接続する。天才すぎる。たしかに条件を満たすグラフになる。0からM-1を頂点とするのかな?と少しでも問題から思えれば、思いつける可能性が出てくる。orange #mod #ダイクストラ 2023-10-30
import heapq
N, M = map(int, input().split())
A = []
B = []
nset = set()
for a in map(int, input().split()):
A.append(M-a)
nset.add(M-a)
for b in map(int, input().split()):
B.append(b)
nset.add(b)
nlist = sorted(nset)
n = len(nlist)
n2v = {n: N+i for i, n in enumerate(nlist)}
edges = [[] for _ in range(N+n)]
for v, t in enumerate(zip(A, B)):
a, b = t
edges[v].append((n2v[a], 0))
edges[n2v[b]].append(((v), 0))
for i in range(n-1):
edges[N+i].append((N+i+1, nlist[i+1] - nlist[i]))
edges[N+n-1].append((N, M + nlist[0] - nlist[n-1]))
INF = 10**16
dists = [INF]*(N+n)
pq = [(0, 0)]
while pq:
d, cur = heapq.heappop(pq)
if INF != dists[cur]:
continue
dists[cur] = d
for nex, c in edges[cur]:
if INF == dists[nex]:
heapq.heappush(pq, (d + c, nex))
print(dists[N-1])ABC232 F - Simple Operations on Sequence
x ★ 眠れない夜に。最初、置換操作数の合計はインデックスの差の半分という、無証明の根拠ない設定でぶっ込んだが、完全に間違いだった。半分くらいACしたが。置換回数は転倒数である。bitDPすると今までに確定したものが後ろに何個あるか?で置換回数を計算することができる。基礎的なことをちゃんと理解せねば。やばい。いい問題だなぁ。blue #bitDP #置換 #転倒数 2023-10-30
INF = 10**20
N, X, Y = map(int, input().split())
i2b = [1]
b2i = {1: 0}
for i in range(1, N):
nex = i2b[-1] * 2
i2b.append(nex)
b2i[nex] = i
A = list(map(int, input().split()))
B = list(map(int, input().split()))
dp = [INF]*(2**N)
dp[0] = 0
for bit in range(1, 2**N):
fix = bit.bit_count() # newly fixed
rev = fix - 1
a = A[fix - 1] # now watching
bcopy = bit
while bcopy:
new = bcopy & -bcopy
prev = bit - new
dp[bit] = min(dp[bit], dp[prev] + X * abs(B[b2i[new]] - a) + Y * rev)
bcopy -= new
rev -= 1
print(dp[2**N-1])ABC232 E - Rook Path
o 眠れない夜に。グリッドを4つの領域に分けると遷移が書けるので、DPする。light blue #DP 2023-10-30
mod = 998244353
H, W, K = map(int, input().split())
sx, sy, ex, ey = map(int, input().split())
dp = [[0]*4 for _ in range(K+1)]
if sx == ex and sy == ey:
dp[0][3] = 1
elif sx != ex and sy != ey:
dp[0][0] = 1
elif sx == ex:
dp[0][2] = 1
else:
dp[0][1] = 1
for i in range(K):
dp[i+1][0] = (dp[i][0] * (H+W-4) + dp[i][1] * (W-1) + dp[i][2] * (H-1)) % mod
dp[i+1][1] = (dp[i][0] + dp[i][1] * (H-2) + dp[i][3] * (H-1)) % mod
dp[i+1][2] = (dp[i][0] + dp[i][2] * (W-2) + dp[i][3] * (W-1)) % mod
dp[i+1][3] = (dp[i][1] + dp[i][2]) % mod
print(dp[K][3])ABC231 G - Balls in Boxes
x ★ 問題の内容からして積の和?と思ったけど、うまくいかず、何も思いつかず。積の和の復習できたのは良かったが。多分積の和でも解けるのだが…。ちょっとわからん。解説ACした。解説むずかしかった。いろいろな解説がされているので、研究すべきところ。そんなエネルギー今ないけど。この式変形、できないといけないなぁという感想。期待値の線形性とか基本対称式とかキーワード出てくる。i番目の箱にXi個追加で入れられるとすると以下を求めることになる。E ( Π ( Ai + Xi ) )。Πを展開すると、E ( Σ ( AのN-n次基本対称式 x Π (Aを選ばなかった残りn個) ( Xi ) )。Aの基本対称式は確定数値なので、EはXi n個の積の方だけにかかる。操作の対称性があるので、E Π Xiの値はどのn個を選んでも同じ。Sijでi番目の箱がj回目に選ばれたとするとXi = Σ Sij。j回目はどれか1つの箱にしかボールが入らないので、式を展開して考えると、Π Xiは、Sijが全部1になる場合の数と一致することがわかる。選び方がK x (K-1) x (K-2) x … x (K-n+1)でそれぞれのパターンの確率が(1/N)^nなので、掛け算してE Π Xiが求まる。n = 0~NでAのN-n次基本対象式の和 x E(n個) Π Xiを計算して足したものが答えとなる。実行時間が、Python最速の64msだったのうれしい。相変わらずまだまだ知らないこと出てきて橙しんどい。orange #数え上げ #基本対称式 #期待値 #式変形 #式展開 #期待値の線形性 2023-10-31
mod = 998244353
N, K = map(int, input().split())
A = [0] + list(map(int, input().split())) # 1 indexed
symsum = [[0]*(N+1) for i in range(N+1)] # Aiまでのk次基本対称式の和
symsum[1][0] = 1
symsum[1][1] = A[1]
for i in range(2, N+1):
symsum[i][0] = 1
for k in range(1, i+1):
symsum[i][k] = (symsum[i-1][k] + symsum[i-1][k-1] * A[i]) % mod
invN = pow(N, mod-2, mod)
xprod = [0]*(N+1)
xprod[0] = 1
xprod[1] = K * invN % mod
for i in range(2, N+1):
xprod[i] = xprod[i-1] * (K - i + 1) * invN % mod
ans = 0
for i in range(N+1):
ans = (ans + xprod[i] * symsum[N][N-i]) % mod
print(ans)ABC231 F - Jealous Two
o ちょっと悩んだが、かなり典型的な気がする問題。Aでソートする。小さい順にそれを高橋君にあげる場合の青木君へのプレゼントとしてありえる個数を足していけばいい。よって、セグ木に青木君へのプレゼントを追加していき、その時点で嬉しさが高橋君のプレゼント以上のものの数をセグ木から得れば良い。light blue #セグ木 2023-10-30
N = int(input())
A = list(map(int, input().split()))
B = list(map(int, input().split()))
blist = sorted(set(B))
segt = SEGT(len(blist))
b2c = {b: i for i, b in enumerate(blist)}
AB = list(zip(A, B))
AB.sort(key=lambda x: x[0])
i = 0
ans = 0
while i < N:
checkbs = []
a, b = AB[i]
checkbs.append(b2c[b])
segt.add(checkbs[-1], 1)
i += 1
while i < N and AB[i][0] == a:
_, b = AB[i]
checkbs.append(b2c[b])
segt.add(checkbs[-1], 1)
i += 1
for b in checkbs:
ans += segt.query(b, len(blist))
print(ans)ABC231 E - Minimal payments
o これが青DiffでFが水Diffってのがいまいちわからないけど、最初結構バグってイライラしたのでハマりやすいポイントがあるのかもしれない。大きい硬貨でよりXに近づけるのに、その何分の1かの硬貨を数回使って払う意味はないので、大きい順に使っていくということでOK。よく考えたらXに一番近い値は上と下に1つずつしかないので、i番目の硬貨の個数を決めた時点で上と下での最小数でDPすればよい。Xに一致すればその時点で最小値が答え。blue #DP 2023-10-30
ABC230 G - GCD Permutation
x ★ 激ムズ問題。かつ、聞いたことない新しいトリック来た。どうしても何も閃かないので解説を見ると、メビウス関数なるものが出てきた。この問題ではメビウス関数を変形したものを使用していた。pが奇数個の素数の積の時、u(p)=1、偶数個(0は含まない)の素数の積の時、u(p)=-1、それ以外(1か、同じ素数2つの積が入っている)時、u(p)=0とする。すると、(1以外の)nの約数dについて、u(d)の合計は、1となる。n=1のときは、0となる。なぜか?nの素因数がx個ある場合、そのうち1つを選ぶ方法は、xC1、これが、u(p)=1なので、xC1が足される。2つなら、xC2、引かれる。というように考えると、nの約数のdについて、u(d)の合計はxC1-xC2+xC3-…-(-1)^x xCxとなって、この値は、(1-1)^x=0より、xC0=1に等しくなる。これを使って、i, jのペアに対して、GCD(i, j)≠1かつGCD(Pi, Pj)≠1となるときに1、どちらかが互いにそのときに0となる式を作ることができる。iとjの共通の約数aとPiとPjの共通の約数bに対して、u(a)u(b)を合計すればよい。問題の条件を満たす時、aはGCD(i, j)の約数なので、GCD(i, j)>1であれば、先程書いた通り、u(a)の合計は1となる。同様にGCD(Pi, Pj)>1であれば、u(b)の合計は1となる。よって、u(a)u(b)は、u(a)の合計xu((b)の合計を展開したものなので、1となることがわかる。どちらかが互いに素であれば、u(1)=0なので、0になる。ここで、まさかの主客転倒。それぞれのu(a)u(b)が、すべてのi, jペアに対して計算したときに、何回使われるかを計算する。合計したものを計算すれば、条件を満たすペアの数が求まるというのだ。iがaの倍数でPiがbの倍数であるiの数が分かれば、その中でのi,jの組み合わせは、n(n+1)/2通りであることがわかるので、u(a)u(b)n(n+1)/2を加えれば良い、という具合に。u(a)≠0であるaに対して、aの倍数すべてに対し、Pの素因数をかけた値bを1回使うので、すべてカウントして計算する。このとき、N=200000なので、2⋅3⋅5⋅7⋅11⋅13⋅17=510510>200000より、それぞれ素因数は最大6個。その組み合わせは64通りしかないと、計算量を見積もることができる。すごい問題だった。メビウス関数の他の性質も調べて、使う問題解かないとなぁ。
この問題は難しすぎるので、N以下のi,jでGCD(i,j)≠1のものとか考えてみる。これでもちょっとむずかしい。2の倍数のペア+3の倍数のペア-6の倍数のペアみたいな約数包除原理になるので、よく考えたらこの+-がこの問題で出てきたu(a)の値であることがわかる。エラトステネスの篩的にこのu(a)を作れることが味噌。しかし、この問題と約数包除原理は全く似てるように見えないんだなwww応用したらできるって感じもしない。
関連問題としてABC304 Fを見直してたけど、なんか様相が異なるな。小さい順に約数を調べていって、初めて出てきたものだけカウントするために、引いてた。そういうパターンもあるな。ムッズ~。
何度も見てるw u(a)が出てくるのはiがaの倍数のときなので、N以下のaの倍数を列挙していく処理になる。これはエラトステネスの篩の計算量に従うので、O(N LogLogN)か。N=200000ならN LogLogNは800000程度と小さい。列挙したaの倍数axnに対して、Paxnの値を見て、これの素因数を列挙する(メビウス関数の計算時にすでに済)。素因数を1つずつ選んですべてのbを生成すれば、u(a)に対して、u(b9が出現するPがいくつあるか数えられる。u(a)u(b)の出現回数は2つ選んだ組み合わせなので、n * (n+1) / 2。何回見てもむずい。
orange #メビウス関数 #主客転倒 2023-11-02
from itertools import combinations
from collections import defaultdict
N = int(input())
P = [0] + list(map(int, input().split()))
pfs = [[] for _ in range(N+1)] # prime factors
prime = [True]*(N+1) # (only pfs maybe enough)
prime[0] = prime[1] = False
u = [-1]*(N+1) # odd p: 1, even p: -1, other: 0
u[0] = u[1] = 0
for p in range(2, N+1):
if not prime[p]:
continue
pfs[p].append(p)
u[p] *= -1
n = 2 # multiple
while True:
pxn = p * n
if pxn > N:
break
pfs[pxn].append(p)
prime[pxn] = False
u[pxn] *= -1
n += 1
tmp = p2 = p * p
while tmp <= N:
u[tmp] = 0
tmp += p2
ans = 0
for a in range(2, N+1):
ua = u[a]
if ua == 0:
continue
bcount = defaultdict(int)
axn = a
while axn <= N:
for r in range(1, len(pfs[P[axn]])+1):
for combi in combinations(pfs[P[axn]], r):
b = 1
for i in range(r):
b *= combi[i]
bcount[b] += 1
axn += a
for b, n in bcount.items():
ans += ua * u[b] * n * (n + 1) // 2
print(ans)ABC230 F - Predilection
x ★ 解けず。くやしい。別の区間を1つの数字にして同じ数列になる場合があるので、それを重複して数えないようにするにはどうするか?この点がこの問題の難しいところだが、別区間を加えて同じ数字になるのは、差の部分の和が0になるときである。よって、となんとかして引く回数をカウントしようとしていたが、ダメだった。答えは「操作手順で絞る」。なるほど一番最初にその数字になるときだけを新しい数列とみなすようにすれば、自動的に同じパターンをカウントしないようにできるのか。しかし最後まで来た場合だけは、全部カウントする。なんかややこしいdpになった。yellow #数え上げ #DP 2023-11-03
from itertools import accumulate
from collections import defaultdict
mod = 998244353
N = int(input())
A = list(map(int, input().split()))
Aacm = list(enumerate(accumulate(A)))
dacm = defaultdict(list)
acmsum = {}
for i, acm in Aacm:
dacm[acm].append(i)
for acm, ilist in dacm.items():
ilist.sort(reverse=True) # the last is the first
acmsum[acm] = 0
dp = [1]*N # 1 is itself
presum = 0
for i in range(N):
dp[i] = (dp[i] + presum) % mod
acm = Aacm[i][1]
dacm[acm].pop() # pop i
presum = (presum + dp[i]) % mod
acmsum[acm] = (acmsum[acm] + dp[i]) % mod
if dacm[acm]:
ni = dacm[acm][-1]
if ni != N-1:
dp[ni] = (dp[ni] - acmsum[acm]) % mod
print(dp[N-1])ABC230 E - Fraction Floor Sum
o iが小さいうちは1つずつ計算。同じfloor値が連続したところで、同じ数字がいくつ続くかを順番に計算していく方針に変更。何も証明せずAC。しかし1はコーナーケースとして入れていたものの、2もコーナーケースとしなければ通らない実装になっていて、REを出してしまった。気をつけねば。green 2023-10-31
import sys
N = int(input())
if N == 1:
print(1)
sys.exit()
if N == 2:
print(3)
sys.exit()
ans = pre = N // 1
i = 2
while True:
cur = N // i
if pre == cur:
break
ans += cur
pre = cur
i += 1
i -= 2
ans -= cur
while True:
if cur == 1:
ans += N - i
break
j = N // cur # curになる最後のインデックス
ans += (j - i) * cur
i = j
cur -= 1
print(ans)ABC229 G - Longest Y
o ★実装が重くて苦手だわ。1回でACできてホッとした感じの問題。n個並べられる時、個数がちょうど真ん中のところに集めるのが最適とわかるので、左側からと右側からの個数をnの半分に固定して、それぞれ移動回数を計算し、あとで結果をつきあわせて、K回以下のところがあれば、n個並べられると。i番目のYの位置を-iすることで、並べるのではなく、1箇所に集める問題にできるらしい。これはオモシロイと思った。yellow #2分探索 2023-11-03
S = list(input())
N = len(S)
Ys = []
for i, c in enumerate(S):
if c == 'Y':
Ys.append(i - len(Ys))
nY = len(Ys)
INF = 10**13
K = int(input())
l, r = 0, N+1 # l個並べられる、r個並べられない
while l + 1 < r:
m = (l + r) // 2
# ここで m == 0 はありえない
if m > nY: # impossible
r = m
continue
left = (m - 1) // 2 + 1
right = m - left + 1
countl = [INF]*nY
countr = [INF]*nY
i = 0
cur = 0
for j in range(left - 1):
cur += Ys[left - 1] - Ys[j]
countl[left - 1] = cur
for j in range(left, nY):
cur -= Ys[j-1] - Ys[i]
i += 1
cur += (Ys[j] - Ys[j-1]) * (left - 1)
countl[j] = cur
i = nY - 1
cur = 0
for j in range(nY - right + 1, nY):
cur += Ys[j] - Ys[nY - right]
countr[nY - right] = cur
for j in range(nY - right)[::-1]:
cur -= Ys[i] - Ys[j+1]
i -= 1
cur += (Ys[j+1] - Ys[j]) * (right - 1)
countr[j] = cur
cur = INF
for j in range(left - 1, nY - right + 1):
cur = min(cur, countl[j] + countr[j])
if cur <= K:
l = m
else:
r = m
print(l)ABC229 F - Make Bipartite
o ★ 難しい。頂点0を0グループとして1から順に0グループか1グループかのときの、削除辺重み総和の最小値をDPする。頂点1=N+1のところは、グループが一致している必要があるので2回DPする。最初頂点0からの辺を前回から何本目を残すか?みたいなことを考えてて複雑になってしまった。最大中2本消して、真ん中のBを削除するパターンがあり得るな。みたいな。方針ミスるとややこしくなってやばい。light blue #DP #2部グラフ 2023-11-03
INF = 10**15
N = int(input())
A = list(map(int, input().split()))
B = list(map(int, input().split()))
A.append(A[0])
dp = [[INF]*(N+1) for _ in range(2)] # N-1まで計算して最後帳尻を合わせる
dp[0][0] = 0
for i in range(1, N+1):
dp[0][i] = min(dp[1][i-1] + A[i], dp[0][i-1] + B[i-1] + A[i])
dp[1][i] = min(dp[1][i-1] + B[i-1], dp[0][i-1])
ans = dp[0][N]
dp = [[INF]*(N+1) for _ in range(2)]
dp[1][0] = 0
for i in range(1, N+1):
dp[0][i] = min(dp[1][i-1] + A[i], dp[0][i-1] + B[i-1] + A[i])
dp[1][i] = min(dp[1][i-1] + B[i-1], dp[0][i-1])
ans = min(ans, dp[1][N])
print(ans)ABC228 G - Digits on Grid
x ★ 激ムズ!これはいい問題。気づけたら天才的な数え上げだなぁ。かぶらないように数える。という問題は多い。最近だけでも2部グラフを数え上げるABC327 Gとか、ABC230 Fは操作をしぼることでかぶらないように数えられるということで、これはもしかしてこの問題に適用できない?とか思ったけど、無理だった。なんと、数字を確定して数えるのではなく、その数列を選んだあとで、あり得る行(または列)の集合でDPするというもの。問題の捉え方の転換がすごすぎる。すごすぎるし気づけないことも、同様の問題出て解ける自信など持てないことも、悔しすぎる。とりあえずPython最速の108msはうれしい。orange #数え上げ #DP 2023-11-09
from collections import defaultdict
mod = 998244353
i2b = [1]
b2i = {1: 0}
for i in range(1, 10):
nex = i2b[-1] * 2
i2b.append(nex)
b2i[nex] = i
H, W, N = map(int, input().split())
C = [[int(c) for c in input()] for _ in range(H)]
h2w = []
for i, cs in enumerate(C):
d = defaultdict(int)
for j, c in enumerate(cs):
d[c] += i2b[j]
h2w.append(d)
w2h = []
for j in range(W):
d = defaultdict(int)
for i in range(H):
d[C[i][j]] += i2b[i]
w2h.append(d)
h2w_ = [[] for _ in range(2**H)]
for bit in range(1, 2**H):
memo = [0]*10 # 1-9
bcopy = bit
while bcopy:
s = bcopy & -bcopy
for c, to in h2w[b2i[s]].items():
memo[c] |= to
bcopy -= s
for c in range(1, 10):
if memo[c] != 0:
h2w_[bit].append(memo[c])
w2h_ = [[] for _ in range(2**W)]
for bit in range(1, 2**W):
memo = [0]*10 # 1-9
bcopy = bit
while bcopy:
s = bcopy & -bcopy
for c, to in w2h[b2i[s]].items():
memo[c] |= to
bcopy -= s
for c in range(1, 10):
if memo[c] != 0:
w2h_[bit].append(memo[c])
dp = [[0]*(2**10) for _ in range(2*N+1)]
dp[0][2**H-1] = 1
for i in range(1, 2*N+1):
if i % 2 == 1:
for bit in range(1, 2**H):
if dp[i-1][bit] != 0:
for to in h2w_[bit]:
dp[i][to] = (dp[i][to] + dp[i-1][bit]) % mod
else:
for bit in range(1, 2**W):
if dp[i-1][bit] != 0:
for to in w2h_[bit]:
dp[i][to] = (dp[i][to] + dp[i-1][bit]) % mod
print(sum(dp[2*N]) % mod)ABC228 F - Stamp Game
o 自力でできたー。高橋君が選ぶ領域の中で、青木君は最大の領域を使うのだから、スライド最大値で青木君が選べる最大値を事前に求めておき、全領域で高橋君-青木君が最大になるものを答えれば良い。2次元累積和からの縦横2方向のスライド最大値ということで、実装重そうだったが、比較的短時間で1発でできてよかったと思う。しんどいので。Python3位の実行時間312msうれしい。yellow #スライド最大値 #2次元累積和 2023-11-09
from collections import deque
H, W, h1, w1, h2, w2 = map(int, input().split())
A = [list(map(int, input().split())) for _ in range(H)]
Aacu = [A[i][:] for i in range(H)]
for i in range(H):
for j in range(W-1):
Aacu[i][j+1] += Aacu[i][j]
for j in range(W):
for i in range(H-1):
Aacu[i+1][j] += Aacu[i][j]
hao = min(h1, h2)
wao = min(w1, w2)
aomax = [[0]*W for _ in range(H)]
for j in range(wao-1, W):
slide = deque([])
for i in range(hao-1, H):
pi, pj = i - hao, j - wao
cur = Aacu[i][j]
if pi >= 0:
cur -= Aacu[pi][j]
if pj >= 0:
cur -= Aacu[i][pj]
if pi >= 0:
cur += Aacu[pi][pj]
while slide and slide[0][0] < i - h1 + hao:
slide.popleft()
while slide and slide[-1][1] < cur:
slide.pop()
slide.append((i, cur))
aomax[i][j] = slide[0][1]
for i in range(hao-1, H):
slide = deque([])
for j in range(wao-1, W):
cur = aomax[i][j]
while slide and slide[0][0] < j - w1 + wao:
slide.popleft()
while slide and slide[-1][1] < cur:
slide.pop()
slide.append((j, cur))
aomax[i][j] = slide[0][1]
ans = 0
for i in range(h1-1, H):
for j in range(w1-1, W):
pi, pj = i - h1, j - w1
cur = Aacu[i][j]
if pi >= 0:
cur -= Aacu[pi][j]
if pj >= 0:
cur -= Aacu[i][pj]
if pi >= 0:
cur += Aacu[pi][pj]
ans = max(ans, cur - aomax[i][j])
print(ans)ABC228 E - Integer Sequence Fair
o ★ フェルマーの小定理。Mが割り切れるときは0と気づければ、modと互いに素な場合のフェルマーの小定理を使うことができ、解ける。light blue #フェルマーの小定理 2023-11-08
mod = 998244353
N, K, M = map(int, input().split())
if M % mod == 0:
print(0)
else:
print(pow(M, pow(K, N, mod-1), mod))ABC227 G - Divisors of Binomial Coefficient
x ★ 連戦連敗。疲れてる。約数の個数は、各素因数の個数が分かれば求まるという基本がある。それを前提として進めればいい。もしNがNより小さい素数で割り切れるなら、√N以下の素数で割り切れる。Nを√N以下の素数でNを割り切るもの全部で割って残るのは、素数。それが素数でないのなら、すでに割れているはずなので、割れてないから素数。つまりN=10^12なので、10^6までの素数で割っていけば、N-K+1からNまでの素因数は全部見つかる。ストレートにそれを実装する。yellow #約数 #素因数 2023-11-12
from collections import defaultdict
mod = 998244353
N, K = map(int, input().split())
nums = [k for k in range(1000001)]
p = 2
primes = []
count = defaultdict(int)
while p <= 1000000:
if nums[p] == 1:
p += 1
continue
# p is prime
primes.append(p)
cur = p
while cur <= 1000000:
while nums[cur] % p == 0:
nums[cur] //= p
if cur <= K:
count[p] -= 1
cur += p
p += 1
def n2i(n):
return n - N + K - 1
nums = [n for n in range(N-K+1, N+1)]
for p in primes:
if p * p > N:
break
n = ((N-K) // p + 1) * p
i = n2i(n)
while i < len(nums):
while nums[i] % p == 0:
nums[i] //= p
count[p] += 1
i += p
p += 1
for i in range(len(nums)):
if nums[i] != 1:
count[nums[i]] += 1
ans = 1
for _, n in count.items():
ans = ans * (n+1) % mod
print(ans)ABC227 F - Treasure Hunting
x ★ 連戦連敗。X以上の数のみをk回使った場合の最小コストでDPする。K回のものがあれば、それを採用。このXがHxW=30x30=900個しかないので、全部調べても間に合うという。すごすぎる。といいながら、こういうパターンは確かに見たことある。30^5=24300000。yellow #DP 2023-11-12
INF = 10**12
H, W, K = map(int, input().split())
A = []
nset = set()
for _ in range(H):
A.append(list(map(int, input().split())))
for a in A[-1]:
nset.add(a)
ans = INF
for X in sorted(nset):
dp = [[[INF]*(H+W) for _ in range(W)] for _ in range(H)]
for i in range(H):
for j in range(W):
a = A[i][j]
if i == j == 0:
if a >= X:
dp[i][j][1] = a
if a == X:
dp[i][j][0] = 0
else:
dp[i][j][0] = 0
continue
if i > 0:
for pk in range(i+j+1):
if a >= X:
dp[i][j][pk+1] = min(dp[i][j][pk+1], dp[i-1][j][pk] + a)
if a <= X:
dp[i][j][pk] = min(dp[i][j][pk], dp[i-1][j][pk])
if j > 0:
for pk in range(i+j+1):
if a >= X:
dp[i][j][pk+1] = min(dp[i][j][pk+1], dp[i][j-1][pk] + a)
if a <= X:
dp[i][j][pk] = min(dp[i][j][pk], dp[i][j-1][pk])
if dp[H-1][W-1][K] != INF:
ans = min(ans, dp[H-1][W-1][K])
print(ans)ABC227 E - Swap
x ★ 連戦連敗。さて、いつも全然できない数え上げだが。愚直に前から決めていく。そこまで思えたのは、価値あり。iまででEとYをe回、y回使って、遷移回数がkの場合の数でDPするらしい。なぜeとyをパラメーターとするのか?これが決まっていると、i番目の文字をK、E、Yにしたいときの移動距離(置換回数)が確定するからだ。その文字列を作るための最小回数で管理するから、数え上げが重複しない。yellow #DP 2023-11-12
S = [0 if c == 'K' else (1 if c == 'E' else 2) for c in input()]
N = len(S)
K = int(input())
movemax = N*(N-1)//2
dp = [[[[0]*(movemax+1) for _ in range(N+1)] for _ in range(N+1)] for _ in range(N)]
# iまで e文字 y文字 k=i+1-e-y文字 m move
ids = [N]*3
for i in range(N)[::-1]:
ids[S[i]] = i # 1番手前がセットされる
if ids[0] < N:
dp[0][0][0][ids[0]] = 1
if ids[1] < N:
dp[0][1][0][ids[1]] = 1
if ids[2] < N:
dp[0][0][1][ids[2]] = 1
mmax = 0 # move max previously
for i in range(1, N): # k, e, y <= i previously
pi = i - 1
mmax += N - i
for e in range(i + 1):
for y in range(i + 1):
for m in range(mmax + 1):
p = dp[pi][e][y][m]
if p > 0:
k = i - e - y
pre = [k, e, y]
count = [0]*3
ids = [-1]*3
mneed = 0 # i番目に持ってくるための必要な移動量
for j in range(N):
c = S[j]
count[c] += 1
if count[c] == pre[c] + 1:
ids[c] = mneed
if count[c] > pre[c]:
mneed += 1
if ids[0] != -1:
dp[i][e][y][m + ids[0]] += p
if ids[1] != -1:
dp[i][e+1][y][m + ids[1]] += p
if ids[2] != -1:
dp[i][e][y+1][m + ids[2]] += p
ans = 0
for e in range(N+1):
for y in range(N+1):
for m in range(min(movemax, K)+1):
ans += dp[N-1][e][y][m]
print(ans)ABC227 D - Project Planning
x ★この回は4問目で青DIff。参加してたら絶対崩れてる。ムズい。しかしいかにも典型っぽい内容の問題なので、有名なのかもしれない。問題見て、2分探索だろうなぁ、とは思うけど、mプロジェクト作れるか?短時間で判定できる方法が全く思いつかなかった。mより多い人数のグループをm人にして、全グループ合計した人数sumが、mK<=sumであれば、mプロジェクト作れる、mk>sumであれば、mプロジェクト作れない。と。聞いても一瞬なんでかわからん。作れないのは、まず理解できる。mプロジェクト作ろうとした時、m人以上のグループから全プロジェクトに1人ずつ使うのが最適であることは確かで、同じプロジェクトに同じグループから入れないので、m人からはみ出した人は、使えない。よって、mK>sumであればmプロジェクト作れない。確かに。まあこれに気づけた時点で勝ちだと思うけど、ムズいよなぁ。mK<=sumのとき必ずmグループ作れることも確認が難しい。1プロジェクト作るとK人減って残りの人数でm-1プロジェクト作れば良いので可能。ということだ。Python最速110msうれしい。blue #2分探索 2023-11-09
from itertools import accumulate
import bisect
N, K = map(int, input().split())
A = list(map(int, input().split()))
A.sort()
Aacu = list(accumulate(A))
l, r = 1, 10**18
while l + 1 < r:
m = (l + r) // 2
i = bisect.bisect_left(A, m)
cur = (Aacu[i-1] if i > 0 else 0) + m * (N - i)
if cur >= m * K:
l = m
else:
r = m
print(l)ABC226 G - The baggage
o 連戦連敗で落ち込む中、元気を取り戻したい黃Diff自力AC。おもしろい問題だった。こういうのがいいなぁ。知ってたらいけるみたいなのではなく、試行錯誤するやつ。1からと5から、確定的な部分をできるだけ潰していこうとしていた。たとえば、体力1の人は重さ1しか持てないので、限界まで使うなぁ。5の荷物は体力5の人しか持てないから持てなかったら終わりだなぁ。みたいな。上と下から攻めてるうちに、あれ?特定のAとBのペア同士の処理は貪欲でいくのが正解だなと気づいた。そして、正しい順序で処理していって最後にAが全部0になっているかどうかを確認すれば良いと、気づけた。で、処理は1つの関数にまとめて、順番に呼んだ。なんか想定解では整理して、手数がこれよりちょっと少ないかも。でもここまでいければ、まあいいと思う。yellow #貪欲 2023-11-14
T = int(input())
for _ in range(T):
A = [0] + list(map(int, input().split())) # 重さ
B = [0] + list(map(int, input().split())) # 体力
def consume(a, b):
n = b // a
r = b % a
blines = A[a] // n
if blines <= B[b]:
B[b] -= blines
if r > 0:
B[r] += blines
A[a] -= n * blines
if B[b] > 0 and A[a] > 0: # A[a] < n
B[b] -= 1
B[b - A[a] * a] += 1
A[a] = 0
else: # blines > B[b]
A[a] -= B[b] * n
if r > 0:
B[r] += B[b]
B[b] = 0
consume(5, 5)
consume(4, 4)
consume(4, 5) # B[1]
consume(1, 1)
consume(2, 2)
consume(1, 2) # B[1]
consume(3, 3)
consume(3, 5) # B[2]
consume(3, 4) # B[1]
consume(2, 2)
consume(2, 4) # B[2]
consume(2, 5) # B[1] B[3]
consume(2, 3) # B[1]
consume(3, 3)
consume(1, 1)
consume(1, 2)
consume(1, 3)
consume(1, 4)
consume(1, 5)
# print('A', A)
# print('B', B)
if A[1] == A[2] == A[3] == A[4] == A[5] == 0:
print('Yes')
else:
print('No')ABC226 F - Score of Permutations
x ★ 相変わらず連敗。非常に勉強になる数え上げ問題だった。まず、閉路の大きさの最小公倍数のK乗がスコアになることはわかる。よって閉路の数のパターンを数え上げる必要があるのだが、、、分割数という有名な問題らしい。その列挙の方法が想定解法に書いてなくて自力で実装。再帰関数使った。(なんでか知らんが同じことをDPでやったらやたら遅かった。)蟻本に載ってるらしいといううわさなので、確認したところ、載ってた。でも列挙方法ではなく、数え方しか書いてなかった。しかも激ムズ!理解に時間を要した。数え上げはこうするらしい。問題の制約のN=50を入れると204226通りとはじき出される。確かに十分少ない。かなりトリッキーなことをしていて、n個のボールをk個の箱に入れる方法として数えていく。なので、1以上の数に分割するのに、0(空箱)もできてしまうが、最終的にn個のボールをn個の箱に入れる方法は、1以上の数に分割する方法と一致する。いや、これがトリッキーすぎると思うんだが。相変わらず蟻本は、どれもこれも理解に時間がかかる。ちなみに、dp[n][k] = dp[n][k-1] + dp[n-k][k]、という遷移をする。左端が0個であれば、dp[n][k-1]、空箱がないならすべての箱から1つずつ除いて空箱ありの場合と一致するのでdp[n-k][k]。仮にこの遷移を自力でひねり出せたら怖いよ。みんなどういう感覚なんだろうか?
N = 50
dp = [[0]*(N+1) for _ in range(N+1)]
for k in range(1, N+1):
dp[0][k] = dp[1][k] = 1
for n in range(2, N+1):
dp[n][1] = 1 # always 1
for k in range(2, N+1):
dp[n][k] = dp[n][k-1] + (dp[n-k][k] if n-k >= 0 else 0)
print(dp[N][N])列挙は数え上げと全くことなるロジックで行った。n個をk個以下に分割する方法。左端の最大値fを決めると、残りはn-fをf以下に分割する方法なので、結合して作っていく。functoolsのcasheというデコレーターを使うと、同じ引数のときの戻り値をキャッシュしてくれるらしい。マジかよ。初めて知ったわ。分割数を列挙したら、長さLの閉路がF個あるという表現に変更し、その場合の数を求める。ここでも意外な事実が!場合の数は、N! Π(L,F) (L-1)^F / L!^F x F! なのだそうだ。(L-1)!が分母と分子で割り切れて気持ちいいのだが。実は分母の(L-1)^Fという部分は、自分で考察していたときに、同じ数字の組み合わせで閉路を作る方法は(L-1)^F通りあるなー、と考えていた。でもこの式全体は導けていなかった。気になるポイントは分母のF!だろう。2n個をn個とn個に分ける方法の数は、2nCn / 2 なのだった。このことを今まであまり意識したことがない。n-1個とn+1個に分ける方法の数は、2nCn-1で良い。なぜならn-1個のグループとn+1個のグループは区別できるから。どっちもn個だと同じパターンを2回数えてしまう。9個を3個と3個と3個に分ける場合の数は?そう、9C3 / 3! だ。同じパターンを6回数えてしまうから。なるほどねぇという感じ。20年も働いてるうちに数学力落ちて、こういうの、すぐピンとこないのがつらい。黃Diffの下くらいなので、みんなのレベルにビビる。yellow #分割数 #分割数列挙 #数え上げ 2023-11-14
import functools
import math
from collections import Counter
mod = 998244353
COUNT_MAX = 50
fact = [0]*(COUNT_MAX+1)
invfact = [0]*(COUNT_MAX+1)
fact[0] = 1
for i in range(1, COUNT_MAX+1):
fact[i] = fact[i-1] * i % mod
invfact[COUNT_MAX] = pow(fact[COUNT_MAX], mod-2, mod)
for i in range(COUNT_MAX-1, 0, -1):
invfact[i] = invfact[i+1] * (i+1) % mod
invfact[0] = 1
invpowlf = [[1]*51 for _ in range(51)] # l^f
for l in range(2, 51):
invl = pow(l, mod-2, mod)
for f in range(1, 51):
invpowlf[l][f] = invpowlf[l][f-1] * invl % mod
@functools.cache
def func(n, k):
'''split n with numbers le k'''
if k == 1:
return [[1]*n]
# k >= 2
ret = []
for f in range(1, min(n-1, k)+1):
for x in func(n-f, f):
ret.append([f] + x)
if n <= k:
ret.append([n])
return ret
N, K = map(int, input().split())
ans = 0
for x in func(N, N):
count = Counter(x)
score = pow(math.lcm(*count.keys()), K, mod)
ptn = fact[N]
for l, f in count.items():
ptn = ptn * invpowlf[l][f] * invfact[f] % mod
ans = (ans + score * ptn) % mod
print(ans)ABC225 G - X
x ★ 燃やす埋める。今度こそ、と粘ったが解けなかった上に、解説見てもいまいちピンとこない始末。いつになったら最初カットの燃やす埋めるの難しい問題を自力で解けるんだろう?このグラフの作り方だと、コストの最大値が2(H+W-1)C。線分を区切るだけでもっとコストが上がるのにって思ったけど、よく考えたらこれよりコストが小さくなるかを調べたいのだ。そう思ってもなおキモさ取れず。永久に苦手意識取れん。もう意味を理解しようとせず、虚無の世界でグラフを構築するような気持ちが必要なのだろうか?orange #最小カット #最大流 #燃やす埋める 2023-11-15
H, W, C = map(int, input().split())
A = [list(map(int, input().split())) for _ in range(H)]
S = H * W
T = S + 1
def idx(i, j):
return i * W + j
mf = MF(T+1)
for i in range(H):
base = i * W
for j in range(W):
mf.add_edge(S, base + j, A[i][j])
for i in range(1, H):
base = i * W
mf.add_edge(base, T, C)
mf.add_edge(base + W - 1, T, C)
for j in range(W):
mf.add_edge(j, T, C)
mf.add_edge(j, T, C)
for i in range(1, H):
base = i * W
for j in range(1, W):
mf.add_edge(base + j, base + j - W - 1, C)
for j in range(W-1):
mf.add_edge(base + j, base + j - W + 1, C)
ans = -mf.mf(S, T)
for x in A:
ans += sum(x)
print(ans)ABC225 F - String Cards
x ★ 難しい。この問題、辞書順で小さい->前から貪欲に考える。っていう単純な発想ではなく、気づけない。解説がすごい。DPでやるが、文字列を並べ替えて、i<jならば、Si+Sj<=Sj+Siが成り立っている状態にしてからDPする。DPする前になんらかの条件でソートするっていうのはEDPC Xがあったな。上記条件を満たすソートが可能である。文字列A、Bは26進数のa、bとみなせる。(文字列は26進数である。笑。)A+B<B+A ⇔ a26^|B|+b<b26^|A|+a ⇔ a/(26^|A|-1)<b/(26^|B|-1)という同値変形により、それぞれの文字列AとBのみに依存する数で並び替えられるからである。N-1からiまでの文字列で、k個使って作った文字列の最小でDPという単純なDPだが、こんな愚直に調べるDPなのが逆に盲点な気がする。先程のソートが役に立つ。ソートしない順序で作った方が小さくなることはあるか?ない。なぜなら、ソートした順序と逆の部分をスワップするだけで、より小さな文字列になるからである。いやーすごい。orange #DP #辞書順 2023-11-15
import functools
N, K = map(int, input().split())
S = [list(input()) for _ in range(N)]
def cmp(a, b):
ab = a + b
ba = b + a
if ab > ba:
return 1
elif ba > ab:
return -1
else:
return 0
S.sort(key=functools.cmp_to_key(cmp))
dp = [[[] for _ in range(K+1)] for _ in range(N)] # select k from i..(N-1)
dp[N-1][1] = S[N-1]
for i in range(N-1)[::-1]:
n = min(K, N - i)
for k in range(1, n+1):
dp[i][k] = S[i] + dp[i+1][k-1]
if dp[i+1][k]:
dp[i][k] = min(dp[i][k], dp[i+1][k])
print(''.join(dp[0][K]))ABC225 E - フ
x ★ 区間スケジューリング問題という典型問題らしい。これ自体は自明なアルゴリズム。区間が決まっている仕事をできるだけ数こなすには?終わりが早い順に見ていく。かぶらない最初のものを選ぶ。と。当たり前なのだが、ややこしく考えて、結局解説を見た。ぼくも自分の考察で、終わりが早い順で見ていたので、半分正解しかけていたのだが、x+yが大きいものと小さいもので、小さい方が原点に近いので、邪魔なので、もし区間がかぶっていたら、x+yが大きい方(遠い方)を優先する、とかややこしいこと考えていた。そうしたところ、半分以上WAとなってしまった。っていうか冷静になると、終わりが伸びてしまってもいいから原点から遠い方を優先するって、区間スケジューリングを理解した今となってはナンセンスなのだが。まあ勉強できてよかった。blue #区間スケジューリング問題 2023-11-15
import functools
N = int(input())
fs = []
for _ in range(N):
x, y = map(int, input().split())
fs.append(((x, y-1), (x-1, y)))
def cmp_ang(a, b):
ax, ay = a
bx, by = b
l = ay * bx
r = ax * by
if ax == 0 and bx != 0:
return 1
elif bx == 0 and ax != 0:
return -1
elif l > r:
return 1
elif l < r:
return -1
else:
return 0
def cmp(a, b):
return cmp_ang(a[1], b[1])
fs.sort(key=functools.cmp_to_key(cmp))
ans = [fs[0]]
for f in fs[1:]:
if cmp_ang(f[0], ans[-1][1]) >= 0:
ans.append(f)
print(len(ans))ABC224 G - Roll or Increment
o ★なんか最近連戦連敗で自信なくなってたけど、このABC224は、ある程度短い時間でDEFGを自力で解けた。確認したところ、ABC224はGまで解けば、100位以内だ。このGは、期待値を求める問題だが、数学寄りでおもしろく、これが普通に自力で解けたことはうれしい。高校生のころの数学力が20年以上の時を経て、徐々に戻ってきてるんだろうか?だとしたらうれしい。この期待値だが、1回サイコロを振った時点で、完全にランダムな状態になるので、サイコロを振る方が期待値が小さい出目の状態からの費用の期待値をeとすると、e = B + ΣEi / N とわかる。このeはサイコロを振る方が良い場合は、どの出目でも同じ値ということだ。サイコロを振らない方が良い場合はT以下の出目の状態で、Tに近い場合であることがわかる。振らないなら出目を1増やしながら毎回A払い続けるので、数字が小さいところから始めるほど、どんどんコストが増えて、最終的にeを超える。そこでサイコロを振った方が良いことになる。A払ったほうが良い下限をT-n+1とすると、先程の式は、B + ((N-n)e + n(n-1)A / 2) / N = e。さらに、A払ったほうが良いという条件から、(n-1)A <= e <= nA という不等式も導かれる。この2つの式から、n(n-1) <= 2NB/A <= n(n+1) という式が導かれた。もし、T-n+1が1未満である場合は1からT-1のときは、A払っていったほうが良い。総合すると、以下の短いプログラムが導かれた。yellow #期待値 2023-11-17
N, S, T, A, B = map(int, input().split())
NB2 = 2 * N * B
x = NB2 / A
n = max(1, int(x**0.5) - 1)
while NB2 > A * n * (n + 1):
n += 1
if T - n + 1 <= S <= T:
print(A * (T - S))
elif T - n < 0:
print(N * B / T + (T - 1) * A / 2)
else:
print(N * B / n + (n - 1) * A / 2)ABC224 F - Problem where +s Separate Digits
o 主客転倒で、それぞれの数字が、何桁目で何回使われるか?を数えて足す。こういうの自然にできるようになったのかな。後ろからのDPで、何桁目で何回というのを数え、前からは2の分割できる箇所数乗通り分割の仕方があるので、それをかける。blue #主客転倒 #DP 2023-11-17
mod = 998244353
S = [int(c) for c in input()]
N = len(S)
pow2 = [1]*(N+1)
for n in range(1, N+1):
pow2[n] = pow2[n-1] * 2 % mod
dp = [0]*N
dp[N-1] = 1
for i in range(N-1)[::-1]:
dp[i] = (dp[i+1] * 10 + pow2[max(0, N-2-i)]) % mod
ans = 0
for i, x in enumerate(S):
ans = (ans + x * pow2[i] * dp[i]) % mod
print(ans)ABC224 E - Integers on Grid
o いろいろと考えてておもしろい。同じ行か列にあるすべてのより大きな値に辺をはってしまうと、破綻するが、できるだけ移動回数を増やすので、次に大きな値にはっておけばいい。それより大きな値には経由して行った方が遠回りなので。よって辺の数をある程度抑えられるが、aの値が同じ頂点がたくさんあると?とちょっと不安になるも「移動先のマスに書かれている整数は、移動前のマスに書かれている整数より真に大きい。」という条件を見てホッとする。しかしそれだけではダメで、a=1が10万個、a=2が10万個同じ行にあると、1から2に全部辺をつなぐと破綻してしまう。よって、超頂点を使う必要がある。最初007.txtというテストケースでTLEを出してしまった。しかし、TLEになるのが1つだけに抑えられてるのがやらしいw DAG上の末端からのDPで最長距離を求めていくが、超頂点が邪魔をする。超頂点さえなければ、DAGの末端から遡るのは、この問題ではaの大きな順で良いはずだが、超頂点が追加されたことによって、自分でトポロジカルソート順を作ってやることになってしまった。親や出力次数などの管理が増えた。結果も超頂点がはさまってるので2で割る必要が生じた。 blue #超頂点 #DAGDP 2023-11-17
from collections import defaultdict, deque
H, W, N = map(int, input().split())
rs = defaultdict(list)
cs = defaultdict(list)
ais = []
for i in range(N):
r, c, a = map(int, input().split())
rs[r].append((a, i))
cs[c].append((a, i))
ais.append((a, i))
G = [[] for _ in range(N)]
vadd = N
for d in [rs, cs]:
for _, vs in d.items():
points = defaultdict(list)
for a, i in sorted(vs, key=lambda x: x[0]):
points[a].append(i)
points = list(points.items())
n = len(points)
for j in range(n-1):
for u in points[j][1]:
G[u].append(vadd)
G.append([])
for v in points[j+1][1]:
G[vadd].append(v)
vadd += 1
ans = [0]*vadd
leaves = deque([])
par = [[] for _ in range(vadd)]
deg = [0]*vadd
for v in range(vadd):
deg[v] = len(G[v])
if deg[v] == 0:
leaves.append(v)
else:
for nex in G[v]:
par[nex].append(v)
while leaves:
cur = leaves.popleft()
if not G[cur]:
ans[cur] = 0
else:
for nex in G[cur]:
ans[cur] = max(ans[cur], ans[nex])
ans[cur] += 1
for p in par[cur]:
deg[p] -= 1
if deg[p] == 0:
leaves.append(p)
print(*[a // 2 for a in ans[:N]], sep='\n')ABC224 D - 8 Puzzle on Graph
o グラフ全体の状態を1つの頂点と考えてグラフを作って、BFSで最小距離を求めると最小操作回数が求まるやつ。9! = 362880で、辺の数はその8倍。まあ十分小さい。light blue #超グラフ 2023-11-17
ABC223 G - Vertex Deletion
x ★ 一瞬最大マッチングは最小点カバーという事実から解けたかに思えたが、罠ありすぎて難しすぎた。木は2部グラフである。これもまあ意外とおもしろい事実。マッチングの親頂点を黒く塗るとする。子に白があれば貪欲に黒く塗ることで最大マッチングを作れることがわかる。しかしこの黒の塗り方は一意ではない。飛ばしても同じマッチング数を得られることはある。しかし別に全部書き出したいのではなく、この問題においては、ある頂点を消しても同じ最大マッチングか?である。貪欲に黒く塗ることで、根が白であれば、根を消しても最大マッチングが変わらないことを言える。なので、貪欲に塗らなければならない。さて、根以外はどうするのか?全方位木DPというものをする。つまり、親を子とみなして、その頂点が根であった場合の処理もやろうというのである。これがややこしすぎてハマりまくってストレスが半端なかった。マジで競プロ辞めたい。紙に場合分けをていねいに書き出して何時間もかかってACした。葉と根を特別扱いしなければならないところがやっかいすぎる!下からのDP、葉は白、子に白があれば黒、全部黒なら白だ。上からのDPは?その頂点に対し、親を子とみなしたときに何色か?調べる必要がある。そのために親の親と、兄弟の情報が必要。親の親と兄弟が全部黒なら親は白、親か兄弟に白がいれば、親は黒だ。しかし親が根の場合、親の親がいない。よって兄弟の情報のみ確認するが、兄弟がいない場合は親(根)は強制的に白となる。とはいえ、やっぱ一言で説明するなら、白がいたら黒、それ以外(葉か親の親も兄弟もいないパターン)は白、で足りるのかな?沼にハマると抜け出せない。Python勢2位の速度でうれしい。yellow #全方位木DP #木は2部グラフ #最大マッチング #木の最大マッチング 2023-11-18
N = int(input())
G = [[] for _ in range(N)]
for _ in range(N-1):
u, v = map(int, input().split())
u, v = u-1, v-1
G[u].append(v)
G[v].append(u)
P = [-2]*N
P[0] = -1
ans = [-1]*N # -1:not decided, 0:black, 1:white
color_below = [-1]*N
stack = [~0, 0]
while stack:
cur = stack.pop()
if cur >= 0:
for nex in G[cur]:
if P[nex] == -2:
stack.extend([~nex, nex])
P[nex] = cur
else:
cur = ~cur
if cur != 0 and len(G[cur]) == 1: # leaf
ans[cur] = color_below[cur] = 1
continue
for nex in G[cur]:
if nex != P[cur]:
if color_below[nex] == 1:
ans[cur] = color_below[cur] = 0
break # black child exist
else:
ans[cur] = color_below[cur] = 1
pcolor = [-1]*N # color of parent from above
stack = [0]
while stack:
cur = stack.pop()
for nex in G[cur]:
if P[nex] == cur:
stack.append(nex)
if cur == 0: # root
bro_count = len(G[0])
whilte_count = 0
for nex in G[cur]:
if P[nex] == cur:
# nex is a child
if color_below[nex] == 1:
whilte_count += 1
if bro_count == 1:
pcolor[G[cur][0]] = 1
else:
for nex in G[cur]:
if P[nex] == cur:
# nex is a child
if whilte_count - color_below[nex] > 0:
# brothers are all white
pcolor[nex] = 0
else:
pcolor[nex] = 1
else:
if pcolor[cur] == 1:
for nex in G[cur]:
if P[nex] == cur:
pcolor[nex] = 0
else: # pcolor[cur] is black
whilte_count = 0
for nex in G[cur]:
if P[nex] == cur:
# nex is a child
if color_below[nex] == 1:
whilte_count += 1
for nex in G[cur]:
if P[nex] == cur:
# nex is a child
if whilte_count - color_below[nex] == 0:
# brothers are all black
pcolor[nex] = 1
else:
pcolor[nex] = 0
for v in range(1, N):
if len(G[v]) == 1: # leaf
if pcolor[v] == 1:
ans[v] = 0
elif ans[v] == 1 and pcolor[v] == 1:
ans[v] = 0
print(sum(ans))ABC223 F - Parenthesis Checking
o なんかできたけど、すぐ思いつけるかな?という点で定着大事。(を+1、)を-1として累積和を取ると、正しい部分括弧列において、累積和aで始まり、累積和a-1で終わる。そして途中でa-1未満にならない。これが普通に気づけたのはなんか良いことだとは思うが、おそらく競プロ界隈では何も考えずに出てくる基礎のような気がする。(で始まっていなければならない。という条件を最初忘れていた。これ大事。ミスしたくねぇ。(が)になったり)が(になった場合、区間の累積和が-2になったり+2になったりするので、遅延セグ木で処理すれば良い。blue #遅延セグ木 #正しい括弧列 #累積和 2023-11-18
from itertools import accumulate
N, Q = map(int, input().split())
S = [1 if c == '(' else -1 for c in input()]
Sacu = list(accumulate(S))
segt = SEGT_LAZY(N, Sacu)
counter = 0
for _ in range(Q):
q, l, r = map(int, input().split())
l, r = l-1, r-1
if q == 1:
if S[l] == S[r]:
continue
segt.range_add(l, r, 2 * S[r])
S[l], S[r] = S[r], S[l]
else:
if S[l] == -1:
print('No')
continue
val = segt.query(r, r+1)
if val != segt.query(l, l+1) - 1:
print('No')
continue
if segt.query(l, r) < val:
print('No')
continue
print('Yes')ABC223 E - Placing Rectangles
o 全パターン調べる。なぜ水DIffかわからない。light blue 2023-11-18
ABC222 G - 222
x ★ オイラーの定理、aとnが互いに素なとき、a^φ(n) ≡ 1 (mod n)。ここでオイラーのファイ関数というものが出てくる。φ(n)は1からnまでの数のうち、nと互いに素な数の個数。こんなものが役に立つなんて。nと互いに素な数の集合Aを考える。Aの要素にそれぞれaをかけた集合Bを考える。Bの中身はmod nで異なる。同じものがあれば、引き算して、aとnは素なので、Aの要素の差が0とわかり、Bの同一の要素しかnで割った余りは同じにならないとわかる。よってAの積とBの積はmod nで等しい。Aの積は共通なので、割り算するとa^φ(n) ≡ 1 (mod n)が導かれる。解説の1行目にいきなり、22222=10^6-1みたいな言い換えが出てきて、その時点でやばっとなってしまった。数学のセンス失っててつらい。しかしPythonの提出の中で最速89ms、2位100ms!うれしい。yellow #オイラーのφ関数 #オイラーの定理 #整数論 2023-11-29
def phi(n):
res = n
a = 2
while a * a <= n:
count = 0
while n % a == 0:
count += 1
n //= a
if count:
res -= res // a
a += 1
if n != 1:
res -= res // n
return res
def divisors(n):
l, u = [], []
a = 1
while a * a <= n:
if n % a == 0:
l.append(a)
u.append(n // a)
a += 1
if l[-1] == u[-1]:
u.pop()
return l + u[::-1]
T = int(input())
ans = []
for _ in range(T):
K = int(input())
if K == 1:
ans.append(1)
continue
d2 = 0
while K % 2 == 0:
K //= 2
d2 += 1
if d2 > 1 or K % 5 == 0:
ans.append(-1)
continue
K *= 9
for d in divisors(phi(K)):
if pow(10, d, K) == 1:
ans.append(d)
break
print(*ans, sep='\n')x ★ baby-step giant-stepでも解ける。忘れててわけがわからないことになった。baby-stepを先にやっておいて、giant-stepを小さい順に調べて、合致したら答え。giant-stepの方が大股なんだから効くので、当たり前だった。これって平方分割なんだよなぁ。そのことを頭に叩き込まないと。Mo's algorithmに似てるとすら思えるし。10^n≡1 (mod K) なる最小のnを求める問題。m = ceil(n**0.5)とし、n=im+jとして調べる。10^im≡10^-j (mod K)。nは1以上なので、jを1からmまでbaby-stepする。その後、iを0からm-1までgiant-stepする。離散対数問題忘れるな!yellow #babystepgiantstep #離散対数問題 #平方分割 2023-11-29
import math
T = int(input())
ans = []
for _ in range(T):
K = int(input())
if K == 1:
ans.append(1)
continue
d2 = 0
while K % 2 == 0:
K //= 2
d2 += 1
if d2 > 1 or K % 5 == 0:
ans.append(-1)
continue
K *= 9
m = math.ceil(K**0.5)
bs = {} # baby step
cur = 1
inv10 = pow(10, -1, K)
for j in range(1, m + 1):
cur = cur * inv10 % K
if cur not in bs:
bs[cur] = j
cur = 1
pow10m = pow(10, m, K)
for i in range(m):
if cur in bs:
ans.append(i * m + bs[cur])
break
cur = cur * pow10m % K
else:
ans.append(-1)
print(*ans, sep='\n')ABC222 F - Expensive Expense
x ★木の直径の性質。どの頂点からも、最長経路の頂点は直径の両端のどちらかとなる。これ知らなかった。この性質がこの問題そのもの。木の直径を自力で導いたころの忍耐なら気づけたかも?などと、粘りがなくなってないかと心配になる。直径の候補が複数あっても、距離が知りたいだけだし、同じ距離なので、気にしなくていい。blue #木の直径 2023-11-29
N = int(input())
G = [[] for _ in range(2*N)]
for _ in range(N-1):
a, b, c = map(int, input().split())
a, b = a-1, b-1
G[a].append((b, c))
G[b].append((a, c))
for v, d in enumerate(map(int, input().split())):
v_ = v + N
G[v].append((v_, d))
G[v_].append((v, d))
dist = [-1]*(2*N)
dist[0] = 0
stack = [0]
S = 0
maxd = 0
while stack:
cur = stack.pop()
for nex, d in G[cur]:
if dist[nex] == -1:
dist[nex] = dist[cur] + d
stack.append(nex)
if dist[nex] > maxd:
maxd = dist[nex]
S = nex
dist = [-1]*(2*N)
dist[S] = 0
stack = [S]
T = 0
maxd = 0
while stack:
cur = stack.pop()
for nex, d in G[cur]:
if dist[nex] == -1:
dist[nex] = dist[cur] + d
stack.append(nex)
if dist[nex] > maxd:
maxd = dist[nex]
T = nex
dist_ = [-1]*(2*N)
dist_[T] = 0
stack = [T]
while stack:
cur = stack.pop()
for nex, d in G[cur]:
if dist_[nex] == -1:
dist_[nex] = dist_[cur] + d
stack.append(nex)
for v in range(N):
if S == v + N:
print(dist_[v])
elif T == v + N:
print(dist[v])
else:
print(max(dist[v], dist_[v]))o ★ 別解。っていうか普通に考えたら全方位木DPになると思うし、全方位木は実装しんどいけど、書けなきゃと思う。とりあえず一発でいけてよかった。累積MAX的な処理が必要。そういえば累積積とか、全方位木DPで出てきがち。解説には全方位木DPを抽象化してライブラリでというようなコメントもあった。なんか全方位木DPライブラリ化したいみたいなコメントをTwitterでもいくつか見た。が、いまいち抽象化しづらい。毎回雰囲気が違う気がする。Python提出の中で速めなのうれしい。blue #累積MAX #全方位木DP 2023-11-29
N = int(input())
G = [[] for _ in range(N)]
for _ in range(N-1):
a, b, c = map(int, input().split())
a, b = a-1, b-1
G[a].append((b, c))
G[b].append((a, c))
D = list(map(int, input().split()))
P = [-2]*N
P[0] = -1
stack = [~0, 0]
maxbelow = [0]*N
while stack:
cur = stack.pop()
if cur >= 0:
for nex, c in G[cur]:
if P[nex] == -2:
stack.extend([~nex, nex])
P[nex] = cur
else:
cur = ~cur
for nex, c in G[cur]:
if P[nex] != cur:
continue
maxbelow[cur] = max(maxbelow[cur], maxbelow[nex] + c, D[nex] + c)
maxabove = [0]*N
stack = [0]
while stack:
cur = stack.pop()
n = 0
children = []
vals = []
for nex, c in G[cur]:
if P[nex] == cur:
n += 1
stack.append(nex)
children.append((nex, c))
vals.append(max(maxbelow[nex] + c, D[nex] + c))
maxabove[nex] = max(maxabove[cur] + c, D[cur] + c)
if n > 0:
left = [0]*n
right = [0]*n
left[0] = vals[0]
for i in range(1, n):
left[i] = max(left[i-1], vals[i])
right[n-1] = vals[n-1]
for i in range(n-1)[::-1]:
right[i] = max(right[i+1], vals[i])
for i, nc in enumerate(children):
nex, c = nc
if i > 0:
maxabove[nex] = max(maxabove[nex], left[i-1] + c)
if i < n-1:
maxabove[nex] = max(maxabove[nex], right[i+1] + c)
for i in range(N):
print(max(maxbelow[i], maxabove[i]))ABC222 E - Red and Blue Tree
o 実装大変で、コーナーケースもやっかい。全部同じ頂点で、全く移動せず、どの辺も通らないテストケースひどくない?その場合は通る辺がないので、通った辺の色の数の差は0にしかならないw まあ、最短経路といっても、木なので1本しかないし、N=1000なら計算量も少ない、など気づけるのは基本。light blue #実装力 #コーナーケース 2023-11-29
ABC212 F - Greedy Takahashi
o すでに大晦日に入ってるが、2023年最後の精進がんばってるなう。自力ACいけた。ややこしすぎてコンテスト中に間に合う気がしないが、ダブリングという方針も見えたので、良かった。これ赤Diffで初めて自力ACしたのに似てるかも。次乗るバスは確定するので、次乗るバスを親とするバスのグラフを作る。ダブリングで最後に乗るバスを見つける。最初に乗る前の場合もあるので、if文注意。そういうのミスってデバッグでハマりそうである。ダブリングのコードはややこしいけど、無の境地でなんとかしろ。yellow #ダブリング 2023-12-31
import bisect, math
N, M, Q = map(int, input().split())
city = [[] for _ in range(N)]
buss = []
for _ in range(M):
a, b, s, t = map(int, input().split())
a, b = a-1, b-1
buss.append((a, b, s, t))
buss.sort(key=lambda x: x[2])
C = [[] for _ in range(M)]
for i, bus in enumerate(buss):
a, b, s, t = bus
city[a].append((s, i)) # 時刻とバス、時刻順
for i, bus in enumerate(buss):
a, b, s, t = bus
j = bisect.bisect_left(city[b], t, key=lambda x: x[0]) # 次乗るバス
if j < len(city[b]):
C[city[b][j][1]].append(i)
depth = [-1]*M
max_double = math.floor(math.log2(M))
parents = [[-1]*(M) for _ in range(max_double+1)]
for i in range(M)[::-1]:
if depth[i] >= 0:
continue
stack = [i]
while stack:
cur = stack.pop()
for nex in C[cur]:
depth[nex] = depth[cur] + 1
parents[0][nex] = cur
x = 0
while x < max_double:
if parents[x][parents[x][nex]] == -1:
break
parents[x+1][nex] = parents[x][parents[x][nex]]
x += 1
stack.append(nex)
ans = []
for _ in range(Q):
s, a, t = map(int, input().split())
a -= 1
# 最初に乗るバス
j = bisect.bisect_left(city[a], s, key=lambda x: x[0])
if j < len(city[a]):
cur = city[a][j][1]
x = max_double
while x >= 0:
# tの時点ですでに乗った最後のバスを探す
if parents[x][cur] != -1 and buss[parents[x][cur]][2] < t:
cur = parents[x][cur]
x -= 1
if t <= buss[cur][2]:
# これいるのか?上の遷移を見ると<tになってそうだが
# 最初のバスの場合は乗ってないかもしれないので必要
ans.append((buss[cur][0]+1,))
elif t <= buss[cur][3]:
ans.append((buss[cur][0]+1, buss[cur][1]+1))
else:
ans.append((buss[cur][1]+1,))
else:
ans.append((a+1,)) # バスに乗れない
for a in ans:
print(*a)ABC212 E - Safety Journey
o 通れない辺の数が最大5000ということで、遷移のコストを5000で済むようにすれば良い。light blue #DP 2023-12-30
ABC169 B - Multiplication 2
o サンプルからミスらず一発ACいけた。しかし、コードを書き始めて初めて罠に気づいたが。コードを書くことを通じて考えてるんだな。 2023-09-22
ABCの問題を思い出すシリーズ。茶色くらいの人へ。制限時間5分一発AC以外は挑戦失敗でお願いしまーす。
— chokudai(高橋 直大)@AtCoder社長 (@chokudai) September 20, 2023
B - Multiplication 2 https://t.co/r0lYxxwXJv
INF = 10**18
N = int(input())
A = list(map(int, input().split()))
A.sort(reverse=True)
if A[-1] == 0:
print(0)
else:
ans = 1
for a in A:
ans *= a
if ans > INF:
ans = -1
break
print(ans)ARC過去問
ARC153 D - Sum of Sum of Digits
難しかった記憶で再確認も、ムズすぎる。苦労して大部分思い出したけど、実際にこの問題に出会って、細かいところ詰められる気がしない。今さらながら次見たときのために、コードに日本語コメント追記した。上の以前書いたnoteにも同じところでハマったと書いてあるけど、読んでもわからん。気持ちはわかる。笑。しかしdpがdictで実装されてるけどn_carryって常に存在するのか?など忘れてて気になるところがどんどん出てくる。そもそもdictである必要もなくね?いや、bisectでn_carry求めてるから、このn_carryは必ずありうる値であることは確かだ。遷移ムッズイなぁ。dictじゃないほうが速かったりしないかな?確かに一番下の桁は10種類しかないし、下の5桁くらいになるとスカスカではあるけど、大して減らない気も。orange 2023-07-02
AGC過去問
AGC062 C - Mex of Subset Sum
x ★ 長期間解けずに放置してたのをようやくACした。ちょうど夏休み明けのこの機会に。提出してWAのまま放置してたのは現在この1問だけだったので気持ち悪かった。夏休みにFloor Sumとか最小費用流を履修して心のつかえが取れたので、これもついでにACしておく。ようやく解説を読んだ。これは難しい。TLEしない証明が解説に書かれているけどこんなことを自力で短時間で考える力は、今のぼくには間違いなくない。解説を見ながら書いたコードで、04_handmade_11という最後のテストケースがTLEする。テストケースが公開されているので、確認すると、原因は明らかだった。入力次第ですごい大規模なセットを生成するコードになっていて、それを潰すテストケースだった。対処としては、打ち切るだけで良い。if s < a:の中の、if len(ex) >= K:のところ。これがfor文の外に出ていて、全部追加してからチェックするコードになっていた。Aの制約条件が10^15。そりゃ無理だわ。でも解説ACだから気づかないのであって、自力でロジックを組み立てればこのようなミスはしないかもしれない。ただ、自力で考え抜くにはかなり難易度が高い問題であることは、間違いない。今は中途半端に手をつけてACできてない問題がなくなったということでスッキリしておこう。激ムズだけど、一応理解はしたのだから、今後の糧になるはずだ。yellow 2023-08-17
N, K = map(int, input().split())
A = list(map(int, input().split()))
A.sort()
s = 0
ex = set()
fixed = False
for a in A:
if s < a:
for x in range(s+1, a):
ex.add(x)
if len(ex) >= K:
s += a
fixed = True
break
if fixed:
break
for x in sorted(ex):
if x > s:
break
ex.add(x+a)
else: # a <= s
nex = set()
exlist = sorted(ex)
lenex = len(ex)
i = 0
for x in exlist:
if x >= a:
break
nex.add(x)
if len(nex) >= K:
ex = nex
s += a
break
j = 0
for x in exlist[::-1]:
if x < a:
break
if x-a in ex:
nex.add(x)
limit = s + 1 - a
for x in exlist[::-1]:
if x < limit:
break
nex.add(x+a)
ex = nex
s += a
exlist = sorted(ex)
print(*exlist[:K], *range(s+1, s+1+K-len(exlist))).
