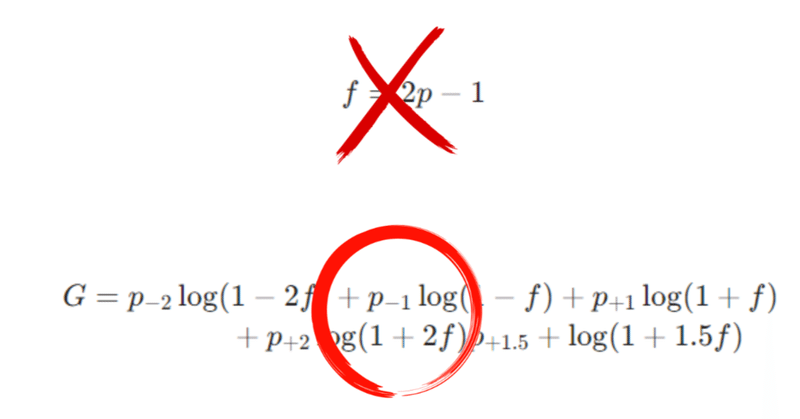
ブラックジャックにおける正しいケリー基準
ケリー基準とは、勝敗のある賭けにおいて、複利効果を最大にするような賭け額を提示してくれる式です。特に、勝ったら1倍勝つ、負けたら失うような場合には以下のようになります。
$$
betsize= ev \times asset
$$
evとは期待値のことで、assetとは総資産のことです。例えば期待値が+0.01で総資産が100万円あったとしたら、一回に1万円ベッドするのが最も複利効果を最大にするという事です。インターネットで調べると大体この式が出てくると思います。
ブラックジャックに対しても、期待値が+1%の場合、勝利する確率を50.5%、敗北する可能性を49.5%とし、勝ったら1倍勝ち、負けたら失うというように単純化すれば、上記の式を適用できます。
しかしこれは、ダブルやスプリットによる2倍勝ちや2倍負け、ブラックジャックにによる1.5倍勝ち、プッシュによる±0等全てを無視しているので、その精度には疑問が残ります。
結論から言うと、ブラックジャックにおいては、上記の式と実際に最適なベッドサイズの間にはかなりの乖離があります。その証明をするのですが、数学的な話が続くので、嫌な人は適当に飛ばしてください。
ケリー基準の導出
インターネットで調べても、なぜケリー基準がこの式になるのかというのはなかなか出てこなかったので、ここから始めます。まず、確率pで勝利し、勝利した場合資産が$${1+f}$$倍になり、敗北した場合資産が$${1-f}$$倍になる試行を$${n}$$回繰り返した時の結果は、以下の式で表せます。
$$
y=(1+f)^{pn}(1-f)^{(1-p)n}
$$
総資産に対して常に一定の割合$${f}$$を賭けるので、実際の賭け額に関わらずその結果は、資産が$${(1+f)}$$倍になるか$${(1-f)}$$倍になるかしかありません。これを$${n}$$回繰り返すと、理想的には$${pn}$$回勝利し、$${(1-p)n}$$回敗北するので、上記の式になります。
無限回の試行を繰り返した時の複利が最大になるような$${f}$$を求めます。無限回繰り返す理由は、無限回繰り返さないと$${pn}$$と$${(1-p)n}$$の値が理想的にならないからです。有限回の試行では$${pn}$$と$${(1-p)n}$$の値にはばらつきがあるので計算が複雑になってしまいます。
$$
G=\lim_{n \rightarrow \infty}\frac{1}{n}\log((1+f)^{pn}(1-f)^{(1-p)n})
$$
これを変形すると、以下のようになります。
$$
G=p\log(1+f)+(1-p)\log(1-f)
$$
これの最大値を求めたいので$${f}$$について微分して極を探します。
$$
G'=\frac{p}{1+f}-\frac{1-p}{1-f}
=\frac{2p-1-f}{(1+f)(1-f)}
$$
増減表を書いたりなんだりすると(書かなくても見たら分かると思うが)、
$$
f=2p-1
$$
で最大値を取る。
ここで$${2p-1}$$は、期待値に等しいので、総資産に対して最適なベッドサイズの割合$${f}$$は期待値と等しいことが分かる。それで、この値は有限回の試行でも正しいらしい。
ブラックジャックへの適用
これをブラックジャックに適用するとこうなる。
$$
G=p_{(-2)}\log(1-2f)+p_{(-1)}\log(1-f)+p_{(+1)}\log(1+f)\\ +p_{(+2)}\log(1+2f)+p_{(+1.5)}\log(1+1.5f)
$$
$${p_{(n)}}$$は$${n}$$倍勝ち(負け)になる確率です。これの$${G}$$が最大となるような$${f}$$を求めればよい。
が、この式は多分代数的に解くことが出来ないので、$${p}$$に実際の値を入れてコンピューターに解いてもらう。
対象にするデッキの構成はこれ。ルールはEvolutionのインフィニットブラックジャックで計算する。
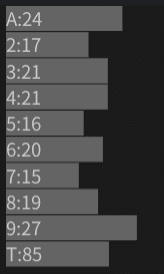
期待値:+0.01533

これをwolfram alphaに突っ込むとこうなる

単純化されたケリー基準から導き出された値(0.0153)よりもかなり低い値(0.0131)が導き出された。普通のケリー基準においても、期待値がいくら高かろうと勝利確率が低いとベッドサイズは小さくなっていくので、ダブルやブラックジャックといった確率の低い結果を考慮するとベッドサイズが小さくなるのは当然といえば当然だろう。
実際この差はどれくらいなのか
上記のデッキに対して300回賭けを行うシミュレーションを10000回行った結果を比較してみます。
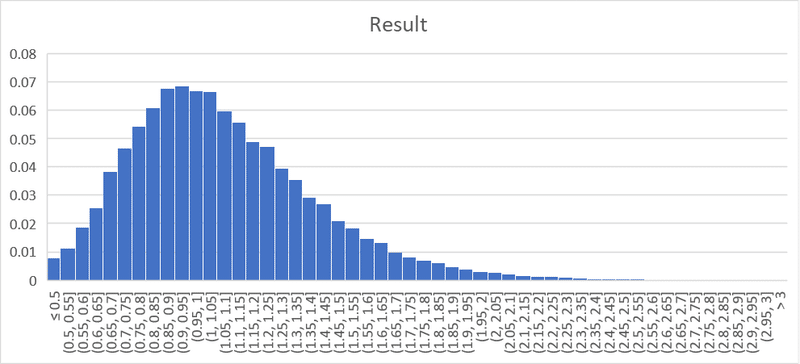
単純化されたケリー基準

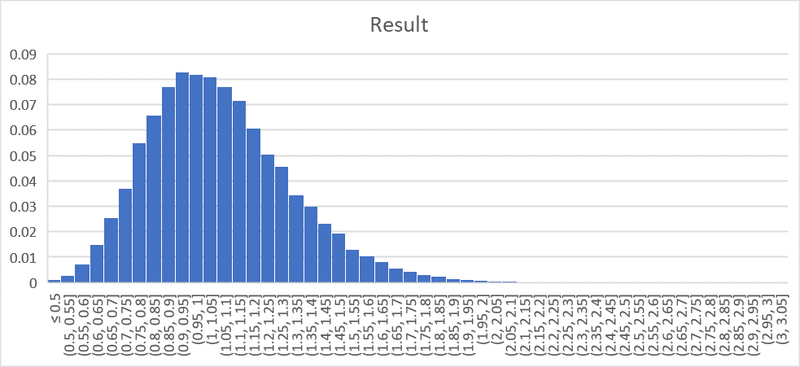
正確なケリー基準

結論
単純化されたケリー基準の方が平均値は高いが、中央値が低くなっていることが分かる。単純化されたケリー基準の方が掛け金が大きいから、平均値が高くなったり結果によりばらつきが出るのは当然だが、中央値が低くなるのはかなり興味深いだろう。中央値が低いということは、それだけ儲かる可能性が低くなる、逆に言えば損する可能性が高くなるということだ。
単純化されたケリー基準を使うと、儲かる可能性は低くなるが、儲かったときのリターンは大きくなる。一方で、損する可能性は高くなり、損する額も高くなるということだ。つまり、よりギャンブル性のある結果をもたらすということになる。
長期的にブラックジャックをする場合、正確なケリー基準に基づいて賭けた方が、結果は安定するし、儲かる可能性が高いということが示された。
実際のブラックジャックへの適用
正確なケリー基準を使うためには、各結果が起こる確率を求めないといけないので、使えないように思えるかもしれません。が、私が開発したこちらのツールを使えば、正確なケリー基準を計算することが出来る…ようにしたいので近いうちにアップデートします。アップデートしました。
ランドカジノでは、単純化されたケリー基準に対して0.85倍くらいの値を掛けて運用しておけば問題無いと思われます。
余談
「ブラックジャック ケリー基準」で調べてgoogle検索で一番上位に出てくるブログには相当めちゃくちゃな内容が書いてある。ケリー基準を超解釈し、必ずブラックジャックが起きる前提でベッドサイズを計算し、期待値がマイナスであるのにも関わらず一回15%!を賭けるのが数学的に理想だというとんでもない結論に至っている。皆様にはこのようなでたらめだけどSEOだけ頑張ってる記事に惑わされないでもらいたい。中学レベルの数学が分かっていればおかしいなと思えるはずなので、惑わされてしまった人は数学を勉強しなおすことをお勧めする。ギャンブルや投資は深く数学と結びついているので、数学の理解は結果的にそれらで良い結果を出すことにも繋がるはずです。
この記事が気に入ったらサポートをしてみませんか?
