こんにちは、青の統計学です。

WEBサイト「青の統計学」やX「青の統計学」から来ていただいた方、ありがとうございます。
noteでは、チートシート完全版を投稿しています。

統計検定2級は、大学基礎科目レベルの統計学の知識の習得とその活用について理解しているか問われる検定で、機械学習やデータ分析を行う際に必要な基礎知識が身につきます。

データサイエンティストという仕事や、機械学習周りの知識に興味がある方はこちらの記事もおすすめです。

統計検定2級チートシート

このチートシートの特徴

この教材は、以下の方におすすめです！

• 試験日まで近いが、なかなか重要事項の理解が進まない方

• 一通り教科書や問題集は読んでみたつもりだけど、抜け漏れがないか心配な方

• 分散分析の分野など、難しい事項の理解が進まない方

• 覚える部分は覚えたけど、裏側のアルゴリズムや関係する手法、発展的な内容などに興味がある方

• 正直、教科書だと数式だらけでわかりづらい方

• 試験に落ちてしまった方

当時筆者も統計検定2級に向けて、覚えることは覚えましたが、数値や条件が少し違うと間違えてしまうという応用が効かないことが悩みでした。

など、角度を変えた質問が飛んでくると、よくわからないという状態でした。
皆さんは、ちゃんと答えられますか？

「合格後のキャリアやスキルアップを目的とするなら本質的な理解をして欲しい」

「こんな教材があると試験前の自分は助かる」

「試験直前の朝に見たかった」

以上のような思想で時間をかけて作成しました。
合計３万字をこえる大作になっております。

また筆者は、これまで別サイト「青の統計学-Data Science School-」で統計関連の記事を約110記事を書いておりますが、このチートシートと各コンテンツを有機的に繋げて、学習効率が最大化されるように書いています。

使い方①

各項目についての応用的な補足や証明については、別サイト「青の統計学-Data Science School-」の参考コンテンツを豊富に貼り付けておりますので、並行して学習に役立てていただければと思います。

使い方②

項目の最初に押さえるべき「チートシートポイント」を箇条書きで記載しています。本質的な理解のために説明や補足、背景となる知識を下部に詳細に記載しています。試験までお時間がある場合は、説明まで目を通していただけると幸いです。

使い方③

難易度の低い順にセクションを並べており、以下のような基準で選定しています。
難易度⭐️→統計検定3級レベル。わかっていないと困る。
難易度⭐️⭐️→最低限理解していないと合格は難しい。
難易度⭐️⭐️⭐️→合格を確かなものにするために必要。
難易度⭐️⭐️⭐️⭐️→細かい失点がなければ満点を狙える実力。
補足：該当セクションで補足しておく事項を説明しています。要チェックです。
発展：2級だと問題で触れられない可能性は高いですが、深い理解や今後のために説明している部分です。

使い方④

所々に図解をしていますが、図を作るために使ったpythonコードを最後に載せております。数値を色々変えてみて理解を深めていただければと思います。

さてお待たせしました！
ここからチートシートになります。
かなり分量が多いですが、試験当日の役に立つと思います！！

ご武運を

期待値と分散｜難易度⭐️

• 期待値（離散）：$${E[X]=\sum_i x_ip(x_i)}$$

• 期待値（連続）：$${E[X]=\int_i xf(x)dx}$$

• 期待値は各実現値を確率と掛けて和をとったもので$${E(aX+b)=aE(X)+b}$$のような線形性がある。

• 分散：$${V(X)=E[(X-E[X])^2]=E(X^2)-[E(X)]^2}$$

• 分散は、確率変数に影響のない定数項が追加されても数値に影響がない

期待値

期待値は、確率変数が取りうる値の加重平均です。
この「加重」は、各値が発生する確率によって行われます。
形式的には、確率変数 $${X}$$の期待値$${E(X)}$$ は$${X}$$ が取りうる各値とその値が発生する確率の積の総和として計算されます。

離散確率変数の場合

$${E[X]=\sum_i x_ip(x_i)}$$

＊本記事でも区別して書いていますが、大文字の$${X}$$と小文字の$${x}$$は全くの別物です。
前者は確率変数であり、後者はその確率変数が取りうる一つの実現値です。

連続確率変数の場合

$${E[X]=\int xf(x)dx}$$

$${f(x)}$$は確率密度関数ですね。
総和が１になります。

分散（variance）

分散は、確率変数がその期待値からどれだけ散らばっているかを示す尺度です。
確率変数の平均からの偏差の二乗の期待値として計算され、この定義により、値の散らばり具合を正確に把握することができます。

$${V(X)=E[(X-E[X])^2]}$$

この式はまた、次のように簡化して表現することもできます（二次の展開を使用）

$${V(X)=E(X^2)-[E(X)]^2}$$

統計検定2級で覚えておきたい期待値と分散の性質は以下の二点です。

期待値の線形性: 期待値は線形演算子です。
つまり、任意の定数 $${a}$$ と $${b}$$ に対して以下が成り立ちます。

$${E(aX+b)=aE(X)+b}$$

分散のスケーリング：分散は期待値との関係から以下のような性質を持ちます。

$${Var(aX+b)=a^2Var(X)}$$

確率変数に影響のない定数項が追加されても分散には影響がないということですね。

発展｜モーメント

モーメントは確率分布の形状に関する情報を提供する数学的な特性です。
定義としては、確率変数のべき乗の期待値です。
特に、確率変数 $${X}$$の$${k}$$次の原点モーメント $${E(X^k)}$$は、$${X}$$の $${k}$$ 乗の期待値です。

一次モーメント（期待値）は分布の平均位置を示し、二次モーメント（分散）は分布の広がりを示します。
さらに、三次のモーメントは分布の歪度（非対称性）を、四次のモーメントは尖度（ピークの鋭さと尾部の厚み）を表します。

モーメントや確率母関数は、統計検定準一級の範囲ですので、詳しく勉強したい方は以下の記事をご覧ください。

補足｜尖度と歪度

統計検定2級では、上述した3次と4次のモーメントを使った尖度と歪度の理解をとう問題もあります。

主にデータの視覚的分析の文脈で使われるので、図と一緒に出題されます。
実は計算方法はいくつかあるのですが、ここではモーメントを使った方法をご紹介します。

歪度（skewness）

歪度は、分布の非対称性を測定する指標です。
分布が左右対称である場合、歪度はゼロになります。
正の歪度は、分布の右尾（右裾）が左尾よりも長いことを示し、負の歪度は左尾が右尾よりも長いことを示します。

$${skewness=\frac{E(X-\mu)^3}{\sigma^3}}$$

データの平均からの偏差を三乗して平均化し、標準偏差の3乗で割ることで標準化しています。
これにより、データセットが正の歪度（右に長い尾）を持つか、負の歪度（左に長い尾）を持つかが判断されます。

尖度（kurtosis）

尖度は、分布の尾部の重さ（ピークの尖り具合と尾部の厚み）を測定します。
尖度が高い分布は、中心付近がより尖り（ピークが高い）と同時に尾部が厚いことを示し、低い尖度はより平坦な分布を意味します。

$${kurtosis=\frac{E(X-\mu)^4}{\sigma^4}}$$

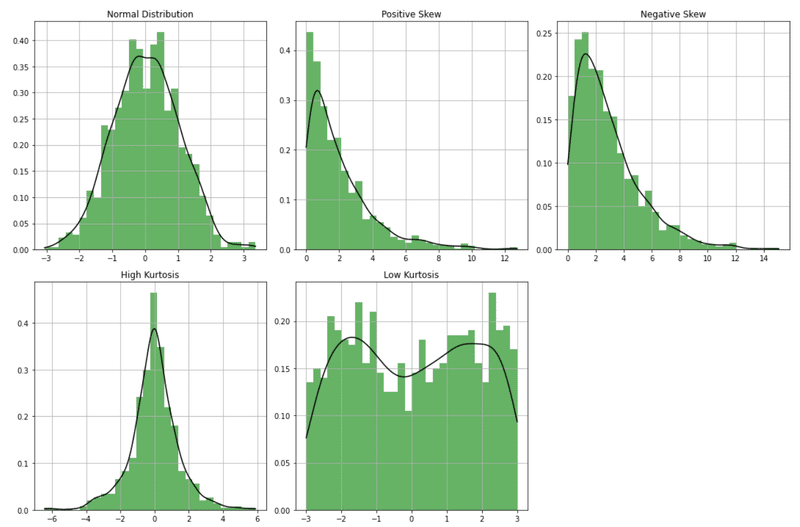
参考までに以下が歪度と尖度が高い低い、の例です。
やや字が小さいですが、左上が正規分布です。