ご覧いただきありがとうございます。
こちらのnoteは、量子力学に出てくる重要な用語や方程式、概念をまとめたブログ記事の下書きを全文公開しています。

• 量子力学の入り口に立ちたい人

• 何から勉強すればいいか分からない人

• 量子力学を学び始めていて、用語の確認をしたい人

への道標として書きました。ぜひご活用いただければと思います。
もちろん、量子力学に何となく興味がある人もぜひご覧になっていってください。

正式に公開した記事はこちらにあります。
興味のある方は、是非クリックしてご覧いただければ嬉しいです！

波動性と粒子性 Wave/particle nature

光や電子は「波動」と「粒子」の二つの性質を合わせ持ちます。この性質を発見した実験の一つが二重スリット実験です。

現象に応じて、波動性と粒子性のうちどちらか一方の性質だけが顕在化することがあります。
人間は光や電子の実態を観測できませんが、量子現象は二つの性質が根底にあります。

波動関数 Wave function

ニュートン力学には登場しない量子力学特有の概念で、「状態」を記述したものです。

$${F=ma}$$などの古典物理学の運動方程式では、状態自体を表した物理量(長さ、質量、時間など)や関数はありません。
しかし量子力学の中では抽象的な状態そのものを関数として導入しています。

$${\phi, \psi}$$で書かれることが多いです。

シュレディンガー方程式 Schrödinger equation

シュレディンガーさんが天下り的に考案した状態方程式で(1)式や(2)式のように表されます。

$$
i\hbar\frac{\partial \phi(\boldsymbol r,t)}{\partial t}=\mathcal{H}\phi(\boldsymbol r.t)\\[4mm]
\mathcal{H}\phi(\boldsymbol r) =E\phi(\boldsymbol r)
$$

最初の式を「時間依存シュレディンガー方程式」、二番目の式を「時間に依存しないシュレディンガー方程式」といいます。
$${E}$$はエネルギーの次元を持ち「固有エネルギーeigen energy」とよばれます。

$${\mathcal{H}}$$はハミルトニアン Hamiltonianといって、運動エネルギーとポテンシャルエネルギーの和で表されます。

$$
\\[3mm]
\mathcal{H}=\frac{\boldsymbol p^{2}} {2m}+V(\boldsymbol r)=-\frac{\hbar^{2}}{2m}\Delta+V(\boldsymbol r)
$$

運動量$${\boldsymbol p}$$の項がラプラシアンで書かれた形に変わっていますが、こちらはニュートン力学では考えられない、量子力学特有の式変形です。

シュレディンガー方程式は形式的に、拡散方程式と呼ばれる微分方程式の形をしており、量子力学的現象をうまく記述することができます。

いくつかの方法でこれらの式の妥当性を証明することができますが、そもそもなぜこの式が成り立つのかについてはよくわかっていません。

確率解釈 Stochastic interpretation

シュレディンガー方程式自体は単なる拡散方程式の形をしていますから、そこで解かれた波動関数とは何なのか、量子力学の成立に伴っていくつかの解釈が提唱されました。

現在、最も支持されている解釈の一つが確率解釈です。この説によると波動関数の二乗絶対値がその位置に粒子が存在する確率を表します。

粒子がある位置$${\boldsymbol x}$$に存在する確率密度 probability density $${\rho}$$は次のように書きます。

$$
\rho=\braket{\phi_r|\phi_r}=|\phi_r|^{2}
$$

波動関数が空間的に局在しているなら、微視的には粒子が確率的に存在していても、より大きいスケールの視点ではまるで一つの粒のように見えます。そういった意味で確率解釈は粒子性と波動性の両方をうまく取り込んだ解釈と言えるでしょう。

量子力学の波動関数が一体なんであるのかは、専門家の間でも細かい解釈の違いがあります。

行列形式のシュレディンガー方程式

シュレディンガー方程式は式変形によって解析的 Analyticalに解くほかに、代数的 Algebraicな行列計算によっても解くことができます。

この時、シュレディンガー方程式は次のような、関数のシュレディンガー方程式と似たような形をした行列の式になります。

$$
\begin{pmatrix}
\mathcal{H_{11}} & \mathcal{H_{12}} \\
\mathcal{H_{21}} & \mathcal{H_{22}} \\
\end{pmatrix}
\begin{pmatrix}
\phi_1 \\
\phi_2\\
\end{pmatrix}
=
\begin{pmatrix}
E&0\\
0&E\\
\end{pmatrix}
\begin{pmatrix}
\phi_1 \\
\phi_2\\
\end{pmatrix}
$$

関数との違いはハミルトニアンが行列になり、波動関数が列ベクトルになっていることです。

行列は英語でmatrix(数学的には変換の意)ですから、行列は通常、列ベクトルに作用させることで、別の行列を生成するために用いられます。

一方、シュレディンガー方程式ではハミルトニアンの行列を波動関数に作用させても、右辺で波動関数は変化していません。代わりに固有エネルギーがはき出された形になっています。つまり固有値方程式 Characteristic equationの形をしています。

エネルギーを求めるためには下に書いた行列式を計算して固有値と固有ベクトルを求めます。

$$
\begin{vmatrix}
\mathcal{H_{11}}-E & \mathcal{H_{12}} \\
\mathcal{H_{21}} & \mathcal{H_{22}} -E \\
\end{vmatrix}
=0
$$

この行列式を永年方程式 Secular equationと呼ぶことがあります。

シュレディンガー方程式ではこの時の固有値を「固有エネルギー Eigen energy」、固有ベクトルを「固有状態 Eigenstate 」と呼びます。

このように量子力学の大きな特徴として、解析と代数の両方で互いに等価な解法が存在します。

特に代数的な解法は数値計算と非常に相性が良いことで知られています。

エルミート行列 Hermitean matrix

ハミルトン行列はエルミート行列 Hermitian matrix と呼ばれる行列でなければなりません。

エルミート行列とは「複素転置行列が元の行列と等しくなるような行列」です。

$$
H=H^\dagger=\begin{pmatrix}
\mathcal{H_{11}} & \mathcal{H_{a}+iH_b} \\
\mathcal{H_{a}-iH_b} & \mathcal{H_{22}} \\
\end{pmatrix}
$$

$${H^\dagger}$$の肩に乗っている記号はダガー Daggerといい「複素共役をかけて転置する」という意味です。

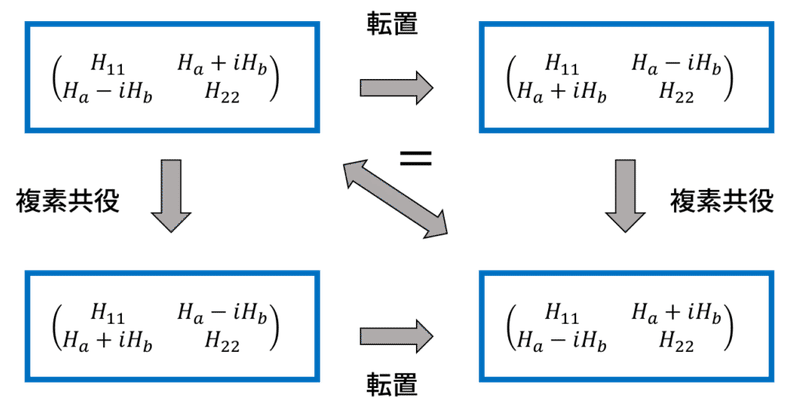
このような制約の背景には、シュレディンガー方程式の固有エネルギーが実数になるという要請と関係があります。

演算子 Operator

量子力学ではハミルトニアンを演算子とみなす見方があります。ふつう、演算子と言えば四則演算子が思い浮かぶかと思いますが、量子力学で扱う演算子はどちらかというと微分演算子やナブラ演算子に近いです。

演算子を作用させることは波動関数に対する何らかの操作を表しています。例えば下の式を例にしましょう。

$$
\frac{d}{dx}e^{ax}=ae^{ax}
$$

$${e^{ax}}$$を微分した結果、元の$${e^{ax}}$$の係数に$${a}$$が掛かっています。見方を変えると、関数に演算子を作用させることで、$${a}$$という値がはき出されたように見えます。

今度はシュレディンガー方程式に対しても同じような見方をします。ハミルトニアンを演算子$${\hat{\mathcal{H}}}$$(エイチハット)とみなすと、シュレディンガー方程式は「波動関数にハミルトン演算子を作用させた結果、エネルギーがはき出された」ように見えます。このとき、演算の前後で波動関数は変化しません。

このような操作は、特定の別の演算子でも行うことができ、ハミルトン演算子のほかにも、さまざまな種類が存在します。

例えばある状態の運動量や位置を求めたいときは、数式上では波動関数に運動量演算子や位置演算子を作用させることで表します。

このように、シュレディンガー方程式は演算子や行列によって状態(波動関数)を変化させたり、物理量などの情報を取り出すことができます。

ハミルトニアンはエルミート行列であることが必須でしたが、ハミルトン演算子も同様にエルミート演算子と呼ばれる性質を持つ演算子でなくてはなりません。

オブザーバブル Observable

演算子の中でも「観測量(長さ、時間、エネルギーなど)を取り出せる演算子」が持つ性質をオブザーバブル Observableといいます。

私たちは波動関数を直接観測することはできず、実験によって物理量を「観測・測定」して状態を求めます。実験による物理量の測定は、数式では状態にオブザーバブルな演算子を作用させることで表現します。

物理量は観測可能な実数なので、オブザーバブルな演算子には「作用させると実数が取り出せる」という制約が掛かってきます。実はこの制約が「演算子がエルミート演算子」であることなのです。

交換関係 Commutation relations

行列計算では二つの行列のどちらを先にかけるかで、結果が変わることがありましたね。
同様に演算子も二つの演算子を入れ替えると結果が変わることがあります。

演算子の入れ替えに関して値がどのように変化するかを示した関係を交換関係と言います。

交換関係は二つの演算子$${\hat{A}, \hat{B}}$$に対して次の計算をして確かめます。

$$
[\hat{A},\hat{B}]=\hat{A}\hat{B}-\hat{B}\hat{A}
$$

上式は交換子 Commutator、あるいはポアソン括弧式 Poisson bracketなどといい、互いに演算子を入れ替えて差をとる操作を行います。

もし交換関係が0なら「交換関係が成り立つ」あるいは「可換である」といい、演算子は自由に入れ替え可能です。しかし0でなければ演算子の入れ替えで得られる結果が変わります。

交換関係が成り立つ場合、二つの演算子に対して状態は一つに決まり「同時固有状態 Simultaneous eigenstatesをもつ」といいます。

それぞれの演算子がオブザーバブルかつ可換なら、二つの物理量は同時に観測することができます。

逆に可換でなければ、演算子のどちらかを先に作用させるかで状態が変わってしまうので、実験でも同じ状態に対して二つの物理量を同時に計測することはできません。

交換関係は不確定性原理の説明にも用いられます。

ハイゼンベルグの不確定性原理 Heisenberg uncertainty principle

位置と運動量を高精度に同時には求められないという原理です。

運動量を速度とした書籍やサイトもありますが、確率解釈で説明したように粒子は確率的に存在します。そのため確率的に存在する粒子に対して速度は定義されないため、運動量で書くのが正確です。

逆に速度が定義されない確率的な粒子にも、運動量に相当する何かが存在するともいえます。

不確定性原理を交換子で表現すると次の通りです。

$$
[\hat{\boldsymbol x},\hat{\boldsymbol p}]=i\hbar
$$

この式は可換ではなく、同時固有状態を持ちません。したがって位置と運動量を同時に計測することができず、不確定性原理を満足します。

以上で、今回の記事は以上です。
ご覧いただきありがとうございました。

他の量子力学の記事を始め、皆さんの学習に役立つ情報を下のサイトに公開しています。リンクをクリックして、ぜひご覧ください。