重回帰式（多変量解析）で独立変数から従属変数を推定する式が既にある場合でも、新たにデータが取得できて、それを考慮した重回帰式を作りたい時があります。元のデータに新しいデータを追加して、再度回帰分析をができるなら、それでよいのですが、新しいデータが逐次生じて、常に回帰式を更新し続けたい場合は、一から回帰分析をするのは手間ですし、元データが膨大であったり、わからなくなっているなどと場合は不可能です。
　そこで重回帰式の係数を新しいデータで補正する方法を検討しました。

回帰式

$$
y=a_0+a_1x_1+a_2x_2+…+a_ix_i     (1)
$$

に対して、$${y}$$の係数$${a_i}$$に対する全微分の式は

$$
dy=\frac{\partial y}{\partial a_0}da_0+\frac{\partial y}{\partial a_1}da_1+\frac{\partial y}{\partial a_2}da_2+…+\frac{\partial y}{\partial a_n}da_n     (2)
$$

何らかの補正をした後の新しい回帰式は以下であらわされるとすると

$$
y'=a'_0+a'_1x_1+a'_2x_2+…+a'_nx_n     (3)
$$

(3) - (1) は

$$
y'-y=(a'_0-a_0)+(a'_1-a_1)x_1+(a'_2-a_2)x_2+…+(a'_n-a_n)x_n     (4)
$$

ここで　(2) = (4)と考え、$${\partial a_i = da_i}$$　とみなす、$${\partial y = \frac{dy}{n+1}}$$　のように各項に$${dy}$$が均等に配分されると仮定すると、

$$
a'_i = \frac{dy}{(n+1)x_i} + a_i     (5)
$$

ここで　$${i=0…n}$$、$${x_0 = 1}$$、また、$${dy = y'-y}$$。

　新しいデータを全面的に取り入れると影響が大きくなるので、$${係数k( k=0…1)}$$を用いて、

$$
a'_i = k\frac{y'-y}{(n+1)x_i} + a_i     (6)
$$

とするのが無難と思います。

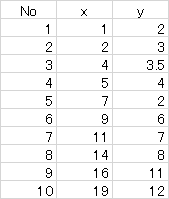
簡単な例
今、表のようなデータがあった時、これの回帰式を求めると
$${y=a_0+a_1 x=0.9151+0.5608x}$$でした。

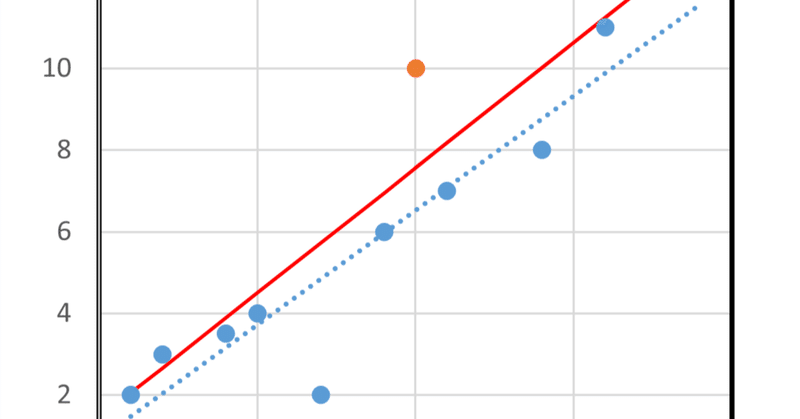
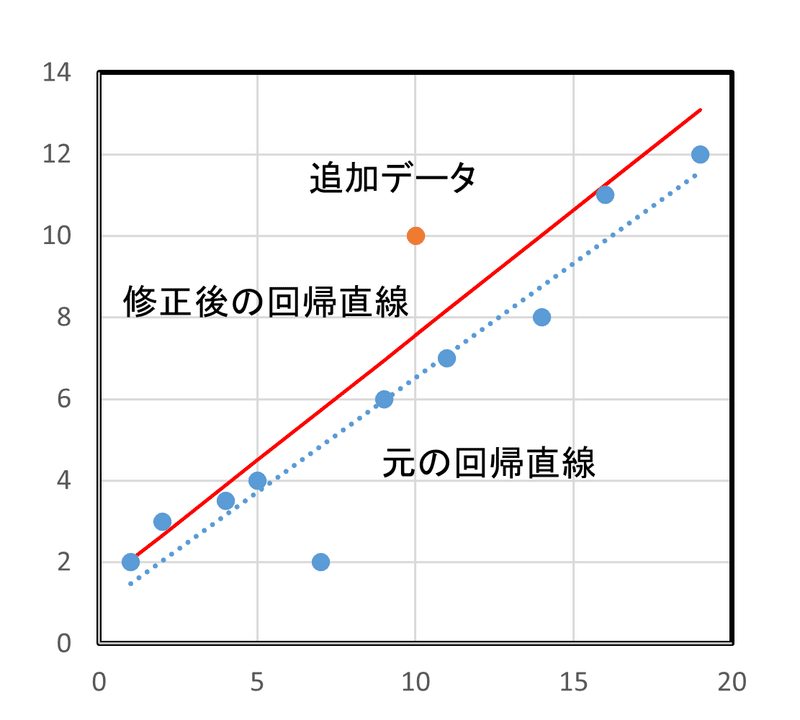
これに$${(x, y) =(10,10)}$$を上記の方法で追加すると、
$${y=a_0+a_1 x=1.4366+0.6129x ,  ( k=0.3)}$$となりました。
　結果を図に示します。水色の点が元のデータ、水色の破線が元のデータだけの回帰直線、オレンジの点が追加データ、赤線がオレンジで修正した回帰直線です。元の回帰直線の傾向を持ちながら、追加データ側にシフトしているのがわかります。

#重回帰分析 , #多変量解析 , #逐次修正