キューブラッシュにおける角度の概念を突き詰めると, 一を聞いて十を知るようにして, 最終的には直感的には思い付かないような気付きを与えてくれる.
それを支えるのが数学である.
この記事はかつて公開した「数学で避けるキューブラッシュ このように求めるのだ」という動画の内容を再構築したものである.
https://youtu.be/TfFWZoEgY34
https://youtu.be/n5qqvnECaUI

自機の狙い方の特徴

キューブが自機を狙って加速するときの角度には, ある特徴がある.
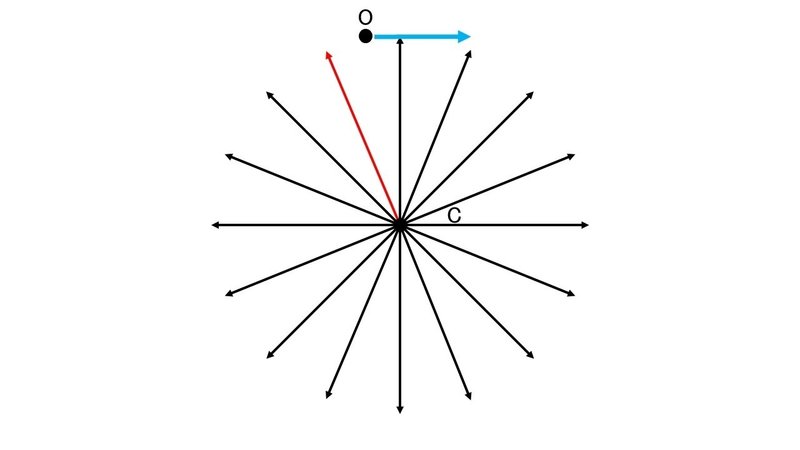
キューブはどの角度にでも好き勝手に加速できるわけではなく, 1周360°を32等分した11.25°刻みでしか加速できない.

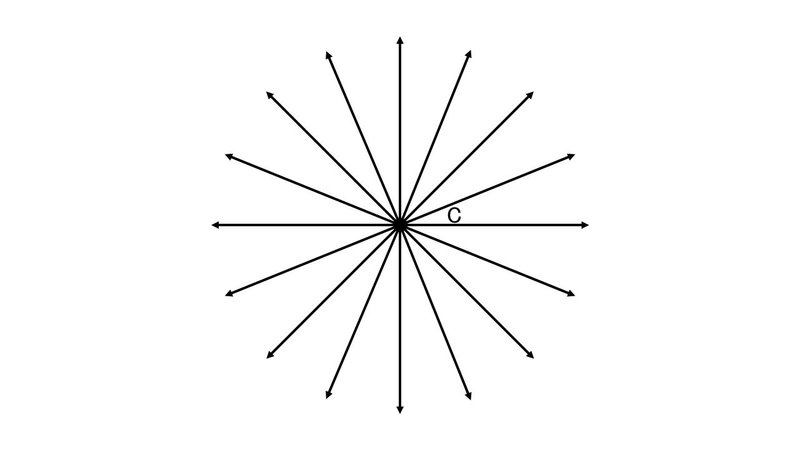
上の図はその様子を表したもので, 少し簡略化して, 32等分ではなく16等分として描いてある. 図中の点Cがキューブの位置を表す.
いずれにしても, キューブの軌道は「飛び飛び」の状態になっており, 「中間の状態が存在しない」という特徴がある.
そのような特徴のことを「離散(discrete)」という. 対になる概念は「連続(continuance)」である.

ちなみに, ゲーム中ジャンパーが吐いてくるばら撒き弾の軌道が, 1周を16等分したものとなっており, キューブはその倍の精度で自機を狙って来るということになる.

キューブは2択のどちらを選ぶのか

もしも自機が, 考えられ得る軌道のいずれかに重なっていた場合, キューブはその軌道を使って自機に突っ込んで来るのは自明のこととしてよいと思う.

では, 自機が軌道の候補に挟まれた中間の位置にいた場合に, キューブはどのように動くのであろうか.
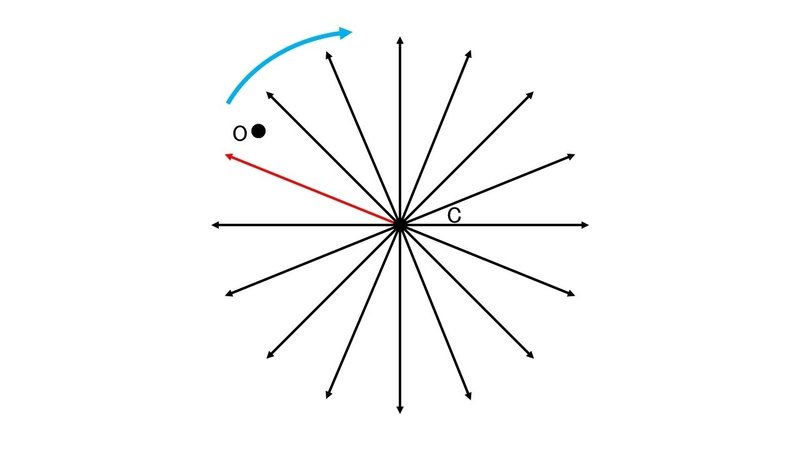
そのような状況を表したのが次の図である.

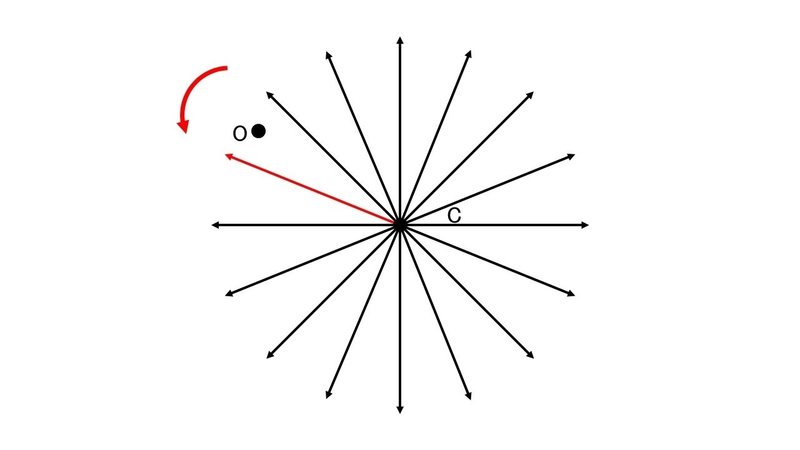
上の図で点Oは自機の位置を表している. 点Oは軌道の候補に挟まれている.
このような場合は, キューブを中心として自機よりも反時計回りの位置にある軌道が選択される.

ちなみに, この性質はキューブに限った話ではなく, 砲台の弾に関しても同じ性質があるようで, 同じx座標にある上下の砲台から同時に自機狙い弾を撃たれたときに, 非対称な撃たれ方をする.
一番分かりやすいと思われるのが6面の細道で, 自機を細道の中心線に置いたとしても, 天井の砲台は自機の鼻先をかすめるような斜めの弾を撃つのに対し, 床の砲台は自機の下を通る水平な弾を撃つというような現象が起こる.
このような性質を利用すれば, 弾の撃たせ方を工夫して弾を無視できる座標を見付けることができるようになるので, 画面から受け取る情報量を減らして道中を少し楽に進めるようになるという意味で, 覚えておいて決して損はない.

キューブを避ける動きの大原則

キューブの軌道の選択の性質から, 極めて単純な大原則がすぐに導かれる.
キューブを避ける際は, キューブを中心として時計回りに動いた方が, キューブを避けられる可能性が高いということである.

現実世界の乗り物でもそうだが, 軌道が交差するから衝突も起こるのだ.
そうであるならば, 衝突を防ぐためには軌道の交差を端から無くしてしまえばよいのである.
それをしているのが高速道路や新幹線で, 立体交差ばかりで構成されていて他の交通と交差するという状況が初めからない, すなわち急なブレーキを扱う必要がそもそもないように設計されており, それにより高速運転が可能になるのである.

反時計回りに動くということは, キューブの軌道と交差するということを意味する.
時計回りで動くと, 衝突以前に軌道との交差すらしないのである.

もっとも, これはあくまでも「原則」であり, 例外もあるといえばある.
特に全避けともなると, キューブの出現の形によっては, 掟破りの反時計回りもやむを得ない場面がある.
その場合は, 距離に余裕がなければならなかったり, 自機のスピードを上げて振り切る必要があったりする(最低でも3速はほしい).

上にあるキューブと下にあるキューブの違い

それでは, 大原則をどのように実際の避けに適用するのか, まずは簡単な例として, 自機よりも上にあるキューブと, 自機よりも下にあるキューブの違いを比較するところから.

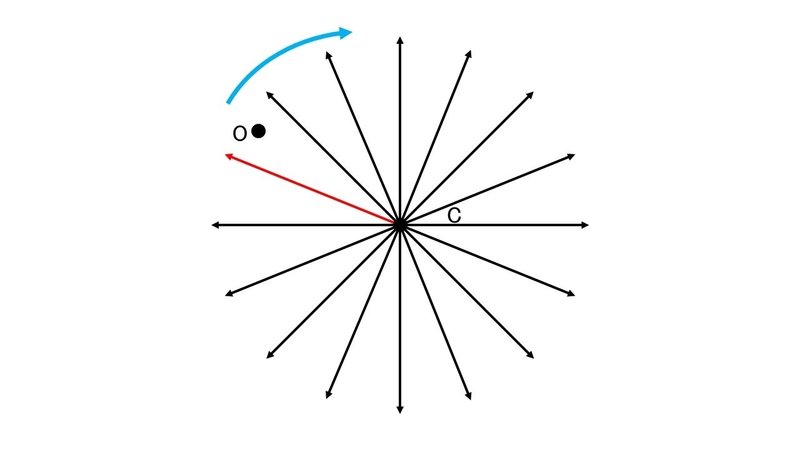
まず, 自機よりも上にあるキューブは, 自機の鼻先を狙って来る傾向にあることが次の図より分かる.
よって, そのようなキューブを左右の動きで避けるとしたら, 自機を左に動かすと, 避ける動きとしては安全なものになる.

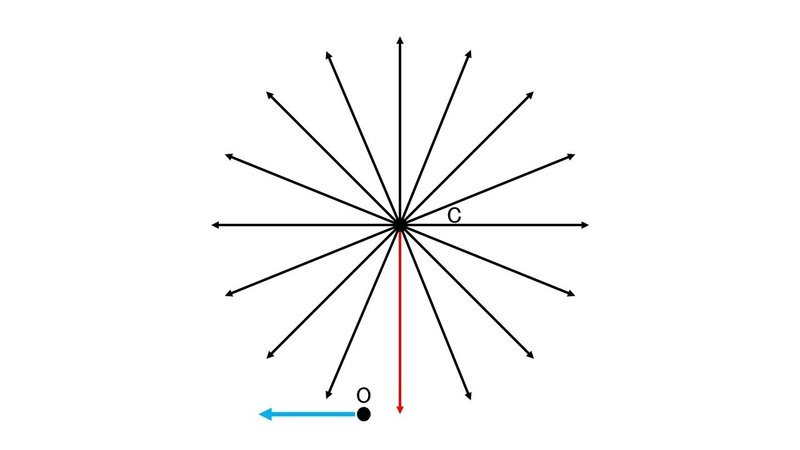
一方, 自機よりも下にあるキューブは, 自機の後方を狙って来る傾向にあることが次の図より分かる.
よって, さっきとは逆に, もし左右の動きで避けるとしたら, 自機を右に動かす必要がある.

なぜ左下のカマクラが多いのか

カマクラを作る場合, 左下に作るのが主な方法で, 次いで多いのが左上に作る方法となるのだろうが(あとの作り方は曲芸プレイ), ここまでの理屈が分かると, それがなぜなのか説明ができる.

自機が下にいるということは, 0[mino]のラインで出現した場合を除いて, キューブは自機よりも上にある.
よって, それらのキューブが自機に向かって加速した瞬間に左右にレバーを入れて避けるとなると, 大原則に照らし合わせると左に動くべきということになる.
そうすると, 安全に避けられる動きが, 画面右側から出現するキューブに対して退く動きとなり不自然さがあまりない.

一方, 自機が上にいるとき, 大原則に照らし合わせると, 左右の2択では右に動く方が安全な避け方となるが, これは右側から向かってくるキューブに対してこちらから向かって行くような動きとなり, 少し無理が生じる.

円弧を描くだけが時計回りではない

先程の図を再掲する.

この図を額面通りに受け取ると, 自機はキューブを中心として時計回りに円弧を描いて避けることになる.
それ自体は決して間違っていない. むしろ極めて正しいとすら言える.

しかし, 時計回りで動くという大原則に適う動きはこれだけではない.

近づく動きと遠ざかる動き

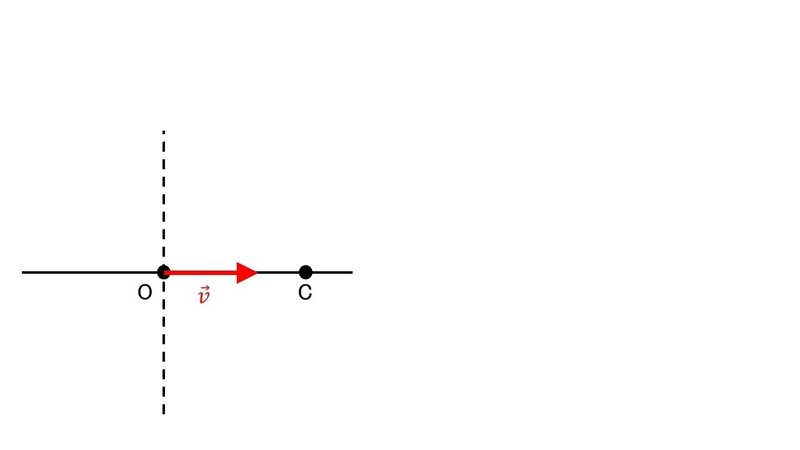
上の図において, 点O, Cはそれぞれ, キューブが自機を狙って加速する瞬間の自機の位置とキューブの位置を表している.
また, $${\vec{v}}$$(「ベクトル(vector)v」と読む)は自機の「(瞬間の)速度((instantaneous)velocity)」を表している. すなわち動く向きに矢印を描き, 時間あたりに動く距離を矢印の長さで表している. レバー入力を表していると捉えてもらうのでも構わない.

この図の場合, 自機がまっすぐにキューブに近づく動きを表している.

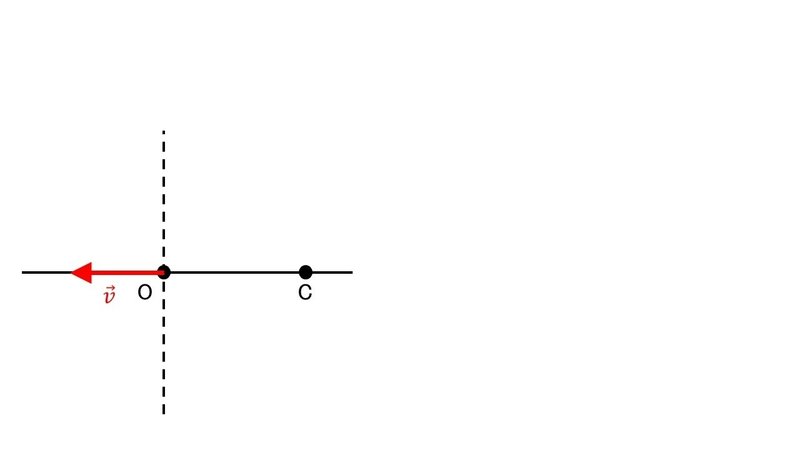
ベクトルが逆を向くと, キューブから遠ざかる動きになる.

キューブを中心とした回転

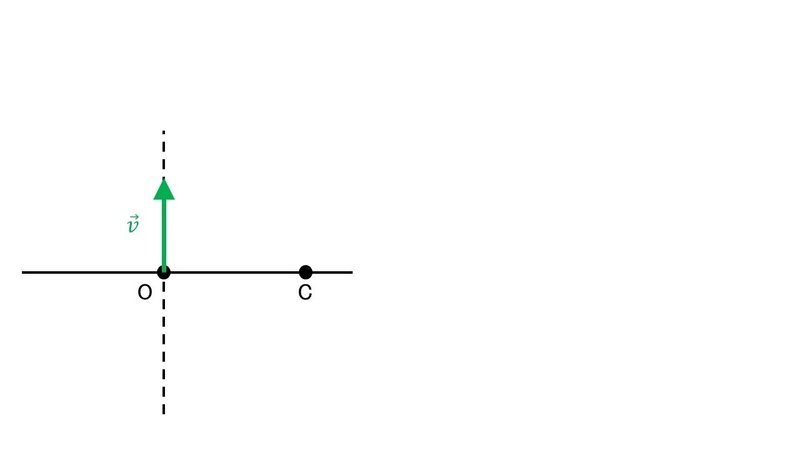
今度は, $${\vec{v}}$$が直線OCに垂直な場合を考える.

上の図は, キューブを中心として自機が時計回りに回転する動きを表している.

ベクトルは矢印であり, 円弧ではなく直線的に描かれているが, これは回転を表している.
これが回転であることは, 次のように図に少し手を加えると分かる.

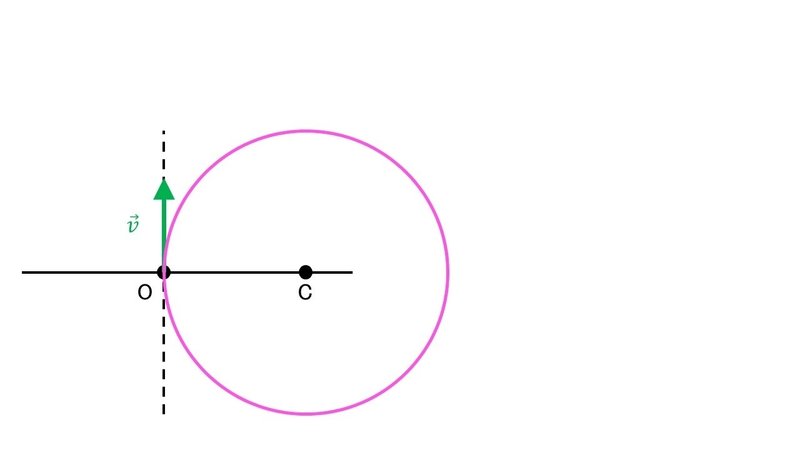
点Cを中心に, 点Oを通る円を描いた.

ここで$${\vec{v}}$$が表しているのが「瞬間の動き」, すなわち極めて短い時間の動きであることに注意してほしい.
すると, この図が表している瞬間に着目, これは点Oに極めて近い領域にだけ着目するという捉え方でもよいが, 自機が直線的に動いているのか, それとも円弧を描いて回転しているのかは, あまり区別がつかない.

よって, これはキューブを中心とした時計回りの動きを表していると考えても構わないのである.
キューブの軌道は, キューブを中心に自機から反時計回りに測って11.25°よりも小さな範囲内のどこかに存在するわけだが, 自機がキューブの軌道と交差しないということとも矛盾しない.

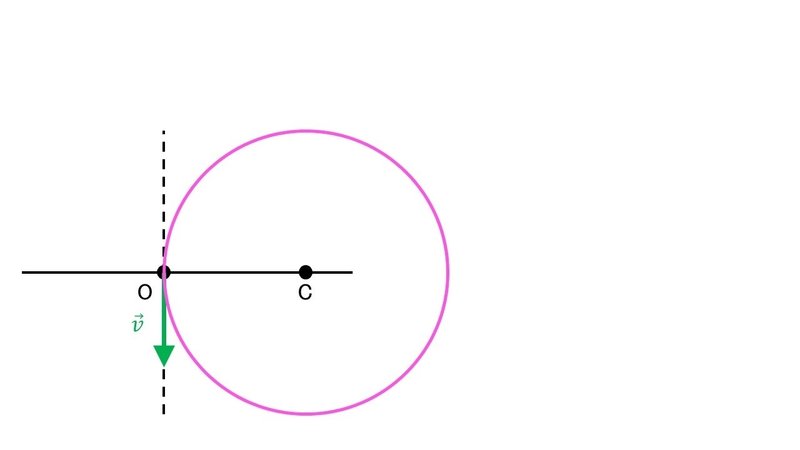
$${\vec{v}}$$が逆を向けば, 逆回転を表す.

一般の場合(2つの動きの組合せ)

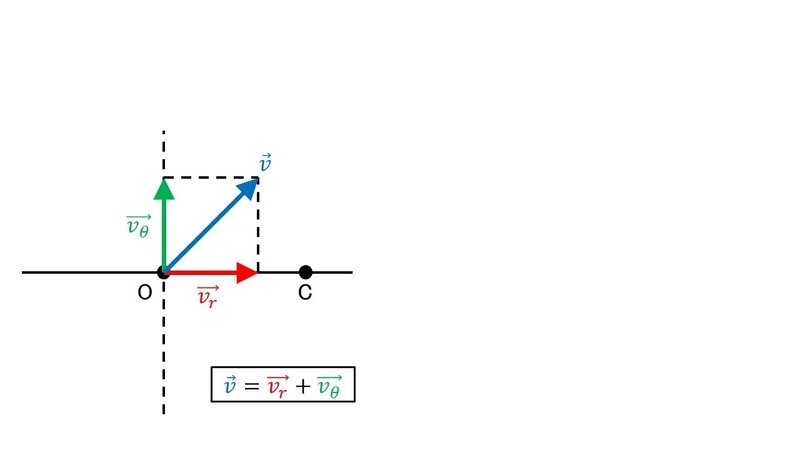
一般的には$${\vec{v}}$$の方向は直線OCと同じか垂直であるとは限らず, あらゆる向きを向く可能性がある.
その様子を表したのが上の図である.

このような場合, $${\vec{v}}$$が表す動きが直線OCに対して斜めを向いていたとしても, 直線OCと同じ方向の$${\vec{v_r}}$$という動きと, 直線OCに垂直な$${\vec{v_\theta}}$$という動きの組合せによって成り立っていると考えることができる.
$${\vec{v_r}}$$と$${\vec{v_\theta}}$$は, $${\vec{v}}$$の「影の動き」と考えるとよい.
この, 「2つの動きの組合せによって動きが成り立っている」ということを表すのが, 図中にも
$${\vec{v}=\vec{v_r}+\vec{v_\theta}}$$
と書いたような「ベクトルの加法(addition of vector)」である.

実は色々な時計回りがある(「かまぼこの定理」)

結局のところ, $${\vec{v}}$$を
$${\vec{v}=\vec{v_r}+\vec{v_\theta}}$$
のように, 2つの動きに分解(resolution)したときに, キューブを中心とした回転の向きを表す$${\vec{v_\theta}}$$が時計回りになっていれば, そのような動きは全て時計回りなのである.

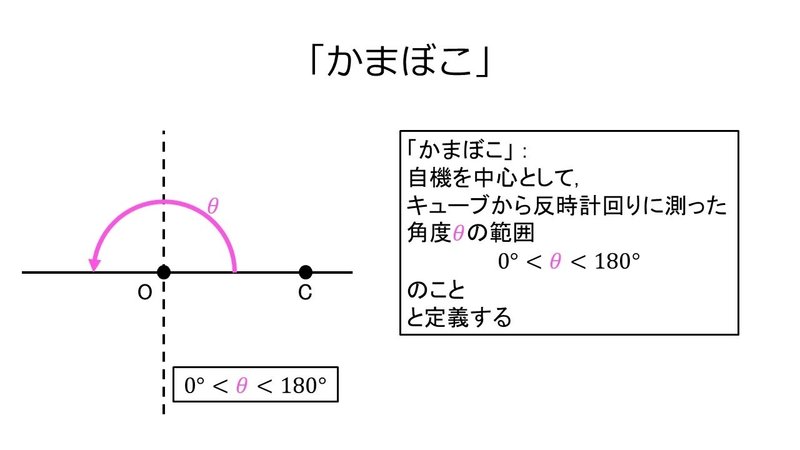
そこで, 自機を中心として, キューブから反時計回りに測った角度$${\theta}$$の範囲
$${0^\circ < \theta < 180^\circ}$$
のことを「かまぼこ(Kamaboko, steamed fish paste)」と定義し,
キューブが加速する瞬間に, かまぼこの範囲に対してレバー入力を行えばキューブを避けられる可能性が高い
という「かまぼこの定理(theorem of Kamaboko)」が導かれるのである.

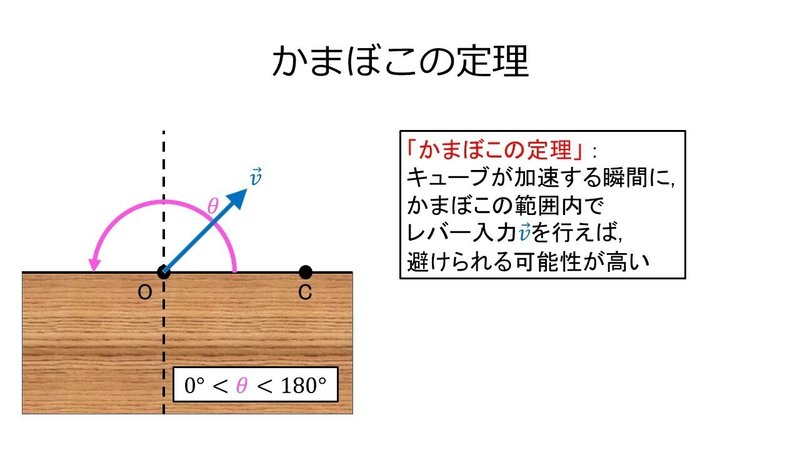
キューブを回避可能な範囲は180°「も」あって結構広いのだということは, ぜひ知ってもらいたい.

おおよそ直感では思い付かない動き

「かまぼこの定理」が理解できると, おおよそプレイしながら直感では思い付かないような動きを作ることができる.
すると, 動きのバリエーションが広がり, 使える空間が増える.

「めくり避け」

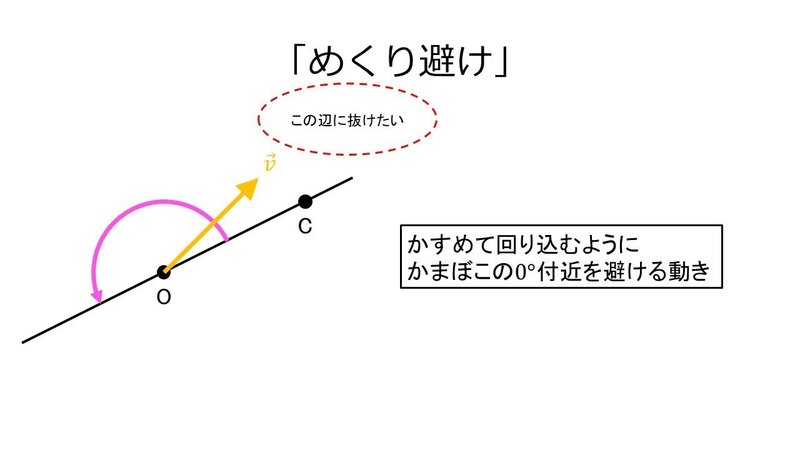
上の図のように, 自機に向かって来るキューブをかすめるようにして, かまぼこの$${0^\circ}$$付近を避ける動きのことを「めくり避け(cross up dodge)」ということにする.

この動きをすると, 元々キューブがあった位置に動いたり, その向こう側に回り込むことが可能となる.
また, コンパクトな動きなので, 画面の空間を有効に使うことができるようになる. 避けなければいけないキューブは1個ではなく次々と襲って来るので, 大きな動きでばかり避けていると端に追いやられて, その後のキューブを避けるための空間の余地が足りなくなったりするのである.

「めくり」は格闘ゲーム用語から筆者が採用した.
もちろん, キューブラッシュにはガード(とその向き)という概念は存在しないが, 相手の裏に回り込むというイメージが一致したためである.

「めくられ避け」

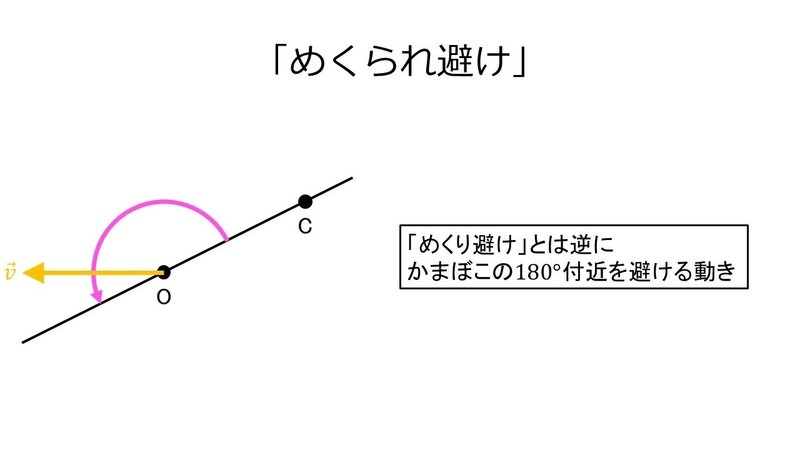
かまぼこの$${180^\circ}$$付近を避けることもできて, これを「めくられ避け(side by side dodge)」ということにする.

この動きをすると, 一瞬キューブと並走するような動きになる.
慣れないうちは, 見ていてもやっていても不思議な動きに見えるだろう.

こちらは, めくり避けと比較した場合に実行は難しいと考えられる.
なぜならば, めくり避けの場合はキューブをかすめればよいので, そのキューブを向かう地点の目標にすることができるが, こちらはそれが無いからである.

2個同時に加速するキューブへの対処

かまぼこの定理が理解できると, 2個同時に加速するキューブへの対処法も導くことができる.
キューブが同時に加速する最大の個数は2個なので, これができるようになれば, 理論上全ての場合において避けることができる.

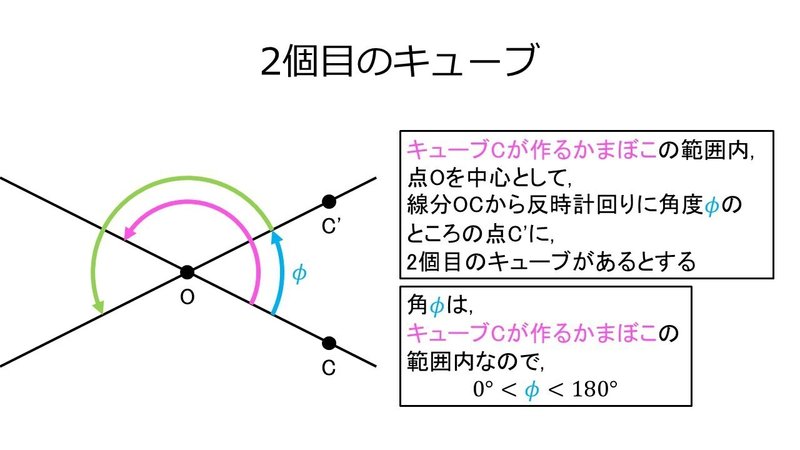
2個目のキューブの位置を点C'とする.
線分OC'は, キューブCが作るかまぼこの範囲内にあるものとし, 点Oを中心として線分OCから反時計回りに$${\phi}$$であるとする.

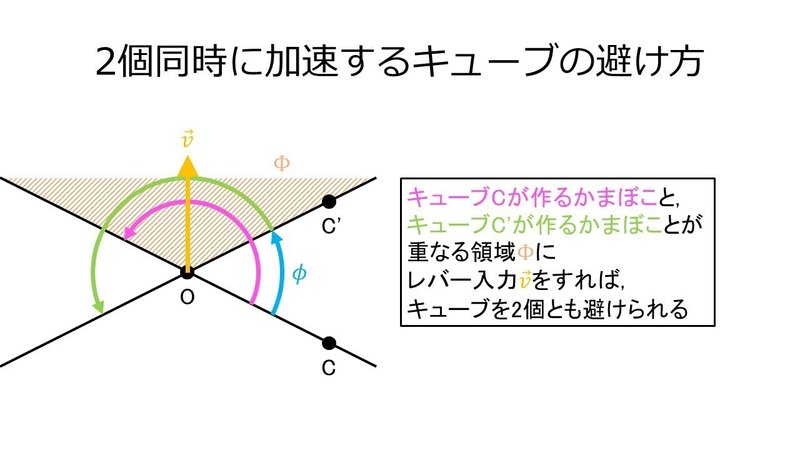
するとあとは簡単な話で, 2つのキューブが作るかまぼこが重なる領域$${\Phi}$$に避ければ, キューブを2個とも避けられるのである.

2個同時加速に対するめくり避け

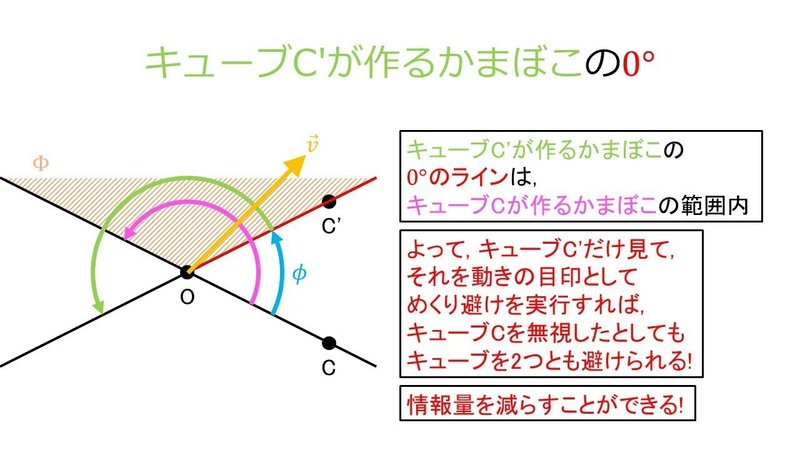
$${\Phi}$$の範囲内であればどのように避けても構わないのであるが, キューブC'に対してめくり避けをすると, キューブC'が作るかまぼこの$${0^\circ}$$のラインは, キューブCが作るかまぼこの範囲内に必ずあるので, キューブCを無視してキューブC'だけを目印に避けを実行したとしても, キューブを2個とも避けられるのである.

つまり, キューブが2個同時に加速する場面では, めくり避けは情報量を減らすのに役立つのである.

2個同時加速に対するめくられ避け

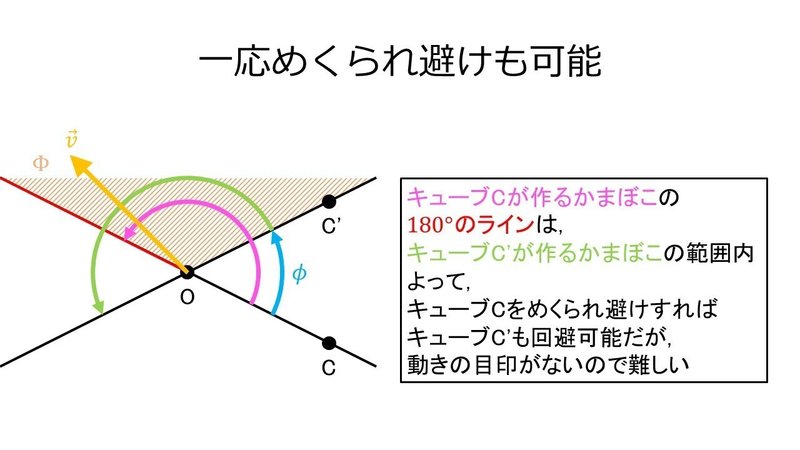
一応, めくられ避けも可能で, こちらはキューブCに対して行う.
この場合も片方のキューブを無視できるため情報量を減らすことができるが, やはりめくられ避けであるから, 動きの目印がない分めくり避けに比べて実行が難しい.

第3の避け

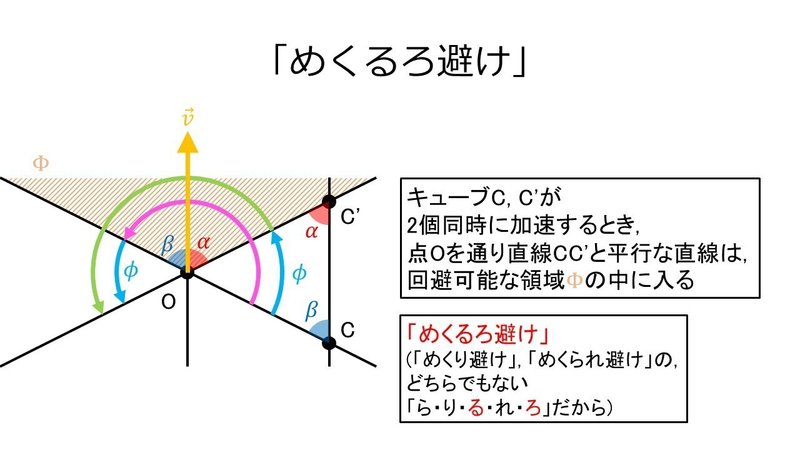
上の図では, 「対頂角(vertically opposite angle)」, 「同位角(corresponding angle(s) )」, 「錯角(alternate interior angle(s))」の性質を用いて, 大きさが等しい角を示してある.
$${\vec{v}}$$は, 2つのキューブを結んだ直線CC'と平行であるとする.

図より
$${\alpha + \beta + \phi = 180^\circ}$$
であることが分かる.
点Oに着目してもよいし, $${\triangle}$$OCC'の内角の和に着目してもよい.

すると, $${\vec{v}}$$は$${\Phi}$$の中に入るので, これも2個同時に加速するキューブを避けることができる動きである.

このような動きを「めくるろ避け(parallel dodge)」ということにする.

レバー入力は45°刻みであるから, 完全にこの図と同じように動くのは難しいことの方が多いと思われるが, 2個同時に加速するキューブが同じ高さにある場合にはすぐに威力を発揮する.
すなわち, 上にあるキューブは左に, 下にあるキューブは右に避けるという原則は, 同じ高さで出現した2個同時に加速するキューブに対しても有効ということである.

安全性の評価

加速するキューブが1個のみの場合は, 回避可能な領域$${\Phi}$$の大きさは$${180^\circ}$$あるが, キューブが2個同時に加速する場合, 1個目のキューブC, 自機, 2個目のキューブC'が作る角$${\phi}$$がこれを狭めることによって, キューブが1個のみの場合よりも避けるのを難しくさせる.
その場合, キューブの位置が同じであっても, 自機の位置が変わると$${\phi}$$, ひいては$${\Phi}$$の大きさが変わり, 回避の難しさが変化する.
ここからは座標平面を用いて, 自機を置く位置によって, 2個同時に加速するキューブに対する安全性がどのように変化するのかを示す.

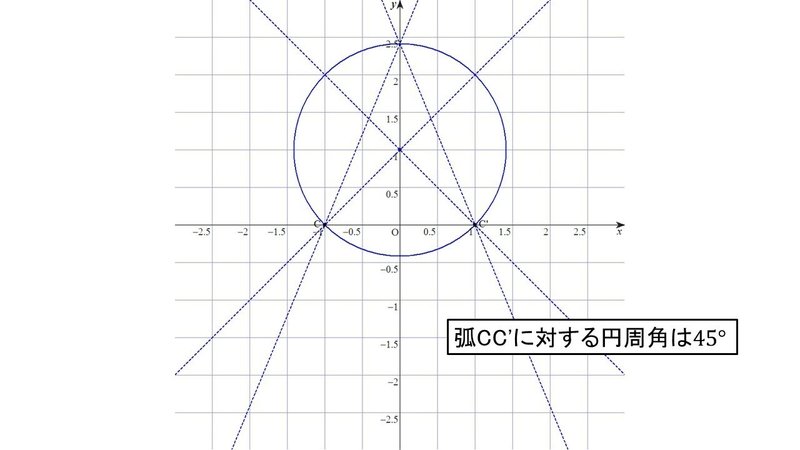
まず, 点C, C'をそれぞれ$${(-1, 0), (1, 0)}$$に配置する.
$${(0, 1)}$$を中心に, 点C, C'を通る円を描けば, $${x}$$軸より下側の弧CC'に対する中心角(central angle)は90°なので, 円周角(angle of circumference)は45°となる.

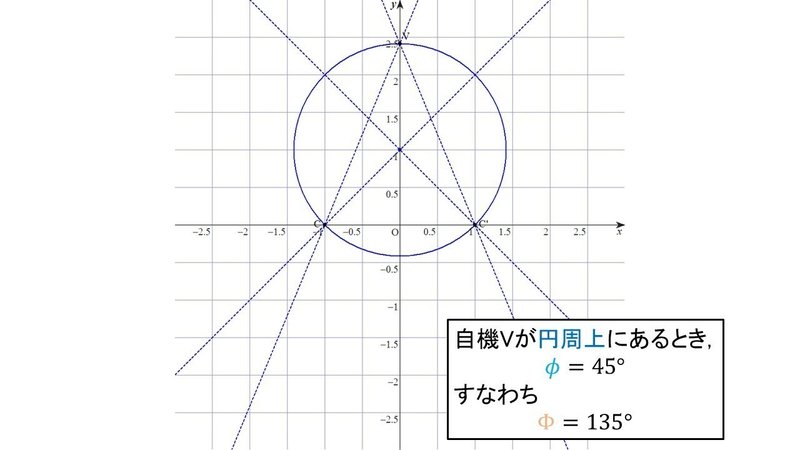
ここでの円周角は, 先程までの角度$${\phi}$$に相当し, よって, 回避可能な領域の大きさは
$${\Phi = 135^\circ}$$
となる.
座標平面の原点に「O」を取られてしまっているので, 自機の位置は点Vとしてある(「VIC VIPER」なので). 各自, 適当に読み替えてほしい.

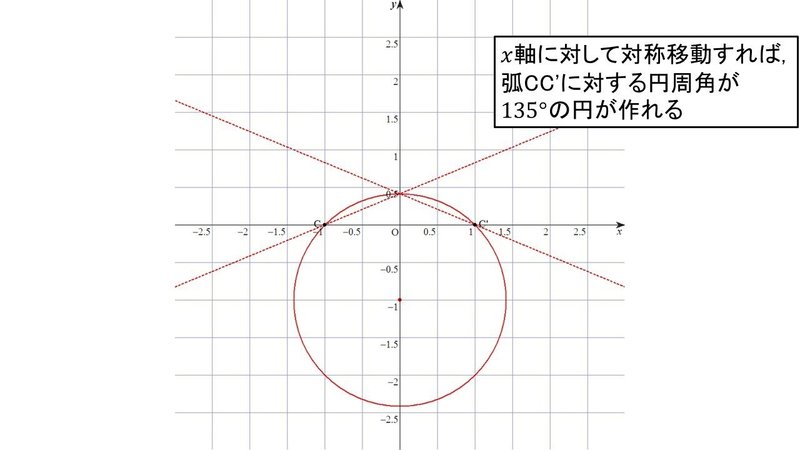
次に135°の円周角を作る.
45°の円周角を作ったときの円を$${x}$$軸に対して対称移動すればよい.
なぜならば, 円に内接する四角形の対角の和は180°だからである.

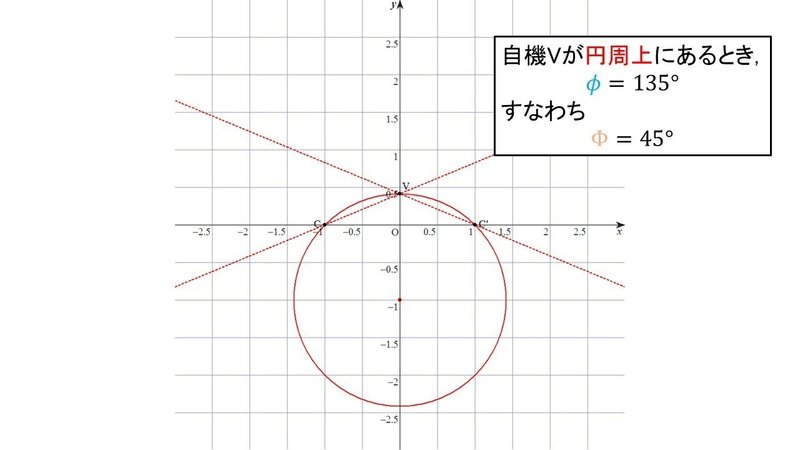
よってこの場合の回避可能な領域の大きさは
$${\Phi = 45^\circ}$$
となる.

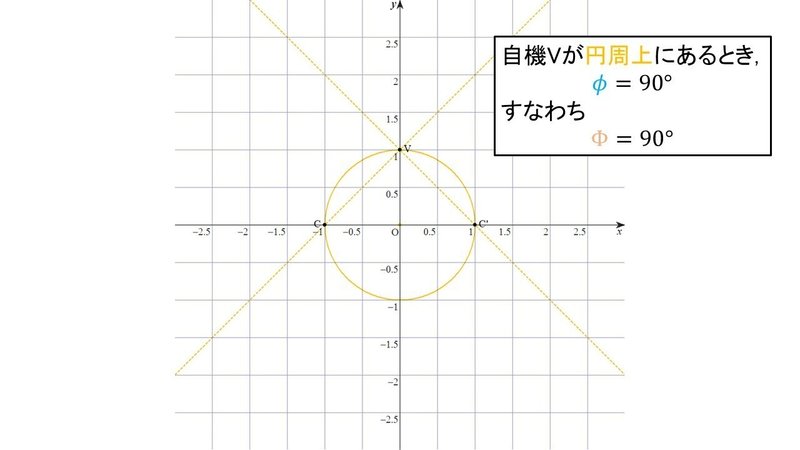
最後に, 90°の円周角を作る.
これは直径に対する円周角が90°になることを用いれば簡単に描くことができて, 原点を中心に半径が1の円を描けばよい.
この場合の回避可能な領域の大きさは
$${\Phi = 90^\circ}$$
となる.

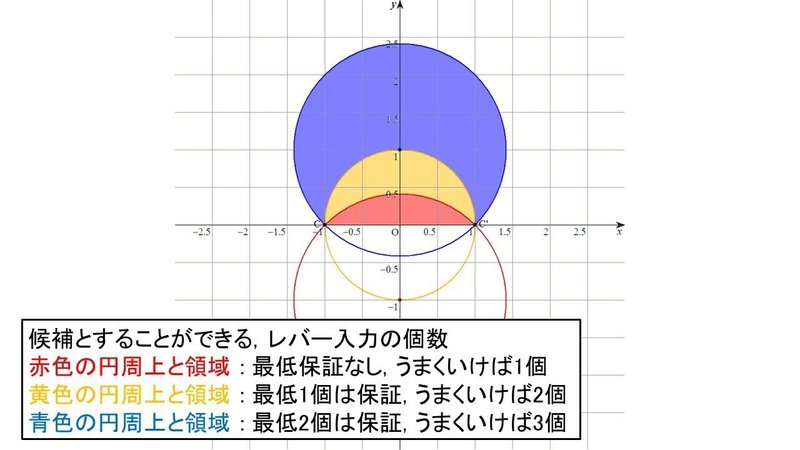
以上をまとめて, 回避可能な領域の$${\Phi}$$の大きさに応じて色分けをしたのが上の図である.
回避可能な領域の大きさとはつまり, 候補とすることができるレバー入力の個数と関連しているので, それを以って安全性の高さとしている.
これで, キューブが2個同時に加速する瞬間の自機の位置によって, 安全性がどのように変化するのかが図示できた.

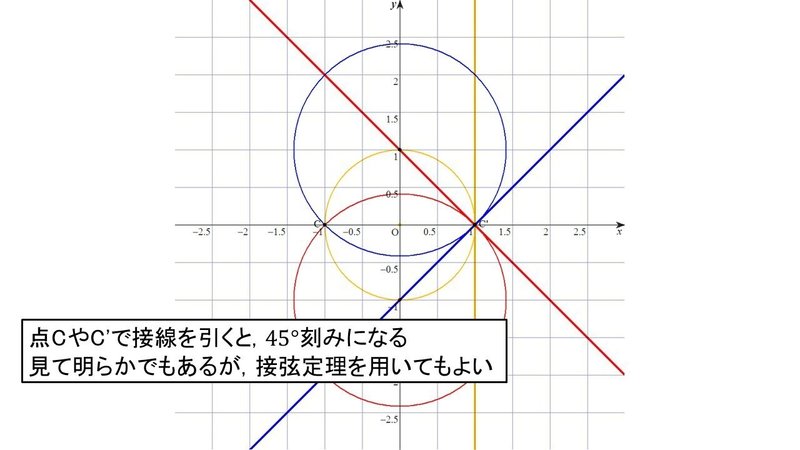
このとき, キューブの位置において, それぞれの円に対して接線を引くと, それらは45°刻みとなる.
接弦定理(alternate segment theorem)により, 接線と弦(この場合は線分CC')が作る角の大きさは, その弦が張ってある弧に対する円周角の大きさと等しいからである.

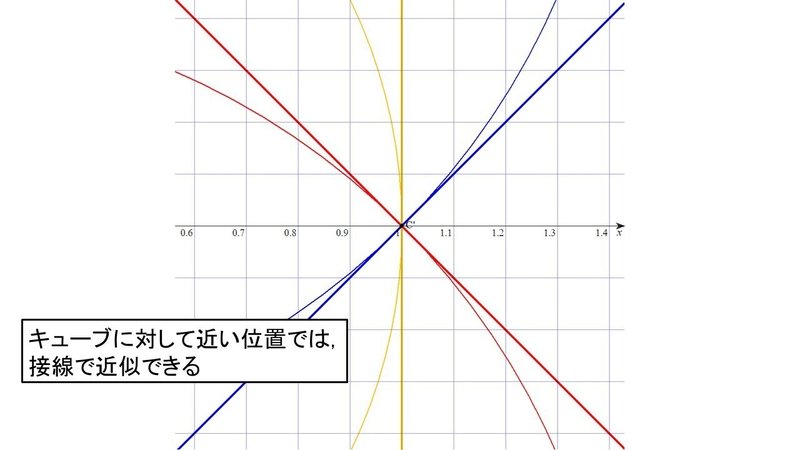
このことから, 円を描かなくても, キューブに近い位置においては, 45°刻みの接線で近似することができると分かる.

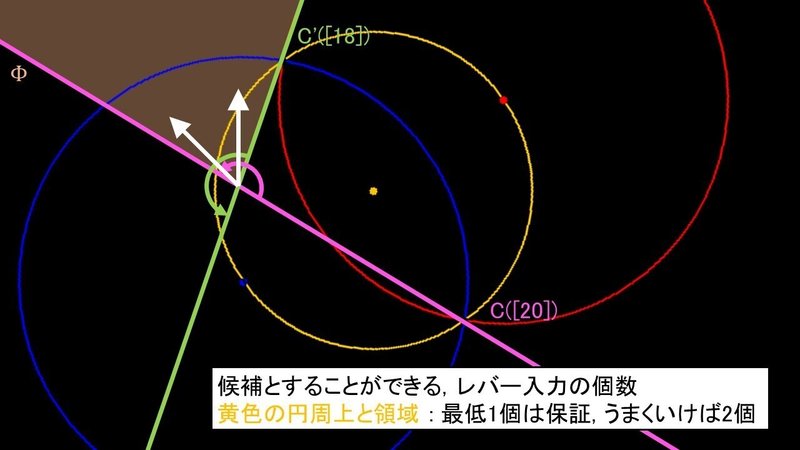
[18]と[20]の同時加速の例を示す.
上の図は[18]と[20]が加速する瞬間を表している.
この例における自機の位置は, 候補とすることができるレバー入力の個数が最低1個は保証され, うまくいけば2個存在する領域内にある.
実際, 回避可能な領域に入るレバー入力は2個存在しており, 2つのキューブが作る両方のかまぼこに入っていることが分かる.