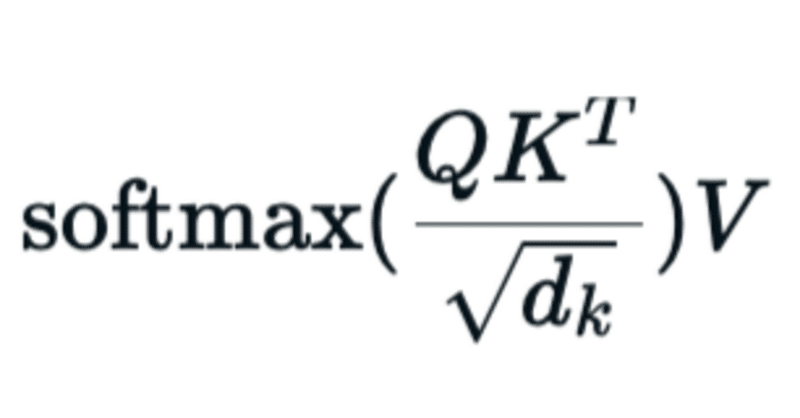
何故AttentionのSoftmaxはEmbeddingの次元数の平方根で割らなければならないのか?
$$
\text{Attention}(Q, K, V) = \text{softmax}(\dfrac{QK^T}{\sqrt{d_k}})V
$$
Why $${QK^T}$$ should be divided by $${\sqrt{d_k}}$$?
こう考えたことはないだろうか?その答えの全てはAttention is all you need.の論文に書かれている。
Scaled Dot Product Attentionの$${QK^T}$$各要素の値は行列演算の手により, 大きくなりすぎることがある, その場合Softmaxの値はGradientsの小さい領域にすぐ移動してしまい, 勾配消失という問題が起きてしまうのが主な理由である。
これはsoftmaxの図を検索して確かめて欲しい, 実際にグラフの端に近づくほど勾配は小さくなっている。これは確かに学習がうまくいかないことが予想できる。
では何故$${\sqrt{d_k}}$$で割るのだろうか, その答えは実はAttention is all you need.の原論文の下の端っこに書かれている。
原文
To illustrate why the dot products get large, assume that the components of $${q}$$ and $${k}$$ are independent random variables with mean $${0}$$ and variance $${1}$$. Then their dot product, $${q · k = \sum_{i = 1}^{d_k}q_ik_i}$$, has mean $${0}$$ and variance $${d_k}$$.
この文ではScaled Dot Product Attentionの計算結果が大きくなる理由を, $${Q, K}$$を構成する成分の数がそれぞれ平均0, 分散1の独立確率変数であることを仮定すると次元数$${d_k}$$に従って分散が大きくなることを示している。だから, $${\sqrt{d_k}}$$で割って正規化してしまおうというのが元論文の考えである。
これはあくまでも仮定なので, 本当に$${Q, K}$$の各成分が平均0, 分散1の独立確率変数に従うのかということはぶっちゃけ初期値にもよるし, 計算にもよるんじゃないかなと思いますが, 大切なのはSoftmaxの値がGradientsの小さい領域にいかず, きちんと勾配が計算されて消失しないことなので, $${\sqrt{d_k}}$$で割って上手くいったから変えていないのではないかなと思います。
この記事が気に入ったらサポートをしてみませんか?
