唐突ですが、noteで数式が使えるようになりましたね。
2021年12月なので、すごい今更ではありますが。。。

今回はnoteの数式機能をテスト的につかっていきたいと思います！

タイトルにもあるように、 $${平均継続期間 = \dfrac{1}{解約率}}$$ を解説していきたいと思います。

平均継続期間とは

サブスクリプションサービスやアプリ系では「平均継続期間」が重要です。
なぜなら、「LTV（Life Time Value）」を求めるときに使うからですね。

LTVの考え方は複数ありますが、今回は下記を採用しましょう。

$$
\bm{LTV = 顧客単価 \times 利益率 \times 平均継続期間}
$$

ご覧の通り、 $${LTV}$$ の算出に平均継続期間が必要になります。

ここでQuestionです。

$${平均継続期間 = \dfrac{1}{解約率}}$$ というのを目にしたことがある人も多いと思いますが、これは正しいのでしょうか？

結論からいうと

$$
平均継続期間 = \frac{1}{解約率}
$$

は正しい式です。（解約率が一定、という条件の下で）
今回はこれを示してみよう、というわけです。

導出（前半）

簡単な例

平均継続期間について例を使いつつ見ていきます。

あるサービスにおいてユーザーがAさんとBさんの2人だけの場合で、
Aさんが8ヶ月継続、Bさんが12ヶ月継続したとします。

このとき、平均継続期間はどうなるでしょう？
非常に単純で次のように10ヶ月になります。

$$
平均継続期間 = \frac{8 + 12}{2} = 10
$$

では、今度はユーザーがAさん、Bさん、Cさんの場合。
Aさんが9ヶ月継続、Bさんが12ヶ月継続、Cさんが15ヶ月継続ならどうでしょう？

この場合も単純で

$$
平均継続期間 = \frac{9 + 12 + 15}{3} = 12
$$

で、12ヶ月となります。

つまり、「ユーザーの延べ継続期間」を「ユーザー数」で割ったものが平均継続期間期間です。

$$
平均継続期間 = \frac{ユーザーの延べ継続期間}{ユーザー数}
$$

じゃあ「ユーザーの延べ継続期間」を求めよう

ここでは初月（1ヶ月目）のユーザー数を $${U}$$ 、月間の解約率（チャーンレート）を $${N}$$ とします。

$$
\def \arraystretch{1.5}
\begin{array}{l|c|c}
期間 & 解約数 & ユーザー数 \\ \hline
1ヶ月目 & 0 & U \\
2ヶ月目 & UN & U(1-N) \\
3ヶ月目 & U(1-N) \times N & U(1-N)^2 \\
4ヶ月目 & U(1-N)^2 \times N & U(1-N)^3 \\
5ヶ月目 & U(1-N)^3 \times N & U(1-N)^4 \\
6ヶ月目 & U(1-N)^4 \times N & U(1-N)^5 \\
7ヶ月目 & U(1-N)^5 \times N & U(1-N)^6 \\
8ヶ月目 & U(1-N)^6 \times N & U(1-N)^7 \\
9ヶ月目 & U(1-N)^7 \times N & U(1-N)^8 \\
10ヶ月目 & U(1-N)^8 \times N & U(1-N)^9 \\
11ヶ月目 & U(1-N)^9 \times N & U(1-N)^{10} \\
12ヶ月目 & U(1-N)^{10} \times N & U(1-N)^{11} \\
・・・ & ・・・ & ・・・ \\
n-1ヶ月目 & U(1-N)^{n-1} \times N & U(1-N)^{n}
\end{array}
$$

$${n-1}$$ヶ月目まで見ると上記のようになります。

最終的にユーザー数が0になるまでウォッチしていきたいと思います。
現実的には不可能ですが、数学的な問いとしては問題ないです。

少し詳しく説明すると
今、$${N}$$ は解約率なので

$$
0 \le N \le 1
$$

の範囲になります。

現実的には、解約率が $${0\%}$$ とか $${100\%}$$ というのはありえないと思うので、

$$
0 < N <1
$$

と考えてよいと思います。
このとき、

$$
\lim_{n \to \infty} (1-N)^n = 0
$$

となります。
要するにユーザー数が0になるとは、
$${\infty}$$ヶ月目まで考えよう、ということです。

つまり、こういうことですね。

$$
\def \arraystretch{1.5}
\begin{array}{l|c|c}
期間 & ユーザー数 \\ \hline
1ヶ月目 & U \\
2ヶ月目 & U(1-N) \\
3ヶ月目 & U(1-N)^2 \\
4ヶ月目 & U(1-N)^3 \\
5ヶ月目 & U(1-N)^4 \\
6ヶ月目 & U(1-N)^5 \\
7ヶ月目 & U(1-N)^6 \\
8ヶ月目 & U(1-N)^7 \\
9ヶ月目 & U(1-N)^8 \\
10ヶ月目 & U(1-N)^9 \\
11ヶ月目 & U(1-N)^{10} \\
12ヶ月目 & U(1-N)^{11} \\
13ヶ月目 & U(1-N)^{12} \\
・・・ & ・・・ \\
\infty ヶ月目 & U(1-N)^{\infty} \\
\end{array}
$$

最後のユーザー数は $${\infty-1}$$ では？と思う方もいるかもしれませんが、$${\infty}$$ も $${\infty-1}$$も変わりませんので、間違いではないです。

ピンと来る人はすぐに分かると思いますが、ピンと来ない人は理解しがたいと思うので、また簡単な例で見てみましょう。

例えば、
3ヶ月間　　 継続したユーザーが10人いて、
2ヶ月間だけ 継続したユーザーが20人いて、
1ヶ月間だけ 継続したユーザーが30人います。

と言われたら、延べ継続期間を

$$
3 \times 10 + 2 \times 20 + 1 \times 30 = 100
$$

と計算すると思います。

これは下のグラフで言うと、『縦に分割して』計算しています。

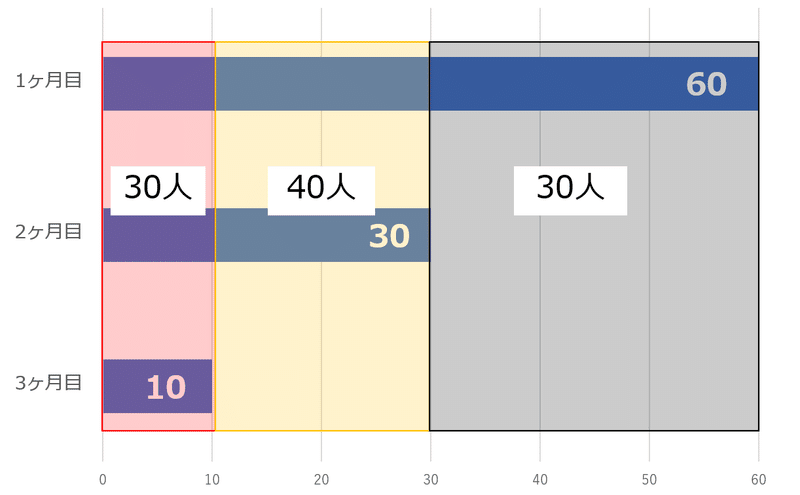
1ヶ月だけ使った人　⇒　黒枠の部分
2ヶ月だけ使った人　⇒　黄枠の部分
3ヶ月間使った人　　⇒　赤枠の部分

ここまで来たらなんとなくピンと来るでしょうか。

先程の、

3ヶ月間  継続したユーザーが10人いて、
2ヶ月間  継続したユーザーが20人いて、
1ヶ月間  継続したユーザーが30人います。

を言い換えると以下になります。
（※上のグラフもよく見て考えてみてください）

1ヶ月目にはユーザーが60人いて、
2ヶ月目にはユーザーが30人残っていて、
3ヶ月目にはユーザーが10人残っていた

さっきは、延べ継続期間を

$$
3 \times 10 + 2 \times 20 + 1 \times 30 = 100
$$

と計算しましたが、単純に『棒グラフの数値』を足せば

$$
60 + 30 + 10 =100
$$

でも求められるじゃん、ってことです。

ここまでを踏まえると、「ユーザーの延べ継続期間」が
以下の表の「ユーザー数を全て足した数（ユーザー数の総和）」になるということが分かるのではないでしょうか。

つまり、上の棒グラフのように考えると、
『グラフの数値を単に足し合わせている』ということです。

$$
\def \arraystretch{1.5}
\begin{array}{l|c|c}
期間 & ユーザー数 \\ \hline
1ヶ月目 & U \\
2ヶ月目 & U(1-N) \\
3ヶ月目 & U(1-N)^2 \\
4ヶ月目 & U(1-N)^3 \\
5ヶ月目 & U(1-N)^4 \\
6ヶ月目 & U(1-N)^5 \\
7ヶ月目 & U(1-N)^6 \\
8ヶ月目 & U(1-N)^7 \\
9ヶ月目 & U(1-N)^8 \\
10ヶ月目 & U(1-N)^9 \\
11ヶ月目 & U(1-N)^{10} \\
12ヶ月目 & U(1-N)^{11} \\
13ヶ月目 & U(1-N)^{12} \\
・・・ & ・・・ \\
\infty ヶ月目 & U(1-N)^{\infty} \\
\end{array}
$$

さて、ではユーザー数の数列を見てみる。

$$
\{U, U(1-N), U(1-N)^2, U(1-N)^3, \cdots , U(1-N)^n, \cdots \}
$$

これは高校生でも習う
$${\bm{初項がU, 公比が (1-N) の等比数列}}$$ (†)
というやつだ。

こいつらの和を考えろというが問題であり、
ガッツリ数式で書くと

$$
\sum_{n=0}^{\infty} U(1-N)^n = \lim_{n \to \infty} \sum_{k=0}^n U(1-N)^k
$$

ということですね。

ここまでが前半です。
ここで少し等比数列の復習をするので、分かっている人は飛ばしてください。

等比数列の復習

等比数列の総和

$${初項a, 公比r の等比数列}$$を$${第n番目}$$まで書くと次のようになります。

$$
\{a, ar, ar^2, ar^3, ar^4, \cdots, ar^{n-1} \}
$$

要するに、最初の項が「$${a}$$」で、それ以降は「$${r 倍}$$されていく数列になります。

これらの和は

$$
S_n = \frac{a\left(1-r^n \right)}{1-r}
$$

になります。

簡単に証明してみましょう。
まず単純に「和」なので全部足してみると

$$
S_n = a + ar + ar^2 + ar^3 + ar^4 + \cdots + ar^{n-3} + ar^{n-2} + ar^{n-1}
$$

と書けます。（☆）
この両辺を$${r 倍}$$してあげると

$$
r \times S_n = ar + ar^2 + ar^3 + ar^4 + \cdots + ar^{n-3} + ar^{n-2} + ar^{n-1} + ar^n
$$

となります。

上の式から下の式を引くと、等しいところは相殺して消えるので、

$$
\begin{aligned}
S_n &= a +\cancel{ar} + \cancel{ar^2} + \cancel{ar^3} + \cancel{ar^4} + \cdots + \cancel{ar^{n-3}} + \cancel{ar^{n-2}} + \cancel{ar^{n-1}} \\
r \times S_n &= \cancel{ar} + \cancel{ar^2} + \cancel{ar^3} + \cancel{ar^4} + \cdots + \cancel{ar^{n-3}} + \cancel{ar^{n-2}} + \cancel{ar^{n-1}} + ar^n \\
(1-r)S_n &= a-ar^n = a \left(1-r^n \right)
\end{aligned}
$$

となります。

よって、$${rが1以外}$$であれば、
最後の式の両辺を$${1-r}$$で割って

$$
S_n = \frac{a \left(1-r^n \right)}{1-r}
$$

ということになります。（♡)

$${r=1}$$ならもっと単純で、（☆）の式を見れば

$$
\begin{aligned}
S_n &= a + ar + ar^2 + ar^3 + ar^4 + \cdots + ar^{n-3} + ar^{n-2} + ar^{n-1}\\
&= a + a+ a +a +a +\cdots +a + a + a  \ (aをn個足す)\\
&=na
\end{aligned}
$$

になります。

さらに、

$$
-1 < r < 1
$$

であるなら

$$
\lim_{n \to \infty} r^n = 0
$$

となるため、

$$
\begin{aligned}
\lim_{n \to \infty} S_n &= \lim_{n \to \infty}  \frac{a \left(1-r^n \right)}{1-r}\\
&= \frac{a}{1-r}
\end{aligned}
$$

に収束することが分かります。(♡♡)

(♡)の$${nを\infty}$$にするということは、
つまり(☆)の式で$${n}$$をどんどん大きくして無限まで足していくことです。

その総和が(♡♡)に収束すると言っています。

導出（後半）～話を延べユーザー継続期間へ～

ユーザー数を全て足した数（ユーザー数の総和）を求めよう

話を元に戻しましょう。

今の証明で「初項$${a}$$、公比$${r \ (-1 < r <1)}$$」の等比数列を無限に足していくと

$$
\lim_{n \to \infty}S_n = \frac{a}{1-r}
$$

に収束するのでした。

数学的には(†)にも記載した通り
『$${\bm{初項がU、公比が (1-N) の等比数列}}$$』の和  (††)
でしたね。

ここで、$${N}$$は前述したように

$$
0 < N < 1
$$

と考えてよいので、$${1-N}$$ の範囲は

$$
0 < 1-N < 1
$$

となります。

よって(††)の和は収束します。

分かりづらい方は
「初項$${a}$$、公比$${r \ (-1 < r <1)}$$」の等比数列の和が

$$
\lim_{n \to \infty}S_n = \frac{a}{1-r}
$$

に収束するという話で、
$${aをU, rを(1-N)}$$に置き換えたと思ってください。

そうすると、(††)は

$$
\begin{aligned}
\lim_{n \to \infty}S_n &= \frac{U}{1-(1-N)} \\
&= \frac{U}{N}
\end{aligned}
$$

となりました。
すーごいキレイな形に収束しましたね！！

つまり

$$
ユーザーの延べ継続期間 = \frac{U}{N}= \frac{ユーザー数}{解約率}
$$

ということですね。

さて、随分前のことで忘れているかもしれませんが、
求める式は

$$
\bm{平均継続期間 = \frac{ユーザーの延べ継続期間}{ユーザー数}}
$$

ですので、

$$
\bm{
\begin{aligned}
平均継続期間 &= ユーザーの延べ継続期間 \times \frac{1}{ユーザー数}\\
&= \frac{\cancel{ユーザー数}}{解約率} \times  \frac{1}{\cancel{ユーザー数}}\\
& = \frac{1}{解約率}
\end{aligned}
}
$$

というわけです。
1行目から2行目の式変形で、先程導出した

$$
ユーザーの延べ継続期間 = \frac{U}{N} = \frac{ユーザー数}{解約率}
$$

を利用しました。

これで、無事に

$$
\bm{{平均継続期間} = \frac{1}{解約率}}
$$

が示されました。

今回はここまでです。

Bye,Bye.

広告運用に関して詳しくお話を聞きたいという企業様がいらっしゃいましたら、こちらからお問い合わせをお願い致します。

もし、私たちの会社で働く事に少しでも興味を持っていただけたら、ぜひ応募フォームよりご連絡ください。