統計的仮説検定のトピック「２種類の過誤」の確率を深掘りします。
難解な問題文章をグラフで紐解いて、第１種の過誤＆第２種の過誤の確率に近づいて行きましょう！

公式問題集の準備

「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください！
「知る」「実践する」の章で、のんびり統計をお楽しみください！

問題を解いて、知る

今回の記事の構成

この記事は、通常の記事構成と違う章立てにいたします。
「問題を解く」「知る」「実践する」を１つの章にまとめます。
Pythonによるグラフを用いて、問題の直観的な理解に全集中します！

📘公式問題集のカテゴリ

検定の分野
問10 $${(\beta, 1-\alpha)}$$のグラフ（データ例無し）

試験実施年月
統計検定2級 2019年6月 問16（回答番号29）

📕公式テキスト：7.2.1 検出力と検出力関数（215ページ～）

問題

公式問題集をご参照ください。

解き方

題意
与えられた帰無仮説と対立仮説に基づいて棄却限界値$${x_0}$$の値を変化させたとき、「第１種の過誤の確率$${\alpha(x_0)}$$を１から引いた$${1-\alpha(x_0)}$$」と「第２種の過誤$${\beta(x_0)}$$の確率」をグラフ化します。

文章や数式だけだと、問題の意味がスッと入ってこない感じがします。

第１種の過誤・第２種の過誤

統計的仮説検定の手続きで誤った仮説を採択することを「過誤」と呼びます。
帰無仮説が正しいときに帰無仮説を棄却する過誤が「第１種の過誤」であり、第１種の過誤の確率を$${\alpha}$$で表します。
対立仮説が正しいときに帰無仮説を受容する過誤が「第２種の過誤」であり、第２種の過誤の確率を$${\beta}$$で表します。

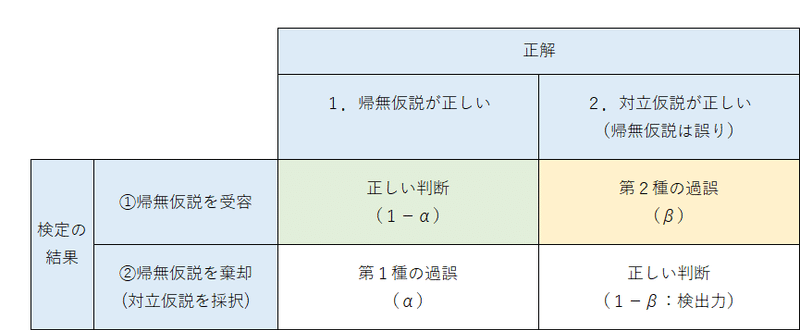
この問題では、緑色の$${1-\alpha}$$と黄色の$${\beta}$$を求めます。
統計的仮説検定の結果、帰無仮説を受容する場合において
・「帰無仮説が正しい」確率が緑色の$${1-\alpha}$$です。
・「対立仮説が正しい」確率が黄色の$${\beta}$$です。

この過誤の表を見ていると、機械学習の分類タスクの評価指標を連想します。
過誤と評価指標はおおよそ、次のような関係になるそうです。

問題文章の解読

なにはともあれ可視化して、問題の意図を掴みましょう！

確率変数$${X}$$が従う正規分布$${N(\theta, 1)}$$について、
①帰無仮説$${H_0: \theta=0}$$が正しいと仮定する場合
②対立仮説$${H_1:\theta=1}$$が正しいと仮定する場合
の２ケースで、確率密度関数を描画します。

①の帰無仮説は標準正規分布$${N(0,1)}$$です。
横軸は$${x}$$であり、目盛りの０～１を$${x_0}$$が動きます。
赤い点線は$${x_0=0.5}$$の例です。

最右側では、帰無仮説と対立仮説を１つのグラフで表現しました。
対立仮説の下の正規分布$${N(1,1)}$$は、帰無仮説の下の標準正規分布を右に１ずらしたものであることが分かります。

塗りつぶしした領域に注目してください。
この領域は過誤の確率を示しています。
では、過誤の確率を詳しく見ていきましょう！

第１種の過誤の確率$${\boldsymbol{\alpha(x_0)}}$$の可視化

棄却域を$${x \geq x_0}$$とするときの$${\alpha(x_0)}$$を描画します。
青色の領域＝面積＝確率が$${\alpha(x_0)}$$です。
なぜなら、棄却域は$${x}$$が$${x_0}$$以上のときですから、赤い点線の$${x_0}$$の右側が棄却域なのです。

左のグラフに注目します。
帰無仮説は平均が０なので、$${x_0=0}$$のとき、平均の位置、つまりど真ん中です。
このとき、$${\alpha(x_0=0)}$$である青色の領域は、正規分布のベル型のちょうど半分なので、確率は$${0.5}$$です。

右のグラフに注目します。
$${x_0}$$が$${1}$$に移動すると、青色の領域が小さくなっています。
つまり、$${\alpha(x_0=0)}$$と比べて、$${\alpha(x_0=1)}$$は減少しています。
$${x_0}$$が$${0}$$から$${1}$$へ移動するにつれて、$${\alpha(x_0)}$$は小さくなります。

$${\boldsymbol{1-\alpha(x_0)}}$$の可視化

続いて、$${1-\alpha(x_0)}$$を確認しましょう。
緑色の領域＝面積＝確率が$${1-\alpha(x_0)}$$です。
先程の$${\alpha(x_0)}$$の反対側の領域に相当するのです！

左のグラフに注目します。
帰無仮説は平均が０なので、$${x_0=0}$$のとき、平均の位置、つまりど真ん中です。
このとき、$${1-\alpha(x_0=0)}$$である緑色の領域は、正規分布のベル型のちょうど半分なので、確率は$${0.5}$$です。

右のグラフに注目します。
$${x_0}$$が$${1}$$に移動すると、緑色の領域が大きくなっています。
つまり、$${1-\alpha(x_0=0)}$$と比べて、$${1-\alpha(x_0=1)}$$は増加しています。
$${x_0}$$が$${0}$$から$${1}$$へ移動するにつれて、$${1-\alpha(x_0)}$$は大きくなります。

第２種の過誤の確率$${\boldsymbol{\beta(x_0)}}$$の可視化

続いて$${\beta(x_0)}$$を描画します。

左のグラフに注目します。
オレンジ色の領域＝面積＝確率が$${\beta(x_0)}$$です。

右のグラフに注目します。
対立仮説は平均が１なので、$${x_0=1}$$のとき、平均の位置、つまりど真ん中です。
このとき、$${\beta(x_0=1)}$$であるオレンジ色の領域は、正規分布のベル型のちょうど半分なので、確率は$${0.5}$$です。
また、$${x_0}$$が$${1}$$に移動すると、オレンジ色の領域が大きくなっています。
つまり、$${\beta(x_0=0)}$$と比べて、$${\beta(x_0=1)}$$は増加しています。
$${x_0}$$が$${0}$$から$${1}$$へ移動するにつれて、$${\beta(x_0)}$$は大きくなります。

中間まとめ

$${x_0}$$を０から１へ動かしたとき、下のグラフの横軸$${\beta(x_0)}$$と縦軸$${1-\alpha(x_0)}$$の様子について、いままでに分かったことをまとめます。

■ 横軸$${\beta(x_0)}$$について

• $${x_0=0}$$のとき、$${\beta(x_0=0)}$$は$${\beta(x_0=1)}$$より小さいです。

• $${x_0=1}$$のとき、$${\beta(x_0=1)}$$は$${0.5}$$です。

■ 縦軸$${1-\alpha(x_0)}$$について

• $${x_0=0}$$のとき、$${1-\alpha(x_0=0)}$$は$${0.5}$$です。

• $${x_0=1}$$のとき、$${1-\alpha(x_0=1)}$$は$${1-\alpha(x_0=0)}$$より大きいです。

表にします。

$$
\begin{array}{c:ccc}
x_0&0&0.5&1 \\
\hline
\beta(x_0) & <0.5? & ? & 0.5 \\
1-\alpha(x_0) & 0.5 & ? & >0.5? \\
\end{array}
$$

$${\boldsymbol{\beta(x_0)}}$$の計算

$${x_0=0}$$と$${x_0=0.5}$$のときの$${\beta(x_0)}$$を計算しましょう。
$${\beta(x_0)}$$は対立仮説の下の正規分布$${N(1,1)}$$について、$${x_0}$$の左側＝下側確率です。
つまり、確率$${P(X<0)}$$と$${P(X<0.5)}$$を計算します。

確率変数を標準化してパーセント点を求めて、標準正規分布の上側確率表を参照して確率を取得します。
標準化とは、確率変数$${X}$$、平均$${\mu}$$、標準偏差$${\sigma}$$を用いて、$${Z=\cfrac{X-\mu}{\sigma}}$$とすることです。
対立仮説の下の正規分布$${N(1, 1)}$$について、平均は$${1}$$、標準偏差は$${\sqrt{1}=1}$$です。

①確率$${P(X<0)}$$

$$
\begin{align*}
P(X<0)&=P\left(\cfrac{X-\mu}{\sigma} <\cfrac{0-\mu}{\sigma}\right) \\
 \\
&=P\left(Z <\cfrac{0-1}{1}\right) \\
 \\
&=P\left(Z <-1\right) \\
 \\
&=P\left(Z >1\right) \quad (*) \\
\end{align*}
$$

(*)$${x=-1}$$の下側確率と、$${x=1}$$の上側確率は等しいです。

$${P(Z >1)}$$は、標準正規分布の上側確率のパーセント点$${u=1}$$を参照して確率を取得できます。

$${P(X<0)＝P(Z >1)}$$は$${0.1587}$$です。

②$${P(X<0.5)}$$

同様に、$${P(X<0.5)}$$を計算しましょう。

$$
\begin{align*}
P(X<0.5)&=P\left(\cfrac{X-\mu}{\sigma} <\cfrac{0.5-\mu}{\sigma}\right) \\
 \\
&=P\left(Z <\cfrac{0.5-1}{1}\right) \\
 \\
&=P\left(Z <-0.5\right) \\
 \\
&=P\left(Z >0.5\right)  \\
\end{align*}
$$

標準正規分布の上側確率のパーセント点$${u=0.5}$$を参照して確率を取得しましょう。

$${P(X<0.5)=P(Z >0.5)}$$は$${0.3085}$$です。

表に記録しましょう。

$$
\begin{array}{c:ccc}
x_0&0&0.5&1 \\
\hline
\beta(x_0) & 0.1587 & 0.3085 & 0.5 \\
1-\alpha(x_0) & 0.5 & ? & >0.5? \\
\end{array}
$$

$${\boldsymbol{1-\alpha(x_0)}}$$の計算

$${x_0=0.5}$$と$${x_0=1}$$のときの$${1-\alpha(x_0)}$$を計算しましょう。
$${1-\alpha(x_0)}$$は帰無仮説の下の正規分布$${N(0,1)}$$、すなわち標準正規分布について、$${x_0}$$の左側＝下側確率です。

①確率$${P(X<0.5)}$$

帰無仮説の下で$${X}$$は標準正規分布に従うので、$${P(X<0.5)=P(Z<0.5)}$$です。
下側確率$${P(Z<0.5)}$$は、$${1}$$から上側確率$${P(Z>0.5)}$$を差し引いた$${1-P(Z>0.5)}$$と等しいです。
そこで、標準正規分布の上側確率表より$${P(Z>0.5)}$$を取得して、$${1}$$から引きましょう。

$${P(Z>0.5)=0.3085}$$です。
したがって、$${P(X<0.5)=1-P(Z>0.5)=1-0.3085=0.6915}$$です。

②確率$${P(X<1)}$$

$${P(X<1)=P(Z<1)=1-P(Z>1)}$$です。
標準正規分布の上側確率表より$${P(Z>1)}$$を取得して、$${1}$$から引きましょう。

$${P(Z>1)=0.1587}$$です。
したがって、$${P(X<1)=1-P(Z>1)=1-0.1587=0.8413}$$です。

表に記録しましょう。

$$
\begin{array}{c:ccc}
x_0&0&0.5&1 \\
\hline
\beta(x_0) & 0.1587 & 0.3085 & 0.5 \\
1-\alpha(x_0) & 0.5 & 0.6915 & 0.8413 \\
\end{array}
$$

表の情報に基づいてグラフを描画する

解答に近づいてまいりました。
表の$${\beta(x_0)}$$と$${1-\alpha(x_0)}$$をグラフに描画しましょう。

グラフは右肩上がりです。
ただし一直線ではなくて、上方向に出っ張った形状になっています。
解答選択肢の中で、右肩上がりで上方向に出っ張った形状のグラフは ① です。

最後に$${(\beta, 1-\alpha)}$$のグラフを描画します。
オレンジの点線は両端を結ぶ直線です。

解答

① です。

難易度　ややむずかしい

・知識：第１種の過誤、第２種の過誤、標準化、標準正規分布の上側確率表
・計算力：数式組み立て（中）、電卓（低）
・時間目安：2分
※出題の意図を理解して解答の筋道を立てることの難易度が高めです。

実践する

記事で使用したPythonの作図コードを確認しましょう。

Pythonで作成してみよう！

正規分布の確率密度関数、グラフの塗りつぶし、グラフのテキスト表示などに注目して見ていきましょう。

①インポート

### インポート
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'

②グラフ枠の描画
データ点が無くてもグラフを描けます！

### 解答を記入する白いキャンバス

plt.figure(figsize=(3,3))
plt.xlabel(r'$\beta(x_0)$', fontsize=14)
plt.ylabel(r'$1-\alpha(x_0)$', fontsize=14)
plt.xticks([]); plt.yticks([])
plt.title('$x_0$を0から1に動かしたときの\n'
          r'($\beta(x_0), 1-\alpha(x_0)$)をプロットする')
plt.show()

③帰無仮説H0と対立仮説H1の正規分布のオブジェクトの生成
H0は標準正規分布のオブジェクト、H1は正規分布$${N(1,1)}$$のオブジェクトです。
以後の処理で、H0・H1の正規分布の処理を呼び出すときに重宝します。

### 帰無仮説H0と対立仮説H1の確率分布のオブジェクトを生成

H0 = stats.norm(loc=0, scale=1)  # 平均loc=0, 標準偏差scale=1
H1 = stats.norm(loc=1, scale=1)  # 平均loc=1, 標準偏差scale=1

④帰無仮説と対立仮説の下の２つの正規分布の確率密度関数をプロット
棄却域の塗りつぶし用のデータ（例えば x1, y1_H0 ）を１つ１つ生成して、プロット時に fill_between の塗りつぶし処理で利用します。
少々冗長ですが良しとしましょう。

### 帰無仮説H0と対立仮説H1の可視化

# 棄却限界値
critical_value = 0.5

## H0とH1の正規分布の確率密度関数を取得
x = np.linspace(-5, 5, 1001)
y_H0 = H0.pdf(x)
y_H1 = H1.pdf(x)

### プロット
fig, ax = plt.subplots(1,3, figsize=(10, 3), sharex=True, sharey=True)

## H0の分布、棄却域、αのプロット
# 棄却域塗りつぶし用
x1 = np.linspace(critical_value, 5, 101)
y1_H0 = H0.pdf(x1)
# プロット
ax[0].plot(x, y_H0, color='steelblue', label='$H_0$')
ax[0].fill_between(x1, y1_H0, 0, color='steelblue', alpha=0.3, label=r'$\alpha(x_0)$')
ax[0].axvline(critical_value, ls='--', color='red', label='$x_0$')
ax[0].axhline(0, lw=0.5, ls='--', color='black')
ax[0].set_xticks([0,1])
ax[0].set_xlabel('$x$')
ax[0].set_title('①帰無仮説 $H_0:\\theta=0$\n$X \sim N(0,1)$')
ax[0].legend(loc='upper left')

## H1の分布、棄却域、βのプロット
# 第２種の過誤塗りつぶし用
x2 = np.linspace(-5, critical_value, 101)
y2_H1 = H1.pdf(x2)
# プロット
ax[1].plot(x, y_H1, color='orange', label='$H_1$')
ax[1].fill_between(x2, y2_H1, 0, color='orange', alpha=0.3, label=r'$\beta(x_0)$')
ax[1].axvline(critical_value, ls='--', color='red', label='$x_0$')
ax[1].axhline(0, lw=0.5, ls='--', color='black')
ax[1].set_xlabel('$x$')
ax[1].set_title('②対立仮説 $H_1:\\theta=1$\n$X \sim N(1,1)$')
ax[1].legend(loc='upper left')

## H0の分布、H1の分布、棄却限界値のプロット
ax[2].plot(x, y_H0, color='steelblue', label='$H_0$')
ax[2].plot(x, y_H1, color='orange', label='$H_1$')
ax[2].axvline(critical_value, ls='--', color='red', label='$x_0$')
ax[2].axhline(0, lw=0.5, ls='--', color='black')
ax[2].set_xlabel('$x$')
ax[2].set_title('$H_0, H_1$を１つのグラフで描画')
ax[2].legend(loc='upper left')

plt.show()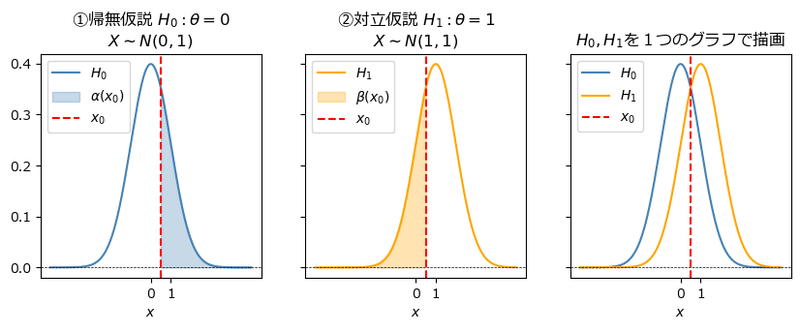

⑤$${\boldsymbol{\alpha(x_0)}}$$の可視化
④のコードをコピーしてたたき台にしています。

### α(x0)の可視化

### 設定
# x0 : 0から1へ動く
x0 = [0, 1] 

### プロット
fig, ax = plt.subplots(1,2, figsize=(10, 3), sharex=True, sharey=True)

## H0の分布、棄却域、α(x0)のプロット
# 棄却域塗りつぶし用
x1 = np.linspace(x0[0], 5, 101)
y1_H0 = H0.pdf(x1)
x2 = np.linspace(x0[1], 5, 101)
y2_H0 = H0.pdf(x2)

# x0=0のときの第１種の過誤の確率α(x0)のプロット
ax[0].plot(x, y_H0, color='steelblue', label='$H_0$')
ax[0].fill_between(x1, y1_H0, 0, color='steelblue', alpha=0.3, label=r'$\alpha(x_0)$')
ax[0].axvline(x0[0], ls='--', color='red', label='$x_0$')
ax[0].axhline(0, lw=0.5, ls='--', color='black')
ax[0].set_xticks([0, 1])
ax[0].set_xlabel('$x$')
ax[0].set_title('帰無仮説 $H_0:\\theta=0$\n$X \sim N(0,1)$')
ax[0].legend(loc='upper left')

# x0=1のときの第１種の過誤の確率α(x0)のプロット
ax[1].plot(x, y_H0, color='steelblue', label='$H_0$')
ax[1].fill_between(x2, y2_H0, 0, color='steelblue', alpha=0.3, label=r'$\alpha(x_0)$')
ax[1].axvline(x0[1], ls='--', color='red', label='$x_0$')
ax[1].axhline(0, lw=0.5, ls='--', color='black')
ax[1].set_xticks([0, 1])
ax[1].set_xlabel('$x$')
ax[1].set_title('帰無仮説 $H_0:\\theta=0$\n$X \sim N(0,1)$')
ax[1].legend(loc='upper left')

plt.show()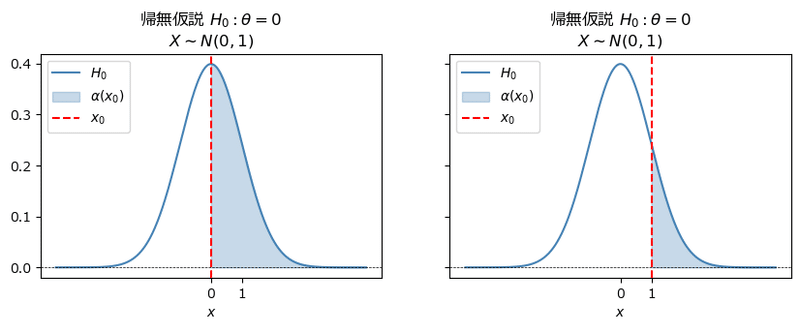

⑥$${\boldsymbol{1-\alpha(x_0)}}$$の可視化
⑤のコードをコピーしてたたき台にしています。

### 1-α(x0)の可視化

### プロット
fig, ax = plt.subplots(1,2, figsize=(10, 3), sharex=True, sharey=True)

## H0の分布、棄却域、1-α(x0)の値のプロット
# 棄却域塗りつぶし用
x3 = np.linspace(-5, x0[0], 101)
y3_H0 = H0.pdf(x3)
x4 = np.linspace(-5, x0[1], 101)
y4_H0 = H0.pdf(x4)

# x0=0のときの1-α(x0)の確率
ax[0].plot(x, y_H0, color='steelblue', label='$H_0$')
ax[0].fill_between(x3, y3_H0, 0, color='green', alpha=0.3, label=r'$1-\alpha(x_0)$')
ax[0].axvline(x0[0], ls='--', color='red', label='$x_0$')
ax[0].axhline(0, lw=0.5, ls='--', color='black')
ax[0].set_xticks([0, 1])
ax[0].set_xlabel('$x$')
ax[0].set_title('帰無仮説 $H_0:\\theta=0$\n$X \sim N(0,1)$')
ax[0].legend(loc='upper left')

# x0=1のときの1-α(x0)の確率
ax[1].plot(x, y_H0, color='steelblue', label='$H_0$')
ax[1].fill_between(x4, y4_H0, 0, color='green', alpha=0.3, label=r'$1-\alpha(x_0)$')
ax[1].axvline(x0[1], ls='--', color='red', label='$x_0$')
ax[1].axhline(0, lw=0.5, ls='--', color='black')
ax[1].set_xticks([0, 1])
ax[1].set_xlabel('$x$')
ax[1].set_title('帰無仮説 $H_0:\\theta=0$\n$X \sim N(0,1)$')
ax[1].legend(loc='upper left')

plt.show()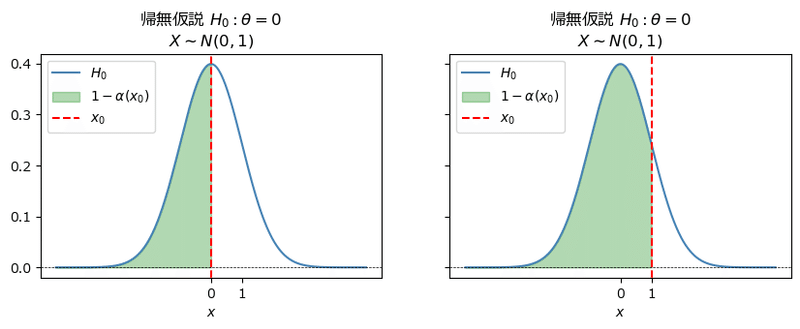

⑦$${\boldsymbol{\beta(x_0)}}$$の可視化
⑤のコードをコピーしてたたき台にしています。

### β(x0)の可視化

### プロット
fig, ax = plt.subplots(1,2, figsize=(10, 3), sharex=True, sharey=True)

## H1の分布、棄却域、β(x0)の値のプロット
# 棄却域塗りつぶし用
x5 = np.linspace(-5, x0[0], 101)
y5_H1 = H1.pdf(x5)
x6 = np.linspace(-5, x0[1], 101)
y6_H1 = H1.pdf(x6)

# x0=0のときの第２種の過誤β(x0)の確率
ax[0].plot(x, y_H1, color='orange', label='$H_1$')
ax[0].fill_between(x5, y5_H1, 0, color='orange', alpha=0.3, label=r'$\beta(x_0)$')
ax[0].axvline(x0[0], ls='--', color='red', label='$x_0$')
ax[0].axhline(0, lw=0.5, ls='--', color='black')
ax[0].set_xticks([0, 1])
ax[0].set_xlabel('$x$')
ax[0].set_title('対立仮説 $H_1:\\theta=1$\n$X \sim N(1,1)$')
ax[0].legend(loc='upper left')

# x0=1のときの第２種の過誤β(x0)の確率
ax[1].plot(x, y_H1, color='orange', label='$H_1$')
ax[1].fill_between(x6, y6_H1, 0, color='orange', alpha=0.3, label=r'$\beta(x_0)$')
ax[1].axvline(x0[1], ls='--', color='red', label='$x_0$')
ax[1].axhline(0, lw=0.5, ls='--', color='black')
ax[1].set_xticks([0, 1])
ax[1].set_xlabel('$x$')
ax[1].set_title('対立仮説 $H_1:\\theta=1$\n$X \sim N(1,1)$')
ax[1].legend(loc='upper left')

plt.show()

⑧計算した$${\boldsymbol{\beta(x_0), 1-\alpha(x_0)}}$$の値をプロット
前段で記事中に計算した$${\beta(x_0), 1-\alpha(x_0)}$$の値を設定して、後段でグラフの描画をしています。

### 計算したβ(x0)と1-α(x0)の値をプロット

# β(x0)と1-α(x0)の値を設定
B_x0 = [0.1587, 0.3085, 0.5]
one_a_x0 = [0.5, 0.6915, 0.843]

# プロット
plt.figure(figsize=(4, 4))
plt.plot(B_x0, one_a_x0, 'o-')
plt.xlabel(r'$\beta(x_0)$', fontsize=14)
plt.ylabel(r'$1-\alpha(x_0)$', fontsize=14)
plt.show()

⑧(β, 1-α)のグラフのプロット
前段で$${\alpha(x_0), \beta(x_0)}$$の値を計算して、後段でグラフの描画をしています。
$${\alpha(x_0)}$$は、H0の正規分布オブジェクトを用いて上側確率を算出しています。
$${\beta(x_0)}$$は、H1の正規分布オブジェクトを用いて下側確率（累積分布）を算出しています。

### (β, 1-α)のグラフのプロット

# x0が0~1のときのα(x0)、β(x0)を取得
x0 = np.linspace(0, 1, 101)
alpha_x0 = H0.sf(x0)
beta_x0 = H1.cdf(x0)

# (β(x0), 1-α(x0))のプロット
plt.figure(figsize=(4, 4))
plt.plot(beta_x0, 1-alpha_x0)
plt.plot((beta_x0[0], 1-alpha_x0[0]), (beta_x0[-1], 1-alpha_x0[-1]),
         '--', lw=0.8)
plt.xlabel(r'$\beta(x_0)$')
plt.ylabel(r'$1-\alpha(x_0)$')
plt.title(r'($\beta, 1-\alpha$)のグラフ')
plt.show()

Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。

おわりに

この問題では、文章を読んでもゴールへの道筋＝解法のイメージが湧きにくい、こんな体験をしました。
だったらグラフで可視化して考えよう！です。
正規分布の形状、$${\alpha,\beta}$$の領域、$${x_0}$$が動く様子などを感覚的に捉えると、標準正規分布の上側確率表にアプローチする道が見えてくるのではないでしょうか。

最後までお読みいただきまして、ありがとうございました。

のんびり統計シリーズの記事

次の記事

前の記事

目次