この記事は、テキスト「RとStanではじめる 心理学のための時系列分析入門」の第４章「RStanによる状態空間モデル」のRスクリプト・Stanコードをお借りして、PythonとPyMC Ver.5 で「実験的」に実装する様子を描いた統計ドキュメンタリーです。

取り扱いテーマは「観測値が離散量」である状態空間モデルです。
・観測値が二項分布に従うモデル
・観測値がポアソン分布に従うモデル

今回はPyMCでモデリングします。
まぁまぁ、諸々はさておいて、時系列分析とベイズモデリングを楽しんでいきましょう！

テキストの紹介、引用表記、シリーズまえがきは、このリンクの記事をご参照ください。

テキストで使用するデータは、R・Stan等のサンプルスクリプトで指定されています。
サンプルスクリプトは著者GitHubサイトからダウンロードして取得できます。

第４章 RStanによる状態空間モデル 

この記事は「4.3 観測値が離散量の場合」を実践いたします。

インポート（＋環境準備）

この記事で用いるライブラリをインポートします。

### インポート

# 基本
import numpy as np
import pandas as pd

# PyMC
import pymc as pm
import pytensor.tensor as pt
import arviz as az

# グラフ描画
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'

# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')

【補足】PyMC環境の構築
AnacondaでPyMC環境を構築する方法を次のリンクの「pymc環境の構築」の箇所に記載しています。
ご参考まで。

観測値が二項分布に従うモデル

観測値が０以上の整数＝カウントデータであり、上限が予め決まっている場合、二項分布を選択します。

二項分布に従うモデルで重要となる「標準ロジスティック関数」を描画しましょう。

### 標準ロジスティック関数
def logistic(x):
    return 1 / (1 + np.exp(-x))

x = np.linspace(-10, 10, 1001)
p = logistic(x)

fig, ax = plt.subplots(1, 1, figsize=(7, 3))
ax.plot(x, p)
ax.axvline(0, color='black', lw=0.5, ls='--')
ax.axhline(0.5, color='black', lw=0.5, ls='--')
ax.set(title='標準ロジスティック関数', xlabel=r'$\mu$', ylabel='p', xlim=(-5, 5));

【実行結果】
$${p}$$は0から1の間の値をとります。
標準ロジスティック関数を通すことで、$${\mu}$$の値を０～１の確率$${p}$$に収める、こんな感じです。
$${\mu=0}$$のとき$${p=0.5}$$になります。

テキストでは「授業の出席に関するデータ」を分析します。
ある学生が履修する授業に関して、先生が出席確認を行った回数を$${N_t}$$、その学生の実際の出席回数を目的変数$${Y_t}$$とし、その学生の出席意欲$${\mu_t}$$が関心のあるパラメータです。

モデルの数式です。

添字$${t}$$は時間（単位：日）です。
$${\theta_t}$$は出席確率であり、出席意欲$${\mu_t}$$を引数にするロジスティック関数で求めます。
目的変数である出席回数$${Y_t}$$は、試行回数＝出席確認回数$${N_t}$$、成功確率＝出席確率$${\theta_t}$$をパラメータにする二項分布に従います。

① データの作成・前処理
テキストのRコードに記載されたデータをお借りします。

### データの準備 # Rコードより引用

#日毎の出席回数
attend = (0,0,0,0,0,0,0,0,0,3,3,2,2,3,0,0,3,3,3,2,3,0,0,3,3,3,2,3,0,0,0,2,0,0,
          0,0,0,3,3,3,2,3,0,0,3,3,3,2,4,0,0,3,2,3,2,3,0,0,3,3,2,2,2,0,0,0,1,2,
          2,2,0,0,2,1,2,2,2,0,0,3,2,2,2,2,0,0,3,2,2,2,2,0,0,0,2,2,2,2,0,0,2,2,
          2,2,2,0,0,0,2,2,1,1,1,0,3,0,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
          0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
          1,1,1,2,3,0,0,1,1,2,2,3,0,0,1,1,2,2,3,0,0,1,1,0,0,0,0,0,1,1,2,2,3,0,
          0,0,1,1,2,3,0,0,1,1,1,0,0,0,0,0,2,2,1,3,0,0,1,2,2,2,3,0,0,1,1,2,2,3,
          0,0,1,1,2,2,3,0,0,1,1,1,1,3,0,0,1,1,2,2,3,0,0,0,1,0,2,3,0,0,0,0,0,0,
          0,0,0,0,0,0,0,0,0,0,0,0,2,2,3,0,0,1,2,2,2,3,0,0,1,0,0,0,0,0,0,0,0,0,
          0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
          0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0)

#日毎の出席確認回数
check = (0,0,0,0,0,0,0,0,0,3,3,3,2,3,0,0,4,4,4,2,3,0,0,4,4,4,2,3,0,0,4,4,0,0,0,
         0,0,4,4,4,2,3,0,0,4,4,4,2,4,0,0,4,4,4,2,3,0,0,4,4,3,2,3,0,0,3,3,2,2,2,
         0,0,3,3,2,2,2,0,0,3,3,2,2,2,0,0,3,3,2,2,2,0,0,3,3,2,2,2,0,0,2,3,2,2,2,
         0,0,0,3,2,1,1,1,0,3,0,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
         0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,2,2,2,3,
         0,0,1,2,2,2,3,0,0,1,2,2,2,3,0,0,1,1,2,2,3,0,0,1,2,2,2,3,0,0,1,2,2,2,3,
         0,0,1,2,2,0,0,0,0,0,2,2,2,3,0,0,1,2,2,2,3,0,0,1,2,2,2,3,0,0,1,2,2,2,3,
         0,0,1,2,2,2,3,0,0,1,2,2,2,3,0,0,1,1,0,2,3,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
         0,0,0,2,2,2,3,0,0,1,2,2,2,3,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
         0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
         0,0,0,0,0,0,0,0,0,0,0,0,0,0,0)

# データフレーム化
df_attend = pd.DataFrame({'Attend': attend, 'Check': check})
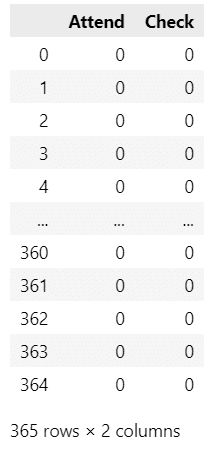
display(df_attend)

【実行結果】
365日分のデータです。
Attendは学生の出席回数、Checkは先生の出席確認回数です。

テキストにならって、データを描画します。
テキストの図4.15に相当します。

### 出席確認回数と出席数の描画　※図4.15に対応
plt.figure(figsize=(10, 4))
plt.plot(df_attend['Check'], label='出席確認')
plt.plot(df_attend['Attend'], color='tomato', lw=2, ls=':', label='出席')
plt.xlabel('日')
plt.ylabel('回数')
plt.legend(['出席', '出席確認'])
plt.show()

【実行結果】
回数＝０は夏休み等の長期休暇だそうです。

② モデルの定義
システムモデルの記述には「pm.GaussianRandomWalk()」を利用しました。
時系列分析感が出てきますね！

ロジスティック関数には、ロジット逆関数に相当する「pm.invlogit()」を利用しました。
尤度関数の二項分布は「pm.Binomial()」です。

### モデルの定義

with pm.Model() as model_bin:
    ### データ関連定義
    # coordの定義
    model_bin.add_coord('data', values=df_attend.index, mutable=True)
    # dataの定義
    y = pm.ConstantData('y', value=df_attend['Attend'].values, dims='data')
    x = pm.ConstantData('x', value=df_attend['Check'].values, dims='data')
    
    ### 事前分布
    sigma = pm.HalfCauchy('sigma', beta=5)
    # mu：システムモデル
    initDist = pm.Normal.dist(mu=0, sigma=sigma)
    mu = pm.GaussianRandomWalk('mu', mu=0, sigma=sigma, init_dist=initDist,
                               dims='data')
    # 出席確率：ロジットリンク関数の逆関数
    theta = pm.Deterministic('theta', pm.invlogit(mu), dims='data')

    ### 尤度：観測モデル
    likelihood = pm.Binomial('likelihood', n=x, p=theta, observed=y,
                             dims='data')

【実行結果】出力なし

③ モデルの表示・可視化
モデルの数式を表示します。

# モデルの表示
model_bin

【実行結果】

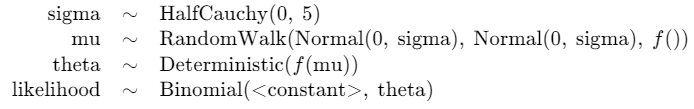
モデルを図にして可視化しましょう。

# モデルの可視化
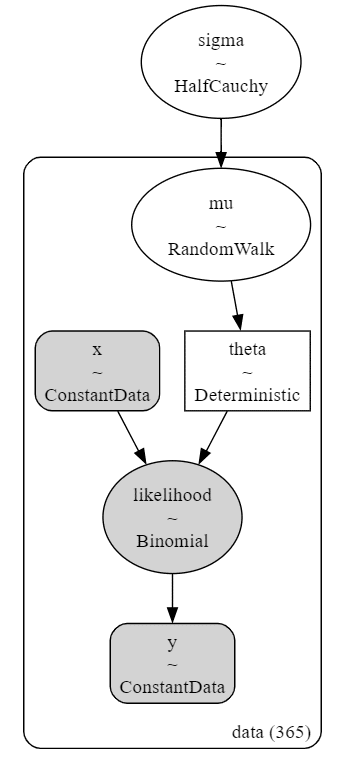
pm.model_to_graphviz(model_bin)

【実行結果】
シンプルなモデルです。

④ 事後分布からのサンプリング
MCMCを実行します。
NUTSサンプラーにnumpyroを利用します。
実行時間はおよそ3分30秒でした。

### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用　3分30秒
with model_bin:
    idata_bin = pm.sample(draws=2000, tune=5000, chains=4, target_accept=0.95,
                          nuts_sampler='numpyro', random_seed=1234)

【実行結果（一部）】

⑤ サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$としています。

### r_hat>1.1の確認
# 設定
idata_in = idata_bin     # idata名
threshold = 1.1          # しきい値

# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in).to_dataframe() > threshold).sum())

【実行結果】
$${\hat{R}>1.1}$$のパラメータは「0」件です。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

パラメータ等の事後分布の要約統計量です。

### 推論データの要約統計情報の表示
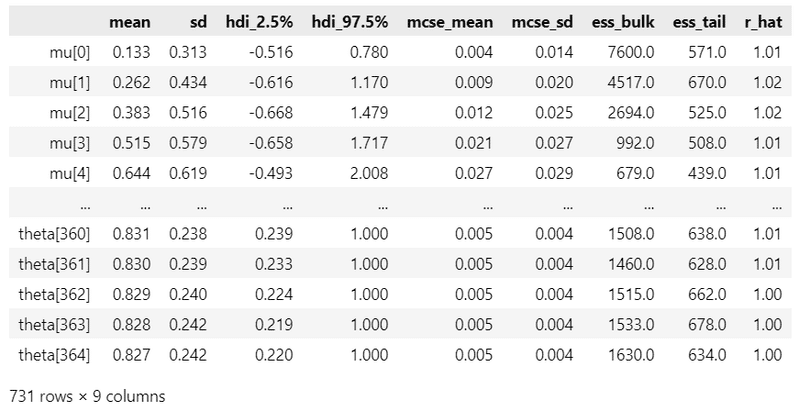
pm.summary(idata_bin, hdi_prob=0.95)

【実行結果】
パラメータ数が多いので省略表示となりました。

トレースプロットを確認しましょう。

### トレースプロットの表示
pm.plot_trace(idata_bin, combined=True, figsize=(10, 8))
plt.tight_layout();

【実行結果】
収束している感じがします。

⑥ 出席意欲と出席確率の描画
テキストの図4.16に相当する図を描画します。

### 出席意欲と出席確率の描画　※図4.16に相当

# 出席意欲の平均値、出席確率の中央値を算出
mu_mean = idata_bin.posterior.mu.stack(sample=('chain', 'draw')).mean(axis=1)
theta_median = (idata_bin.posterior.theta.stack(sample=('chain', 'draw'))
                .median(axis=1))

## 描画
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 5))

# 出席意欲
# 平均値の描画
ax1.plot(df_attend.index, mu_mean, label='mean')
# 95%HDIの描画
pm.plot_hdi(df_attend.index, idata_bin.posterior.mu, hdi_prob=0.95, ax=ax1,
            fill_kwargs={'color': 'tomato', 'alpha': 0.2, 'label': '95%HDI'})
# 505HDIの描画
pm.plot_hdi(df_attend.index, idata_bin.posterior.mu, hdi_prob=0.50, ax=ax1,
            fill_kwargs={'color': 'tomato', 'alpha': 0.5, 'label': '50%HDI'})
# 修飾
ax1.set(title=r'出席意欲$\mu$の事後期待値', xlabel='DAY', ylabel=r'\mu')
ax1.legend()
ax1.grid(lw=0.2)

# 出席確率
# 中央値の描画
ax2.plot(df_attend.index, theta_median, label='median')
# 95%HDIの描画
pm.plot_hdi(df_attend.index, idata_bin.posterior.theta, hdi_prob=0.95, ax=ax2,
            fill_kwargs={'color': 'tomato', 'alpha': 0.2, 'label': '95%HDI'})
# 50%HDIの描画
pm.plot_hdi(df_attend.index, idata_bin.posterior.theta, hdi_prob=0.50, ax=ax2,
            fill_kwargs={'color': 'tomato', 'alpha': 0.5, 'label': '50%HDI'})
# 修飾
ax2.set(title=r'出席確率$\theta$の事後中央値', xlabel='DAY', ylabel=r'$\theta$')
ax2.legend()
ax2.grid(lw=0.2)

plt.tight_layout()
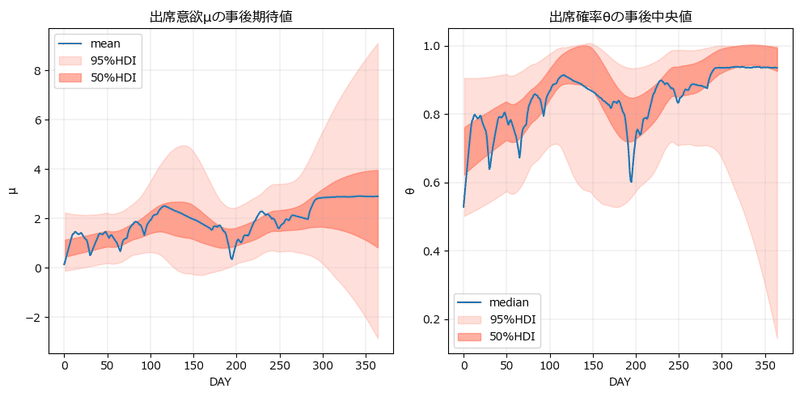
plt.show()

【実行結果】
左の出席意欲$${\mu}$$はテキストと見た目は近いです。
ただ、HDI区間（テキストは確信区間・信用区間）の幅はテキストよりも大きい感じがします。
右の出席確率$${\theta}$$はテキストよりも変動が大きく（特に200日あたり）、区間の幅も大きい結果になりました。

「y」の事後予測サンプリングを行って描画してみましょう。

### 事後予測のサンプリングの実施
with model_bin:
    idata_bin.extend(pm.sample_posterior_predictive(idata_bin,
                                                    random_seed=1234))

【実行結果】

描画します。

### 出席回数yの事後予測プロット

## 各種データの算出
# yの事後予測配列の取得 shape=(365, 8000)
y_pred = (idata_bin.posterior_predictive.likelihood
          .stack(sample=('chain', 'draw')).data)
# yの事後予測の平均値
y_mean = y_pred.mean(axis=1)
# yの事後予測の95%HDI区間
y_hdi95 = az.hdi(y_pred.T, hdi_prob=0.95)
# yの事後予測の50%HDI区間
y_hdi50 = az.hdi(y_pred.T, hdi_prob=0.50)

## 描画
plt.figure(figsize=(15, 5))
# 観測値の描画
plt.plot(df_attend.index, df_attend['Attend'], 'o', markersize=1, color='blue',
         label='観測値')
# yの事後予測の平均値の描画
plt.plot(df_attend.index, y_mean, color='tab:blue', lw=1, label='事後平均')
# yの事後予測の95%HDI区間の描画
plt.fill_between(df_attend.index, y_hdi95[:, 0], y_hdi95[:, 1], color='tomato',
                 alpha=0.2, label='95%HDI')
# yの事後予測の50%HDI区間の描画
plt.fill_between(df_attend.index, y_hdi50[:, 0], y_hdi50[:, 1], color='tomato',
                 alpha=0.5, label='50%HDI')
# 修飾
plt.xlabel('DAY')
plt.ylabel('出席回数')
plt.yticks([0, 1, 2, 3, 4])
plt.legend()
plt.show()

【実行結果】
50日ごろまで95%HDI区間は広めな感じです。4回出席まで伸びています。

観測値がポアソン分布に従うモデル

観測値が０以上の整数＝カウントデータであり、上限がない場合、ポアソン分布を選択します。

ポアソン分布は、一定期間のイベント平均発生回数$${\lambda}$$をパラメータにもつ離散型分布です。
ポアソン分布の確率質量関数の数式です。

この節で利用するデータは、60日間の毎日の行動生起回数$${\boldsymbol{Y_t}}$$をカウントしたデータであり、後半30日間に「介入」が入り、周期12の季節成分を含んでいます。

モデルの数式です。

① データの作成・前処理
テキストのRコードを参考にしてコード化しました。

【おことわり】
生成する乱数やフーリエ級数項の計算の相違などから、この記事で利用するデータはテキストと異なります。
したがいまして、推論結果もテキストと相違することを予めお断りいたします。

### データの準備 # Rコードより

# 初期値設定
np.random.seed(5)
N = 60            # 期間
mu_0 = 1          # muの状態初期値
sigma_S = 0.1     # muの標準偏差
mu_K = 1          # 介入効果の平均値
sigma_K = 0.1     # 介入効果の標準偏差

# 季節成分の生成
# 12か月周期のフーリエ級数の第２調和まで考慮、5年分作成
p = np.zeros(N)
t = np.arange(1, 13)
for i in range(1, 3):
    p = np.tile((np.random.random()*2-1) * np.cos(i*t) \
                 + (np.random.random()*2-1) * np.sin(i*t), N//len(t)+1)[:N] + p

# 介入系列の生成
IV = np.concatenate([np.zeros(30), np.ones(30)])
# 介入効果kの生成
k = np.random.normal(loc=mu_K, scale=sigma_K, size=N)
# 状態μの生成
mu = np.random.normal(loc=mu_0, scale=sigma_S)
# 観測値の生成
observation = np.random.poisson(lam=np.exp(mu + k * IV + p), size=N)

# データフレーム化
df_poi = pd.DataFrame({'obs': observation, 'IV': IV, 'mu': mu, 'k': k,
                       'season': p})
print('df_poi.shape:', df_poi.shape)
display(df_poi.head())

【実行結果】
60日分のデータです。
以下は項目内容です。
・obs：日々の行動生起回数$${Y_t}$$
・IV：介入フラグ（0：介入なし、1：介入あり、30日目以降に1を設定）
・mu：データ生成時に計算した状態$${\mu}$$
・season：データ生成時に計算した季節成分

テキストにならって、データを描画します。
テキストの図4.17に相当します。

### 描画 ★図4.17に相当
plt.figure(figsize=(12, 4))
plt.plot(df_poi.index, df_poi['obs'])
plt.hlines(-1, 30, 60, lw=8, alpha=0.5)
plt.xlabel('Time')
plt.ylabel('observation');

【実行結果】
介入が入った30日以降で変動が大きくなっています。

② モデルの定義
レベル成分の記述には「pm.GaussianRandomWalk()」を、季節成分の記述には「pm.AR()」をそれぞれ利用しました。
PyMC時系列分析オールスターズです！

対数リンク関数の逆関数＝自然対数の底$${e}$$のべき乗関数には、pytensorの関数「pt.exp()」を利用しました。
関数内で線形予測子の計算をしています。
尤度関数のポアソン分布は「pm.Poisson()」です。

### モデルの定義

# 季節成分を実装するARパラメータの設定
period = 12                    # 季節成分の周期
order = period - 1             # ARの次数
rhos = np.ones(order) * -1     # ARのρパラメータ

with pm.Model() as model_poi:
    ### データ関連定義
    # coordの定義
    model_poi.add_coord('data', values=df_poi.index, mutable=True)
    # dataの定義
    y = pm.ConstantData('y', value=df_poi['obs'].values, dims='data')
    IV = pm.ConstantData('IV', value=df_poi['IV'].values, dims='data')
    
    ### 事前分布
    sigmaS = pm.Uniform('sigmaS', lower=0, upper=100)
    sigmaSeason = pm.Uniform('sigmaSeason', lower=0, upper=100)
    k = pm.Uniform('k', lower=-100, upper=100)
    # mu：レベル成分
    init_dist_mu = pm.Normal.dist(mu=0, sigma=sigmaS)
    mu = pm.GaussianRandomWalk('mu', mu=0, sigma=sigmaS, init_dist=init_dist_mu,
                               dims='data')
    # season：季節成分
    init_dist_season = pm.Normal.dist(mu=0, sigma=sigmaSeason)
    season = pm.AR('season', rho=rhos, sigma=sigmaSeason, constant=False,
                   init_dist=init_dist_season, ar_order=order, dims='data')
    # 対数リンク関数の逆関数
    lam = pm.Deterministic('lam', pt.exp(mu + k * IV + season), dims='data')

    ### 尤度：観測モデル
    likelihood = pm.Poisson('likelihood', mu=lam, observed=y, dims='data')

【実行結果】出力なし

③ モデルの表示・可視化
モデルの数式を表示します。

### モデルの表示
model_poi

【実行結果】

モデルを図にして可視化しましょう。

# モデルの可視化
pm.model_to_graphviz(model_poi)

【実行結果】
シンプルなモデルです。

④ 事後分布からのサンプリング
MCMCを実行します。
NUTSサンプラーにnumpyroを利用します。
実行時間はおよそ30秒でした。

### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用　30秒
with model_poi:
    idata_poi= pm.sample(draws=6000, tune=2000, chains=4, target_accept=0.9,
                         nuts_sampler='numpyro', random_seed=1234)

【実行結果（一部）】

⑤ サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$としています。

### r_hat>1.1の確認
# 設定
idata_in = idata_poi     # idata名
threshold = 1.1          # しきい値

# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in).to_dataframe() > threshold).sum())

【実行結果】
$${\hat{R}>1.1}$$のパラメータは「0」件です。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

パラメータ等の事後分布の要約統計量です。
日別ではないパラメータに限定して出力します。

### 推論データの要約統計情報の表示
var_names = ['k', 'sigmaS', 'sigmaSeason']
pm.summary(idata_poi, hdi_prob=0.95, var_names=var_names)

【実行結果】
介入の効果の平均値は$${1.366}$$です。
データ生成時の各パラメータの値とはあまり近くない結果になりました（汗）

（参考：データ生成時のパラメータ値）

トレースプロットを確認しましょう。
こちらは全パラメータを表示しましょう。

### トレースプロットの表示
pm.plot_trace(idata_poi, combined=True, figsize=(10, 10))
plt.tight_layout();

【実行結果】
収束している感じがします。

⑥ 介入効果$${\boldsymbol{k}}$$の描画
テキストの図4.18に相当する図を描画します。

### 介入効果kの事後分布　※図4.18に相当
pm.plot_posterior(idata_poi, var_names='k', hdi_prob=0.95, figsize=(5, 3));

【実行結果】
95%HDIは$${[0.11,\ 2.6]}$$であり正の値です。
介入には正の効果があると考えられます。

テキストのように介入効果$${k}$$の事後分布の中央値、95%確信区間を求めてみます。

# 介入効果kの事後中央値、95%CIの計算
tmp = idata_poi.posterior.k
k_median = tmp.median().data
k_ci0025 = tmp.quantile(q=0.025).data
k_ci0975 = tmp.quantile(q=0.975).data
print(f'k: {k_median:.3f} (95%CI= ({k_ci0025:.3f}, {k_ci0975:.3f}])')

【実行結果】

⑦ 事後分布サンプリングデータにて目的変数「y」を予測
テキストの図4.19に相当する目的変数「y」の予測値を計算して、描画しましょう。
事後分布サンプリングデータの$${\mu, k}$$と介入実績$${IV}$$を用いて、「y」を予測します。
季節成分が除外されていることに留意しましょう。

### 季節調整済行動生起回数の事後分布の描画　※図4.19に相当

## データの準備
# サンプルデータでμ＋IVｘkを計算 shape=(60, 24000)
y_pred_tmp = (np.exp(idata_poi.posterior.mu.stack(sample=('chain', 'draw')).data 
              + df_poi['IV'].values.reshape(-1, 1) 
              * idata_poi.posterior.k.stack(sample=('chain', 'draw')).data))
# y_predの平均値の計算 shape=(60)
y_pred_mean = y_pred_tmp.mean(axis=1)
# y_predのHDIの計算 shape=(60, 2)
y_pred_hdi = az.hdi(y_pred_tmp.T)

## 描画
plt.figure(figsize=(12, 4))
plt.plot(df_poi.index, y_pred_mean)
plt.fill_between(df_poi.index, y_pred_hdi[:, 0], y_pred_hdi[:, 1], alpha=0.2)
plt.xlabel('Time')
plt.ylabel(r'Pred: $\mu \times IV$');

【実行結果】
30日以降、生起回数は増えている様子が分かります。
薄い青色の95%HDIは30日以降の方が幅が広くなっています。

以上で終了です。
お疲れ様でした。

まとめ

• 観測値が離散量のケースをモデリングして、二項分布・ポアソン分布といった離散型分布を利用しました。

• モデリングの精度はテキストよりも劣る結果になりました（汗）

（参考）推論データ（idata）の保存コード
pickle形式で保存します。

### idataの保存 pickle
# ユーティリティ
import pickle

file = r'ch04_04_idata_bin.pkl'
with open(file, 'wb') as f:
    pickle.dump(idata_bin, f)

file = r'ch04_04_idata_poi.pkl'
with open(file, 'wb') as f:
    pickle.dump(idata_poi, f)

読み込みコードは次のとおりです。
「file」のパス＆ファイル名と「idata_bin_load」を適宜変更してお使い下さい。

### idataの読み込み（例）
file = r'ch04_04_idata_bin.pkl'
with open(file, 'rb') as f:
    idata_bin_load = pickle.load(f)

第４章 その５ へ続く

■次回の取り組みテーマ
引き続き、状態空間モデルを学びます。
推測するパラメータが離散値のケースです。
・変化点モデル
・隠れマルコフモデル

次の記事

前の記事

目次

ブログの紹介

note で４つのシリーズ記事を書いています。
ぜひ覗いていってくださいね！

１．のんびり統計
統計検定２級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定２級公式問題集CBT対応版に対応しています。

２．実験！たのしいベイズモデリングをPyMC Ver.5で

書籍「たのしいベイズモデリング」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは Ｒ言語＋Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう！

３．Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learn と PyTorch の教科書です。
よかったらぜひ、お試しくださいませ。

４．データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Python のコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。

最後までお読みいただきまして、ありがとうございました。