この記事は、テキスト「たのしいベイズモデリング」の第４章「ことばの背後にある意図を探る傾向の個人差」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。

今回は初学者に優しい入門編的なモデルです。
しかも！初の「ほぼ再現」を実現できました！

果たして間接的発話から要求を汲み取る力の個人差にはどのような傾向があるのでしょうか？
PyMCでモデリングして、ベイズ推論を楽しみましょう！

テキストの紹介、引用表記、シリーズまえがき、PyMC等のバージョン情報は、このリンクの記事をご参照ください。

テキストで使用するデータは、R・Stan等のサンプルスクリプトとともに、出版社サイトからダウンロードして取得できます。

サマリー

テキストの概要

執筆者　　　：　平川真 先生
モデル難易度：　★・・・・　（やさしい）

自己評価

評点

$$
\begin{array}{c:c:c}
実装精度 & ★★★★★& GoooD!\\
結果再現度 & ★★★★★& 最高✨\\
楽しさ & ★★★★★ & 楽しい！ \\
\end{array}
$$

評価ポイント

• はじめて事後分布の要約統計量がおおむね一致しました！やったね！

• ２項分布と混合２項分布のベイズモデルは、PyMCの学びに丁度よい難易度です。テキストには親切で丁寧なモデルの説明が掲載されています。

工夫・喜び・反省

「たのしいベイズモデリング」の実践で初めてガッツポーズが出ました💪
テキストの結果を再現できて、そして、PyMCによるベイズ推論を噛み締めることができて、とても嬉しいです😆

モデルの概要

テキストの調査・実験の概要

図の発話例のように、直接的に要求の言葉を発していないけれども、状況等から何かの要求があると解釈するのは、日常的によくあるシーンです。

人によっては「要求されたと思う」「要求など無いと思う」というように、解釈の相違や、要求と受け止めやすい／受け止めにくいという傾向の違いがあるようです。

テキストの執筆者は、このような間接的な発話に対して要求があるのか無いのかの「判断の個人差の傾向」を探るために、ベイズモデリングを導入したのです！

テキストのモデリング

■目的変数と関心のあるパラメータ
目的変数$${y_{i}}$$は「要求と解釈した数」です。
試行回数$${n=7}$$（設問数）、成功確率$${\theta}$$の２項分布に従うとしています。
テキストでは成功確率$${\theta}$$を「要求の解釈率」と呼んでいます。
関心のあるパラメータはこの「要求の解釈率」$${\theta}$$です。
添字$${i}$$は回答者400人のIDです（$${i=1, \cdots, 400}$$）。

■要求の解釈率に切り込む２つのモデル
テキストは２つの「要求の解釈率」を仮定して２つのモデルで分析しています。

1. 個人ごとに異なる解釈率$${\theta_i}$$を仮定した２項分布モデル

2. グループごとに異なる解釈率$${\theta_1,\ \theta_2}$$を仮定した混合２項分布モデル

■個人ごとに異なる解釈率$${\theta_i}$$を仮定した２項分布モデル
$${r_i}$$は解釈率の個人差を示し、正規分布に従うと仮定しています。

■グループごとに異なる解釈率$${\theta_1,\ \theta_2}$$を仮定した混合２項分布モデル
要求かどうかの解釈の傾向が２つにグルーピングされると仮定するモデルです。
２つのグループの解釈率の大小関係は$${\theta_1 < \theta_2}$$です。

混合２項分布$${\text{Binomial\_Mixture}}$$の詳細は次式のとおりです。
$${\pi}$$はデータが１つ目の２項分布から発生する確率です。

■分析・分析結果
分析結果はテキストに記載のとおりです。
PyMCモデリングでの分析結果は、「PyMC実装」章の【分析】の部分をご覧ください。

PyMC実装

Let's enjoy PyMC & Python !

準備・データ確認

１．インポート

### インポート

# ユーティリティ
import pickle

# 数値・確率計算
import pandas as pd
import numpy as np

# PyMC
import pymc as pm
import pytensor.tensor as pt
import arviz as az

# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'

# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')

２．データの読み込み
csvファイルをpandasのデータフレームに読み込みます。

# データの読み込み
data = pd.read_csv('data_hirakawa.csv')
display(data)

【実行結果】
回答者個人は変数「no」で識別されています。
変数「y」を目的変数に用います。
「y」は７つの設問「p1～p7」の回答値の合計です。
p1～p7には、予め定められた７つの間接的発話を要求として解釈するのが正しいと判断する場合に１、間違っていると判断する場合に０がそれぞれ設定されています。

３．データの外観・統計量

要約統計量を確認します。

### 要約統計量の表示
data.describe().round(2)

【実行結果】

p1～p7とyのヒストグラムを確認しましょう。

### p1～yのヒストグラムの描画
plt.figure(figsize=(12, 6))
for i, col in enumerate(data.columns[3:]):
    plt.subplot(2, 4, i+1)
    plt.hist(data[col], bins=8, edgecolor='white')
    plt.title(col)
plt.tight_layout()

【実行結果】
p1～p7の回答の傾向にはバラツキが見られます。
要求であると判断する傾向が高いのはp3、p5、p6、要求ではないと判断する傾向が高いのはp1、p4のようです。
p2とp7は意見の分かれる設問のようです。

モデル１の実装

「解釈率が個人ごとに異なると仮定した２項分布」のモデリングです。

モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
パラメータ$${\mu,\ \sigma}$$の一様分布の範囲には$${100}$$を用いました。

$$
\begin{align*}
\mu &\sim \text{Uniform}(-100, 100) \\
\sigma &\sim \text{Uniform}(0, 100) \\
r_i &\sim \text{Normal}(\text{mu}=\mu,\ \text{sigma}=\sigma) \\
\theta_i &= \text{logistic}(r_i) \\
likelihood &\sim \text{Binomial}(\text{n}=7,\ \text{p}=\theta_i) \\
\end{align*}
$$

１．モデルの定義
初期値、coord、data、パラメータの事前分布、尤度をそれぞれ指定します。

### モデルの定義

# 初期値設定
n = 7            # 発話数 7

# モデルの定義
with pm.Model() as model1:
    
    ### データ関連定義
    # coordの定義
    model1.add_coord('data', data.index, mutable=True)
    # dataの定義
    y = pm.ConstantData('y', value=data['y'], dims='data')
    
    ### 事前分布
    # 事前分布
    mu = pm.Uniform('mu', lower=-100, upper=100)
    sigma = pm.Uniform('sigma', lower=0, upper=100)
    r = pm.Normal('r', mu=mu, sigma=sigma, dims='data')
    # θ ロジスティック関数:invlogit
    theta = pm.Deterministic('theta', pm.invlogit(r), dims='data')

    ### 尤度
    likelihood = pm.Binomial('likelihood', n=n, p=theta, observed=y,
                             dims='data')

【モデル注釈】

• coordの定義
  座標に名前を付けたり、その座標が取りうる値を設定できます。
  今回は次の１つを設定しました
  ・行の座標：名前「data」、値「行インデックス」
  　回答者個人の識別子$${i=0, \cdots, 399}$$を兼ねています。

• dataの定義
  目的変数$${y}$$を設定しました。

• パラメータの事前分布
  モデルの数式表現のとおりにmu、sigma、rを設定しました。
  r の次元は「data」（≒回答者個人）です。

• ロジスティック関数
  thetaの算出に用いるロジスティック関数には「pm.invlogit()」を利用しました。

• 尤度
  次元は「data」です。

２．モデルの外観の確認

### モデルの表示
model1

【実行結果】

# モデルの可視化
pm.model_to_graphviz(model1)

【実行結果】
縦長の構造です（上部には隠れミ◯キーが！？）

３．事後分布からのサンプリング
乱数生成数（draws, tune, chains）はテキストどおりです。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ50秒でした。

### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用　50秒
with model1:
    idata1 = pm.sample(draws=25000, tune=5000, chains=4, target_accept=0.9,
                       nuts_sampler='numpyro', random_seed=1234)

【実行結果】省略

４．サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$としています。

### r_hat>1.1の確認
rhat_idata1 = az.rhat(idata1)
(rhat_idata1 > 1.1).sum()

【実行結果】
$${\hat{R} > 1.1}$$のパラメータは「0」件です。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

パラメータ$${\mu,\ \sigma}$$の事後分布の要約統計量です。

### 推論データの要約統計情報の表示
var_names = ['mu', 'sigma']
pm.summary(idata1, hdi_prob=0.95, var_names=var_names)

【実行結果】
EAP（mean）、post.sd（sd）、2.5%（hdi_2.5%）、97.5%（hdi_97.5%）の値はテキストとほぼ同じです！（やったー！）
なお、テキストの95%区間は信用区間ですが、summary関数の95%区間はHDI区間です。

トレースプロットです。

### トレースプロットの描画
pm.plot_trace(idata1, var_names=var_names, combined=True, figsize=(12, 7))
plt.tight_layout();

【実行結果】
きれいなトレースプロットです。収束している感触を満喫しました。

５．分析～テキストにならって

①パラメータ$${\mu,\ \sigma}$$の事後分布の確認
テキストの図4.1を代替するヒストグラムを描画します。

### muとsigmaの事後分布ヒストグラムの描画 ★図4.1に対応

# 事後分布サンプリングデータからmuとsigmaを取り出し
mu_data = idata1.posterior.mu.data.flatten()
sigma_data = idata1.posterior.sigma.data.flatten()

# 描画用リストの作成
plot_list = [mu_data, sigma_data]          # サンプリングデータ
title_list = [r'$\mu$', r'$\sigma$']       # グラフタイトル

# 2つのヒストグラムの描画
plt.figure(figsize=(10, 4))
for i, (p, t) in enumerate(zip(plot_list, title_list)):  
    ax = plt.subplot(1, 2, i+1)
    sns.histplot(p, bins=30, kde=True, stat='density', element='step', ax=ax)
    ax.set_title(t, fontsize=14)
# 修飾
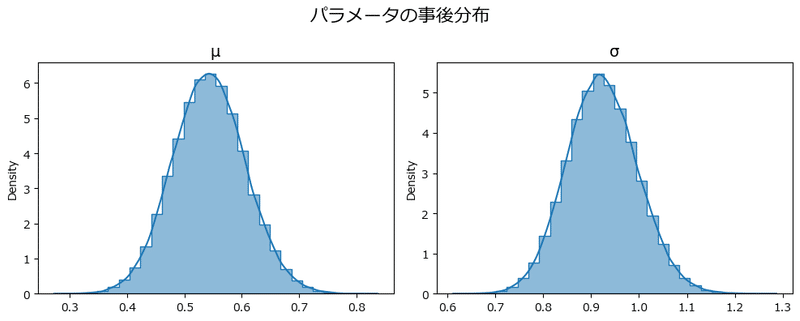
plt.suptitle('パラメータの事後分布', fontsize=16)
plt.tight_layout()
plt.show()

【実行結果】
きれいなベル型です。

続いて要約推定量を表示します。テキストの表4.2を代替します。

### パラメータの事後分布の要約統計量　★表4.2に対応（ただしMAPは省略）

# 要約統計情報を計算する関数の定義
def calc_stat(x):
    return [np.mean(x), np.std(x), np.quantile(x, 0.025), np.median(x),
            np.quantile(x, 0.975)]

pd.DataFrame({'μ': calc_stat(mu_data),
              'σ': calc_stat(sigma_data)},
             index=['EAP', 'post.sd', '0.025', 'MED', '0.975']
             ).T.round(3)

【実行結果】
テキストの統計値とおおむね一致しています。

テキストにならって、$${\mu}$$の$${95\%}$$信用区間$${[0.42, 0.67]}$$をロジスティック関数を通して変換して、確率値を確認しましょう。

### 平均muのlogistic変換後の信用区間　★4.4.2 分析結果と結果の解釈に対応

# ロジスティック関数の関数定義
def logistic(x):
    return 1 / (1 + np.exp(-x))

mu025, mu975 = 0.42, 0.67

print(f'logistic変換後の平均の95%信用区間: '
      f'{logistic(mu025):.2f} - {logistic(mu975):.2f}')

【実行結果】
要求の解釈率の平均の$${95\%}$$信用区間は$${[0.60, 0.66]}$$です。
全体的に６割強が「要求である」とする解釈率のようです。

②$${\theta_i}$$の事後分布のヒストグラムの描画
テキストの図4.2を代替するものです。
テキストでは事後予測サンプリングを実行して$${\theta_i}$$を生成しているようですが、ここでは事後分布サンプリング時に取得した$${\theta_i}$$を利用します。

### thetaの事後分布ヒストグラムの描画 ★図4.2に対応
# alpha,betaの事後分布サンプルに基づくrの事後予測を実施していません

# 事後分布サンプリングデータからthetaを取り出し
theta_data = idata1.posterior.theta.data.flatten()

# thetaの2.5%点、97.5%点の取得
q0025 = np.quantile(theta_data, 0.025)
q0975 = np.quantile(theta_data, 0.975)
q0100 = np.quantile(theta_data, 0.1)
q0900 = np.quantile(theta_data, 0.9)

# thetaのヒストグラムの描画
plt.figure(figsize=(8, 3))
plt.hist(theta_data, bins=101, density=True, alpha=0.5)
# 95%信用区間の境界線の描画
plt.axvline(q0025, color='black', lw=1, ls='--', label='95%区間')
plt.axvline(q0975, color='black', lw=1, ls='--')
# 80%信用区間の境界線の描画
plt.axvline(q0100, color='red', lw=1, ls='--', label='80%区間')
plt.axvline(q0900, color='red', lw=1, ls='--')
# 修飾
plt.xticks([0, 0.25, 0.5, 0.75, 1])
plt.yticks([0, 0.5, 1, 1.5, 2])
plt.title(rf'$\theta_i$ の事後分布, 95%信用区間:{q0025:.2f}-{q0975:.2f}',
          fontsize=14)
plt.ylabel('確率密度')
plt.legend(fontsize=12)
plt.show()

【実行結果】

【分析】
テキストの分析の仕方を利用させていただき、書きます。
要求の解釈率$${\theta_i}$$の$${95\%}$$信用区間は$${[0.23,\ 0.92]}$$であり、かなり幅があるようです。
これは間接的発話が要求かどうかの解釈率には個人差が大きいことを示唆しているようです。
ヒストグラムは右側（上側）に偏り気味であり、「要求である」と解釈する傾向の方が高い感じです。

６．推論データ（idata）の保存
推論データを再利用する場合に備えてファイルに保存しましょう。
idata1をpickleで保存します。

### idataの保存 pickle
file = r'idata1_ch04.pkl'
with open(file, 'wb') as f:
    pickle.dump(idata1, f)

読み込みコードは次のとおりです。

### idataの読み込み pickle
file = r'idata1_ch04.pkl'
with open(file, 'rb') as f:
    idata1_load = pickle.load(f)

モデル２の実装

「解釈率が異なるグループの存在を仮定した混合２項分布」のモデリングです。

モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
パラメータ$${\theta_1,\ \theta_2}$$の一様分布の範囲には$${10}$$を用いました。
※$${100}$$を用いる場合、事後分布の要約統計量がテキストと異なる結果になりました。

$$
\begin{align*}
\pi &\sim \text{Uniform}(0, 1) \\
w &= [\pi,\ 1-\pi] \\
\theta_{tmp1},\theta_{tmp2} &\sim \text{Uniform}(-10, 10) \\
\theta_1 &= \text{logistic}(\theta_{tmp1}) \\
\theta_2 &= \text{logistic}(\theta_{tmp2}) \\
components &= [ \\
&\text{Binomial.dist}\ (\text{n}=7,\ \text{p}=\theta_1), \\
&\text{Binomial.dist}\ (\text{n}=7,\ \text{p}=\theta_2) \\
&]\\
likelihood &\sim \text{Mixture}\ (\text{comp\_dist}=components,\ \text{weight}=w)\\
\end{align*}
$$

１．モデルの定義
初期値、coord、data、パラメータの事前分布、尤度をそれぞれ指定します。

### モデルの定義

# 初期値設定
n = 7            # 発話数 7

# モデルの定義
with pm.Model() as model2:
    
    ### データ関連定義
    # coordの定義
    model2.add_coord('data', data.index, mutable=True)
    # dataの定義
    y = pm.ConstantData('y', value=data['y'], dims='data')
    
    ### 事前分布
    # 分布の混合割合pi：[pi, 1-pi]を二項分布の構成比率wに格納
    pi = pm.Uniform('pi', lower=0, upper=1)
    w = pt.stack([pi, 1-pi])
    
    # 二項分布のパラメータθ1,θ2：logistic変換前の一時変数thetaTmp
    thetaTmp = pm.Uniform('thetaTmp', lower=-10, upper=10, shape=2)
    # thetaTmp1 <= thetaTmp2となるように設定
    thetaTmp1 = pm.Deterministic('thetaTmp1',
                                 pt.switch(thetaTmp[0] < thetaTmp[1],
                                           thetaTmp[0], thetaTmp[1]))
    thetaTmp2 = pm.Deterministic('thetaTmp2',
                                 pt.switch(thetaTmp[0] < thetaTmp[1],
                                           thetaTmp[1], thetaTmp[0]))
    
    # 二項分布のパラメータθ1,θ2：logistic変換
    theta1 = pm.Deterministic('theta1', pm.invlogit(thetaTmp1)) 
    theta2 = pm.Deterministic('theta2', pm.invlogit(thetaTmp2)) 
    
    ### 尤度
    # 混合する二項分布の構成
    components = [
        pm.Binomial.dist(n=n, p=theta1),  # p=theta値の小さいグループ
        pm.Binomial.dist(n=n, p=theta2),  # p=theta値の大きいグループ
    ] 
    # 尤度
    likelihood = pm.Mixture('likelihood', w=w, comp_dists=components,
                            observed=y, dims='data')

【モデル注釈】
モデル１との違いを中心に説明します。

• パラメータの事前分布
  モデルの数式表現のとおりにpi、thetaTmp（要素２つ）を設定しました。
  thetaTmp1 ＜ thetaTmp2 となるように、pt.switch() の箇所で thetaTmp の２つの要素のうち小さな値をthetaTmp1に 大きな値をthetaTmp2に設定しています。

• ロジスティック関数
  theta1, theta2の算出に用いるロジスティック関数には「pm.invlogit()」を利用しました。

• 混合分布は次のように実装しました。

  • 尤度likelihoodで混合分布「pm.Mixture」を指定。混合分布の構成は「components」を参照。各分布の重み（混合割合）はwで指定。

  • componentsのリストでは、成功確率パラメータpにtheta1とtheta2を指定する２つの２項分布を指定。

２．モデルの外観の確認

### モデルの表示
model2

【実行結果】

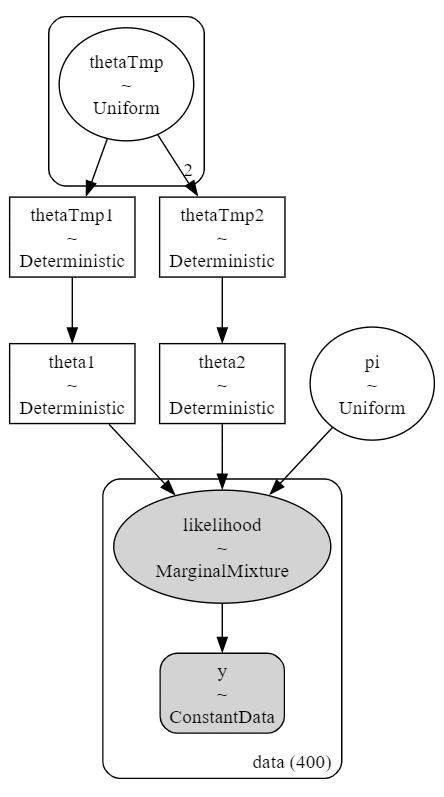
### モデルの可視化
pm.model_to_graphviz(model2)

【実行結果】
縦長の構造です。

３．事後分布からのサンプリング
乱数生成数（draws, tune, chains）はテキストどおりです。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ30秒でした。

### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用　30秒
with model2:
    idata2 = pm.sample(draws=25000, tune=5000, chains=4, target_accept=0.9,
                       nuts_sampler='numpyro', random_seed=1234)

【実行結果】省略

４．サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$としています。

### r_hat>1.1の確認
rhat_idata1 = az.rhat(idata1)
(rhat_idata1 > 1.1).sum()

【実行結果】
thetaTmpが$${\hat{R} > 1.1}$$です・・・

事後分布の要約統計量を確認しましょう。

### 推論データの要約統計情報の表示
pm.summary(idata2, hdi_prob=0.95)

【実行結果】
thetaTmp[0]と[1]は、値の小さな方をthetaTmp1へ、大きな方をthetaTmp2に割り当てています。

トレースプロットの確認をしましょう。

### トレースプロットの描画
pm.plot_trace(idata2, combined=True, figsize=(12, 10))
plt.tight_layout();

【実行結果】
thetaTmp以外は収束している感じです。
thetaTmpは０付近と2.4付近に２つの峰があります。
この値はthetaTmp1とthetaTmp2の値に近似しています。
thetaTmp・thetaTmp1・thetaTmp2の三位一体で収束している、という風に解釈して、分析に進みましょう（汗）

５．分析～テキストにならって

①パラメータ$${\pi,\ \theta_1,\ \theta_2}$$の事後分布の確認
テキストの図4.3を代替するヒストグラムを描画します。

### pi, theta1, theta2の事後分布のヒストグラムの描画 ★図4.3に対応

# 事後分布サンプリングデータからpi,theta1,theta2を取り出し
pi_data = idata2.posterior.pi.data.flatten()
theta1_data = idata2.posterior.theta1.data.flatten()
theta2_data = idata2.posterior.theta2.data.flatten()

# 描画用リストの作成
plot_list = [pi_data, theta1_data, theta2_data]          # サンプリングデータ
title_list = [r'$\pi$', r'$\theta_1$', r'$\theta_2$']    # グラフタイトル

# 3つのヒストグラムの描画
plt.figure(figsize=(10, 4))
for i, (p, t) in enumerate(zip(plot_list, title_list)):  
    ax = plt.subplot(1, 3, i+1)
    sns.histplot(p, bins=30, kde=True, stat='density', element='step', ax=ax)
    ax.set_title(t, fontsize=14)
# 修飾
plt.suptitle('パラメータの事後分布', fontsize=16)
plt.tight_layout()
plt.show()

【実行結果】
きれいなベル型です。

続いて要約推定量を表示します。テキストの表4.3を代替します。

### パラメータの事後分布の要約統計量　★表4.3に対応（ただしMAPは省略）

# 要約統計情報を計算する関数の定義
def calc_stat(x):
    return [np.mean(x), np.std(x), np.quantile(x, 0.025), np.median(x),
            np.quantile(x, 0.975)]

pd.DataFrame({'π': calc_stat(pi_data),
              'θ1': calc_stat(theta1_data),
              'θ2': calc_stat(theta2_data)},
             index=['EAP', 'post.sd', '0.025', 'MED', '0.975']
             ).T.round(3)

【実行結果】
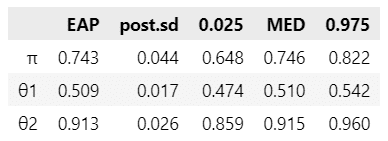
テキストの統計値とおおむね一致しています。

【分析】
テキストの分析の仕方を利用させていただき、書きます。

• ２つのグループの解釈率の平均は、およそ0.51と、およそ0.91です。

• 0.51のグループは$${\theta_1}$$の$${95\%}$$信用区間が$${0.47～0.54}$$であり、設問に対して半々の解釈率を傾向とするグループのようです。

• 0.91のグループは$${\theta_2}$$の$${95\%}$$信用区間が$${0.86～0.96}$$であり、「要求である」と判断する傾向が高いグループです。

• 混合分布の１つ目（$${\theta_1}$$を含む方）の重み$${\pi}$$は、平均値がおよそ0.74、$${95\%}$$信用区間が$${0.65～0.82}$$です。
  $${95\%}$$信用区間の範囲外である$${\boldsymbol{0.18～0.35}}$$が「非常に間接的発話を要求と解釈しやすい人」である確率とのことです。

６．推論データ（idata）の保存
推論データを再利用する場合に備えてファイルに保存しましょう。
idata2をpickleで保存します。

### idataの保存 pickle
file = r'idata2_ch04.pkl'
with open(file, 'wb') as f:
    pickle.dump(idata2, f)

読み込みコードは次のとおりです。

### idataの読み込み pickle
file = r'idata2_ch04.pkl'
with open(file, 'rb') as f:
    idata2_load = pickle.load(f)

以上で第４章は終了です。

おわりに

間接的な要求の汲み取りやすさ

テキストの執筆者は大学時代の経験で「自分が間接的な発話の理解が苦手である」と認識されたそうです。
私も自分のことを同じように認識しています。
言葉の解釈は難しいのです。。。

今回の執筆者の調査により、$${18～35\%}$$程度の人が間接的発話が要求であると非常に判断しやすい人と推定されました。
逆に、要求であるとほどんど判断しない人はどの程度の確率で存在するのでしょう。
３つの混合２項分布モデルで・・・、いや、何でも無いです。

PyMCでテキストの混合２項分布モデルによる分析にたどり着けたことは、とても喜ばしいことです。
そして、続きが気になります。
（$${18～35\%}$$程度の人が３つの混合２項分布モデルの実践を要求していると感じとってくれているはず）

シリーズの記事

次の記事

前の記事

目次

ブログの紹介

note で４つのシリーズ記事を書いています。
ぜひ覗いていってくださいね！

１．のんびり統計
統計検定２級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定２級公式問題集CBT対応版に対応しています。

２．RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析トピックを PythonとPyMC Ver.5で取り組みます。
豊富なテーマ（お題）を実践することによって、PythonとPyMCの基礎体力づくりにつながる、そう信じています。
日々、Web検索に勤しみ、時系列モデルの理解、Pythonパッケージの把握、R・Stanコードの翻訳に励んでいます！
このシリーズがPython時系列分析の入門者の参考になれば幸いです🍀

３．Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learn と PyTorch の教科書です。
よかったらぜひ、お試しくださいませ。

４．データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Python のコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
ベイズ書籍の実践記録も掲載中です。

最後までお読みいただきまして、ありがとうございました。