
第4章「聞きづらい行為を他のみんなはどれくらいしているか」のベイズモデリングをPyMC Ver.5 で
この記事は、テキスト「たのしいベイズモデリング2」の第4章「聞きづらい行為を他のみんなはどれくらいしているか」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。
テキストは第2章から第4章まで「間接質問法」の各種手法で「違法行為等の経験」の調査データを用いたベイズモデリングに取り組んでいます。
この章では、「Aggregated Response法」(AR法)を用いてデリケートな行為の経験を推論します。
AR法には前書「たのしいベイズモデル」第1章で出会いました。
この当時は自己流モデルの出力がテキストの結果と相違して、苦い思いをしました。
今回の結末はいかに!?
さあ、心新たにPyMCのベイズモデリングを楽しみましょう。
テキストの紹介、引用表記、シリーズまえがき、PyMC等のバージョン情報は、このリンクの記事をご参照ください。
テキストで使用するデータは、R・Stan等のサンプルスクリプトとともに、出版社サイトからダウンロードして取得できます。
サマリー
テキストの概要
執筆者 : 秋山隆 先生、豊田秀樹 先生、久保沙織 先生、岡律子 先生
モデル難易度: ★★★・・ (ふつう)
自己評価
評点
$$
\begin{array}{c:c:c}
実装精度 & ★★・・・ & いまいち \\
結果再現度 & ★・・・・ & NG!! \\
楽しさ & ★★★★・ & 楽しそう \\
\end{array}
$$

評価ポイント
モデル自体の難易度は高くないのですが、PyMCの標準的なクラス・関数を使うだけでは対処のできない「ある部分」が存在し、エラーになってしまいました。
重要なモデルを実装できなかったので、低評価になりました。
工夫・喜び・反省
また一つ、PyMCのある機能の制限を知ることができました。
ただし制限を突破できる代替策には手が届いていません。
また一つ、宿題ができました。

モデルの概要
テキストの調査・実験の概要
■ 間接質問法
間接質問法は、答えにくい質問の回答を得る場合に、回答者のプライバシーを守りつつ、分析に必要なデータを取得できる質問方法です。
テキスト第2章の定義をお借りします。
間接質問法とは、質問する方法を工夫し、調査者が回答結果を見ても各回答者の真の状態はわからないように配慮しつつ、集団の特性について目的とする推定値を得る方法である。
この章の調査では、大学生のデリケートな行為の経験回数・人数(カウントデータ)を取り扱っています。
上記定義に当てはめると、「調査者が回答を見ても大学生個人の回答値が分からないように配慮しつつ、ある大学生グループ全体の推定経験量を得る方法」と言い換えられます。

■ AR法
間接質問法の手法の1つです。
下図をご覧ください。
質問に対して「真の値 ± マスクの値」で回答します。
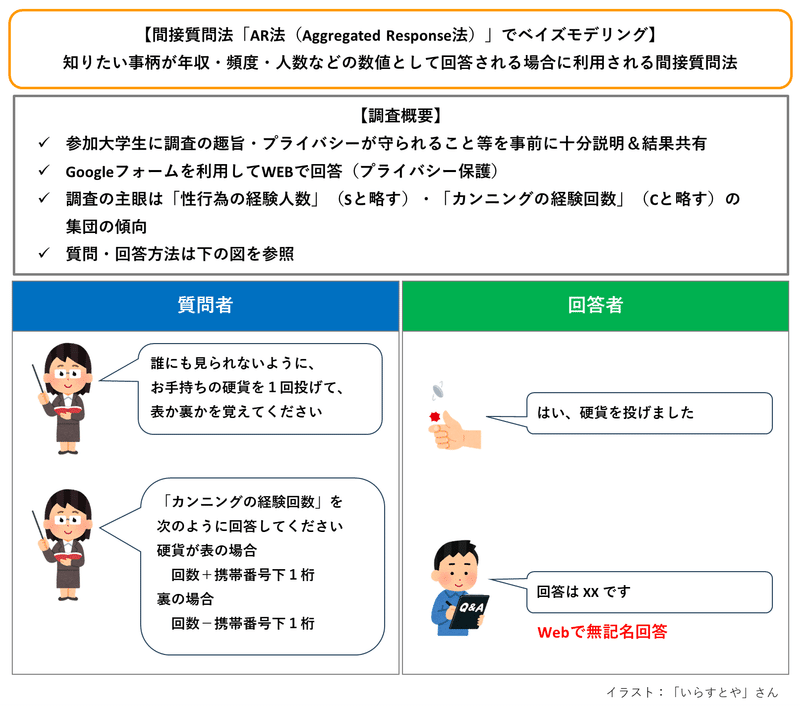
【 例 】
真の経験回数が1回、携帯番号下1桁が5、コインが裏の場合、$${1-5=-4}$$なので回答値は「$${-4}$$」です。
携帯番号下1桁のように、真の値に加減算する数値を「マスク」と呼びます。
マスクは「秘匿(マスク)」となり、プライバシー保護として機能するので、回答者は回答しやすくなります。
■ 調査の概要
「性行為の経験人数」(以下、Sと略します)と「カンニングの経験回数」(以下、Cと略します)を調査項目としています。
Google フォームで質問リストを作成して、調査参加者からWeb上で回答を収集し、Sは130件、Cは125件のデータを用いて分析を進めたそうです。

テキストのモデリング
この章ではモデルの掲載はなく、「たのしいベイズモデリング」第1章を参照するように書かれています。
という事で、「たのしいベイズモデリング」第1章のブログもご参照ください!
「テキストのモデリング」の項に、マスクがモデリングにどのように関わるかを詳しく書いています。
以下のモデリング内容は、「たのしいベイズモデリング」第1章を参考にして書きます。
■目的変数と関心のあるパラメータ
目的変数はマスクされた回答値$${y}$$です。
関心のあるパラメータはマスクを除いた真の人数・回数$${\lambda}$$です。
■ テキストのベイズモデル
テキスト「たのしいベイズモデリング」第1章のモデルを引用いたします。
なお、この章では回答値が平均パラメータ$${\lambda}$$のポアソン分布に従うと仮定されている点を、次の数式に反映しています。
$$
f(y \mid \lambda) = \sum_{k \subset A} \cfrac{1}{N(k \subset A)} f(y-m_k \mid \lambda) \\
$$

■マスク$${m_k}$$、集合$${A}$$、関数$${N(k \subset A)}$$
マスク$${\boldsymbol{m_k}}$$の取りうる値の集合$${\boldsymbol{A}}$$は、回答$${\boldsymbol{y}}$$の値によって変動します。
たとえば回答値$${y=2}$$の場合、加減算する携帯番号下1桁(=マスク)は、コイン裏&下1桁9の$${-9}$$から、コイン表&下1桁2の$${+2}$$までが取りうる値になります。
ではコイン表&下1桁3の場合、どうなるでしょう。
経験人数・回数の最小値が$${0}$$のため回答は$${3}$$以上になってしまい、回答値$${y=2}$$に収まらないのです。
したがって、マスクの値は$${+3}$$以上を取り得ないのです。
まとめますと、回答値$${y=2}$$の場合、マスクの値の集合$${A=\{ -9, -8, \cdots, -1, -0, +0, 1, 2\}}$$となり、要素数$${N(k \subset A)}$$は$${13}$$となります。

■混合分布であること
$${f(y-m_k \mid \quad)}$$は、$${y}$$の値によって変動する集合$${A}$$の要素の数(=マスクの数)だけ、確率分布が存在することを示しています。
回答$${\boldsymbol{y}}$$の値によって、混合する「確率分布の数が変動する」のです!
たとえば$${y=2}$$の場合、混合分布は、以下の$${13}$$個のポアソン分布の確率質量関数を$${1/12}$$づつ均等に混合したものになります。
$$
f(y+9 \mid \lambda) \\
f(y+8 \mid \lambda) \\
\vdots \quad (中略※) \\
f(y+1 \mid \lambda) \\
f(y+0 \mid \lambda) \\
f(y-0 \mid \lambda) \\
f(y-1 \mid \lambda) \\
f(y-2 \mid \lambda) \\
$$
※途中の6つの関数を記載省略
■分析・分析結果
分析の仕方や分析数値はテキストの記述が正確だと思いますので、テキストの読み込みをおすすめします。
PyMCの自己流モデルはエラーが発生して推論できず、分析ができない状況です。

PyMC実装
Let's enjoy PyMC & Python !
準備
1.インポート
### インポート
# ユーティリティ
import pickle
# 数値・確率計算
import pandas as pd
import numpy as np
# PyMC
import pymc as pm
import pytensor.tensor as pt
import arviz as az
# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')
Sのデータ準備
Sの経験人数に関する回答値を確認します。
1.データの読み込み
テキストの R スクリプト内に記述された回答値データを設定します。
### データの読み込み ※Rスクリプト掲載データを昇順ソートしています
data = [-9, -9, -9, -8, -8, -8, -8, -8, -8, -8, -7, -7, -7, -7, -6, -6, -6,
-5, -5, -5, -5, -5, -4, -4, -4, -3, -3, -3, -3, -3, -2, -2, -2, -2, -2,
-1, -1, -1, -1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1,
2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3,
4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 5, 5,
6, 6, 6, 6, 6, 6, 6, 6, 6, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7,
8, 8, 8, 8, 9, 9, 9, 9, 9, 9, 9, 9, 9, 10, 10, 10, 12, 15, 15]
print('標本サイズ: ', len(data))【実行結果】
標本サイズは130です。
2.データの外観の確認
まずは要約統計量を確認します。
### 要約統計量の表示
pd.DataFrame({'回答値(マスク済み)': data}).describe().round(2)【実行結果】
携帯番号下1桁(0から9)でマスクされた回答値です。
最小値の$${-9}$$はマスクの最大値9がマイナスされたものと思われるので、おそらく経験人数は0人でしょう。
最大値の$${+15}$$については、マスクが+9だと経験人数は6人、マスクが-9だと経験人数は24人。

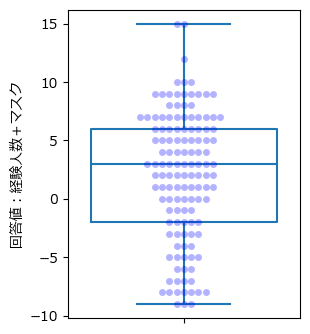
箱ひげ図で可視化してみましょう。
テキストの図4.1に相当します。
### 箱ひげ図の描画 ※図4.1に相当
plt.figure(figsize=(3, 4))
# 箱ひげ図の描画
sns.boxplot(data, color='tab:blue', fill=False)
# スウォームプロットの描画
sns.swarmplot(data, color='blue', alpha=0.3)
plt.ylabel('回答値:経験人数+マスク');【実行結果】
スウォームプロットを重ねてデータ点の分布を見通せるようにしました。
-9から9くらいまで満遍なく分布しているような印象です。
回答値=7が最多回答です。
テキストの表4.1に示された回答値$${y}$$の平均値と標準誤差を計算してみます。
### 平均値と標準誤差の計算 「不偏分散 ÷ 標本サイズ」の平方根 ※表4.1のyに相当
mean1 = np.mean(data)
se1 = np.sqrt(np.var(data, ddof=1) / len(data))
print(f'平均:{mean1:.3f}, 標準誤差:{se1:.3f}')【実行結果】


Sのモデル構築
モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
$$
\begin{align*}
\lambda &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=100) \\
components &= [ \\
&\text{Poisson.dist}\ (\text{mu}=\lambda)-9, \\
&\text{Poisson.dist}\ (\text{mu}=\lambda)-8, \\
&\quad \vdots \\
&\text{Poisson.dist}\ (\text{mu}=\lambda)-0, \\
&\text{Poisson.dist}\ (\text{mu}=\lambda)+0, \\
&\quad \vdots \\
&\text{Poisson.dist}\ (\text{mu}=\lambda)+8, \\
&\text{Poisson.dist}\ (\text{mu}=\lambda)+9, \\
&] \\
likelihood &\sim \text{Mixture}\ (\text{w}=w,\ \text{comp\_dist}=components)\\
\end{align*}
$$
1.初期値設定
混合分布の混合比率$${w}$$を算出します。
回答値$${y}$$の値に応じてマスクの数$${N}$$を求めます。
マスクの取りうる値が$${-9}$$から$${9}$$まで20個あるので、重み$${w}$$の配列は1行あたり20の要素で構成しています。
コードでは、for文で配列の先頭から$${N}$$個までに$${1/N}$$をセットします。
残りの要素は$${0}$$とし、重み0の混合分布が使われないようにします。
### 初期値設定
## データのインデックス、カテゴリ変数のインデックスの取得
idx_data = list(range(len(data)))
## 混合分布の混合比率w:観測データ(全130行)ごとにマスク個数20個分の均等割合を算出
# wの初期化
w = np.zeros((len(data), 20))
# 観測値yごとに可能なマスク個数を算出
num_masks = [y+10 if y<=-1 else y+11 if y<=9 else 20 for y in data]
# w(numpy配列)の作成
for i, num_mask in enumerate(num_masks):
# 配列先頭からマスクの個数までの要素を1/Nにする
w[i, :num_mask] = 1 / num_mask
# wの表示
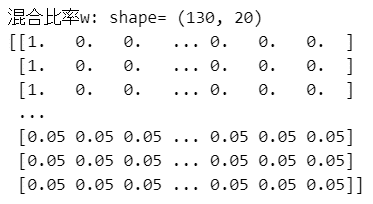
print('混合比率w: shape=', w.shape)
print(w)【実行結果】
混合比率$${w}$$の一部を表示しています。
2.モデルの定義
数式表現を実直にモデル記述します。
ポアソン分布+マスクmはカスタム分布関数 custom_dist で実装しています。
このカスタム分布関数が後に波乱を巻き起こすのです。。。
### モデルの定義
# カスタム分布関数の定義:ポアソン分布+マスクm
def custom_dist(
lam: pt.TensorVariable,
m: pt.TensorVariable,
size: pt.TensorVariable,
) -> pt.TensorVariable:
return pm.Poisson.dist(mu=lam, size=size) + m # ★'+ m'がエラーになる
# モデルの定義
with pm.Model() as model1:
### データ関連定義
# coordの定義
model1.add_coord('data', values=idx_data, mutable=True)
# dataの定義
y = pm.ConstantData('y', value=data, dims='data')
### 事前分布
lam = pm.Uniform('lam', lower=0, upper=100)
### 混合分布に含める確率分布の構成の定義
# マスクのfull集合 [-9, -8, …, 0, 0, …, 9]
masks = np.hstack([np.arange(-9, 1), np.arange(0, 10)])
# リスト内包表記で20個(マスク個数分)のカスタムポアソン分布を生成
components = [
pm.CustomDist.dist(lam, m, dist=custom_dist) for m in masks
]
### 尤度の計算:混合分布
likelihood = pm.Mixture('likelihood', w=w[idx_data], comp_dists=components,
observed=y, dims='data')【モデル注釈】
coordの定義
座標に名前を付けたり、その座標が取りうる値を設定できます。
今回は次の1つを設定しました。データの行の座標:名前「data」、値「行インデックス」
dataの定義
回答値{y}$$を設定しました。パラメータの事前分布
キー項目の内容に関する経験人数$${\lambda}$$の事前分布は区間$${[0,100]}$$の一様分布です。
尤度
20のポアソン分布の混合分布です。
混合分布は次のように実装しました。
尤度likelihoodで 混合分布「pm.Mixture」を指定。
混合分布の構成は「components」を参照。
各分布の重み(混合比率)はwで指定。componentsのリストでは「ポアソン分布+マスクm」を実装するカスタム分布関数「custom_dist」を参照して、リスト内包表記で20個のカスタム分布の確率分布「pm.Custom.dist()」を生成。
カスタム分布関数「custom_dist」では確率分布「ポアソン分布+マスクm」を生成。
3.モデルの外観の確認
# モデルの表示
model1【実行結果】
2行目の混合分布は右が見切れています。
20個のカスタム分布(ポアソン分布+マスク)で構成しています。
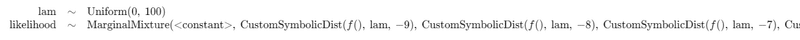
# モデルの可視化
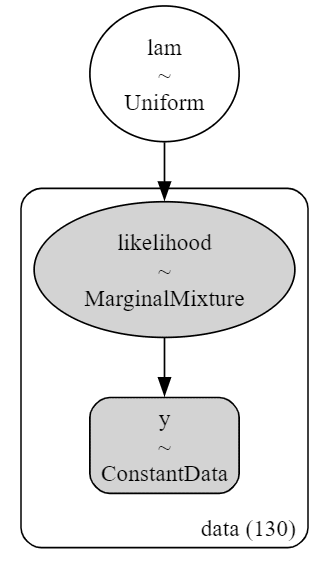
pm.model_to_graphviz(model1)【実行結果】
図はとてもシンプルな構造です。
4.事後分布からのサンプリング
MCMCを実行します。すると・・・
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用
# テキスト:iter=21000, warmup=1000, chains=5
with model1:
idata1 = pm.sample(draws=1000, tune=1000, chains=4, target_accept=0.8,
nuts_sampler='numpyro', random_seed=1234)【実行結果】
謎のエラーが発生しました(泣)
logprobに足し算メソッドが実装されていない、と読むのでしょうか。
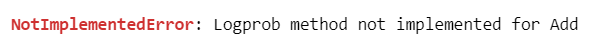

【エラー解析】
モデルのコードを試行錯誤でいじって問題の特定を試みると・・・
カスタム分布関数「custom_dist」で行っている「ポアソン分布+マスクm」(return pm.Poisson.dist(mu=lam, size=size) + m)の「+ m」に問題があるようです。
【試したこと】
・「+m」を外してみた :MCMCでエラーは発生しなかった
return pm.Poisson.dist(mu=lam, size=size)
・正規分布に変更してみた:MCMCでエラーは発生しなかった
return pm.Normal.dist(省略) + m
・二項分布に変更してみた:MCMCでエラーが発生した
return pm.Binomial.dist(省略) + m
推測ではありますが試した結果には、ポアソン分布や二項分布などの離散型分布の場合、カスタム分布の確率分布「pm.Custom.dist()」では加算ができない、という傾向があるように感じます。
原因は分かったものの、対策を見つけることはできませんでした・・・
ポアソン分布を用いたモデリングを断念します。

Cのデータ準備
続いてCのモデリングに進みます。
テキストでは、Cのモデリングを「ポアソン分布」と「正規分布」で行っています。
そこで、PyMCモデリングでは正規分布に取り組もうと思います。
なお、Cの経験回数のAR法では、マスクを「誕生月」としています。
マスクの要素は$${-12, -11, \cdots, -1, 1, -cdots, 11, 12}$$となり、要素数は24です。
1.データの読み込み
テキストの R スクリプト内に記述された回答値データを設定します。
### データの読み込み ※Rスクリプト掲載データを昇順ソートしています
data2 = [-11, -8, -7, -7, -7, -7, -7, -7, -7, -6, -5, -5, -5, -5, -5,
-4, -4, -4, -4, -4, -4, -3, -3, -3, -3, -3, -3, -3,
-2, -2, -2, -2, -2, -1, -1, -1, -1, -1, -1,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1,
2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3,
4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 6, 6, 6, 6, 6, 6, 6, 6,
7, 7, 7, 7, 7, 7, 7, 7, 8, 8, 8, 8, 9, 9, 9, 10, 10, 10, 10,
11, 12, 16, 18, 19, 19, 20, 24]
print('標本サイズ: ', len(data2))【実行結果】
標本サイズは125です。
2.データの外観の確認
まずは要約統計量を確認します。
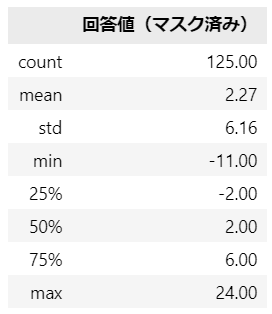
### 要約統計量の表示
pd.DataFrame({'回答値(マスク済み)': data2}).describe().round(2)【実行結果】
誕生月(1から12)でマスクされた回答値です。
最小値の$${-11}$$はマスクのうち11または12がマイナスされたものと思われるので、おそらく経験回数は0回または1回でしょう。
最大値の$${+24}$$については、マスクが+12だと経験回数は12回、マスクが-12だと経験回数は36回。
箱ひげ図で可視化してみましょう。
テキストの図4.6に相当します。
### 箱ひげ図の描画 ※図4.6に相当
plt.figure(figsize=(3, 4))
# 箱ひげ図の描画
sns.boxplot(data2, color='tab:blue', fill=False)
# スウォームプロットの描画
sns.swarmplot(data2, color='blue', alpha=0.3)
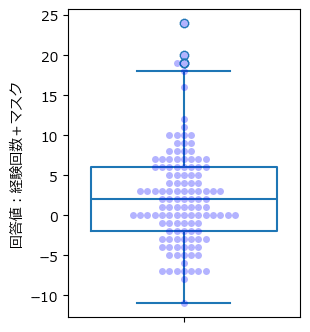
plt.ylabel('回答値:経験回数+マスク');【実行結果】
スウォームプロットを重ねてデータ点の分布を見通せるようにしました。
-8から12くらいまでに概ね収まっていて、ひげの外にはみ出た外れ値的な値も見られます。
回答値=0が最多回答です。
回答値が0になるケースは、マスクが$${-1}$$から$${-12}$$なので、経験回数が$${1}$$から$${12}$$の場合が該当します。
テキストの表4.3に示された回答値$${y}$$の平均値と標準誤差を計算してみます。
### 平均値と標準誤差の計算 「不偏分散 ÷ 標本サイズ」の平方根 ※表4.3のyに相当
mean2 = np.mean(data2)
se2 = np.sqrt(np.var(data2, ddof=1) / len(data2))
print(f'平均:{mean2:.3f}, 標準誤差:{se2:.3f}')【実行結果】
平均$${2.272}$$は従来法による経験回数の推定値です。


Cのモデル構築
続いて、Sのモデルを転用してC用にアレンジします。
モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
ポアソン分布に代えて正規分布を用いています。
$$
\begin{align*}
\mu &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=100) \\
\sigma &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=100) \\
components &= [ \\
&\text{Normal.dist}\ (\text{mu}=\mu,\ \text{sigma}=\sigma)-12, \\
&\text{Normal.dist}\ (\text{mu}=\mu,\ \text{sigma}=\sigma)-11, \\
&\quad \vdots \\
&\text{Normal.dist}\ (\text{mu}=\mu,\ \text{sigma}=\sigma)-1, \\
&\text{Normal.dist}\ (\text{mu}=\mu,\ \text{sigma}=\sigma)+1, \\
&\quad \vdots \\
&\text{Normal.dist}\ (\text{mu}=\mu,\ \text{sigma}=\sigma)+11, \\
&\text{Normal.dist}\ (\text{mu}=\mu,\ \text{sigma}=\sigma)+12, \\
&] \\
likelihood &\sim \text{Mixture}\ (\text{w}=w,\ \text{comp\_dist}=components)\\
\end{align*}
$$
1.初期値設定
混合分布の混合比率$${w}$$を算出します。
回答値$${y}$$の値に応じてマスクの数$${N}$$を求めます。
マスクの取りうる値が$${-12}$$から$${12}$$まで24個あるので、重み$${w}$$の配列は1行あたり24の要素で構成しています。
コードでは、for文で配列の先頭から$${N}$$個までに$${1/N}$$をセットします。
残りの要素は$${0}$$とし、重み0の混合分布が使われないようにします。
### 初期値設定
## データのインデックス、カテゴリ変数のインデックスの取得
idx_data = list(range(len(data2)))
## 混合分布の混合比率w:観測データ(全125行)ごとにマスク個数24個分の均等割合を算出
# wの初期化
w = np.zeros((len(data2), 24))
# 観測値yごとに可能なマスク個数を算出
num_masks = [y+13 if y<=-1 else y+12 if y<=12 else 24 for y in data2]
# w(numpy配列)の作成
for i, num_mask in enumerate(num_masks):
# 配列先頭からマスクの個数までの要素を1/Nにする
w[i, :num_mask] = 1 / num_mask
# wの表示
print('混合比率w: shape=', w.shape)
print(w)【実行結果】
混合比率$${w}$$の一部を表示しています。

2.モデルの定義
### モデルの定義 正規分布モデル
# カスタム正規分布関数の定義:正規分布+マスクm ※ +mの妥当性に自信がない
def custom_dist(
mu: pt.TensorVariable,
sigma : pt.TensorVariable,
m: pt.TensorVariable,
size: pt.TensorVariable,
) -> pt.TensorVariable:
return pm.Normal.dist(mu=mu, sigma=sigma, size=size) + m # '+ m'
# モデルの定義
with pm.Model() as model3:
### データ関連定義
# coordの定義
model3.add_coord('data', values=idx_data, mutable=True)
# dataの定義
y = pm.ConstantData('y', value=data2, dims='data')
### 事前分布
mu = pm.Uniform('mu', lower=0, upper=100)
sigma = pm.Uniform('sigma', lower=0, upper=100)
### 混合分布に含める確率分布の構成の定義
# マスクの集合 [-12, -1, …, -1, 1, …, 12]
masks = np.delete(np.arange(-12, 13), 12)
# リスト内包表記で24個(マスク個数分)のカスタム正規分布を生成
components = [
pm.CustomDist.dist(mu, sigma, m, dist=custom_dist) for m in masks
]
### 尤度の計算:混合分布
likelihood = pm.Mixture('likelihood', w=w, comp_dists=components,
observed=y, dims='data')【モデル注釈】
coordの定義
座標に名前を付けたり、その座標が取りうる値を設定できます。
今回は次の1つを設定しました。データの行の座標:名前「data」、値「行インデックス」
dataの定義
回答値{y}$$を設定しました。パラメータの事前分布
キー項目の内容に関する経験回数の平均$${\mu}$$と標準偏差$${\sigma}$$の事前分布は、区間$${[0,100]}$$の一様分布です。
尤度
24の正規分布の混合分布です。
混合分布は次のように実装しました。
尤度likelihoodで 混合分布「pm.Mixture」を指定。
混合分布の構成は「components」を参照。
各分布の重み(混合比率)はwで指定。componentsのリストでは「正規分布+マスクm」を実装するカスタム分布関数「custom_dist」を参照して、リスト内包表記で24個のカスタム分布の確率分布「pm.Custom.dist()」を生成。
カスタム分布関数「custom_dist」では確率分布「正規分布+マスクm」を生成。
3.モデルの外観の確認
# モデルの表示
model3【実行結果】
2行目の混合分布は右が見切れています。
24個のカスタム分布(正規分布+マスク)で構成しています。
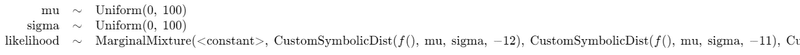
# モデルの可視化
pm.model_to_graphviz(model3)【実行結果】
隠れミッキーがいます!?
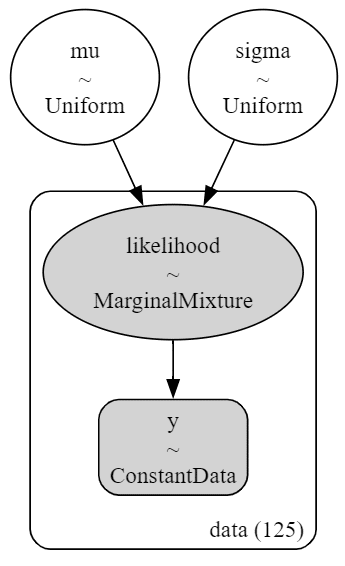
4.事後分布からのサンプリング
乱数生成数はテキストと同じです。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
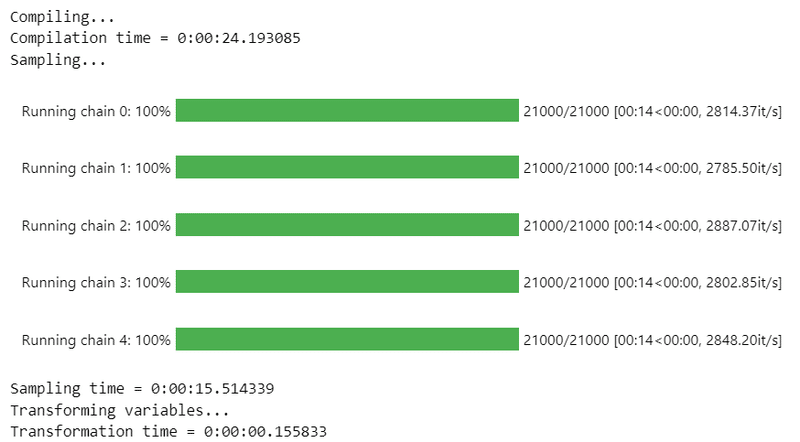
処理時間はおよそ50秒でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 50秒
# テキスト:iter=21000, warmup=1000, chains=5
with model3:
idata3 = pm.sample(draws=20000, tune=1000, chains=5, target_accept=0.8,
nuts_sampler='numpyro', random_seed=1234)【実行結果】
エラーなくMCMCを実行することができました!
5.サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$とします。
### r_hat>1.1の確認
# 設定
idata_in = idata3 # idata名
threshold = 1.01 # しきい値
# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum())【実行結果】
ひとまず、しきい値を$${\hat{R} > 1.01}$$で確認しました。
$${\hat{R} > 1.01}$$のパラメータは「0」件です。
全てのパラメータが$${\hat{R} \leq 1.01}$$であることを確認できました。

ざっくり事後分布サンプリングデータの要約統計量とトレースプロットを確認します。
### 推論データの要約統計情報の表示
pm.summary(idata3, hdi_prob=0.95, round_to=3)【実行結果】
Cの経験回数の平均$${\mu}$$の平均値(テキストのEAP)は5.339です。

### トレースプロットの表示
pm.plot_trace(idata3, compact=False)
plt.tight_layout();【実行結果】
右のグラフはまんべんなく描画されていて、収束している感じがします。
左のグラフの5つの色=5本のマルコフ連鎖chainは重なっていて、ほぼ同一の推論値をはじき出しています。
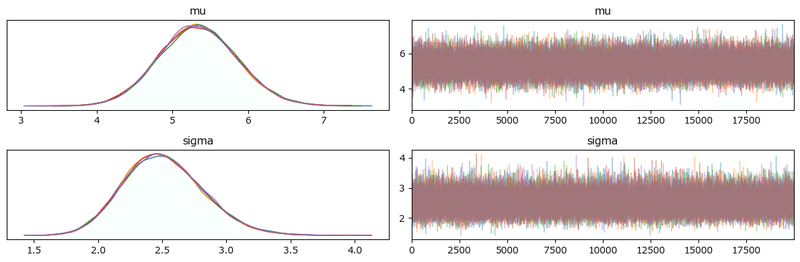
平均パラメータ$${\mu}$$と標準偏差パラメータ$${\sigma}$$の事後分布を可視化しましょう。
事後分布サンプリングデータでヒストグラムを描画します。
seaborn の histplot でKDE曲線付きのグラフを作成します。
### パラメータの事後分布の可視化
# 描画領域の設定
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 4), sharey=True)
# μのヒストグラムの描画
sns.histplot(idata3.posterior.mu.data.flatten(), bins=30, kde=True,
stat='density', color='steelblue', edgecolor='white', alpha=0.5,
ax=ax1)
ax1.set(title='μの事後分布', xlabel='μ', ylabel='density')
# σのヒストグラムの描画
sns.histplot(idata3.posterior.sigma.data.flatten(), bins=30, kde=True,
stat='density', color='tomato', edgecolor='white', alpha=0.5,
ax=ax2)
ax2.set(title='σの事後分布', xlabel='σ')
# 最終化
plt.tight_layout()
plt.show()【実行結果】
美しいベル型です!
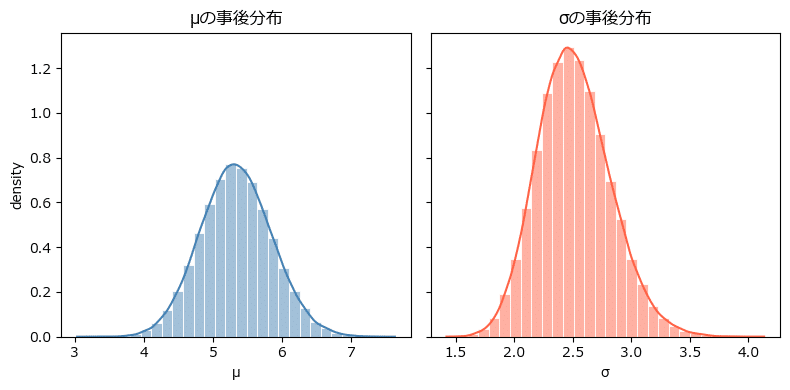

分析
Cの経験回数について、正規分布モデルの事後分布に基づいて分析を進めます。
分析~テキストにならって
平均$${\mu}$$と標準偏差$${\sigma}$$の事後統計量を表示します。
テキストの表4.4に相当します。
### 推論データの事後統計量の算出 ※表4.4に相当
# 要約統計量計算関数の定義
def calc_stats(x):
ci = np.quantile(x, q=[0.025, 0.975])
hdi = az.hdi(x, hdi_prob=0.95)
return np.mean(x), np.std(x), ci[0], ci[1], hdi[0], hdi[1]
# 要約統計量データフレームの作成
stats_df2 = pd.DataFrame(
{'μ': calc_stats(idata3.posterior.mu.data.flatten()),
'σ': calc_stats(idata3.posterior.sigma.data.flatten())},
index = ['EAP', 'post.sd', 'CI2.5%', 'CI97.5%', 'HDI2.5%', 'HDI97.5%']
).T
# データフレームの表示
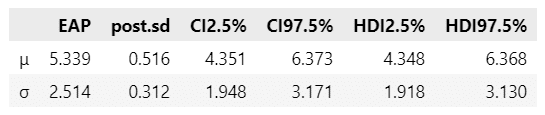
display(stats_df2.round(3))【実行結果】
テキストとほぼ同じ結果になりました!
【分析】
平均パラメータ$${\mu}$$の平均値(EAP)は$${5.339}$$、事後標準偏差(post.sd)は$${0.516}$$です。
点推定・区間推定を比較します。
ポアソン分布の値はテキストからの引用です。
$$
\begin{array}{c|ccc}
モデル & 平均値 & 標準偏差・誤差 & 95\%CI下側 & 95\%CI上側 \\
\hline
正規分布 & 5.339 & 0.516 & 4.351 & 6.373 \\
ポアソン分布 & 5.007 & 0.536 & 3.975 & 6.076 \\
従来法 & 2.272 & 0.551 & - & - \\
\end{array}
$$
平均値に関して
正規分布モデルとポアソン分布モデルは同程度です。
一方で、2つのモデルと従来法の推定値はかけ離れています。
従来法の平均値$${2.272}$$は、正規分布モデル・ポアソン分布モデルの95%CIの区間に含まれていません。
標準偏差・誤差・95%信用区間に関して
正規分布モデル・ポアソン分布モデルの標準偏差は、従来法の標準誤差$${0.551}$$よりも小さくなっています。
正規分布モデルの標準偏差、95%信用区間の幅は、ポアソン分布モデルよりも小さくて狭いです。
続いてPHC曲線を描画します。
テキストの図4.7に相当し、正規分布モデルを仮定した上での「Cの経験回数の平均が$${c}$$よりも大きい」という研究仮説が正しい確率の曲線です。
まずPHC曲線の描画関数を定義します。
### 推論データidataを受け取ってPHC曲線を描画する関数
def phc_plot(data):
## データ加工
# x軸目盛値となるcの値を生成
x = np.linspace(0, 10, 1001)
# μ > c の割合を計算
y = [(data > c).sum() / len(data) for c in x]
## 描画処理:描画結果をaxに格納
plt.plot(x, y)
plt.xlabel('c')
plt.ylabel('確率:PHC')PHC曲線を描画します。
### PHC曲線の描画 ※図4.7に相当
plt.figure(figsize=(6, 4))
phc_plot(idata3.posterior.mu.data.flatten()) # 上記描画関数にμの事後sampleを渡す
plt.title(f'「平均値 μ > c 」の確率:PHC曲線')
plt.legend(['経験回数のPHC'])
plt.grid(lw=0.3);【実行結果】
テキストとほぼ同じ結果を得られました。
4回以上6回以下の間で確率が大きく変動(急降下)していることが分かります。
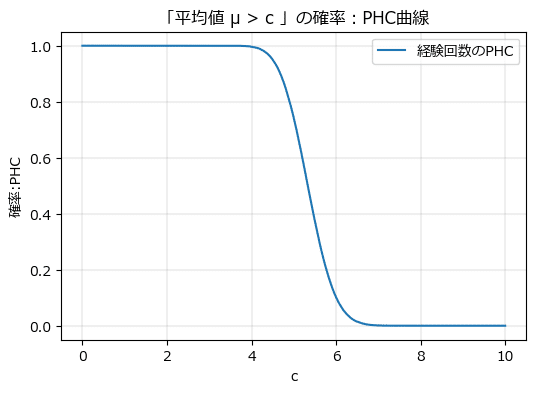
経験回数の平均が 4 より大きい($${p>4}$$)というPHC、6 より大きい($${p>6}$$)というPHCを計算してみます。
### Cの経験回数の平均が4より大きい(p>4)というPHCの算出
p = idata3.posterior.mu.data.flatten()
c = 4
print(f'p > {c}の確率: {(p > c).sum() / len(p):.1%}')【実行結果】
4回を上回る確率はほぼ100%です。
Cの経験の集団平均は、少なくとも4回はありそうです。

### Cの経験回数の平均が6より大きい(p>6)というPHCの算出
p = idata3.posterior.mu.data.flatten()
c = 6
print(f'p > {c}の確率: {(p > c).sum() / len(p):.1%}')【実行結果】
6回を上回る確率は小さくなりました。


最後に、推論データを再利用する場合に備えてファイルに保存しましょう。
idataをpickleで保存します。
### idataの保存 pickle
file = r'idata3_ch04.pkl'
with open(file, 'wb') as f:
pickle.dump(idata3, f)読み込みコードは次のとおりです。
### idataの読み込み pickle
file = r'idata3_ch04.pkl'
with open(file, 'rb') as f:
idata3_load = pickle.load(f)以上で第4章は終了です。
おわりに
3つの間接質問法記事の起源
第2~4章で3つの間接質問法の手法に取り組みました。
個人的には第3章のランダム回答法がシンプルで分かりやすかったです。
ただランダム回答法が適用できるのは回答値が2値の場合のようです。
カウントデータや連続値なども扱えるシンプルな方法(アイテムカウント法・AR法以外)は無いものかと、Web検索していたら・・・
次のサイトを発見しました!
第2~4章の執筆者の顔ぶれも。
当時はベイズを利用していなかったようです。
ご参考まで。

シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
この記事が気に入ったらサポートをしてみませんか?
