今回の統計トピック

統計的仮説検定の「第１種の過誤」を深掘りします。
帰無仮説を棄却することが抱えるリスクに接近しましょう！

公式問題集の準備

「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください！
「知る」「実践する」の章で、のんびり統計をお楽しみください！

問題を解く

📘公式問題集のカテゴリ

検定の分野
問2 第１種の過誤・確率（画鋲投げ）

試験実施年月
調査中

問題

公式問題集をご参照ください。

解き方

題意
与えられた帰無仮説と棄却条件から、第１種の過誤の内容と確率を求める問題です。

図示します。

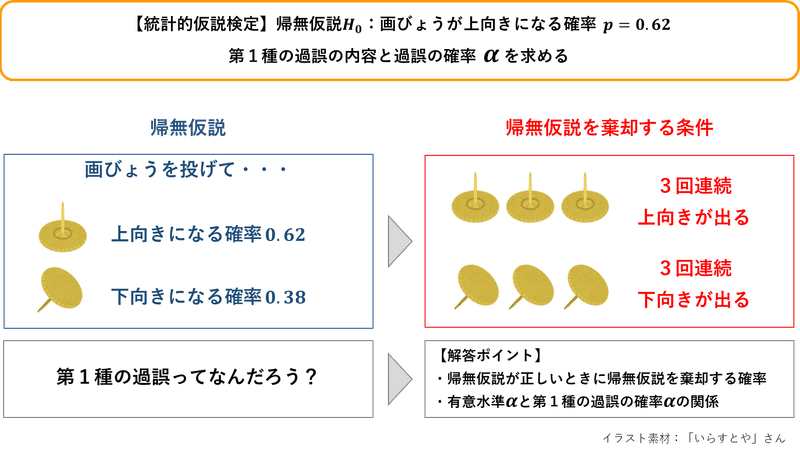
統計的仮説検定と誤り

統計的仮説検定は、確率の考え方を用いて仮説の採用／不採用を判断します。
例えば、標本データから得た検定統計量の確率が十分小さいことを確認して、母集団に関する帰無仮説を棄却するような考え方です。

ただし、十分小さい確率を用いたとしても、母集団に関する判断を誤ることがあります。
小さな確率の方に正解を含んでいるかもしれないからです。
母集団の正解値が明白でない状況での判断であり、統計的仮説検定による選択には誤りを含む可能性があるのです。

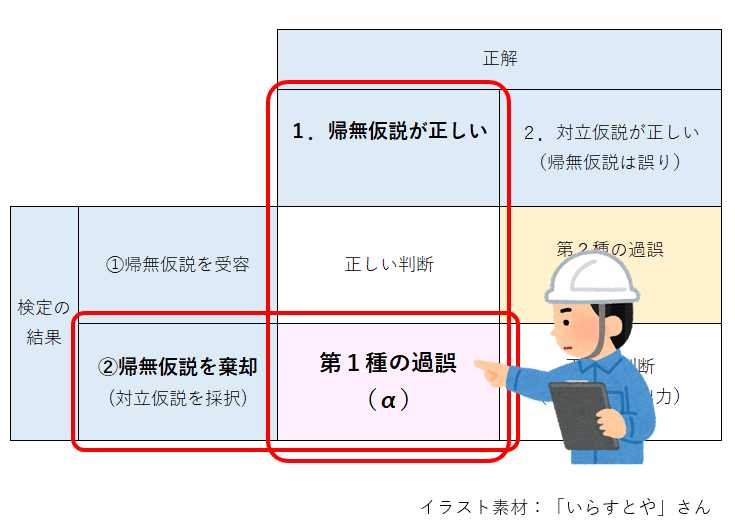
誤りには「第１種の過誤」と「第２種の過誤」があります。
第１種の過誤は「帰無仮説が正しいときに帰無仮説を棄却する誤り」です。

第１種の過誤の解答

問題文の言葉に置き換えます。
・帰無仮説は$${p=0.62}$$
・帰無仮説を棄却する条件は、3回連続で画びょうが上を向く、または、3回連続で画びょうが下を向く
です。

第１種の過誤の解答は、「帰無仮説$${p=0.62}$$が正しいときに、3回連続で画びょうが上を向くか、3回連続で画びょうが下を向いて、帰無仮説を棄却する誤り」となります。

第１種の過誤を犯す確率

第１種の過誤の解答のとおり、「帰無仮説が正しいときに、3回連続で画びょうが上を向くか、3回連続で画びょうが下を向いて、帰無仮説を棄却する」ことが、第１種の過誤を犯す要因になります。
そして、第１種の過誤を犯す確率は、「帰無仮説が正しいときに、3回連続で画びょうが上を向くか、3回連続で画びょうが下を向く確率」ということになります。

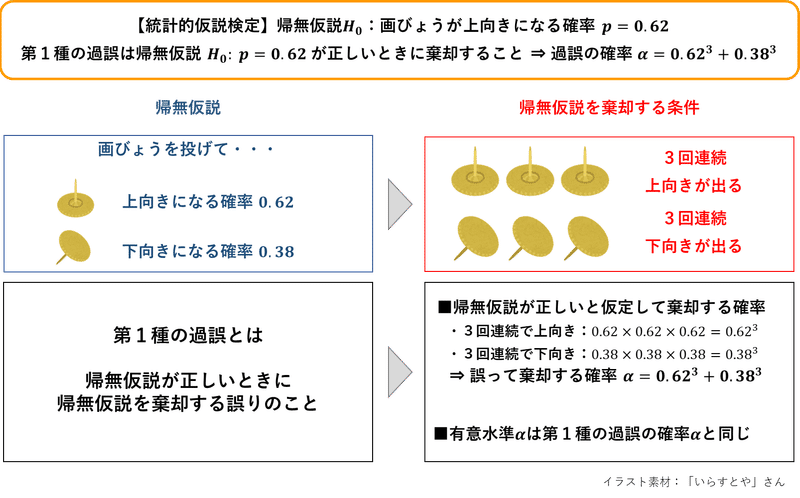
第１種の過誤を犯す確率の解答

「帰無仮説が正しいときに、3回連続で画びょうが上を向くか、3回連続で画びょうが下を向く確率」を計算しましょう。

帰無仮説が正しいとは、画びょうが上を向く確率$${p=0.62}$$ということです。
裏返すと、画びょうが下を向く確率は$${1-0.62=0.38}$$です。

3回連続で画びょうが上を向く確率は、$${0.62 \times 0.62 \times 0.62=0.62^3}$$です。
3回連続で画びょうが下を向く確率は、$${0.38 \times 0.38 \times 0.38=0.38^3}$$です。
よって、「帰無仮説が正しいと仮定したときに、3回連続で画びょうが上を向くか、3回連続で画びょうが下を向く確率」は$${0.62^3 + 0.38^3=0.2932}$$です。

第１種の過誤を犯す確率の解答は、$${0.62^3 + 0.38^3=0.2932}$$です。

二項分布で棄却する確率を確認する

「帰無仮説$${H_0}$$：上を向く確率$${p=0.62}$$」の画びょうを投げる試行を$${n=3}$$回行って、上を向く回数を$${x}$$とします。
上を向く回数$${x}$$の確率は、二項分布$${Bin(3, 0.62)}$$の確率$${P(x \mid H_0)=\ _3C_x\times 0.62^x \times 0.38^{3-x}}$$になるでしょう。

そこで、二項分布を可視化して、棄却条件＝棄却域を確認してみましょう。

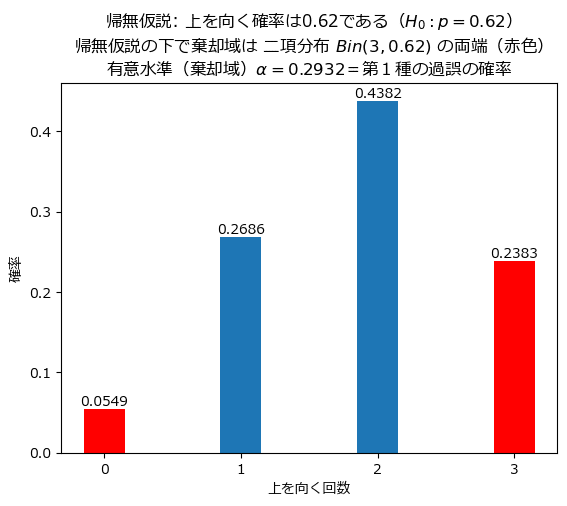
赤色の棒が、上を向く回数が0回（3回連続下向き）と、3回（3回連続上向き）にあたります。
棒の上の値が各回数の確率です。
赤色の棄却域＝第１種の過誤の確率$${\alpha}$$は合計で0.2932です。

問題では、赤色の領域の起きる確率が小さいものとして、棄却条件を設定していると思われます。

シミュレーションで第１種の過誤を体感する

上向きになる確率$${p=0.62}$$が正しいとき、３回連続で上向き／下向きになる確率は、実際のところ、問題集の通り（上の二項分布の確率の通り）になるのでしょうか？

Pythonで実験してみましょう。
一様分布に従う０以上１未満の乱数を３つ生成します。
乱数が0.62以下の場合を上向き、0.62超の場合を下向きとします。
例えば、乱数が「0.5、0.8、0.2」のとき、「上向き、下向き、上向き」です。

まず、３回投げる試行を１回やってみます。

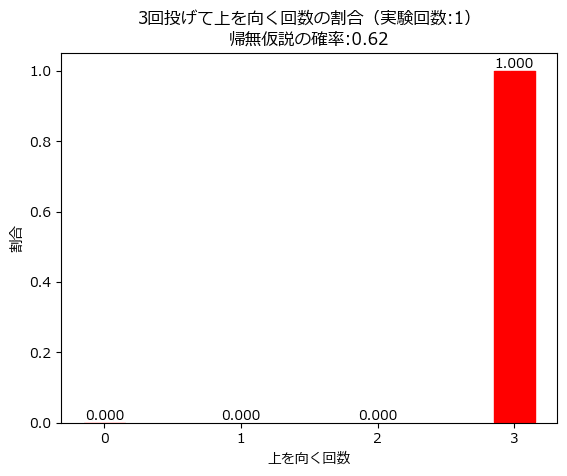
いきなり３回連続上向きが出てしまいました。
帰無仮説：上向きになる確率$${p=0.62}$$は棄却されます！
上向きになる確率が$${1}$$のとき、３回連続上向きになる確率が$${1^3=1}$$になります。

どうやら第１種の過誤が発動したようです。

続いて、３回投げる試行を１０回実験します。

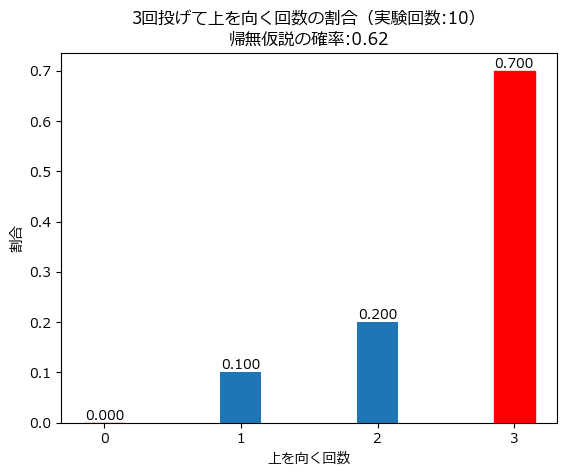
10回の実験中、7回も３回連続上向きになりました。
確率が$${0.888}$$のとき、３回連続上向きになる確率が$${0.888^3 \fallingdotseq 0.7}$$になります。
上向きになる確率は$${0.62}$$よりも大きいのでは？と疑いたくなります。
おそらく、「上向きになる確率は$${0.62}$$」は棄却されるでしょう。

ここでも第１種の過誤が発動したようです。

実験回数を10,000回に増量しましょう。

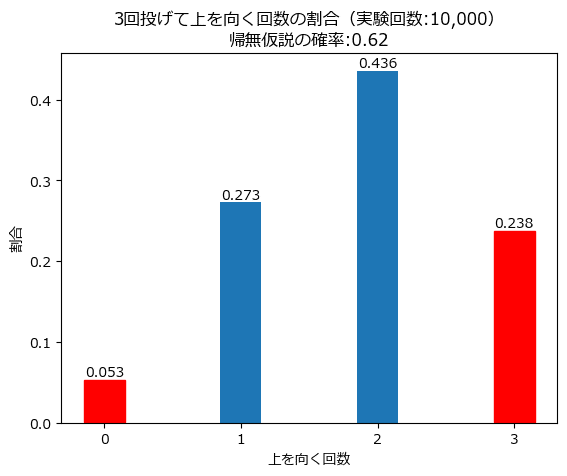
最初のグラフである二項分布$${Bin(3, 0.62)}$$にかなり近づきました。
実験回数を大きくすることで、上向きになる確率が$${0.62}$$の二項分布に近似することが分かりました。

シミュレーションを通じて、「『偶然』レアな事象が起きてしまって、本当は帰無仮説の確率$${0.62}$$が正しいのに、帰無仮説を棄却してしまうこと」を体感できたかと思います。

統計的仮説検定は、母集団の正解が分からないがゆえ、標本データを介して母集団の様子を確かめる手続きです。
しかし、標本データが偶然、レアな事象に該当する可能性を完全に抑え込むことはできず、帰無仮説が母集団の正しい仮説であっても、棄却してしまう可能性があります。
統計的仮説検定は第１種の過誤の危険をはらんでいるのです。

解答

② です。

難易度　やさしい

・知識：第１種の過誤、棄却域、確率計算
・計算力：電卓（低）
・時間目安：1分

知る

おしながき

公式問題集の問題に接近してみましょう！
今回は、統計的仮説検定の流れに乗って２つの過誤を見ていきましょう。

統計的仮説検定

📕公式テキスト：4.2.4 棄却と受容、２種類の誤り（140ページ～）

統計的仮説検定の判断の概要

まず帰無仮説と対立仮説を立てます。
そして、①観測したデータから得られた量を調べます。
この量を調べて、②帰無仮説が正しいと仮定した上で、確率的に「滅多に起きないレアなことが起きている」と判明したとします。
この場合、「帰無仮説が正しいならば滅多に起きない（発生確率が小さい）ことが、『現実に』起きています。偶然に起きたのではなく帰無仮説が正しくないと考えるのが適切でしょう」と考えます。
結論として、③帰無仮説を取り下げます。

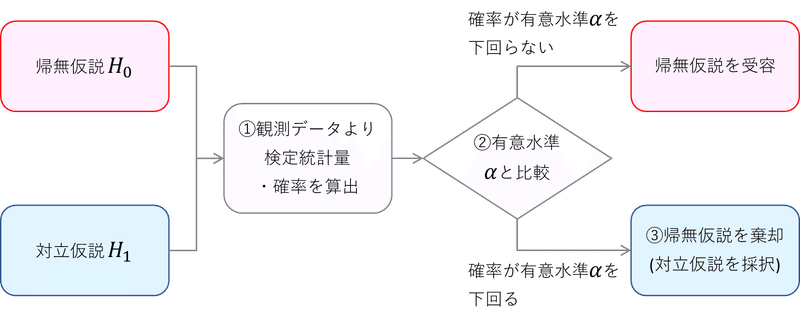
要約します。
帰無仮説が正しいと仮定したときに、①検定統計量の確率を求めて、②有意水準を下回る場合、③帰無仮説を棄却します。

第１種の過誤

統計的仮説検定の判断には「本当は帰無仮説が正しいのに、検定統計量の確率が偶然、有意水準を下回ったため、帰無仮説を棄却する誤り」を含んでいます。
この誤りを「第１種の過誤」と呼びます。

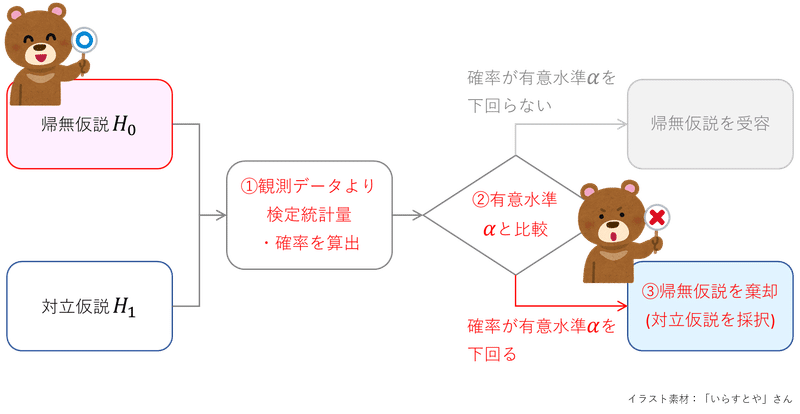
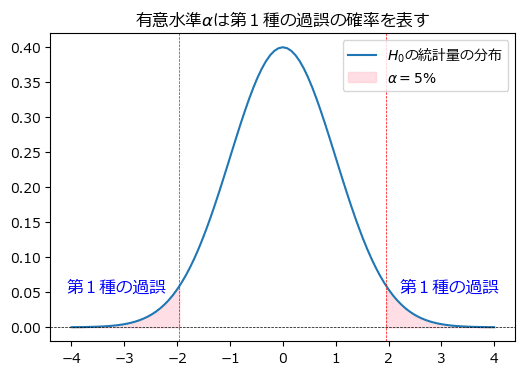
第１種の過誤の可視化（例）

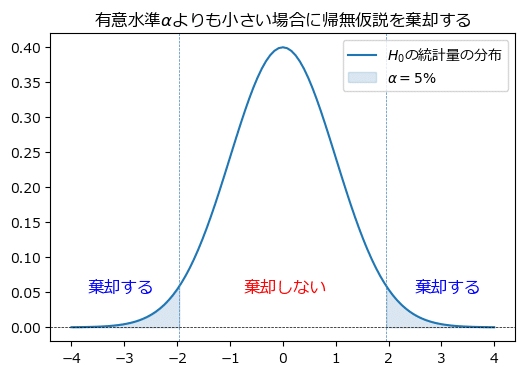
標本から算出する検定統計量が標準正規分布に従う場合、有意水準$${\alpha}$$＝第１種の過誤の確率は、正規分布の両端（下側・上側）の確率を用います。
グラフの両端の赤塗りの部分が$${\alpha}$$に相当します。

第１種の過誤と第２種の過誤

第１種があるということは・・・
第２種の過誤もあります。
第２種の過誤は「対立仮説が正しいときに帰無仮説を受容する誤り」です。
表にまとめます。

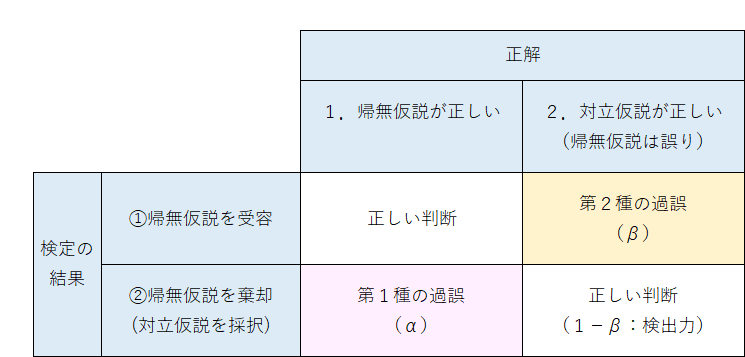
第１種の過誤と第２種の過誤の関係

２つの過誤を可視化してみましょう。
片側検定、標準正規分布の例です。
帰無仮説は青い曲線、対立仮説はオレンジの曲線です。

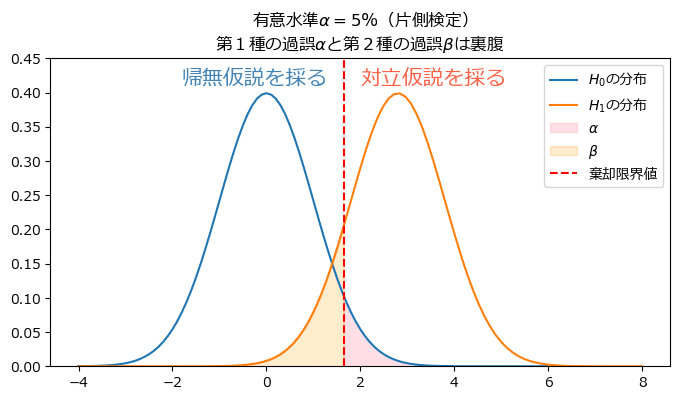
赤い点線が棄却限界値を示しています。
赤い点線の両側に注目しましょう。
赤塗りが、第１種の過誤の確率$${\alpha}$$＝有意水準に相当します。
反対側の黄色塗りが、第２種の過誤の確率$${\beta}$$に相当します。

有意水準の値を小さくする＝第１種の過誤の確率を小さくすることは、赤い点線を右側にずらして、赤塗りの領域を小さくすることです。
そうすると、黄色塗りの領域が大きくなるので、第２種の過誤の確率が大きくなります。

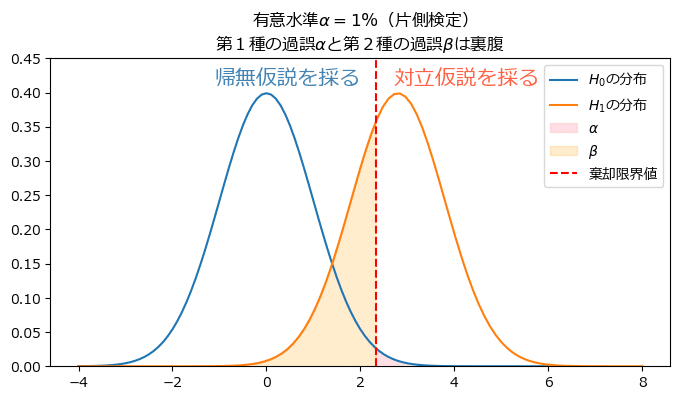
逆に、有意水準の値を大きくする＝第２種の過誤の確率を小さくすることは、赤い点線を左側にずらして、黄色塗りの領域を小さくすることです。
そうすると、赤塗りの領域が大きくなるので、第１種の過誤の確率が大きくなります。

第１種の過誤の危険と第２種の過誤の危険はトレードオフの関係にあるのです。

実践する

Pythonで実験してみよう！

今回は「問題を解く」の章で用いた「第１種の過誤のシミュレーション」をPythonで動かして第１種の過誤が発現する様子を確認しましょう。

電卓・手作業で作成してみよう！

今回はお休みです。

EXCELで作成してみよう！

今回はお休みです。

Pythonで作成してみよう！

プログラムコードを読んで、データを流したりデータを変えてみたりして、データを追いかけることで、作表ロジックを把握する方法も効果的でしょう。
サンプルコードを揃えておけば、類似する作表作業を自動化して素早く結果を得ることができます。

今回は、第１種の過誤のシミュレーションを実施します。

①インポート

import numpy as np
from scipy.stats import norm, binom, t
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'

②シミュレーション関数の定義

「一様分布の乱数」と「上向きの確率」を用いて、上向きかどうかを判定します。
引数は次のとおりです。

def simulator(n, p, num_trial, random_seed=2):
    
    ### 初期値設定
    counter = np.zeros(n+1)      # 上向き回数0～nの度数カウンタを0で初期化
    np.random.seed(random_seed)  # 乱数シード

    ### 投げるシミュレーション
    # n回投げて上向き回数をカウント
    # 実験回数num_trial分、繰り返す
    
    for trial in range(num_trial):
        # n個乱数を生成。上向き確率p以下を上向き（True）とする
        throw = [np.random.rand() <= p for _ in range(n)]
        # 上向き（True）回数を合計して、上向き回数の度数カウンタを1upする
        counter[sum(throw)] += 1        
    
    # 上向き回数の相対度数を計算
    proportion = counter / num_trial
    
    ### プロット
    # 上向き回数の相対度数を描画
    x_ticks = np.arange(n+1)
    g1 = plt.bar(x_ticks, proportion, width=0.3)
    g1[0].set_color('red'),         # 0回とn回の棒を赤色にする
    g1[-1].set_color('red')
    plt.bar_label(g1, fmt='%.3f')   # 相対度数を表示
    # 修飾
    plt.xticks(x_ticks)
    plt.title(f'{n}回投げて上を向く回数の割合（実験回数:{num_trial:,}）\n'
              f'帰無仮説の確率:{p}')
    plt.xlabel('上を向く回数')
    plt.ylabel('割合')
    plt.show()

シミュレーション１：実験回数１回
３回投げる実験を１回実施します。上向きの確率は$${0.62}$$です。
まずは乱数シードをデフォルト値「2」で実施します。

# 設定 n:１度の実験で投げる回数、p：上向きの確率、num_trial：実験回数
n, p, num_trial = 3, 0.62, 1

# シミュレーションの実行
simulator(n, p, num_trial)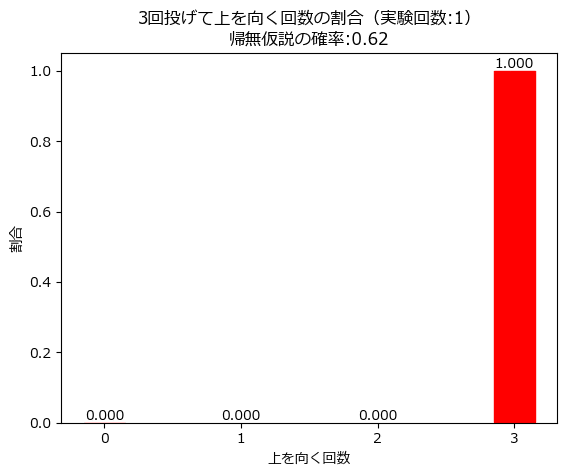

３回上向きになりました。

乱数シードを別の値にしてみましょう。

# 設定 n:１度の実験で投げる回数、p：上向きの確率、num_trial：実験回数
n, p, num_trial = 3, 0.62, 1
random_seed = 1    # 乱数シードを設定

# シミュレーションの実行
simulator(n, p, num_trial, random_seed)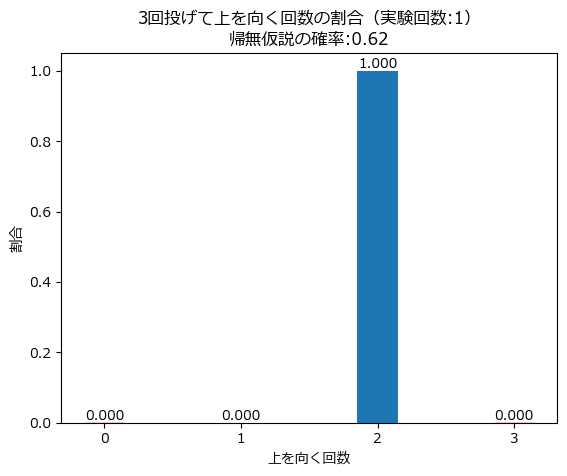

２回上向きになりました。
乱数シードの選択によって結果が変わってしまいます。

シミュレーション２：実験回数１０回
まずは乱数シードをデフォルト値「2」で実施します。

# 設定 n:１度の実験で投げる回数、p：上向きの確率、num_trial：実験回数
n, p, num_trial = 3, 0.62, 10

# シミュレーションの実行
simulator(n, p, num_trial)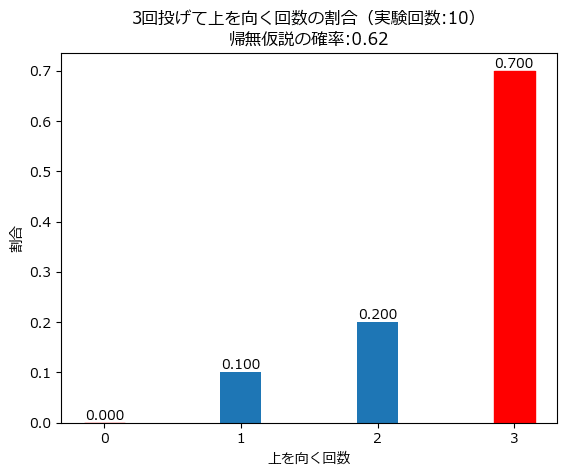

３回連続で上向きになる確率が高いです。
上向きになる確率が$${p=0.62}$$とは言いがたいほどの偏りです。

乱数シードを別の値にしてみましょう。

# 設定 n:１度の実験で投げる回数、p：上向きの確率、num_trial：実験回数
n, p, num_trial = 3, 0.62, 10
random_seed = 1    # 乱数シードを設定

# シミュレーションの実行
simulator(n, p, num_trial, random_seed)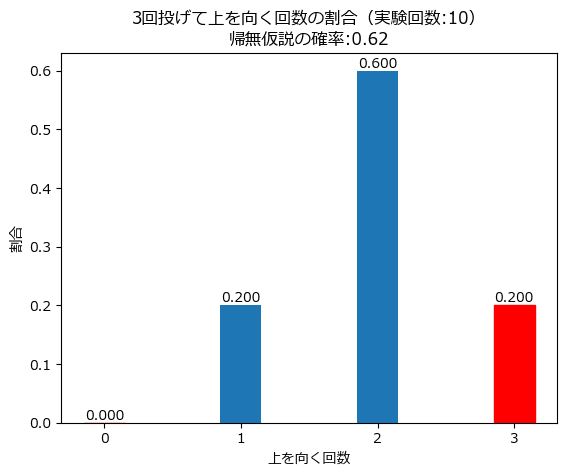

まあまあの結果になりました。
実験回数が少ないとき、乱数シードの設定が結果に大きく影響することが分かりました。

シミュレーション２：実験回数１万回
実験回数を増やしましょう。
乱数シードは「2」です。

# 設定 n:１度の実験で投げる回数、p：上向きの確率、num_trial：実験回数
n, p, num_trial = 3, 0.62, 10000

# シミュレーションの実行
simulator(n, p, num_trial)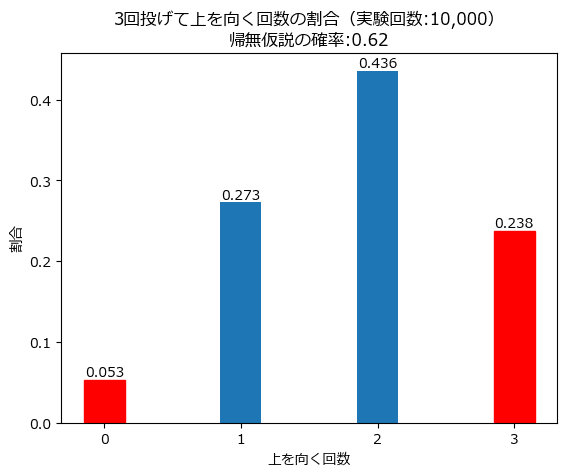

実験回数を大きくすると、二項分布$${Bin(n, p)}$$の姿に近似してきます。

その他の実験
上向きになる確率を$${0.8}$$にして、１０回投げて上向きの回数を数える実験を１万回繰り返します。

# 設定 n:１度の実験で投げる回数、p：上向きの確率、num_trial：実験回数
n, p, num_trial = 10, 0.8, 10000

# シミュレーションの実行
simulator(n, p, num_trial)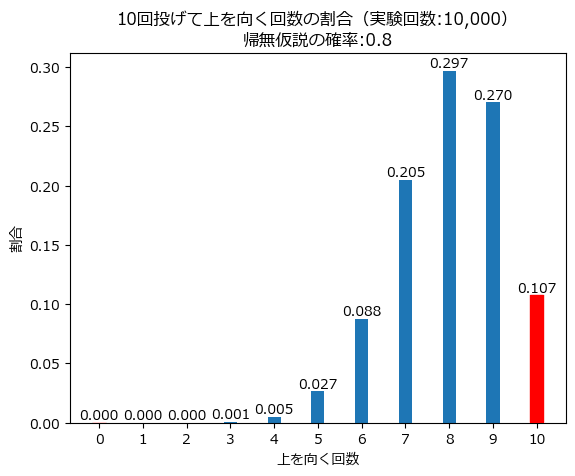

おそらく二項分布$${Bin(10,0.8)}$$に近似していると思われます。

ブログ上の実験は以上です。
確率や回数をさまざまな値に変えて、実験してみてくださいね。

Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。

おわりに

有意水準$${\alpha}$$が第１種の過誤の確率に等しいことが分かりました。
確率を用いて判断する統計的仮説検定の特徴です。

最後までお読みいただきまして、ありがとうございました。

のんびり統計シリーズの記事

次の記事

前の記事

目次