この記事は、テキスト「RとStanではじめる 心理学のための時系列分析入門」の第２章「時系列分析の基本操作」のRスクリプトをお借りして、Pythonで「実験的」に実装する様子を描いた統計ドキュメンタリーです。

取り扱いテーマは次の基礎編です。
・自己相関
・変動分解
・ARモデル、ARIMAモデル、ARIMAXモデル

テキストの紹介、引用表記、シリーズまえがきは、このリンクの記事をご参照ください。

テキストで使用するデータは、R・Stan等のサンプルスクリプトで指定されています。
サンプルスクリプトは著者GitHubサイトからダウンロードして取得できます。

第２章 時系列分析の基本操作

インポート

この章で用いるライブラリをインポートします。

### インポート

# 基本
import numpy as np
import pandas as pd

# 日付
from datetime import time, date, datetime
from dateutil import tz

# Rデータセット・一般化線形モデル・時系列分析
import statsmodels.api as sm
from statsmodels.tsa.seasonal import seasonal_decompose, STL
from statsmodels.graphics.tsaplots import plot_acf

# Googleトレンドアクセス
from pytrends.request import TrendReq

# ARIMAモデル自動選択
import pmdarima as pm

# グラフ描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'

# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')

【補足】パッケージのインストール
利用環境に応じてパッケージをインストールしてください。
以下はインストールの参考コードです。

### インストール

## pytrends
# anaconda
conda install -c conda-forge pytrends
# pip
pip install pytrends

## pmdarima
# anaconda
conda install -c conda-forge pmdarima
# pip
pip install pmdarima

2.4.5 自己相関

① ホワイトノイズの自己相関
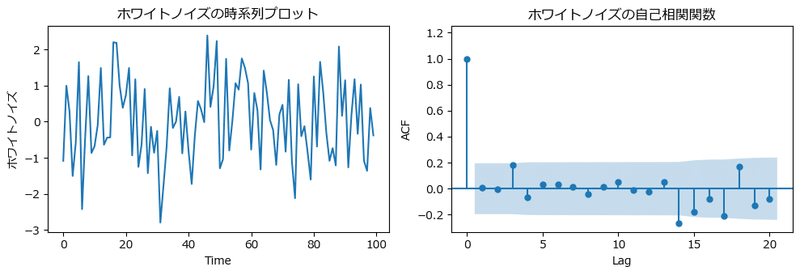
ホワイトノイズの自己相関関数を描画します。

自己相関関数の算出と描画にはstatsmodelsのplot_acfを利用しています。
テキストの図2.15に相当します。

### ホワイトノイズの自己相関 ※図2.15に相当

## データの作成
# 初期値設定
np.random.seed(123)
# White noiseの作成
white_noise = np.random.randn(100)

## 描画
fig, ax = plt.subplots(1, 2, figsize=(10, 3.5))
# ホワイトノイズの描画
ax[0].plot(white_noise)
# 自己相関関数の描画
plot_acf(white_noise, lags=20, ax=ax[1], auto_ylims=True,
         title='ホワイトノイズの自己相関関数')
# 修飾
ax[0].set_title('ホワイトノイズの時系列プロット')
ax[0].set_xlabel('Time')
ax[0].set_ylabel('ホワイトノイズ')
ax[1].set_xlabel('Lag')
ax[1].set_ylabel('ACF')
plt.tight_layout()
plt.show()

【実行結果】
自己相関関数のグラフの青い領域は95%信用区間です。
ラグ０を除き、ほぼ自己相関関数は95%信用区間内に収まっています。
なお、テキストの乱数生成と一致しないため、グラフも一致しません。

② ランダムウォーク
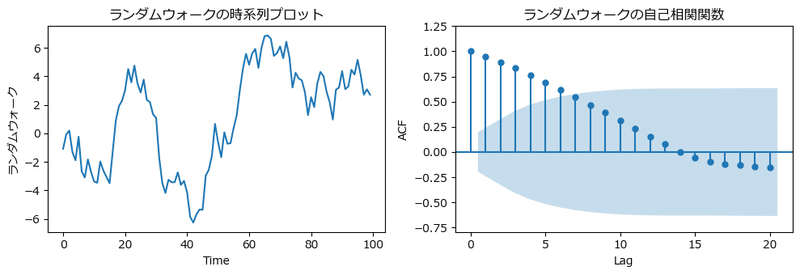
ランダムウォークの自己相関を描画します。
テキストの図2.16に相当します。

### ランダムウォークの描画 ※図2.16に相当

## データの作成
# 初期値設定
np.random.seed(123)
# ランダムウォークの作成
random_walk = np.cumsum(np.random.randn(100))

## 描画
fig, ax = plt.subplots(1, 2, figsize=(10, 3.5))
# ホワイトノイズの描画
ax[0].plot(random_walk)
# 自己相関関数の描画
plot_acf(random_walk, lags=20, ax=ax[1], auto_ylims=True,
         title='ランダムウォークの自己相関関数')
# 修飾
ax[0].set(title='ランダムウォークの時系列プロット', xlabel='Time',
          ylabel='ランダムウォーク')
ax[1].set(xlabel='Lag', ylabel='ACF')
plt.tight_layout()
plt.show()

【実行結果】
自己相関関数は滑らかな減衰を示しています。
ラグ５あたりまで有意な自己相関が見られます。
なお、テキストの乱数生成と一致しないため、グラフも一致しません。

③ 季節成分の含まれたデータ
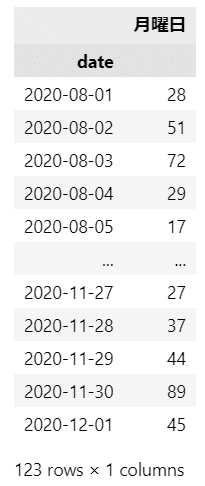
「月曜日」を含むGoogle検索データを取得して、７日の周期性の様子を確認します。
pytrendsライブラリを利用してGoogleトレンドに接続し、検索回数データを取得します。

### 季節成分の含まれたデータの描画
# https://norari-kurari-way.com/python-trend/

## Googleトレンドから検索キーワードの検索数を取得
# Googleトレンド接続用の設定
pytrends = TrendReq(hl='ja-JP', tz=540)    # 接続設定
# 検索キーワードのリストに設定
keywords = ['月曜日']
# Googleトレンドに接続
pytrends.build_payload(keywords, timeframe='2020-08-01 2020-12-01', geo='JP')
# 検索回数を取得
trend = pytrends.interest_over_time().drop('isPartial', axis=1)

# 取得データの表示
display(trend)

【実行結果】
検索ワード「月曜日」の日別検索回数を取得しました。

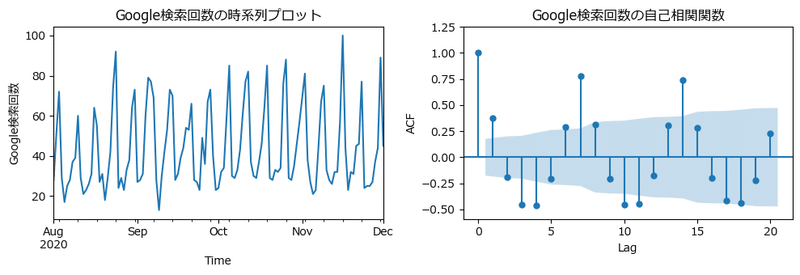
検索回数データを描画します。

## 描画 ※図2.17に相当
fig, ax = plt.subplots(1, 2, figsize=(10, 3.5))
# 検索数の描画
trend.plot(ax=ax[0], legend=False)
# 自己相関関数の描画
plot_acf(trend, lags=20, ax=ax[1], auto_ylims=True,
         title='Google検索回数の自己相関関数')
# 修飾
ax[0].set(title='Google検索回数の時系列プロット', xlabel='Time',
          ylabel='Google検索回数')
ax[1].set(xlabel='Lag', ylabel='ACF')
plt.tight_layout()
plt.show()

【実行結果】
７日、１４日に自己相関が見られます。
７日の周期性があることが分かります。

2.5 時系列の分解

① 移動平均法による分解
statsmodelsのseasonal_decomposeを用いて、トレンド成分、7日周期の季節成分、不規則変動成分に分離します。
テキストの図2.18に相当します。

### 移動平均法による時系列の分解 ※図2.18に相当

## 変動成分の分解
trend_decomp = seasonal_decompose(trend, model='additive', period=7,
                                  two_sided=True)
## 描画
fig, ax = plt.subplots(4, 1, figsize=(8, 8), sharex=True)
trend_decomp.observed.plot(ax=ax[0])
ax[0].set_ylabel('原系列')
trend_decomp.trend.plot(ax=ax[1])
ax[1].set_ylabel('トレンド変動')
trend_decomp.seasonal.plot(ax=ax[2])
ax[2].set_ylabel('季節変動')
trend_decomp.resid.plot(ax=ax[3])
ax[3].set_ylabel('不規則変動')
plt.suptitle('Google検索回数－検索ワード「月曜日」')
plt.tight_layout();

【実行結果】
季節変動はきれいな周期性を見せてくれました。

② LOESSによる分解
statsmodelsのSTLを用いて、トレンド成分、7日周期の季節成分、不規則変動成分に分離します。
テキストの図2.18左側に相当します。

### LOESSによる時系列の分解 ※図2.19左に相当

## 変動成分の分解
trend_stl = STL(trend['月曜日'], period=7).fit()

## 描画
fig, ax = plt.subplots(4, 1, figsize=(8, 8), sharex=True)
trend_stl.observed.plot(ax=ax[0])
ax[0].set_ylabel('原系列')
trend_stl.seasonal.plot(ax=ax[1])
ax[1].set_ylabel('季節変動')
trend_stl.trend.plot(ax=ax[2])
ax[2].set_ylabel('トレンド変動')
trend_stl.resid.plot(ax=ax[3])
ax[3].set_ylabel('不規則変動')
plt.suptitle('Google検索回数－検索ワード「月曜日」')
plt.tight_layout();

【実行結果】
トレンド成分がテキストよりも滑らかな曲線になりました。

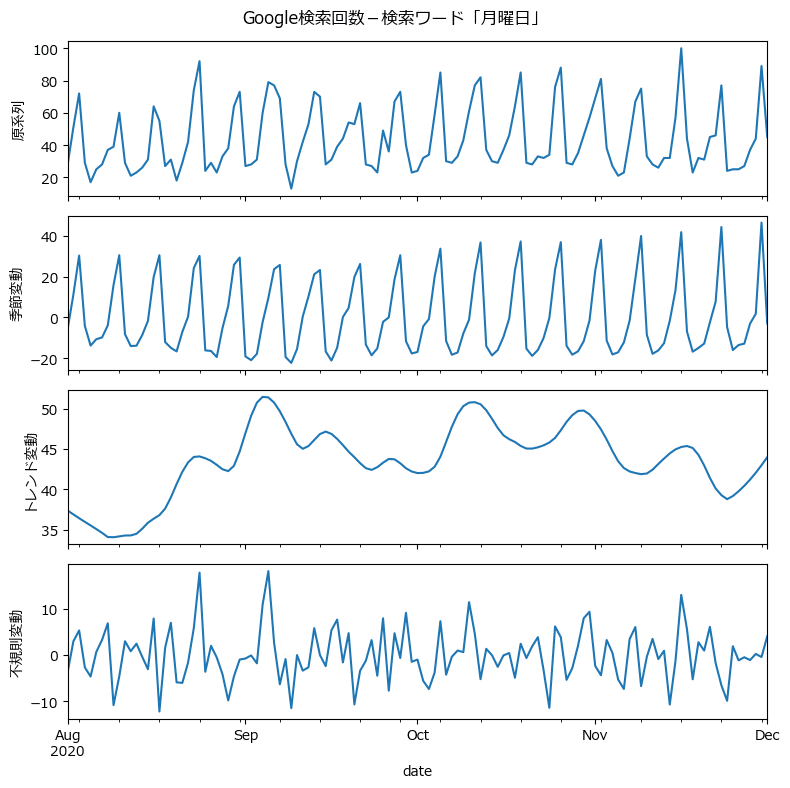
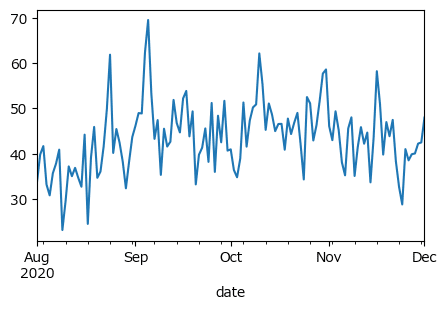
トレンド成分と不規則変動成分を足して（つまり季節変動成分を除いて）、描画します。
テキストの図2.18右側に相当します。

# 季節調整後のデータの描画 ※図2.19右に相当
ex_season = trend_stl.trend + trend_stl.resid
ex_season.plot(figsize=(5, 3));

【実行結果】
テキストと若干異なります。

2.6.1 ARモデル

① AR(1)モデル
自己回帰係数$${\phi=0.1,\ 0.9}$$の自己回帰モデルAR(1)過程を描画します。
テキストの図2.20に相当します。

### ARモデル ※図2.20に相当

## AR(1)過程の乱数生成関数の定義
# 引数 phi:自己回帰係数φ、num:乱数の個数、sigma:誤差の標準偏差、seed：乱数シード
def ar1_sim(phi, num, sigma=1, seed=123):
    np.random.seed(seed) 
    ar1_rand = np.zeros(num)
    for i in range(1, num):
        ar1_rand[i] = phi * ar1_rand[i-1] \
                      + np.random.normal(loc=0, scale=sigma, size=1)
    return ar1_rand

## AR(1)モデルの乱数取得
# AR(1)モデル (φ=0.1)
ar1_small = ar1_sim(phi=0.1, sigma=0.1, num=500)
# AR(1)モデル (φ=0.9)
ar1_large = ar1_sim(phi=0.9, sigma=0.1, num=500)

## 描画
fig, ax = plt.subplots(2, 2, figsize=(10, 6))
# AR(1), φ=0.1の描画
ax[0, 0].plot(ar1_small, lw=0.7)
plot_acf(ar1_small, lags=20, ax=ax[1, 0], title=None, auto_ylims=True,)
# AR(1), φ=0.9の描画
ax[0, 1].plot(ar1_large, lw=0.7)
plot_acf(ar1_large, lags=20, ax=ax[1, 1], title=None, auto_ylims=True)
# 修飾
ax[0, 0].set(title=r'$\phi$=0.1', xlabel='Time', ylabel='$y_1$')
ax[0, 1].set(title=r'$\phi$=0.9', xlabel='Time', ylabel='$y_1$')
ax[1, 0].set(xlabel='Lag', ylabel='ACF')
ax[1, 1].set(xlabel='Lag', ylabel='ACF')
plt.tight_layout()
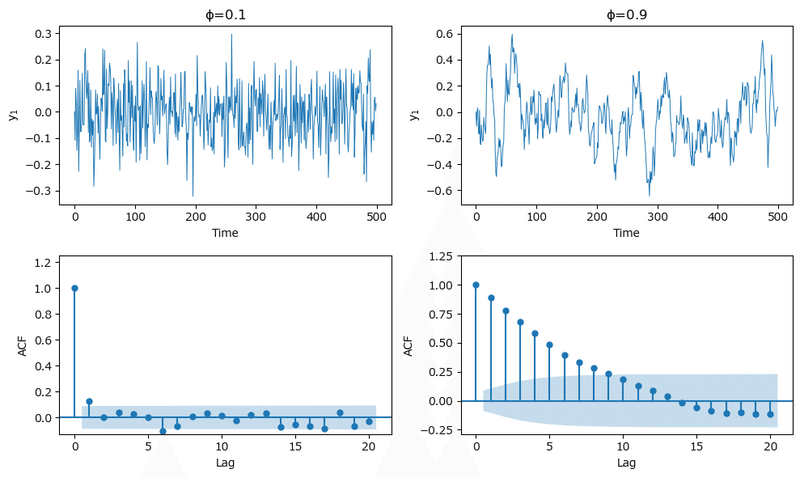
plt.show()

【実行結果】
$${\phi=0.9}$$にはラグ８くらいまで自己相関が見られます。

2.6.3 ARMA, ARIMA, ARIMAXモデル

① ARIMAモデル
Rデータセットからナイル川データを取得して、ARIMAモデルに当てはめます。
pmdarimaのauto_arimaを用いて自動モデル選択を実行します。

まずはデータ取得から。

### ARIMAモデル

# Nileデータセットの読み込み
data_nile = sm.datasets.get_rdataset('Nile', 'datasets')
nile_df = data_nile.data.set_index('time')

# 描画
fig, ax = plt.subplots(2, 1, figsize=(8, 6))
# Nileデータセットのグラフ描画
nile_df.plot(title=data_nile.title, ax=ax[0], legend=False);
# おまけ：Nileデータセットの自己相関関数の描画
plot_acf(nile_df, lags=20, ax=ax[1], auto_ylims=True)
# 修飾
ax[1].set(xlabel='Lag', ylabel='ACF')
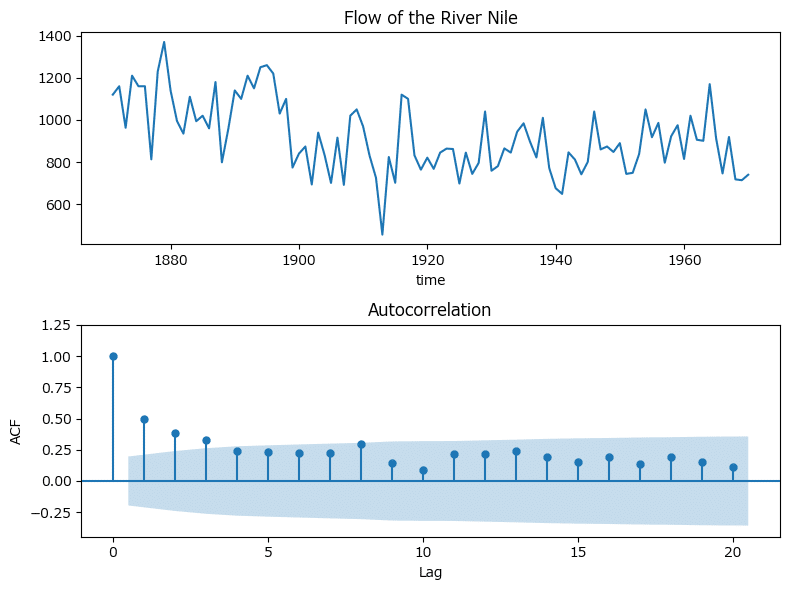
plt.tight_layout();

【実行結果】
ラグ１の自己相関が有意です。

続いて、auto_arimaのモデル選択です。
コードは１行です。

# モデル選択　ベストモデルはARIMA(1, 1, 1)
arima_model = pm.auto_arima(nile_df, trace=True)

【実行結果】
AICによるベストモデルは「ARIMA(1,1,1)」です。

ベストモデルの分析結果を確認しましょう。
auto_arimaの実行結果を代入した変数arima_modelに対して、summary()を実行します。

# 分析結果
print(arima_model.summary())

【実行結果】
ar.L1、ma.L1, sigma2は、テキストのsummary()で見られるAR係数、MA係数、sigma^2の値と若干相違します。

20期先までの予測をしましょう。
テキストの図2.21に相当します。

まずは予測値の算出から。
arima_modelに対して「predict」を実行することで、予測できます。
引数n_periodsで予測期間、return_conf_int=Trueで信頼区間の取得あり、alphaで1-信頼区間を指定します。

# 予測と信頼区間のプロット

# 予測、95%信用区間の取得
pred, conf_int95 = arima_model.predict(n_periods=20, return_conf_int=True,
                                       alpha=0.05)
# 50%信頼区間の取得
_, conf_int50 = arima_model.predict(n_periods=20, return_conf_int=True,
                                    alpha=0.5)

続いて描画です。
matplotlibで実直にプロットします。

# 描画 ※図2.11に相当

plt.figure(figsize=(8, 4))
# Nileデータセットの描画
plt.plot(nile_df);
# 予測値の描画
plt.plot(pred.index + nile_df.index[0], pred, color='red')
# Nileデータセットと予測値のつなぎ目の描画
plt.plot([nile_df.index[-1], nile_df.index[-1]+1],
         [nile_df.iloc[-1, 0], pred.iloc[0]], color='red')
# 予測値の95%信頼区間の描画
plt.fill_between(pred.index + nile_df.index[0], conf_int95[:, 0], conf_int95[:, 1],
                 color='tomato', alpha=0.2)
# 予測値の50%信頼区間の描画
plt.fill_between(pred.index + nile_df.index[0], conf_int50[:, 0], conf_int50[:, 1],
                 color='tomato', alpha=0.5)
# 修飾
plt.title('ARIMA(1,1,1)モデルの予測')
plt.xlabel('Time');

【実行結果】
赤い部分が予測値です。800強という感じでしょう。

② ARIMAXモデル
ダムの有無（0:なし、1:あり）の二値を持つ外生変数 x を用いたARIMAXモデルを検討します。
auto_arimaの引数 X に外生変数 x を指定します。

### ARIMAXモデル

# 外生変数（ダムのない1902年までの31年間：0、ダム完成後の69年間：1）
x = np.array([0] * 31 + [1] * 69).reshape(-1, 1)

# モデル選択　ベストモデルはARIMA(1,0,0)
arimax_model = pm.auto_arima(nile_df, X=x, trace=True)

【実行結果】
AICによるベストモデルは「ARIMA(1,0,0)」です。
和分・MAの次数が０になりました。

分析結果を確認します。

# 分析結果
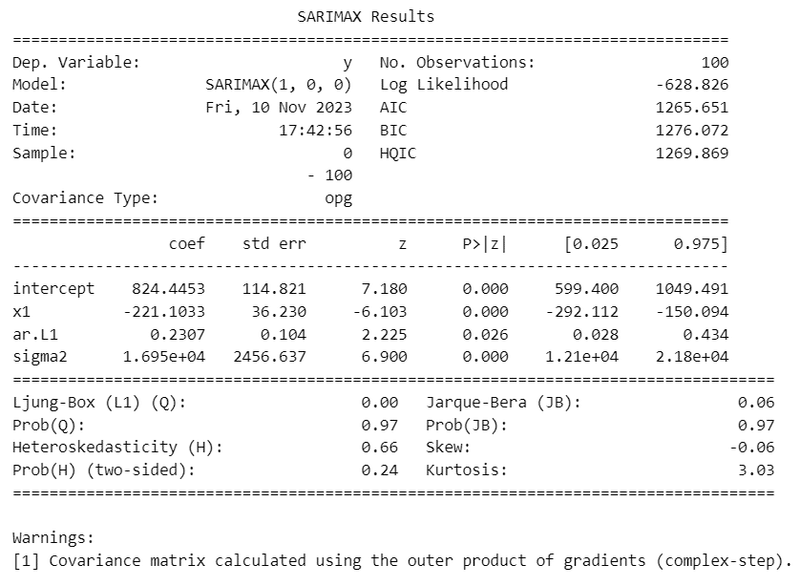
print(arimax_model.summary())

【実行結果】
x1の係数は$${-221.1}$$。
ダムの完成によって流量が$${221.1}$$減少したことを示しています。

このモデルで予測をします。
テキストにならって、予測期間にはダムが無いという条件、x=0 とします。

# ダムが取り壊された場合の将来予測

# 将来の20年間、ダムが無い＝ダムが取り壊されたとする変数xを作成
x_pred = np.zeros(20).reshape(-1, 1)

# 予測、95%信用区間の取得
y_pred, conf_int95 = arimax_model.predict(n_periods=20, X=x_pred, 
                                          return_conf_int=True,alpha=0.05)
# 50%信頼区間の取得
_, conf_int50 = arimax_model.predict(n_periods=20, X=x_pred,
                                     return_conf_int=True, alpha=0.5)

# 描画 ※図2.22に相当

plt.figure(figsize=(8, 4))
# Nileデータセットの描画
plt.plot(nile_df)
# 予測値の描画
plt.plot(y_pred.index + nile_df.index[0], y_pred, color='red')
# Nileデータセットと予測値のつなぎ目の描画
plt.plot([nile_df.index[-1], nile_df.index[-1]+1],
         [nile_df.iloc[-1, 0], y_pred.iloc[0]], color='red')
# 予測値の95%信頼区間の描画
plt.fill_between(y_pred.index + nile_df.index[0],
                 conf_int95[:, 0], conf_int95[:, 1], color='tomato', alpha=0.2)
# 予測値の50%信頼区間の描画
plt.fill_between(y_pred.index + nile_df.index[0],
                 conf_int50[:, 0], conf_int50[:, 1],
                 color='tomato', alpha=0.5)
# 修飾
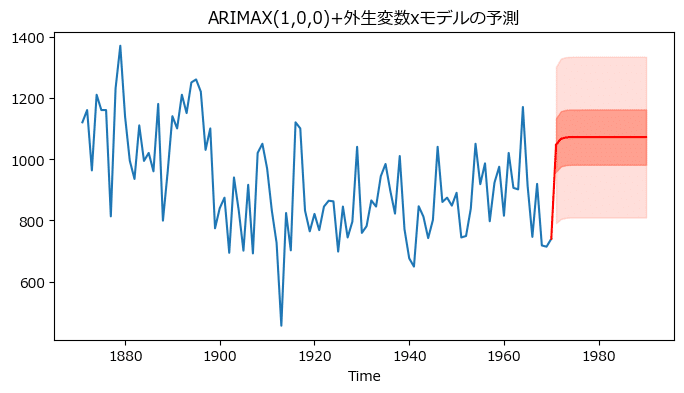
plt.title('ARIMAX(1,0,0)+外生変数xモデルの予測')
plt.xlabel('Time');

【実行結果】
赤い予測流量が増えました！およそ1100です。

第３章 へ続く

■次回の取り組みテーマ
時系列回帰分析に関する次の基本的な事項
・単位根過程、単位根検定、系列相関、ダービン-ワトソン比、一般化最小二乗法、対数変換、季節調整

次の記事

前の記事

目次

ブログの紹介

note で４つのシリーズ記事を書いています。
ぜひ覗いていってくださいね！

１．のんびり統計
統計検定２級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定２級公式問題集CBT対応版に対応しています。

２．実験！たのしいベイズモデリングをPyMC Ver.5で

書籍「たのしいベイズモデリング」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは Ｒ言語＋Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう！

３．Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learn と PyTorch の教科書です。
よかったらぜひ、お試しくださいませ。

４．データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Python のコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。

最後までお読みいただきまして、ありがとうございました。