はじめに

シリーズ数学とPythonのご案内

「シリーズ数学とPython」は、数学の学習中に「解けない、無理～」と焦ったときに、Pythonで数値の動きや可視化を行って、理解の糸口を見つけたときのことを記事にします。

データサイエンス数学ストラテジスト上級公式問題集

この記事は「データサイエンス数学ストラテジスト上級公式問題集」の問題の解読中に見つけたヒントを取り扱います。

今回取り組む問題

問題２９「確率密度関数の係数の値を求めよう！」

Python実装

やりたいこと

次のことに留意して、解答で得られた確率密度関数を可視化します。

• 確率変数$${x}$$の値に応じて関数の式を「場合分け」します。

• sympyで定義した関数になるべく手加工を加えること無く、グラフ描画ツールに連携します。

作戦

SymPy をベースにして実装します。
SymPyはPythonの代数計算ライブラリです。
描画には ①sympy、②spb : sympy plotting backends、③matplotlib の３つを試します。

実装の開始

インポート
spb : sympy plotting backends は sympy の描画をサポートするライブラリです。
必要に応じて、インストールします。
以下はcondaコマンドによるインストールコード例です。

conda install -c conda-forge sympy_plot_backends

インポートです。

import sympy
import spb
import numpy as np
import matplotlib.pyplot as plt

場合分けの式の設定
次の確率密度関数の「場合分けの式」を sympy で定義します。

$$
f(x)=
\begin{cases}
6(x-x^2) & (0 \leq x \leq 1) \\
0 & (x<0,\ 1<x)
\end{cases}
$$

sympy の Piecewise の中に複数の「関数と条件」を書くことで、場合分けを表現できます。
引数は、Piecewise( ( 関数1, 条件1 ), ( 関数2, 条件2 ), ･･･ ) です。

# 計算結果の数式を見やすくする
sympy.init_printing

# 変数xの定義
sympy.var('x')

# 場合分けの式の定義
f_piecewise = sympy.Piecewise((0, x<0),(0, x>1), (6*(x-x**2), True))
f_piecewise

# なお、次の式ではうまくプロットできなかった
# f_piecewise = sympy.Piecewise((6*(x-x**2), x>=0), (6*(x-x**2), x<=1), (0, True))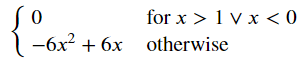

全事象$${\Omega}$$の確率$${P(\Omega)}$$は$${1}$$です。
この式を積分して結果が１になることを確認します。
sympy の integrate で関数、（変数、区間下端、区間上端）を指定します。
sympy.oo で無限大を表現しています。

# 定積分
sympy.integrate(f_piecewise, (x, -sympy.oo, sympy.oo))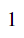

１になりました。ＯＫです！

続いて、３つのライブラリで描画します。
なるべくシンプルなコード（修飾などをしない）で書きます。
すべてのグラフは$${-0.5 \leq x \leq 1.5}$$の範囲を描画しています。

グラフの描画① sympy の plot

まずは、sympy の plot で描画します。

# f(x)のプロット sympy.plotの利用
sympy.plot((f_piecewise, (x, -0.5, 1.5)));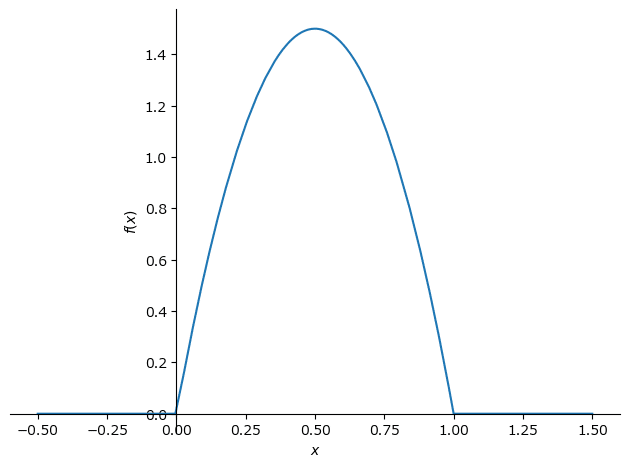

グラフの描画② spb : sympy plotting backends の plot

続いて、sympy plotting backends でプロットします。

# f(x)のプロット sympy plotting backendsの利用
spb.plot_piecewise(f_piecewise, (x, -0.5, 1.5), dots=False);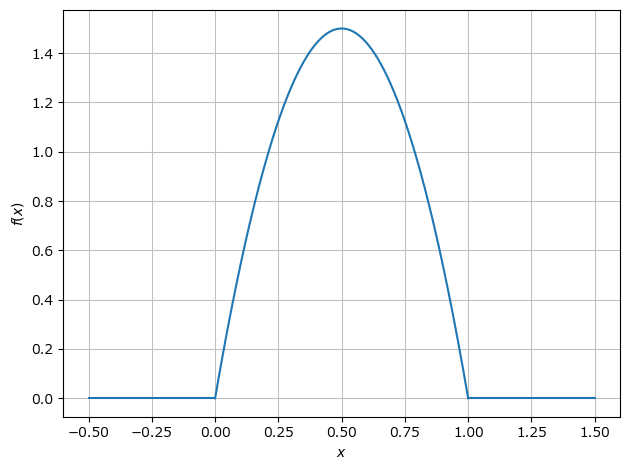

グラフの描画③ matplotlib

sympy の lambdify を利用して、sympy で定義した関数 f_piecewise  をnumpyで利用可能なオブジェクトに変換して、y1 に代入します。

# f(x)のプロット matplotlibの利用

# sympyの関数の定義をnumpyのufuncに変換
y1 = sympy.lambdify(x, f_piecewise, 'numpy')

# xの値の設定
x1 = np.linspace(-0.5, 1.5, 1001)

# プロット
plt.plot(x1, y1(x1));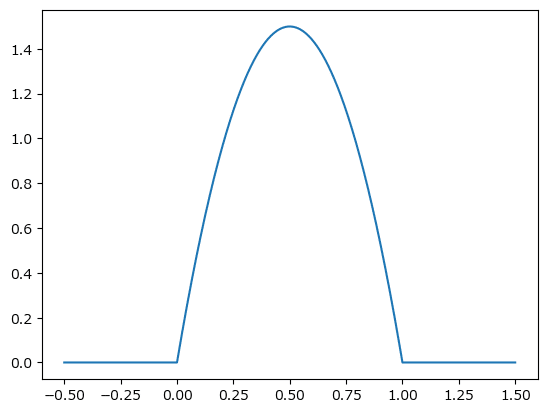

出っ張った部分の面積が１になります。
お好みのグラフは見つかりましたか？

今回も可視化できてよかったです！
（数式と比べて優しい温もりを感じます😉）

おまけ
Pythonで問題集の問題を解くコードです。
Jupyter Notebook のセル（計算ステップ）ごとに、計算結果を表示しています。

### インポート
import sympy

### 変数定義、関数定義 

# 計算結果の数式を見やすくする
sympy.init_printing

# 変数aの定義
a = sympy.Symbol('a')

# 変数xの定義
x = sympy.Symbol('x')

# f(x) (0≦x≦1)の定義
f = a*(x-x**2)
f

# f(x)の定積分計算　積分区間[0, 1]

f_int = sympy.integrate(f, (x, 0, 1))
f_int

# 定数aの解　★解答１

a_solv = sympy.solve(f_int - 1)[0]
a_solv

# f(x) (0≦x≦1)の再定義（定数aにaの解を代入）

f_pdf = f.subs(a, a_solv)
f_pdf

# xの期待値の計算：E[x] = ∫ x f(x) dx

E_x = sympy.integrate(x * f_pdf, (x, 0, 1))
E_x

# x^2の期待値の計算：E[x^2] = ∫ x^2 f(x) dx

E_x2 = sympy.integrate(x**2 * f_pdf, (x, 0, 1))
E_x2

# xの分散の計算：V[x] = E[x^2] - (E[x])^2　★解答２

V_x = E_x2 - E_x **2
V_x

おわりに

またまた SymPy で問題集の計算から道草しました。
飽きないおもちゃを見つけたみたいです🪁

おわり

ブログの紹介

noteで３つのシリーズ記事を書いています。
ぜひ覗いていってくださいね！

１．のんびり統計
統計検定２級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定２級公式問題集CBT対応版に対応しています。

２．Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。

３．データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。