今回の統計トピック

カテゴリ６の標本分布の分野に進みます。
今回は正規分布近似を応用した母比率の信頼区間の導出です。
標本比率$${\hat{p}}$$（pハット）を用いて母比率$${p}$$の区間推定に取り組みます！

公式問題集の準備

「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください！
「知る」「実践する」の章で、のんびり統計をお楽しみください！

問題を解く

📘公式問題集のカテゴリ

標本分布の分野
問1 標本割合$${\hat{p}}$$の標本分布（データなし）

試験実施年月
調査中

問題

公式問題集をご参照ください。

解き方

題意
標本サイズ$${n}$$が十分大きい場合の標本比率$${\hat{p}}$$について、信頼区間を導く過程を計算式で追いかける問題です。
問題文章に沿って素直に数式を組み立てることで解答を得られます。
問題を要約します。

小噺を少々。

標本比率$${\boldsymbol{\hat{p}}}$$ 
母集団から単純無作為抽出などの方法で抽出した標本（サンプル）より得た比率が標本比率$${\hat{p}}$$です。
内閣支持率、選挙の出口調査の得票率、テレビの視聴率などなど、さまざまなシーンで「標本比率」が活躍しています。

標本比率$${\hat{p}}$$は確率変数です。
標本比率$${\hat{p}}$$によって母集団の本当の比率＝母比率$${p}$$を推定します。

標本比率と正規分布
標本の大きさ（調査した数）を$${n}$$個とします。
標本比率などの「母集団から抽出した標本から得た推定量」が従う分布を標本分布と呼びます。
$${\boldsymbol{n}}$$の数が大きい場合、標本比率$${\boldsymbol{\hat{p}}}$$は正規分布に近似的に従います。
そこで「標準正規分布」を利用して母集団の「母比率を統計的に推定」します。

標準正規分布
平均$${\mu}$$、分散$${\sigma^2}$$の正規分布$${N(\mu,\ \sigma^2)}$$に従う確率変数$${X}$$について、次の標準化を施すと、平均$${0}$$、分散$${1}$$の標準正規分布$${N(0,\ 1)}$$に従う確率変数$${z}$$に変身しまーす、ゼーッド！。

$${z=\cfrac{X-\mu}{\sqrt{\sigma^2}}=\cfrac{確率変数X-平均}{\sqrt{分散}}}$$

支持率$${p}$$も標準化して$${z}$$にします。

区間推定
「支持率は概ね40%～45%」のように一定の区間幅をもって推定する方法を区間推定と呼びます。
信頼係数に 95% を用いるとき、「支持率（の母比率）の95%信頼区間は40%～45%」のような表現をします。

信頼区間と標準正規分布
標準化した支持率$${z}$$をイメージしましょう。
さらに支持率$${z}$$の信頼係数が 95% のときの標準正規分布を想起します。
確率 95% に相当する青い領域、下側確率 2.5%・上側確率 2.5% に相当する赤い領域をイメージしつつ、$${z}$$値 である$${-1.96}$$、$${1.96}$$を得ます。
ゼッドをゲット！

問題文章の$${-1.96}$$、$${1.96}$$は、標準正規分布の確率 95% の区間なのです。
$${1.96}$$は統計界のマジックナンバーなのです！

問題に戻ります。
数式が並びます。何卒、何卒。

標準正規分布に従う確率変数$${\boldsymbol{z}}$$
標準化の式$${z=\cfrac{X-\mu}{\sqrt{\sigma^2}}}$$に、確率変数$${X=\hat{p}}$$、平均$${\mu=p}$$、標準偏差$${\sigma=\sqrt{\cfrac{p(1-p)}{n}}}$$を代入します。

$$
z=\cfrac{X-\mu}{\sqrt{\sigma^2}}=\cfrac{\hat{p}-p}{\sqrt{\cfrac{p(1-p)}{n}}}
$$

（ア）の解答選択肢は（$${z=}$$）$${\cfrac{\hat{p}-p}{\sqrt{{p(1-p)/n}}}}$$です。

$${\boldsymbol{p}}$$の95%信頼区間
問題文に沿って式を変形します。

$$
-1.96 \leq Z \leq 1.96 \\
  \\
-1.96 \leq \frac{\hat{p}-p}{\sqrt{{p(1-p)/n}}} \leq 1.96 \\
  \\
-1.96 \sqrt{p(1-p)/n} \leq \hat{p}-p \leq 1.96 \sqrt{p(1-p)/n} \\
  \\
-\hat{p}-1.96 \sqrt{p(1-p)/n} \leq \ -p \ \leq -\hat{p}+1.96 \sqrt{p(1-p)/n}\\
  \\
\hat{p}+1.96 \sqrt{p(1-p)/n} \geq \ p \ \geq \hat{p}-1.96 \sqrt{p(1-p)/n}\\
  \\
\hat{p}-1.96 \sqrt{p(1-p)/n} \leq \ p \ \leq \hat{p}+1.96 \sqrt{p(1-p)/n}\\
$$

$${\hat{p}-1.96 \sqrt{p(1-p)/n} \leq \ p \ \leq \hat{p}+1.96 \sqrt{p(1-p)/n}}$$です。
（イ）の解答選択肢は$${1.96 \sqrt{p(1-p)/n}}$$です。

解答

③ （ア） $${\cfrac{\hat{p}-p}{\sqrt{{p(1-p)/n}}}}$$、（イ）$${1.96 \sqrt{p(1-p)/n}}$$ です。

難易度　やさしい

・知識：母比率の区間推定
・計算力：数式組み立て（中）、数式計算（低）
・時間目安：1分

知る

おしながき

公式問題集の問題に接近してみましょう！
今回は、記事「5-4 ２項分布の正規近似」とリンクして母比率の区間推定にトライしていきましょう！

母比率の推定

📕公式テキスト：3.3.4 母比率の推定（118ページ～）
記事「5-4 ２項分布の正規近似」の類題にアレンジを加えて、母比率の区間推定に迫ります。
公式テキストにならって、二項分布、標本比率、標準化、区間推定の順で書きます。
有限母集団修正は省略いたします。

類題

無作為抽出した100人に選挙の出口調査を行ったところ、X候補者に投票した人$${x}$$は 52人であり、得票率（標本比率）$${\hat{p}}$$は 0.52 でした。
母集団のX候補者の得票率（母比率）を$${p}$$とし、標本比率$${\hat{p}}$$を確率変数とするとき、得票率$${p}$$の 95% 信頼区間を求めます。
なお、$${n=100}$$は大きいものとして取り扱います。

二項分布

二項分布は成功確率$${p}$$のベルヌーイ試行を$${n}$$回の行うときの成功回数$${x}$$が従う確率分布です。$${Bin(n,p)}$$と表します。

類題について考えます。

母集団のX候補者の得票率（母比率）は$${p}$$です。
この母集団から$${n}$$人を抽出するとき、X候補者に投票した人数$${x}$$は二項分布$${Bin(n, p)}$$に従う、と想定できます。
二項分布$${Bin(n,p)}$$は、期待値$${E[x]=np}$$、分散$${V[x]=np(1-p)}$$です。
なお、母集団の大きさと非復元抽出の論点については考慮しないこととします。

イメージを促進する目的で、仮定形のグラフをプロットします。
母比率$${p}$$はわからないので仮定形のグラフになります。

母比率$${p}$$を$${0.52}$$、試行回数$${n}$$を$${100}$$と仮置きする場合、二項分布のグラフは次のようになります。

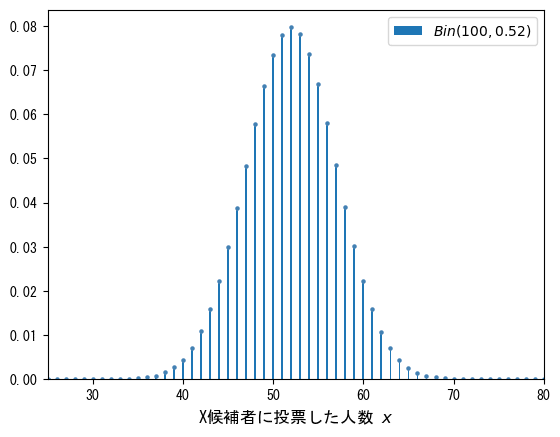
グラフの高さは確率です。
52人のときの確率 0.08 が最大です。

標本比率

標本比率は標本サイズ$${n}$$人に占めるX候補者への投票者数$${x}$$なので、$${\hat{p}=x/n}$$です。

二項分布の期待値$${E[x]=np}$$、分散$${V[x]=np(1-p)}$$を利用して、標本比率の期待値と分散を計算します。
期待値$${E[\hat{p}]}$$は$${E[x/n]=1/n \times E[x]=1/n \times np=p}$$です。
分散$${V[\hat{p}]}$$は$${V[x/n]=1/n^2 \times np(1-p)=p(1-p)/n}$$です。

また、標本サイズ$${n}$$が大きいとき、標本比率$${\hat{p}}$$は正規分布に近似的に従います。
このときの平均は$${E[\hat{p}]=p}$$、分散は$${V[\hat{p}]=p(1-p)/n}$$です。

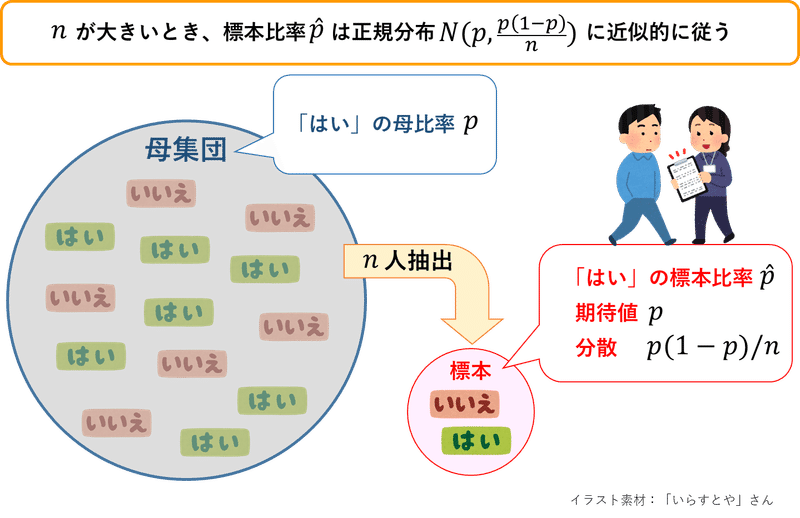
イメージを促進する目的で、仮定形のグラフをプロットします。
母比率$${p}$$はわからないので仮定形のグラフになります。

母比率$${p}$$を$${0.52}$$、試行回数$${n}$$を$${100}$$と仮置きする場合、正規分布のグラフは次のようになります。

平均$${\mu=E[p]=p=0.52}$$、分散$${\sigma^2=V[p]=p(1-p)/n=0.52\times0.48 / 100=0.002496}$$です。
二項分布のグラフに似ています。

標準化

標準化の公式$${z=\cfrac{X-\mu}{\sqrt{\sigma^2}}=\cfrac{確率変数X-平均}{\sqrt{分散}}}$$に当てはめます。

確率変数$${X}$$に標本比率$${\hat{p}}$$、平均$${\mu}$$に標本比率の期待値$${E[\hat{p}]=p}$$、分散$${\sigma^2}$$に標本比率の分散$${V[\hat{p}]=p(1-p)/n}$$を当てはめます。

得られた$${z=\cfrac{\hat{p}-p}{\sqrt{p(1-p)/n}}}$$は、標準正規分布$${N(0,1)}$$に近似的に従います。
なお、$${\boldsymbol{\sqrt{p(1-p)/n}}}$$は標準偏差です。

信頼区間に近づく～標準正規分布の確率９５％領域

標準化した確率変数$${z}$$が$${-1.96～1.96}$$の値を取るとき、標準正規分布の確率は$${P(-1.96 \leq z \leq 1.96)=0.95}$$になります。

信頼区間に迫る～母比率$${\boldsymbol{p}}$$を主役に

確率$${P(-1.96 \leq z \leq 1.96)=0.95}$$の$${z}$$に$${z=\cfrac{\hat{p}-p}{\sqrt{p(1-p)/n}}}$$を当てはめて、母比率$${p}$$について解きほぐします。

$$
確率P \left( -1.96 \leq \frac{\hat{p}-p}{\sqrt{{p(1-p)/n}}} \leq 1.96 \right)=0.95 \\
  \\
確率P(-1.96 \sqrt{p(1-p)/n\ } \leq \hat{p}-p \leq 1.96 \sqrt{p(1-p)/n}\ )=0.95 \\
  \\
確率P(-\hat{p}-1.96 \sqrt{p(1-p)/n\ } \leq \ -p \ \leq -\hat{p}+1.96 \sqrt{p(1-p)/n}\ )=0.95\\
  \\
確率P(\hat{p}+1.96 \sqrt{p(1-p)/n\ } \geq \ p \ \geq \hat{p}-1.96 \sqrt{p(1-p)/n}\ )=0.95\\
  \\
確率P(\hat{p}-1.96 \sqrt{p(1-p)/n} \leq \ p \ \leq \hat{p}+1.96 \sqrt{p(1-p)/n}\ )=0.95\\
$$

ほぐし完了です。

確率$${P(\hat{p}-1.96 \sqrt{p(1-p)/n} \leq \ p \ \leq \hat{p}+1.96 \sqrt{p(1-p)/n}\ )=0.95}$$より、

次の区間が母比率の真値$${p}$$を含む確率は 95% になります。
$${\hat{p}-1.96 \sqrt{p(1-p)/n} \leq \ p \ \leq \hat{p}+1.96 \sqrt{p(1-p)/n}}$$

こんなイメージ。

信頼区間になる～再び近似する
しかし、この区間は「正解値が分からない母比率$${p}$$」を含んでおり、計算が難しいです。
そこで、標本サイズ$${n}$$が大きいことを利用します。
大数の法則により、標本比率$${\hat{p}}$$は母比率$${p}$$に近似します。
区間の式の母比率$${p}$$を標本比率$${\hat{p}}$$に置き換えします。

$${\hat{p}-1.96 \sqrt{\hat{p}(1-\hat{p})/n} \leq \ p \ \leq \hat{p}+1.96 \sqrt{\hat{p}(1-\hat{p})/n})}$$

母比率$${\boldsymbol{p}}$$に対する95%信頼区間の公式が定まりました。
この 95% のことを信頼係数と呼びます。

これで類題の信頼区間を計算することができます！

類題の信頼区間を計算する

$${\hat{p}-1.96 \sqrt{\hat{p}(1-\hat{p})/n} \leq \ p \ \leq \hat{p}+1.96 \sqrt{\hat{p}(1-\hat{p})/n})}$$に、標本比率$${\hat{p}=0.52}$$、標本サイズ$${n=100}$$を当てはめて計算を進めましょう。

$$
\hat{p}-1.96 \sqrt{\hat{p}(1-\hat{p})/n} \leq \ p \ \leq \hat{p}+1.96 \sqrt{\hat{p}(1-\hat{p})/n)}\\
  \\
0.52-1.96\times \sqrt{0.52\times (1-0.52)/100} \leq p \leq 0.52+1.96\times \sqrt{0.52\times (1-0.52)/100} \\
 \\
0.52-1.96\times \sqrt{0.52\times 0.48 /100} \leq p \leq 0.52+1.96\times \sqrt{0.52\times 0.48/100} \\
 \\
0.52-1.96\times \sqrt{0.002496} \leq p \leq 0.52+1.96\times \sqrt{0.002496} \\
  \\
0.52-0.098 \leq p \leq 0.52+0.098 \\
  \\
0.422 \leq p \leq 0.618
$$

類題の答えが出ました！

【類題の解答】
X候補者の得票率$${p}$$の 95% 信頼区間は$${0.422 \leq p \leq 0.618}$$です。

お疲れ様でした。

母比率の信頼区間の公式の一般化

1.96 は 95% 信頼区間の場合の係数です。
信頼区間は時と場合により、90%、95%、99%などの信頼係数の値を選択します。
信頼係数を一般化しましょう。

慣例的に「$${\alpha=1-信頼係数}$$」を用います。
信頼係数 95% のとき、$${\alpha=0.05}$$です。
信頼係数 99% のとき、$${\alpha=0.01}$$です。

標準正規分布の上側確率・下側確率に注目すると、上側確率$${2.5\%}$$、下側確率$${2.5\%}$$のとき、確率は$${95\%}$$になります。
そこで、$${z}$$値に注目すると、上側$${100\alpha/2\%}$$点を$${z_{\alpha/2}}$$と表記します。

$${\pm z_{\alpha/2}}$$を用いて、母比率の信頼区間の公式を一般化します。

■よく出る信頼係数と$${z_{\alpha/2}}$$点の対応です。
信頼係数 90%：$${\alpha=0.1,\ \alpha/2=0.05}$$→$${z_{0.05}点=1.645}$$
信頼係数 95%：$${\alpha=0.05,\ \alpha/2=0.025}$$→$${z_{0.025}点=1.96}$$
信頼係数 99%：$${\alpha=0.01,\ \alpha/2=0.005}$$→$${z_{0.005}点=2.576}$$

信頼区間の意味

母比率の 95% 信頼区間とは何でしょう？

【誤り】
「母比率がこの区間に入る確率は 95% です」

【正しい】
「同じ方法で複数回の信頼区間を求めたときに、その区間に母比率を含む割合が 95% になります」
「同じ方法で 100回の区間推定を行ったときに 、95回はその区間に母比率を含みます」

少し遠回しですね。
Pythonで実験して可視化しましょう！

【実験条件】
母比率の真値$${p=0.52}$$、標本サイズ$${n=100}$$とし、正規分布$${N(0.52, \frac{0.52\times0.48}{100})}$$に従う乱数を１個取得して標本比率にします。
この標本比率から 95% 信頼区間を１個得ます。
この区間推定を 100 回繰り返します。

【結果】
横軸に実施回、縦軸に各回の信頼区間をプロットしています。
赤い水平線が母比率$${0.52}$$であり、赤い縦線が母比率を信頼区間に含まない回です。

赤い縦線は 5 回。
100 回中、95 回は母比率を信頼区間に含み、5 回は含まない、という結果がでました。
「区間推定を複数回行って母比率を信頼区間に含む回数は 95% ＝ 95% 信頼区間」ということなのです。

【誤り】の理由について深掘りしてみます。
母比率の信頼区間の公式があります。

$${\hat{p}}$$に標本から得た標本比率の値、たとえば 0.52 を入れて、95% 信頼区間の確率の式の作成を試みます。

$$
P \left(0.52-1.96 \sqrt{\cfrac{0.52 (1-0.52)}{n}} \leq \ p \ \leq \ 0.52+1.96\sqrt{\cfrac{0.052(1-0.52)}{n}} \right)
$$

母比率$${p}$$は定数なので、式の中に確率変数が含まれない状態になりました。
つまり、この式で確率を計算することができないのです！
なので「母比率がこの区間に入る確率は 95% です」は誤りなのです。

長旅、お疲れ様でした。

実践する

母比率の信頼区間を計算してみよう

標本比率、標本の大きさ、信頼係数に数字を当てはめて、母比率の信頼区間を計算しましょう！
EXCELやPythonを活用して、さくさく演算しましょう。

電卓・手作業で作成してみよう！

「知る」の類題を解いてみましょう。
また、「EXCELで作成してみよう！」の内容を参照しつつ、さまざまな標本比率、標本の大きさ、信頼係数で母比率の信頼区間を計算しましょう。
一番記憶に残る方法ですし、試験本番の電卓作業のトレーニングにもなります。

EXCELで作成してみよう！

データ数が多い場合、やはり手作業では非効率になります。
パソコンを利用して、手早く作表できるようになれば、実務活用がしやすくなるでしょう。

データシートの紹介
商品の認知度調査の体裁で母比率の信頼区間を求めるデータシートです。
青い欄の設定値を変更すると、【信頼区間】の区間下限・上限・範囲を自動計算します。
設定値を変更して信頼区間の変化をお楽しみください！

信頼区間の範囲が広すぎると、比率を絞り込むことができずにデータ活用しにくいときがありますよね！
「母比率の信頼区間の公式」をみると、信頼区間の幅に影響するパラメータが「標本の大きさ ｎ」と「信頼係数に対応するｚ値」であることが分かります。

そこで、標本の大きさと信頼係数の値を動かしてみて、信頼区間がどのように変わるのか、データシートを利用して確認しましょう！

標本の大きさを変える

標本の大きさである「調査人数」を「100人」と「10000人」で比べてみます。
信頼区間の幅が大きく変化しましたね！

標本の大きさが大きくなるにつれて、信頼区間の幅が縮まり、特定の比率にフォーカスしていきます。この例では$${0.52 \pm 0.01}$$です。
調査数を増やすことで、母比率の信頼区間の幅を縮められることが分かりました。
調査数の増加による調査コストが少ない場合には、有効な方法になるでしょう。

信頼係数を変える

信頼係数の値を小さくしました。
信頼区間の幅が若干、縮みました。

信頼係数の値を小さくすることが、調査の目的や必要とするデータの精度に合致するかどうかが、是非の鍵になりそうです。

EXCEL関数の紹介　NORM.S.INV関数
確率に対応する標準正規分布のｚ値を取得する「NORM.S.INV関数」を用いて、信頼係数に対応するｚ値を取得しています。
例えば信頼係数 95% の場合、上側確率$${0.025=(1-0.95)/2}$$のｚ値 1.96 を取得します。

EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。

Pythonで作成してみよう！

プログラムコードを読んで、データを流したりデータを変えてみたりして、データを追いかけることで、作表ロジックを把握する方法も効果的でしょう。
サンプルコードを揃えておけば、類似する作表作業を自動化して素早く結果を得ることができます。

今回は、母比率の信頼区間を計算します。
ぜひパラメータを変更して、正規分布の形状と数値の変化をご堪能ください！

①インポート
scipy.statsのnorm：正規分布、binom：二項分布、t：t分布を用いて、信頼区間を算出します。
Decimal,ROUND_HALF_UPは、四捨五入の計算に用います。

import numpy as np
from decimal import Decimal, ROUND_HALF_UP
from scipy.stats import norm, binom, t
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'MS Gothic'
%matplotlib inline

②母比率の区間推定：正規分布近似による信頼区間
「設定」の標本サイズ$${n}$$、比率$${p}$$、信頼係数$${cf}$$を設定して、正規分布近似の信頼区間を算出します。

• scipy.statsのnorm.intervalで正規分布の信頼区間を取得できます。

  • 引数は、confidence=信頼係数、loc=平均、scale=標準偏差 です。

• 二項分布の正規分布近似により、平均=$${p}$$、標準偏差=$${\sqrt{p(1-p)/n}}$$で算出しています。

# 設定 標本サイズｎ、比率ｐ、信頼係数ｃｆ
n, p, cf = 100, 0.5, 0.95

# 平均、標準偏差の計算（二項分布の正規分布近似を利用）
mu, stddev = p, (p*(1-p)/n)**(1/2)

# 信頼区間[ci_lower, ci_upper]の取得
ci_lower, ci_upper = norm.interval(confidence=cf, loc=mu, scale=stddev)

print(f'標本サイズ:{n},比率:{p}の{cf*100}%信頼区間は {ci_lower:.3f}～{ci_upper:.3f}です')


出力イメージ
標本サイズ:100,比率:0.5の95.0%信頼区間は 0.402～0.598です

③信頼係数から標準正規分布の上側確率表に相当する z 値を算出する関数
標準正規分布の上側確率表に相当するｚ値を算出します。
引数は 信頼係数$${cf}$$です。

公式問題集は「標準正規分布の上側確率表」のｚ値にもとづいて区間推定や統計的検定の計算を行っているので、作ってみました。

• norm.intervalで、平均=0、標準偏差=1にすると標準正規分布の値を得ることができます。

• 四捨五入で小数第２位に丸めます。
  正確な四捨五入をするため、Decimalを利用します（Python標準のroundは偶数丸め）。

# 信頼係数よりz値を算出する関数
def z_val_from_cf(cf):
    z_val = norm.interval(confidence=cf, loc=0, scale=1)[1]
    z_val = Decimal(str(z_val)).quantize(Decimal('0.01'), rounding=ROUND_HALF_UP) 
    return float(z_val)

# テスト出力
cfs = [0.6826, 0.9, 0.95, 0.9544, 0.99, 0.99729]
for cf in cfs:
    print(f'{cf*100:.3f}%: {z_val_from_cf(cf):.2f}')


出力イメージ
68.260%: 1.00
90.000%: 1.64
95.000%: 1.96
95.440%: 2.00
99.000%: 2.58
99.729%: 3.00

④実験：信頼区間を複数回求めて、母比率を含む区間の割合を算出する
「知る」の章の信頼区間の実験で使用したコードです。
信頼係数に対応するｚ値は③の関数で近似値（丸め値）を利用しています。

「設定」の各値を変更して、さまざまな信頼区間の実験を試行してみてくださいね！

# 設定
n, p = 100, 0.52             # 標本サイズn、母比率p
cf = 0.95                    # 信頼係数
iter_num = 100               # 区間推定を行う回数

# 初期値設定
np.random.seed(1)            # n=100, p=0.52のとき、90%:4, 95%:1, 99%:2,3
ci_z = z_val_from_cf(cf)     # 信頼係数に対応するz値 95%→1.96
mu = p                       # 母比率の平均
stddev = (p*(1-p)/n)**(1/2)  # 母比率の標準偏差
p_hat_list = []
counter = 0

# 描画領域指定
plt.figure(figsize=(10,5))

for i in range(iter_num):
    
    # 標本比率p_hatを正規分布乱数で取得、信頼区間[ci_lower, ci_upper]を算出
    p_hat = norm.rvs(mu, stddev, size=1)[0]
    ci_lower = p_hat - ci_z * (p_hat*(1-p_hat)/n)**(1/2)
    ci_upper = p_hat + ci_z * (p_hat*(1-p_hat)/n)**(1/2)
    
    # 母比率が信頼区間内：ブルー、信頼区間外：レッド
    if ci_lower <= p <= ci_upper:
        color, lw, s = 'steelblue', 0.5, 5
        counter += 1 # 母比率を信頼区間含む場合１カウント
    else:
        color, lw, s = 'red', 2.0, 10

    # プロット 実施回i+1, 信頼区間ci_lower点, ci_upper点、点を結ぶ垂直線
    plt.scatter(i+1, ci_lower, color=color, s=s)
    plt.scatter(i+1, ci_upper, color=color, s=s)
    plt.vlines(i+1, ci_lower, ci_upper, color=color, lw=lw)

    # 標本比率をリストに格納
    p_hat_list.append(p_hat)

# 修飾
plt.hlines(p, 0, iter_num+1, ec='red', lw=0.3)
plt.title(f'母比率が{cf*100:.0f}%信頼区間に含まれる割合: {counter/iter_num*100:.1f}%')
plt.xlabel('区間推定の実施回')

# plt.savefig('./ci_exp.png') # グラフ画像ファイルの保存
plt.show()

④母比率の信頼区間をさまざまな確率分布で算出
次の４つの確率分布・方法で、母比率の信頼区間を算出します。
標本サイズ$${n=100}$$の場合、４つの方法の信頼区間に大きな相違は無さそうです。

• 正規分布

  • norm.intarvalで信頼区間を算出

• 上側確率利用

  • 標準正規分布の上側確率表相当のｚ値を取得して、信頼区間を算出
    上側確率表ではｚ値が丸められています。 上記の「正規分布」と比較して、丸めの誤差の影響を確認します。

• 二項分布

  • binom.intervalで二項分布（成功回数）の信頼区間（単位は回数）を算出、標本サイズｎで割って比率化

  • 引数は、confidence=信頼係数、n=標本サイズ、p=比率

• ｔ分布

  • t.intarvalでt分布の信頼区間を算出

  • 引数は、confidence=信頼係数、df=自由度（今回は標本サイズ-1)、loc=平均、scale=標準偏差

# 設定 標準サイズｎ、母比率ｐ、信頼係数ｃｆ
n, p, cf = 100, 0.52, 0.95

# 初期値設定 乱数シード、二項分布の平均・標準偏差、標準正規分布のｚ値
np.random.seed(1)
mu, stddev = p, (p*(1-p)/n)**(1/2)
ci_z = z_val_from_cf(cf)

# ヘッダの表示
print('\n【正規分布・標準正規分布の上側確率表利用・二項分布・t分布の比較】')
print(f'母比率={p}, 標本サイズ={n}, 信頼係数={cf*100}%')
print('-'*30)

### 母比率を用いた信頼区間の比較
# サブヘッダの表示
print(f'【母比率のケース】')
print(f'標準偏差: {stddev}')
print('-'*30)
# 正規分布
lower, upper = norm.interval(confidence=cf, loc=mu, scale=stddev)
print(f'正規分布　　：{lower} ～ {upper}')
# 標準正規分布の上側確率表利用
p_ci = ci_z * stddev
print(f'上側確率利用：{p-p_ci} ～ {p+p_ci}')
# 二項分布
lower, upper = binom.interval(confidence=cf, n=n, p=p)
print(f'二項分布　　：{lower/n} ～ {upper/n}')
# t分布
lower, upper = t.interval(confidence=cf, df=n-1, loc=mu, scale=stddev)
print(f't分布 　　　：{lower} ～ {upper}')

### 標本比率を用いた信頼区間の比較
# 標本比率（正規分布乱数）、標本比率の標準偏差の算出
p_hat = norm.rvs(mu, stddev, size=1)[0]
p_hat_stddev = (p_hat*(1-p_hat)/n)**(1/2)
# サブヘッダの表示
print('\n【標本比率のケース】')
print(f'標本比率（乱数）: {p_hat}')
print(f'標準偏差: {p_hat_stddev}')
print('-'*30)
# 正規分布
lower, upper = norm.interval(confidence=cf, loc=p_hat, scale=p_hat_stddev)
print(f'正規分布　　：{lower} ～ {upper}')
# 標準正規分布の上側確率表利用
p_hat_ci = ci_z * p_hat_stddev
print(f'上側確率利用：{p_hat-p_hat_ci} ～ {p_hat+p_hat_ci}')
# 二項分布
lower, upper = binom.interval(confidence=cf, n=n, p=p_hat)
print(f'二項分布　　：{lower/n} ～ {upper/n}')
# t分布
lower, upper = t.interval(confidence=cf, df=n-1, loc=p_hat, scale=p_hat_stddev)
print(f't分布 　　　：{lower} ～ {upper}')

Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。

おわりに

「カテゴリ６：標本分布の分野」に入りました。
この分野の問題は 無味乾燥な 数式や変数がたくさん並びます。
なるべく図表を用いて直感的なイメージを心がけたいのですが、数式を展開するほうが美しかったりして、なかなか悩ましいです。

ところで、問題のカテゴリーは「標本分布の分野」なのですが、今回の問題は「推定の分野」に一歩踏み込んだ問題になっています。
標本分布から統計的推定へとつながる関係性が見えたでしょうか？

最後までお読みいただきまして、ありがとうございました。

のんびり統計シリーズの記事

次の記事

前の記事

目次