
第11章「歴代M-1グランプリで最もおもしろいのは誰か」のベイズモデリングをPyMC Ver.5 で
この記事は、テキスト「たのしいベイズモデリング」の第11章「歴代M-1グランプリで最もおもしろいのは誰か」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。
今回は初学者に優しい入門編的なモデルです。
テキストに近い推論結果を得ることもできました!
そしてなにより、M-1グランプリという話題性の高いテーマで面白く・楽しくベイズモデリングに取り組めました!
果たしてどのような切り口で「お笑いの世界」を推論するのでしょう。
PyMCでモデリングして、ベイズを楽しみましょう!
テキストの紹介、引用表記、シリーズまえがき、PyMC等のバージョン情報は、このリンクの記事をご参照ください。
テキストで使用するデータは、R・Stan等のサンプルスクリプトとともに、出版社サイトからダウンロードして取得できます。
サマリー
テキストの概要
執筆者 : 徳岡大 先生
モデル難易度: ★・・・・ (やさしい)
自己評価
評点
$$
\begin{array}{c:c:c}
実装精度 & ★★★★★& GoooD!! \\
結果再現度 & ★★★★★& 最高✨ \\
楽しさ & ★★★★★& 楽しい! \\
\end{array}
$$

評価ポイント
シンプルなモデルからはじまり、段階的にモデルを改良するアプローチを通じて、試行錯誤して構築するモデリングの醍醐味を体感できました。
推論結果で得られる「順位」が若干、テキストと異なっています。
芸人さん、先生、ごめんなさい。
でも、個人的にはそこそこ推論できていると感じたので、結果再現度を最高ランクにしました!
工夫・喜び・反省
もしも最新データを取得できたなら・・・、なんて妄想いたしました。
モデルの概要
テキストの調査・実験の概要
■13回のM-1グランプリをベイズする
テキストは、2001年から2010年までの10回と2015年から2017年までの3回のM-1グランプリの決勝に出場した62組の評価得点データ(標準化後)を用いてベイズモデリングを行い、コンビのおもしろさを推定する、と宣言しています。
コンビに対する審査員の評価得点が正規分布すると仮定して、4つのモデルをStanで構築しています。
この記事では PyMC Ver.5 で著者のモデルをなぞっていきます。

テキストの4つのモデリング
① コンビ平均モデル
コンビ$${i}$$ごとの評価得点$${Y_i}$$は、コンビごとの平均点$${\theta_i}$$と標準偏差$${\sigma_i}$$をパラメータにもつ正規分布に従うとするモデルです。
$$
Y_i \sim \text{Normal}\ (\theta_i,\ \sigma_i)
$$
② 審判員のくせ評価モデル
「審判員の評価にくせがある」との仮定を追加するモデルです。
評価得点$${Y_{ij}}$$は、コンビ$${i}$$ごとの平均点$${\theta_i}$$と審判員$${j}$$ごとの標準偏差$${\sigma_j}$$をパラメータにもつ正規分布に従うと想定されています。
$$
\begin{align*}
Y_{ij} &\sim \text{Normal}\ (\theta_i,\ \sigma_j) \\
\theta_i &\sim \text{Normal}\ (0,\ \sigma_{\theta})
\end{align*}
$$
③ 審判員の基準効果モデル
「審判員ごとに評価基準の違いがある」との仮定を追加するモデルです。
評価得点$${Y_{ij}}$$は、コンビ$${i}$$ごとの評価$${\theta_i}$$と審判員$${j}$$ごとの評価基準$${\gamma_j}$$を平均、コンビごとのバラツキ$${\sigma_i}$$を標準偏差とする正規分布に従うと想定されています。
$$
\begin{align*}
Y_{ij} &\sim \text{Normal}\ (\theta_i + \gamma_j,\ \sigma_i) \\
\theta_i &\sim \text{Normal}\ (0,\ \sigma_{\theta}) \\
\gamma_j &\sim \text{Normal}\ (0,\ \sigma_{\gamma}) \\
\end{align*}
$$
④ 開催回数効果モデル
「開催を重ねるごとに評価基準が変化する」との仮定を追加するモデルです。
評価得点$${Y_{ijo}}$$は、コンビ$${i}$$ごとの評価$${\theta_i}$$、審判員$${j}$$ごとの評価基準$${\gamma_j}$$、開催回数$${o}$$ごとの特徴$${\zeta_o}$$を平均、誤差$${\sigma_e}$$を標準偏差とする正規分布に従うと想定されています。
$$
\begin{align*}
Y_{ijo} &\sim \text{Normal}\ (\theta_i + \gamma_j + \zeta_o,\ \sigma_e) \\
\theta_i &\sim \text{Normal}\ (0,\ \sigma_{\theta}) \\
\gamma_j &\sim \text{Normal}\ (0,\ \sigma_{\gamma}) \\
\zeta_o &\sim \text{Normal}\ (0,\ \sigma_{\zeta}) \\
\end{align*}
$$
■分析・分析結果
コンビ名・審査員名を出して、EAP(事後平均)で順位付けしていますが、テキストで強調されている点「95%確信区間でみると(各コンビの間に)差があるとは言えない順位であることに留意しておく必要がある」を肝に銘じて、PyMCの実装に移ります。

PyMC実装
Let's enjoy PyMC & Python !
準備・データ確認
1.インポート
### インポート
# ユーティリティ
import pickle
# 数値・確率計算
import pandas as pd
import numpy as np
# PyMC
import pymc as pm
# import pytensor.tensor as pt
import arviz as az
# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'2.データの読み込み
csvファイルをpandasのデータフレームに読み込みます。
### データの読み込み
data = pd.read_csv('m1_score.csv')
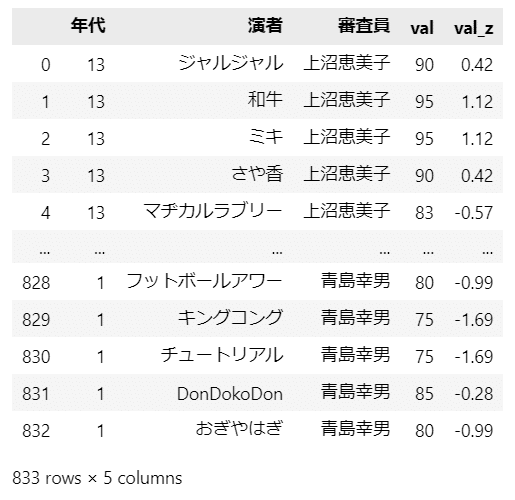
display(data)【実行結果】
全833行です。
項目は、「年代」:開催回、「演者」:お笑いコンビ名、「審査員」:審査員名、「val」:評価得点、「val_z」:標準化された評価得点、です。
3.データの外観・統計量
ひとまず要約統計量を確認します。
### 要約統計量の表示
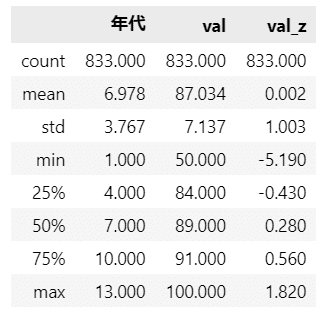
data.describe().round(3)【実行結果】
評価得点(val)は50から100まで幅広い値を取っているようです。
4.箱ひげ図の描画
seaborn の boxplot を用いて箱ひげ図を作成します。
1つ目は開催回別の評価得点です。
### 箱ひげ図のプロット1 開催回別評価得点
plt.figure(figsize=(5, 4))
sns.boxplot(data=data, x='年代', y='val', notch=True, linewidth=0.8,
color='lavender', linecolor='midnightblue')
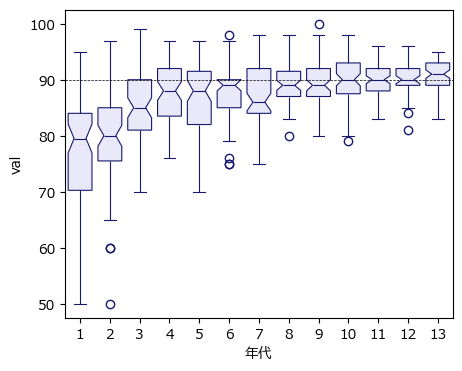
plt.axhline(90, color='black', lw=0.5, ls='--');【実行結果】
開始直後の数回はバラツキが大きかったようです。
続いてコンビ別の評価得点。
### 箱ひげ図のプロット2 コンビ別評価得点
plt.figure(figsize=(15, 4))
sns.boxplot(data=data, x='演者', y='val', notch=True, linewidth=0.8,
color='lavender', linecolor='midnightblue')
plt.axhline(90, color='black', lw=0.5, ls='--')
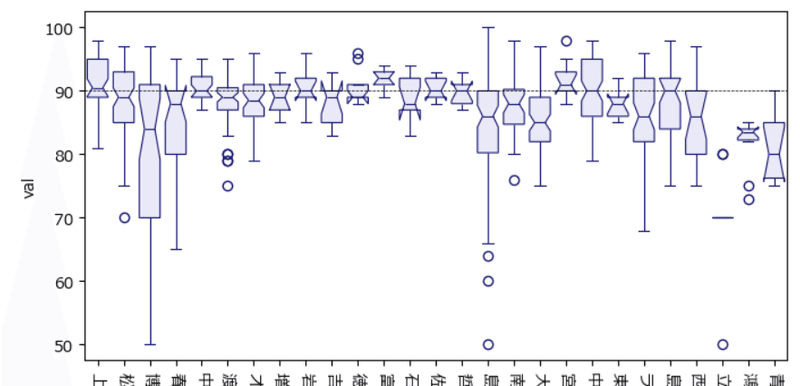
plt.xticks(rotation=270);【実行結果】
名称は一部省略いたします。
90点割れは珍しくないようですね。

最後に審査員別の評価得点。
### 箱ひげ図のプロット3 審査員別評価得点
plt.figure(figsize=(8, 4))
sns.boxplot(data=data, x='審査員', y='val', notch=True, linewidth=0.8,
color='lavender', linecolor='midnightblue')
plt.axhline(90, color='black', lw=0.5, ls='--')
plt.xticks(rotation=270);【実行結果】
名称は一部省略いたします。
審査員によってバラツキに違いがあることが分かります。
5.データの前処理
カテゴリ変数の要素とインデックスを取得します。
これらのデータはPyMCのモデル内で利用しています。
### カテゴリ変数の要素とインデックスの取得
combi_cat = pd.Categorical(data['演者']).categories
combi_idx = pd.Categorical(data['演者']).codes
judge_cat = pd.Categorical(data['審査員']).categories
judge_idx = pd.Categorical(data['審査員']).codes
times_cat = pd.Categorical(data['年代']).categories
times_idx = pd.Categorical(data['年代']).codes
モデル1:コンビ平均モデル
テキスト「11.2 コンビ平均モデル」のモデルです。
モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
添字$${i}$$はコンビのインデックスです。
また$${\theta_i}$$と$${\sigma_i}$$の事前分布はテキストに明示されていないため、十分に幅の広いパラメータを設定しました。
$$
\begin{align*}
\theta_i &\sim \text{Uniform}\ (\text{lower}=-100,\ \text{upper}=100) \\
\sigma_i &\sim \text{HalfCauchy}\ (\text{beta}=100) \\
likelihood &\sim \text{Normal}\ (\text{mu}=\theta_i,\ \text{sigma}=\sigma_i) \\
\end{align*}
$$
1.モデルの定義
### モデルの定義
with pm.Model() as model1:
### データ関連定義
# coordの定義
model1.add_coord('data', values=data.index, mutable=True)
model1.add_coord('combi', values=combi_cat, mutable=True)
# dataの定義
y = pm.ConstantData('y', value=data['val_z'].values, dims='data')
### 事前分布
# 事前分布
theta = pm.Uniform('theta', lower=-100, upper=100, dims='combi')
sigma = pm.Uniform('sigma', lower=0, upper=100, dims='combi')
### 尤度
likelihood = pm.Normal('likelihood',
mu=theta[combi_idx], sigma=sigma[combi_idx],
observed=y, dims='data')【モデル注釈】省略
2.モデルの外観の確認
### モデルの表示
model1【実行結果】
シンプルなモデルです。

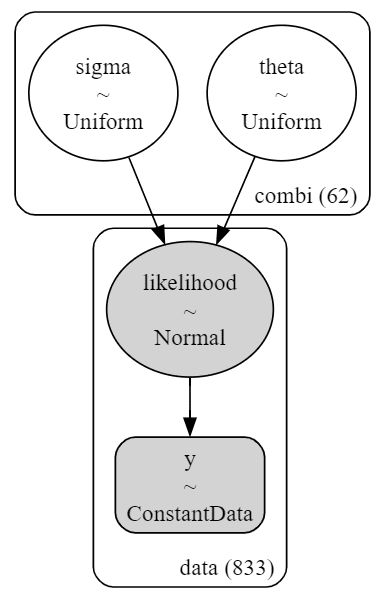
# モデルの可視化
pm.model_to_graphviz(model1)【実行結果】
シンプルなモデルです。
3.事後分布からのサンプリング
乱数生成数(draws)はテキストよりも少なめです。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ30秒でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 30秒
with model1:
idata1 = pm.sample(draws=5000, tune=5000, chains=4, target_accept=0.9,
nuts_sampler='numpyro', random_seed=123)【実行結果】省略
4.サンプリングデータの確認
$${\hat{R}}$$、トレースプロットを確認します。
事後分布の収束確認は$${\hat{R}\leq 1.1}$$としています。
### r_hat>1.1の確認
rhat_idata1 = az.rhat(idata1)
(rhat_idata1>1.1).sum()【実行結果】
$${\hat{R} >1.1}$$のパラメータは「0」件です。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。
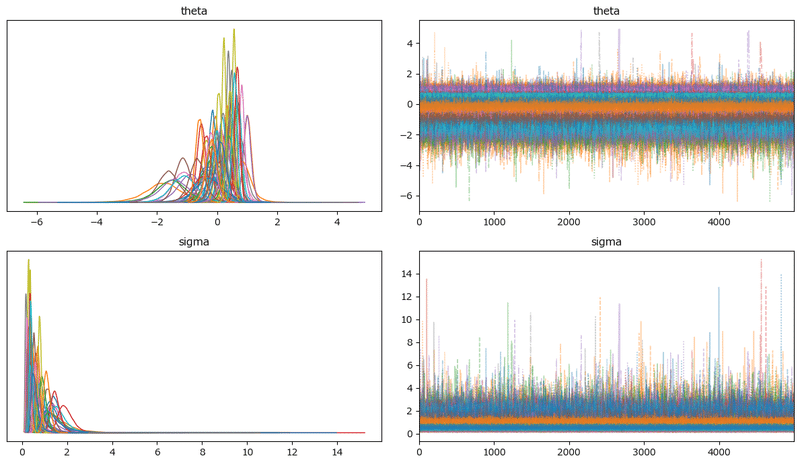
トレースプロットです。
### トレースプロットの表示
pm.plot_trace(idata1, compact=True, combined=True, figsize=(12, 7))
plt.tight_layout();【実行結果】
密集する様子は、パラメータ同士が競い合っているかのように見えます。
5.コンビ平均モデルの結果
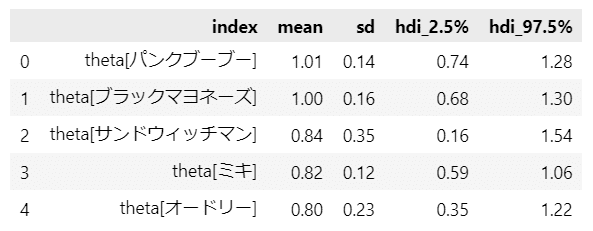
テキストの表11.1に相当する「おもしろさ($${\theta_i}$$)の事後分布の上位5組の要約統計量」を算出します。
pm.summary()関数で対応します。
### おもしろさの事後分布の上位5組の要約統計情報 ★表11.1に対応
(pm.summary(idata1, hdi_prob=0.95, kind='stats', var_names=['theta'])
.sort_values('mean', ascending=False).head(5).reset_index().round(2))【実行結果】
テキストの順番と一致しました。
平均(mean、テキストのEAP)はテキストと若干ずれがあります。
標準偏差(sd、テキストのpost.sd)はテキストと相違します。
なお、下限・上限については、テキストが信用区間(確信区間)を使用、この記事はHDIを使用しているため、相違する結果となります。
続いて、テキストの表11.2に相当する「標準偏差の事後分布の中央値・95%信用区間」を算出します。
### 標準偏差の事後分布の中央値および95%信用区間 ★表11.2に対応
# 推論データから要約統計情報を計算する関数の定義
def calc_stat(i, idata):
tmp = idata.posterior.sigma[:, :, i].data.flatten()
return [combi_cat[i], np.median(tmp), np.quantile(tmp, 0.025),
np.quantile(tmp, 0.975)]
## sigma_statsデータフレームの作成
# データフレームの初期化
sigma_stats = pd.DataFrame()
# top5の順に要約統計情報を計算してデータフレームに追加
for i in set(combi_idx):
tmp_stats = calc_stat(i, idata1)
sigma_stats = pd.concat([sigma_stats, pd.DataFrame(tmp_stats).T], axis=0)
# カラム名とインデックスの補正(型をfloatに変換の上、中央値で降順ソート)
sigma_stats.columns = ['コンビ名', '中央値', '2.5%', '97.5%']
sigma_stats = sigma_stats.astype({'中央値': float, '2.5%': float, '97.5%': float})
sigma_stats = sigma_stats.sort_values(by='中央値', ascending=False)
sigma_stats.reset_index(drop=True, inplace=True)
# 要約統計量の表示
print('【標準偏差の事後分布の中央値と95%信用区間】')
display(sigma_stats.head(3).round(2))
display(sigma_stats.tail(3).round(2))【実行結果】
テキストの順番と一致しました。
中央値、信用区間の値はテキストと若干ずれがあります。
先ほどのコンビごとの箱ひげ図で、区間幅の大きかった(つまり得点のバラツキが大きかった)コンビが上位にきています。

6.推論データ(idata)の保存
推論データを再利用する場合に備えてファイルに保存しましょう。
idata1をpickleで保存します。
### idataの保存 pickle
file = r'idata1_ch11.pkl'
with open(file, 'wb') as f:
pickle.dump(idata1, f)読み込みコードは次のとおりです。
### idataの読み込み pickle
file = r'idata1_ch11.pkl'
with open(file, 'rb') as f:
idata1_load = pickle.load(f)
モデル2:審査員のくせ評価モデル
テキスト「11.3 審査員のくせ評価モデル」のモデルです。
モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
添字$${i}$$はコンビのインデックス、$${j}$$は審査員のインデックスです。
$$
\begin{align*}
\sigma_{\theta_i} &\sim \text{HalfCaushy}\ (\text{beta}=5)\\
\theta_i &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=\sigma_{\theta_i}) \\
\sigma_j &\sim \text{HalfCauchy}\ (\text{beta}=5) \\
likelihood &\sim \text{Normal}\ (\text{mu}=\theta_i,\ \text{sigma}=\sigma_j) \\
\end{align*}
$$
1.モデルの定義
### モデルの定義
with pm.Model() as model2:
### データ関連定義
# coordの定義
model2.add_coord('data', values=data.index, mutable=True)
model2.add_coord('combi', values=combi_cat, mutable=True)
model2.add_coord('judge', values=judge_cat, mutable=True)
# dataの定義
y = pm.ConstantData('y', value=data['val_z'].values, dims='data')
### 事前分布
# 事前分布
sigmaTheta = pm.HalfCauchy('sigmaTheta', beta=5, dims='combi')
theta = pm.Normal('theta', mu=0, sigma=sigmaTheta, dims='combi')
sigma = pm.HalfCauchy('sigma', beta=5, dims='judge')
### 尤度
likelohood = pm.Normal('likelihood',
mu=theta[combi_idx], sigma=sigma[judge_idx],
observed=y, dims='data')【モデル注釈】省略
2.モデルの外観の確認
### モデルの表示
model2【実行結果】
シンプルなモデルです。

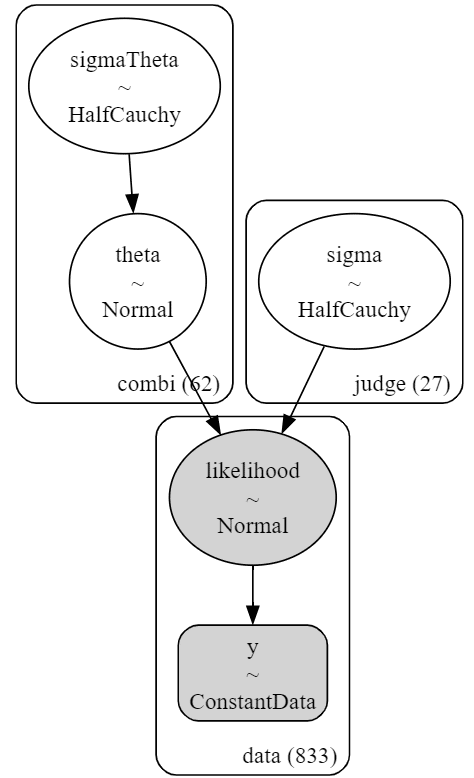
# モデルの可視化
pm.model_to_graphviz(model2)【実行結果】
シンプルなモデルです。
3.事後分布からのサンプリング
乱数生成数(draws)はテキストよりも少なめです。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ50秒でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 50秒
with model2:
idata2 = pm.sample(draws=5000, tune=5000, chains=4, target_accept=0.9,
nuts_sampler='numpyro', random_seed=1235)【実行結果】省略
4.サンプリングデータの確認
$${\hat{R}}$$、トレースプロットを確認します。
事後分布の収束確認は$${\hat{R}\leq 1.1}$$としています。
### r_hat>1.1の確認
rhat_idata2 = az.rhat(idata2)
(rhat_idata2>1.1).sum()【実行結果】
$${\hat{R} >1.1}$$のパラメータは「0」件です。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。
トレースプロットです。
### トレースプロットの表示
pm.plot_trace(idata2, compact=True, combined=True, figsize=(12, 7))
plt.tight_layout();【実行結果】
密集する様子は、パラメータ同士が競い合っているかのように見えます。
発散を示す下部の黒い線(通称:バーコード)が多いのが気になります。
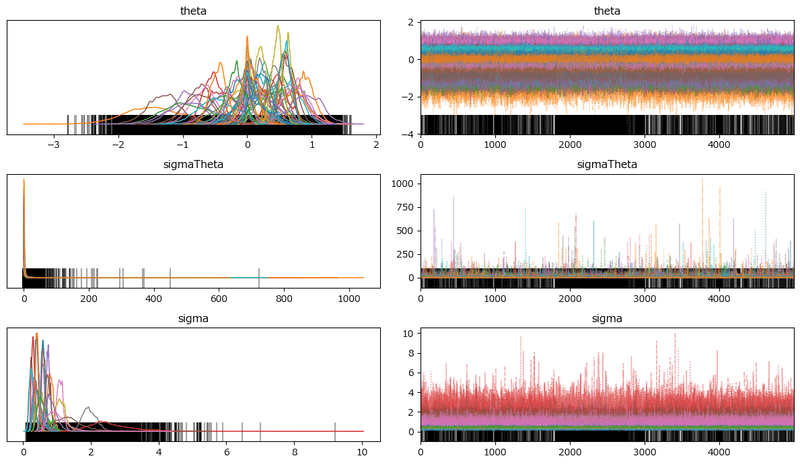
5.審査員のくせ評価モデルの結果
テキストの表11.3に相当する「おもしろさ($${\theta_i}$$)の事後分布の上位5組の要約統計量」を算出します。
pm.summary()関数で対応します。
### おもしろさの事後分布の上位5組の要約統計情報 ★表11.3に対応
(pm.summary(idata2, hdi_prob=0.95, kind='stats', var_names=['theta'])
.sort_values('mean', ascending=False).head(5).reset_index().round(2))【実行結果】
テキストの順番と若干相違します。
平均(mean、テキストのEAP)に関するテキストとの若干ずれが、順番に影響したようです。
標準偏差(sd、テキストのpost.sd)はテキストと若干ずれがあります。
なお、下限・上限については、テキストが信用区間(確信区間)を使用、この記事はHDIを使用しているため、相違する結果となります。

続いて、テキストの表11.4に相当する「標準偏差の事後分布の中央値・95%信用区間」を算出します。
### 標準偏差の事後分布の中央値および95%信用区間 ★表11.4に対応
## 推論データから要約統計情報を計算する関数の定義
def calc_stat(i, idata):
tmp = idata.posterior.sigma[:, :, i].data.flatten()
return [judge_cat[i], np.median(tmp), np.quantile(tmp, 0.025),
np.quantile(tmp, 0.975)]
## sigma_statsデータフレームの作成
# データフレームの初期化
sigma_stats = pd.DataFrame()
# top5の順に要約統計情報を計算してデータフレームに追加
for i in set(judge_idx):
tmp_stats = calc_stat(i, idata2)
sigma_stats = pd.concat([sigma_stats, pd.DataFrame(tmp_stats).T], axis=0)
# カラム名とインデックスの補正(型をfloatに変換の上、中央値で降順ソート)
sigma_stats.columns = ['審査員', '中央値', '2.5%', '97.5%']
sigma_stats = sigma_stats.astype({'中央値': float, '2.5%': float, '97.5%': float})
sigma_stats = sigma_stats.sort_values(by='中央値', ascending=False)
sigma_stats.reset_index(drop=True, inplace=True)
# 要約統計量の表示
print('【標準偏差の事後分布の中央値と95%信用区間】')
display(sigma_stats.head(3).round(2))
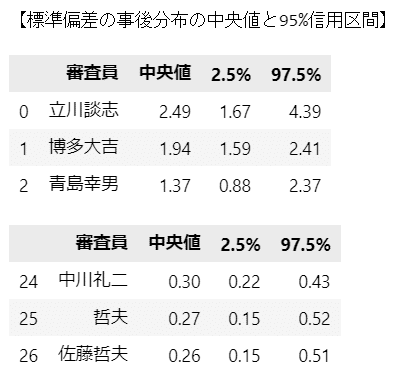
display(sigma_stats.tail(3).round(2))【実行結果】
テキストの順番と一致しました。
中央値、信用区間の値はテキストと若干ずれがあります。
先ほどの審査員ごとの箱ひげ図で、区間幅の大きかった(つまり得点のバラツキが大きかった)審査員が上位にきています。
6.推論データ(idata)の保存
推論データを再利用する場合に備えてファイルに保存しましょう。
idata2をpickleで保存します。
### idataの保存 pickle
file = r'idata2_ch11.pkl'
with open(file, 'wb') as f:
pickle.dump(idata2, f)読み込みコードは次のとおりです。
### idataの読み込み pickle
file = r'idata2_ch11.pkl'
with open(file, 'rb') as f:
idata2_load = pickle.load(f)
モデル3:審査員の基準効果モデル
テキスト「11.4 審査員の基準効果モデル」のモデルです。
モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
添字$${i}$$はコンビのインデックス、$${j}$$は審査員のインデックスです。
$$
\begin{align*}
\sigma_{\theta} &\sim \text{HalfCaushy}\ (\text{beta}=5)\\
\sigma_{\gamma} &\sim \text{HalfCaushy}\ (\text{beta}=5)\\
\sigma_i &\sim \text{HalfCauchy}\ (\text{beta}=5) \\
\theta_i &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=\sigma_{\theta}) \\
\gamma_j &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=\sigma_{\gamma}) \\
likelihood &\sim \text{Normal}\ (\text{mu}=\theta_i + \gamma_j,\ \text{sigma}=\sigma_i) \\
\end{align*}
$$
1.モデルの定義
### モデルの定義
with pm.Model() as model3:
### データ関連定義
# coordの定義
model3.add_coord('data', values=data.index, mutable=True)
model3.add_coord('combi', values=combi_cat, mutable=True)
model3.add_coord('judge', values=judge_cat, mutable=True)
# dataの定義
y = pm.ConstantData('y', value=data['val_z'].values, dims='data')
### 事前分布
# θ_i, σ_θ
sigmaTheta = pm.HalfCauchy('sigmaTheta', beta=5)
theta = pm.Normal('theta', mu=0, sigma=sigmaTheta, dims='combi')
# γ_j, σ_γ
sigmaGamma = pm.HalfCauchy('sigmaGamma', beta=5)
gamma = pm.Normal('gamma', mu=0, sigma=sigmaGamma, dims='judge')
# σ_i
sigma = pm.HalfCauchy('sigma', beta=5, dims='combi')
### 尤度
likelohood = pm.Normal('likelihood',
mu=theta[combi_idx] + gamma[judge_idx],
sigma=sigma[combi_idx], observed=y, dims='data')【モデル注釈】省略
2.モデルの外観の確認
### モデルの表示
model3【実行結果】
まだまだシンプルなモデルです。

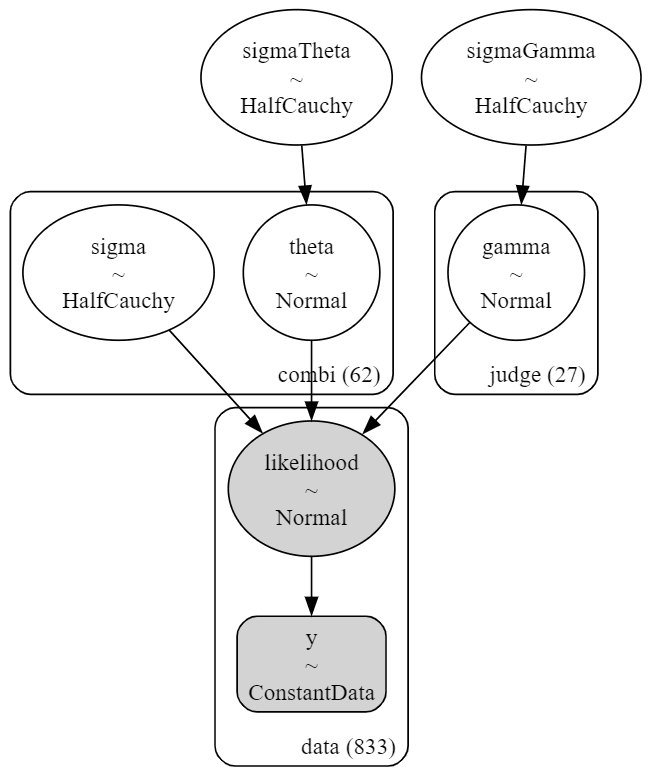
# モデルの可視化
pm.model_to_graphviz(model2)【実行結果】
まだまだシンプルなモデルです。
3.事後分布からのサンプリング
乱数生成数(draws)はテキストよりも少なめです。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ20秒でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 20秒
with model3:
idata3 = pm.sample(draws=5000, tune=5000, chains=4, target_accept=0.9,
nuts_sampler='numpyro', random_seed=1235)【実行結果】省略
4.サンプリングデータの確認
$${\hat{R}}$$、トレースプロットを確認します。
事後分布の収束確認は$${\hat{R}\leq 1.1}$$としています。
### r_hat>1.1の確認
rhat_idata3 = az.rhat(idata3)
(rhat_idata3>1.1).sum()【実行結果】
$${\hat{R} >1.1}$$のパラメータは「0」件です。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

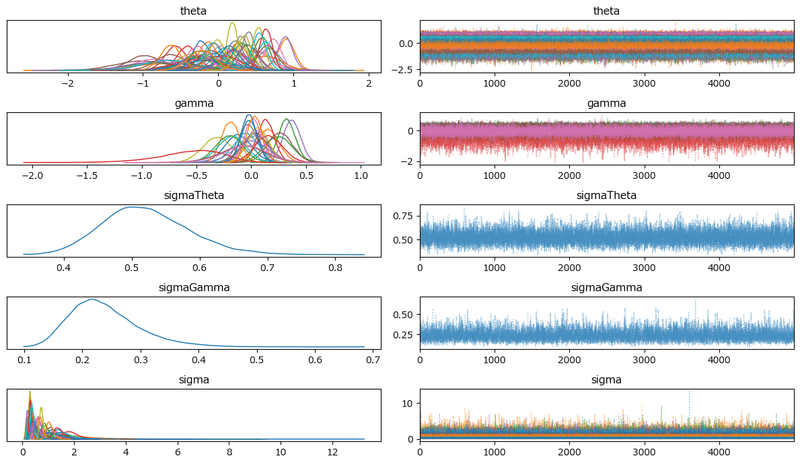
トレースプロットです。
### トレースプロットの表示
pm.plot_trace(idata3, compact=True, combined=True, figsize=(12, 7))
plt.tight_layout();【実行結果】
密集する様子は、パラメータ同士が競い合っているかのように見えます。
5.審査員の基準効果モデルの結果
テキストの表11.5に相当する「おもしろさ($${\theta_i}$$)の事後分布の上位5組の要約統計量」を算出します。
pm.summary()関数で対応します。
### おもしろさの事後分布の上位5組の要約統計情報 ★表11.5に対応
(pm.summary(idata3, hdi_prob=0.95, kind='stats', var_names=['theta'])
.sort_values('mean', ascending=False).head(5).reset_index().round(2))【実行結果】
テキストの順番とかなり相違するようです。
平均(mean, テキストのEAP)がテキストよりも下振れしている模様です。
理由は不明です…。
なお、下限・上限については、テキストが信用区間(確信区間)を使用、この記事はHDIを使用しているため、相違する結果となります。

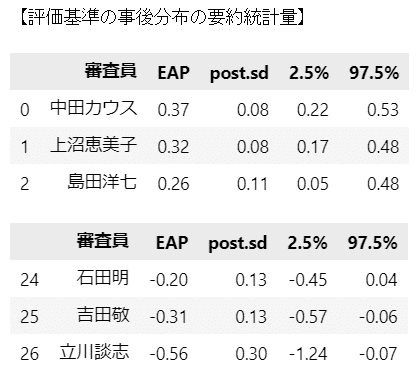
続いて、テキストの表11.6に相当する「評価基準の事後分布の要約統計量」を算出します。
### 評価基準の事後分布の要約統計情報 ★表11.6に対応
## 推論データから要約統計情報を計算する関数の定義
def calc_stat(i, idata):
tmp = idata.posterior.gamma[:, :, i].data.flatten()
return [judge_cat[i], np.mean(tmp), np.std(tmp), np.quantile(tmp, 0.025),
np.quantile(tmp, 0.975)]
## gamma_statsデータフレームの作成
# データフレームの初期化
gamma_stats = pd.DataFrame()
# top5の順に要約統計情報を計算してデータフレームに追加
for i in set(judge_idx):
tmp_stats = calc_stat(i, idata3)
gamma_stats = pd.concat([gamma_stats, pd.DataFrame(tmp_stats).T], axis=0)
# カラム名とインデックスの補正(型をfloatに変換の上、EAPで降順ソート)
gamma_stats.columns = ['審査員', 'EAP', 'post.sd', '2.5%', '97.5%']
gamma_stats = gamma_stats.astype({'EAP': float, 'post.sd': float,
'2.5%': float, '97.5%': float})
gamma_stats = gamma_stats.sort_values(by='EAP', ascending=False)
gamma_stats.reset_index(drop=True, inplace=True)
## 要約統計量の表示
print('【評価基準の事後分布の要約統計量】')
display(gamma_stats.head(3).round(2))
display(gamma_stats.tail(3).round(2))【実行結果】
こちらはテキストの順番と一致しました。
中央値、信用区間の値はテキストとほぼ一致しています。
6.推論データ(idata)の保存
推論データを再利用する場合に備えてファイルに保存しましょう。
idata3をpickleで保存します。
### idataの保存 pickle
file = r'idata3_ch11.pkl'
with open(file, 'wb') as f:
pickle.dump(idata3, f)読み込みコードは次のとおりです。
### idataの読み込み pickle
file = r'idata3_ch11.pkl'
with open(file, 'rb') as f:
idata3_load = pickle.load(f)
モデル4:開催回数効果モデル
テキスト「11.5 開催回数効果モデル」のモデルです。
モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
添字$${i}$$はコンビのインデックス、$${j}$$は審査員のインデックス、$${o}$$は開催回数のインデックスです。
$$
\begin{align*}
\sigma_{\theta} &\sim \text{HalfCaushy}\ (\text{beta}=5)\\
\sigma_{\gamma} &\sim \text{HalfCaushy}\ (\text{beta}=5)\\
\sigma_{\zeta} &\sim \text{HalfCaushy}\ (\text{beta}=5)\\
\sigma_e &\sim \text{HalfCauchy}\ (\text{beta}=5) \\
\theta_i &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=\sigma_{\theta}) \\
\gamma_j &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=\sigma_{\gamma}) \\
\zeta_o &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=\sigma_{\zeta}) \\
likelihood &\sim \text{Normal}\ (\text{mu}=\theta_i + \gamma_j + \zeta_o,\ \text{sigma}=\sigma_e) \\
\end{align*}
$$
1.モデルの定義
### モデルの定義
with pm.Model() as model4:
### データ関連定義
# coordの定義
model4.add_coord('data', values=data.index, mutable=True)
model4.add_coord('combi', values=combi_cat, mutable=True)
model4.add_coord('judge', values=judge_cat, mutable=True)
model4.add_coord('times', values=times_cat, mutable=True)
# dataの定義
y = pm.MutableData('y', value=data['val_z'].values, dims='data')
### 事前分布
# θ_i, σ_θ
sigmaTheta = pm.HalfCauchy('sigmaTheta', beta=5)
theta = pm.Normal('theta', mu=0, sigma=sigmaTheta, dims='combi')
# γ_j, σ_γ
sigmaGamma = pm.HalfCauchy('sigmaGamma', beta=5)
gamma = pm.Normal('gamma', mu=0, sigma=sigmaGamma, dims='judge')
# ζ_j, σ_ζ
sigmaZeta = pm.HalfCauchy('sigmaZeta', beta=5)
zeta = pm.Normal('zeta', mu=0, sigma=sigmaZeta, dims='times')
# σ_e
sigmaE = pm.HalfCauchy('sigmaE', beta=5)
### 尤度
likelohood = pm.Normal('likelihood',
mu=theta[combi_idx] + gamma[judge_idx] + zeta[times_idx],
sigma=sigmaE, observed=y, dims='data')【モデル注釈】省略
2.モデルの外観の確認
### モデルの表示
model4【実行結果】
事前分布が多くなりました。

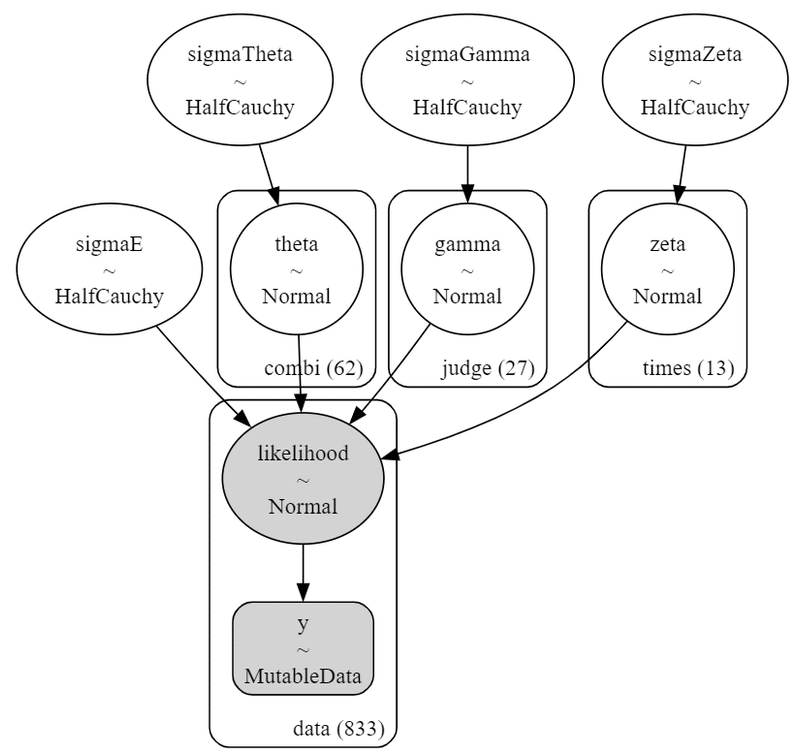
# モデルの可視化
pm.model_to_graphviz(model4)【実行結果】
コンビ(combi)、審査員(judge)、開催回(times)ごとにパラメータが設定されている様子がよく分かります。
3.事後分布からのサンプリング
乱数生成数(draws)はテキストよりも少なめです。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ20秒でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 20秒
with model4:
idata4 = pm.sample(draws=5000, tune=5000, chains=4, target_accept=0.9,
nuts_sampler='numpyro', random_seed=1235)【実行結果】省略
4.サンプリングデータの確認
$${\hat{R}}$$、トレースプロットを確認します。
事後分布の収束確認は$${\hat{R}\leq 1.1}$$としています。
### r_hat>1.1の確認
rhat_idata4 = az.rhat(idata4)
(rhat_idata4>1.1).sum()【実行結果】
$${\hat{R} >1.1}$$のパラメータは「0」件です。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

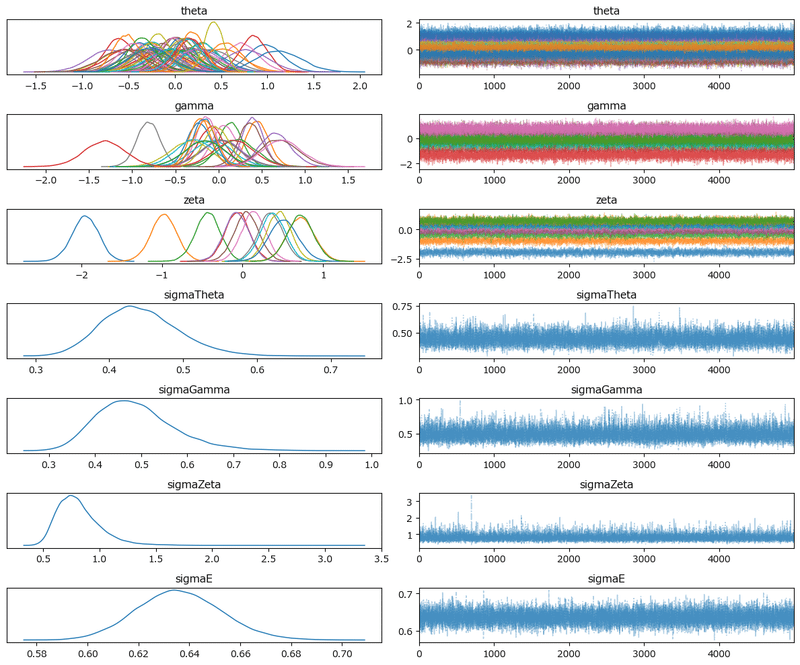
トレースプロットです。
### トレースプロットの表示
pm.plot_trace(idata4, compact=True, combined=True, figsize=(12, 10))
plt.tight_layout();【実行結果】
きれいな図は収束している様子をよく表しています。
5.開催回数効果モデルの結果
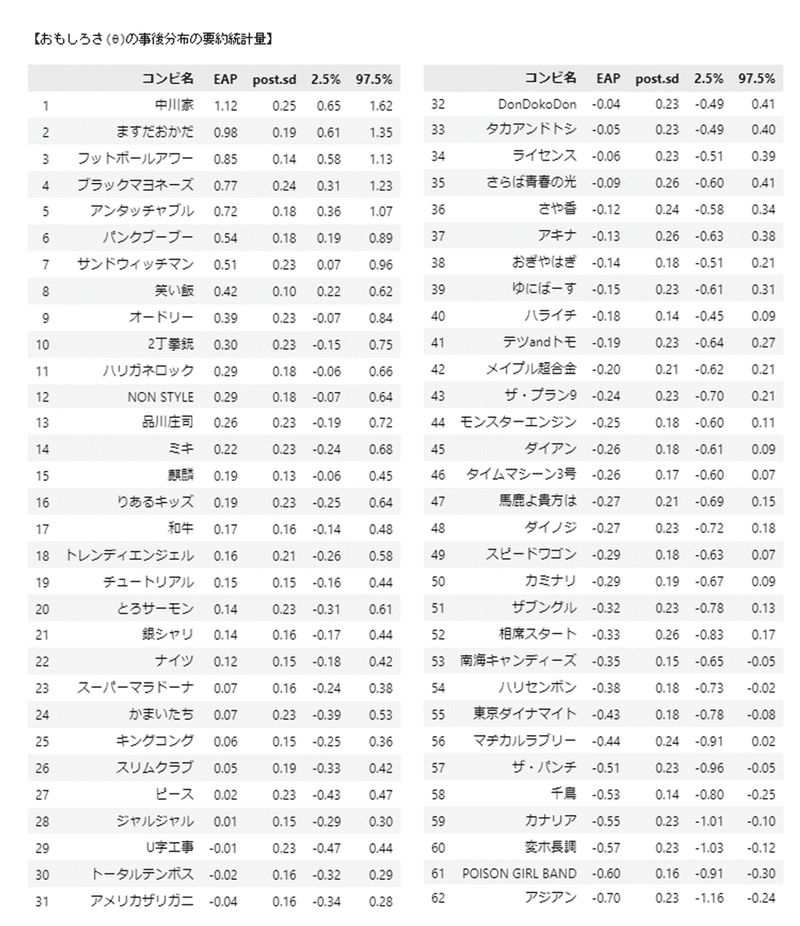
テキストの表11.7に相当する「おもしろさ($${\theta_i}$$)の事後分布の要約統計量」を算出します。
### おもしろさの事後分布の要約統計情報 ★表11.7に対応
## 推論データから要約統計情報を計算する関数の定義
def calc_stat(i, idata):
tmp = idata.posterior.theta[:, :, i].data.flatten()
return [combi_cat[i], np.mean(tmp), np.std(tmp), np.quantile(tmp, 0.025),
np.quantile(tmp, 0.975)]
## theta_statsデータフレームの作成
# データフレームの初期化
theta_stats = pd.DataFrame()
# top5の順に要約統計情報を計算してデータフレームに追加
for i in set(combi_idx):
tmp_stats = calc_stat(i, idata4)
theta_stats = pd.concat([theta_stats, pd.DataFrame(tmp_stats).T], axis=0)
# カラム名とインデックスの補正(型をfloatに変換の上、EAPで降順ソート)
theta_stats.columns = ['コンビ名', 'EAP', 'post.sd', '2.5%', '97.5%']
theta_stats = theta_stats.astype({'EAP': float, 'post.sd': float,
'2.5%': float, '97.5%': float})
theta_stats = theta_stats.sort_values(by='EAP', ascending=False)
theta_stats.reset_index(drop=True, inplace=True)
theta_stats.index = theta_stats.index + 1
## 要約統計量の表示
print('【おもしろさ(θ)の事後分布の要約統計量】')
display(theta_stats.head(31).round(2))
display(theta_stats.tail(31).round(2))【実行結果】
初期の優勝コンビが上位にきているようです。
なお、テキストの順番といくつか相違しています。
テキストは小数点第2位で四捨五入してから順番の並び替え処理を行っていますが、このコードでは並び替え処理後に小数点丸め処理を行っています。
この処理の違いの影響がありそうです。
実質面での分析はぜひテキストをご覧ください!
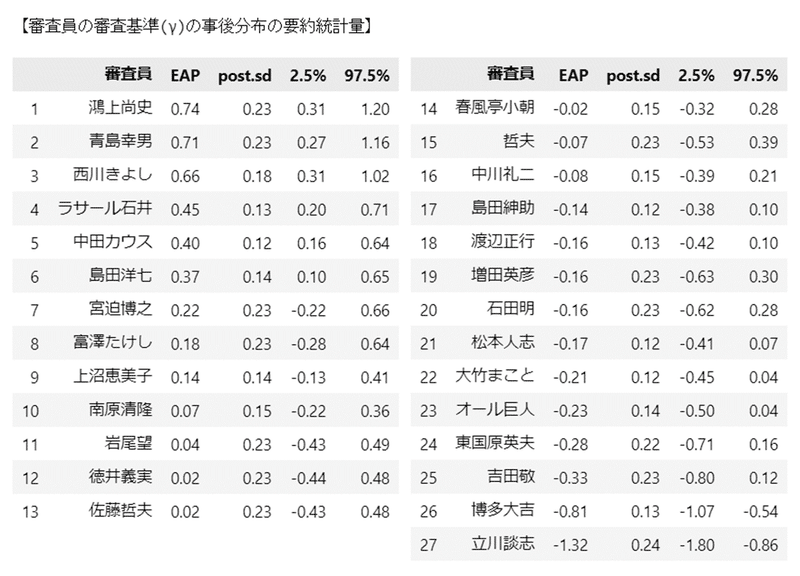
続いて、テキストの表11.8に相当する「審査員の審査基準($${\gamma_j}$$)の事後分布の要約統計量」を算出します。
### 審査員の審査基準の事後分布の要約統計情報 ★表11.8に対応
## 推論データから要約統計情報を計算する関数の定義
def calc_stat(i, idata):
tmp = idata.posterior.gamma[:, :, i].data.flatten()
return [judge_cat[i], np.mean(tmp), np.std(tmp), np.quantile(tmp, 0.025),
np.quantile(tmp, 0.975)]
## gamma_statsデータフレームの作成
# データフレームの初期化
gamma_stats = pd.DataFrame()
# top5の順に要約統計情報を計算してデータフレームに追加
for i in set(judge_idx):
tmp_stats = calc_stat(i, idata4)
gamma_stats = pd.concat([gamma_stats, pd.DataFrame(tmp_stats).T], axis=0)
# カラム名とインデックスの補正(型をfloatに変換の上、EAPで降順ソート)
gamma_stats.columns = ['審査員', 'EAP', 'post.sd', '2.5%', '97.5%']
gamma_stats = gamma_stats.astype({'EAP': float, 'post.sd': float,
'2.5%': float, '97.5%': float})
gamma_stats = gamma_stats.sort_values(by='EAP', ascending=False)
gamma_stats.reset_index(drop=True, inplace=True)
gamma_stats.index = gamma_stats.index + 1
## 要約統計量の表示
print('【審査員の審査基準(γ)の事後分布の要約統計量】')
display(gamma_stats.head(13).round(2))
display(gamma_stats.tail(14).round(2))【実行結果】
テキストの順番といくつか相違しています。
こちらも並び替え処理のタイミングが順番の相違に影響していると思われます。
実質面での分析はぜひテキストをご覧ください!
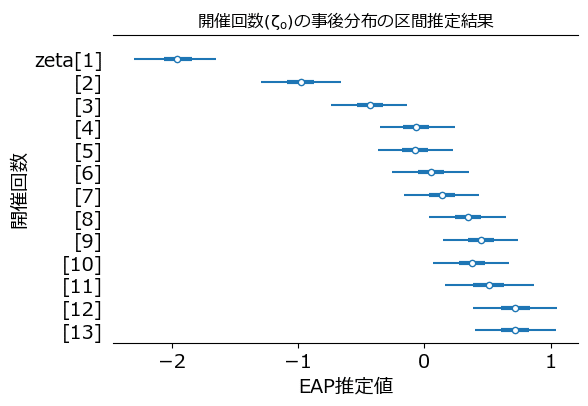
6.開催回数の効果
テキストの図11.1に相当する「開催回数($${\zeta_o}$$)と事後分布の区間推定」を描画します。
フォレストプロットを利用しました。
### フォレストプロットの描画 ★図11.1に対応
ax = pm.plot_forest(idata4, var_names=['zeta'], hdi_prob=0.95, combined=True,
figsize=(6,4))
ax[0].set_title(r'開催回数($\zeta_o$)の事後分布の区間推定結果')
ax[0].set_xlabel('EAP推定値', fontsize=14)
ax[0].set_ylabel('開催回数', fontsize=14);【実行結果】
開催初期はマイナス値であり、評価得点の平均を引き下げる効果が見られました。
7.おもしろさの信頼性の描画
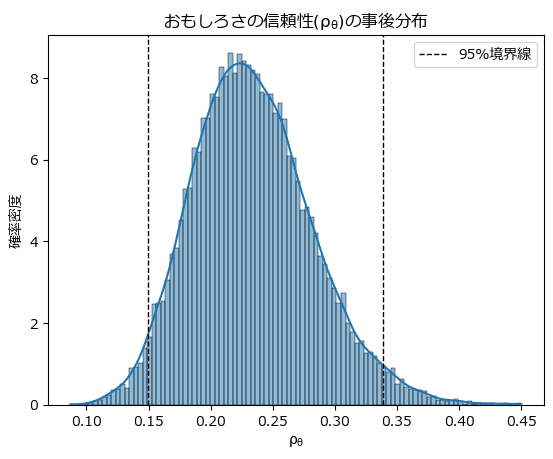
テキストの図11.2に相当する「おもしろさの信頼性($${\rho_{\theta}}$$)の事後分布」を描画します。
seaborn の histplot を利用します。
### おもしろさの信頼性の事後分布 ★図11.2に対応
# ρ_θの計算
sigma_theta_data = idata4.posterior.sigmaTheta.data.flatten()
sigma_gamma_data = idata4.posterior.sigmaGamma.data.flatten()
sigma_e_data = idata4.posterior.sigmaE.data.flatten()
rho = (sigma_theta_data**2
/ (sigma_theta_data**2 + sigma_gamma_data**2 + sigma_e_data**2))
# 95%区間の計算
q025 = np.quantile(rho, 0.025)
q975 = np.quantile(rho, 0.975)
# ρのヒストグラムの描画
ax = sns.histplot(rho, bins=100, stat='density', kde=True)
# 95%境界線の描画
ax.axvline(q025, lw=1, ls='--', color='black', label='95%境界線')
ax.axvline(q975, lw=1, ls='--', color='black')
# 修飾
ax.set_title(r'おもしろさの信頼性($\rho_{\theta}$)の事後分布')
ax.set_xlabel(r'$\rho_{\theta}$')
ax.set_ylabel('確率密度')
ax.legend();【実行結果】
テキストの分析をお借りすると、このモデルが真のモデルであると仮定する場合の議論として、「漫才のおもしろさによって決定されるのは、大きく見積もって3割ほどである」ようです。
95%信頼区間の上端が約$${0.34}$$。
8.推論データ(idata)の保存
推論データを再利用する場合に備えてファイルに保存しましょう。
idata4をpickleで保存します。
### idataの保存 pickle
file = r'idata4_ch11.pkl'
with open(file, 'wb') as f:
pickle.dump(idata4, f)読み込みコードは次のとおりです。
### idataの読み込み pickle
file = r'idata4_ch11.pkl'
with open(file, 'rb') as f:
idata4_load = pickle.load(f)以上で第11章は終了です。
おわりに
シンプルなモデル
シンプルなモデルだからこその説得力を感じられる、とても勉強になったモデリングでした。
正規分布が威力を発揮するモデルは無双感がハンパないです!
世界がベル型+ホワイトノイズで生成されていたなら・・・

シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で4つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
2.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析トピックを PythonとPyMC Ver.5で取り組みます。
豊富なテーマ(お題)を実践することによって、PythonとPyMCの基礎体力づくりにつながる、そう信じています。
日々、Web検索に勤しみ、時系列モデルの理解、Pythonパッケージの把握、R・Stanコードの翻訳に励んでいます!
このシリーズがPython時系列分析の入門者の参考になれば幸いです🍀
3.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learn と PyTorch の教科書です。
よかったらぜひ、お試しくださいませ。
4.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Python のコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
ベイズ書籍の実践記録も掲載中です。
最後までお読みいただきまして、ありがとうございました。
この記事が気に入ったらサポートをしてみませんか?
