第７章「異常検知の実践例」

書籍の著者　笛田薫 先生、江崎剛史 先生、李鍾賛 先生

この記事は、テキスト「Pythonではじめる異常検知入門」の第７章「異常検知の実践例」の 7-2 節「時系列データの異常検知」の通称「寄り道写経」を取り扱います。

テキストは平均気温時系列データで ARIMA モデルを構築しています。
この記事は飛行機乗客者数データで SARIMA モデル（もどき）にトライします🛫
第６章の分も合わせて、時系列データの異常検知を楽しみます！
ではテキストを開いて異常検知の旅に出発です🚀

このシリーズは書籍「Pythonではじめる異常検知入門」（科学情報出版、「テキスト」と呼びます）の異常検知の理論・数式とPythonプログラムを参考にしながら、テキストにはプログラムの紹介が無いけれども気になったテーマ、または、テキストのプログラム以外の方法を試したいテーマを「実験的」にPythonコード化する寄り道写経ドキュメンタリーです。

はじめに

テキスト「Pythonではじめる異常検知入門」のご紹介

テキストは、2023年4月に発売された異常検知の入門書です。
数式展開あり、Python実装ありのテキストなのです。
Jupyter Notebook 形式のソースコードと csv 形式のデータは、書籍購入者限定特典として書籍掲載のURLからダウンロードできます。

引用表記

この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
【出典】
「Pythonではじめる異常検知入門－基礎から実践まで－」初版、著者 笛田薫／江崎剛史／李鍾賛、オーム社

記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます！

第７章 異常検知の実践例

Jupyter Notebook 形式（拡張子 .ipynb）でPythonコードを書きます。

テキストのこの章では、次の３種類の異常検知をPythonで実践します。

この記事は ③ の時系列データの異常検知の寄り道写経を行います。
テキストの分析の流れを参考にさせていただき、テキストと異なるデータを用いて、時系列データの異常検知に近づきたいと考えています。
テキストが扱う時系列異常検知の条件「残差が正規分布に従う仮定」のクリアが必須です！

インポート

### インポート

# 数値・確率計算
import pandas as pd
import numpy as np
import scipy.stats as stats

# 時系列
from statsmodels.tsa.seasonal import seasonal_decompose
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.tsa.stattools import adfuller
from pmdarima import auto_arima

# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'

# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')

Google Colab をご利用の場合は「描画」箇所を以下のように差し替えてください。

!pip install japanize_matplotlib
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns

データの読み込み

R 言語の標準データセットに含まれる「AirPassengers」を利用します。
1949 年から 1960 年までの米国・国際線月次乗客数です。
次の R データセットサイトの No. 451 です。

【引用元サイト】

Webサイトから直接pandasのデータフレームへ読み込みします。

### データの取得
# Air Passengers
# https://vincentarelbundock.github.io/Rdatasets/doc/datasets/AirPassengers.html

# データセットを取得するWebサイトのURL
URL = (r'https://vincentarelbundock.github.io/Rdatasets/csv/datasets/'
       r'AirPassengers.csv')
# データセットの読み込み
passengers = pd.read_csv(URL, usecols=[1, 2]) 
# time列を日付に変更
passengers['time'] = pd.date_range(start='1949-01', periods=144, freq='MS')
# time列をindex
passengers.set_index('time', inplace=True)
# データフレームの表示
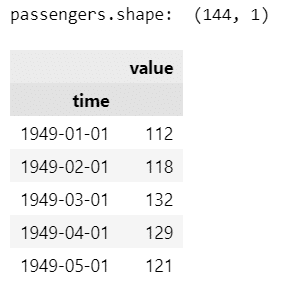
print('passengers.shape: ', passengers.shape)
display(passengers.head())

【実行結果】
期間（行数）は1949年1月からの144か月分（12年分）、valueは1か月あたりの乗客数です。

データの可視化

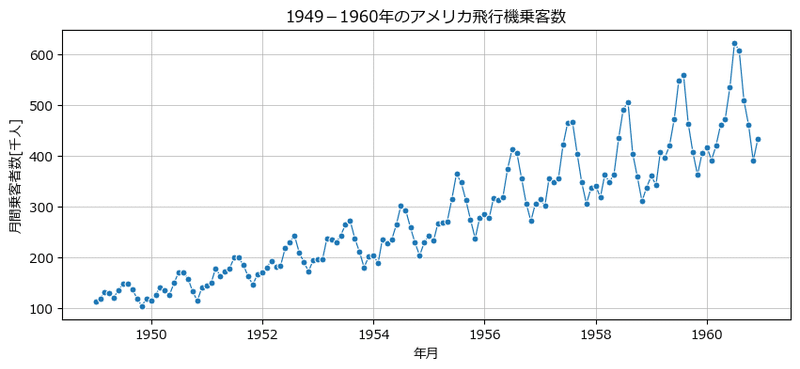
時系列の折れ線グラフを描画します。

### 可視化
fig, ax = plt.subplots(figsize=(10, 4))
sns.lineplot(data=passengers, markers='o', ms=5, lw=0.9, legend=False, ax=ax)
ax.set(xlabel='年月', ylabel='月間乗客者数[千人]',
       title='1949－1960年のアメリカ飛行機乗客数')
ax.grid(lw=0.5);

【実行結果】
右肩上がりの「トレンド」と12か月周期の「季節性」がくっきり見られます！

季節分解して変動要素別にプロットしましょう。
statsmodels の seasonal_decompose() を用いて季節分解します。
周期は12です。

### 季節成分の分解

## 季節分解の実行（加法モデル）
result = seasonal_decompose(x=passengers, model='additive', period=12)

## 描画処理
# 描画領域の設定
fig, ax = plt.subplots(4, 1, figsize=(7, 7), sharex=True)
# 原系列の描画
ax[0].plot(result.observed, lw=0.8)
ax[0].set(ylabel='原系列')
ax[0].grid(lw=0.5)
# トレンドの描画
ax[1].plot(result.trend, lw=0.8)
ax[1].set(ylabel='トレンド')
ax[1].grid(lw=0.5)
# 季節調整（周期性）の描画
ax[2].plot(result.seasonal, lw=0.8)
ax[2].set(ylabel='季節調整')
ax[2].grid(lw=0.5)
# 残差の描画
ax[3].plot(result.resid, 'o', ms=5, mec='white', alpha=0.7)
ax[3].axhline(0, color='tab:red', ls='--')
ax[3].set(ylabel='残差')
ax[3].grid(lw=0.5)
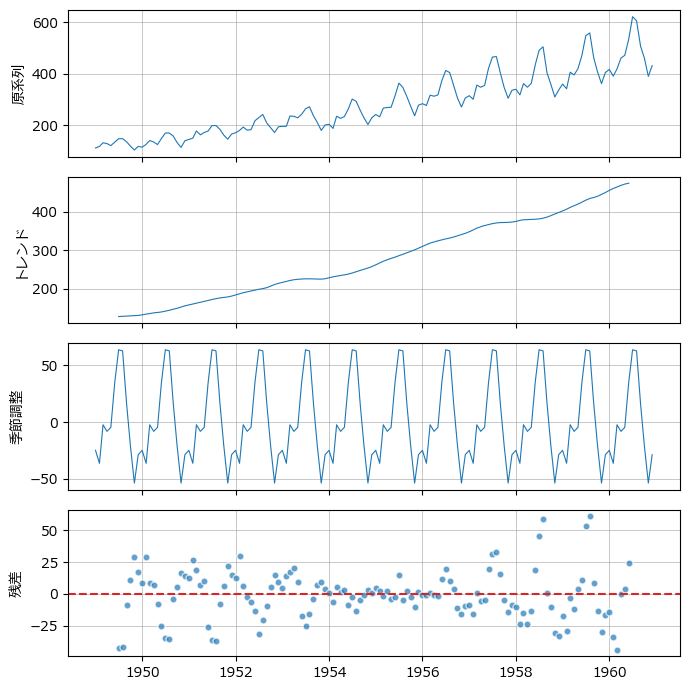
plt.tight_layout();

【実行結果】
右肩上がりの「トレンド」と12か月周期の「季節性」を確認できました。
季節性を考慮するモデルの検討が必要そうです。
残差のバラツキには何となく12か月周期の残骸が含まれている感じがします。

データセットの準備

学習データとテストデータに分割します。
飛行機乗客数データの時系列データ分析全般について、セールスアナリティクス社様のブログを参考にさせていただきました。
ありがとうございます！

学習データを最初の132か月（11年）、テストデータを最後の12か月（1年）に分割します。

### 学習データとテストデータに分離 1949-1959:学習用, 1960:テスト用

# 前半の132か月を学習用(ts)、最後の12ヶ月をテスト用(ts_test)に分割
train_df = passengers.iloc[:-12]
test_df = passengers.iloc[-12:]

# 分割結果の表示
print('train_df.shape: ', train_df.shape)
display(train_df.head())
print('test_df.shape : ', test_df.shape)
display(test_df.head())

【実行結果】

学習データの外観を確認します。
まずは要約統計量の表示です。

### 要約統計量の表示
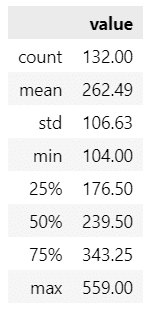
display(train_df.describe().round(2))

【実行結果】
最小値 104、最大値 559、平均値 262、中央値 234 です。

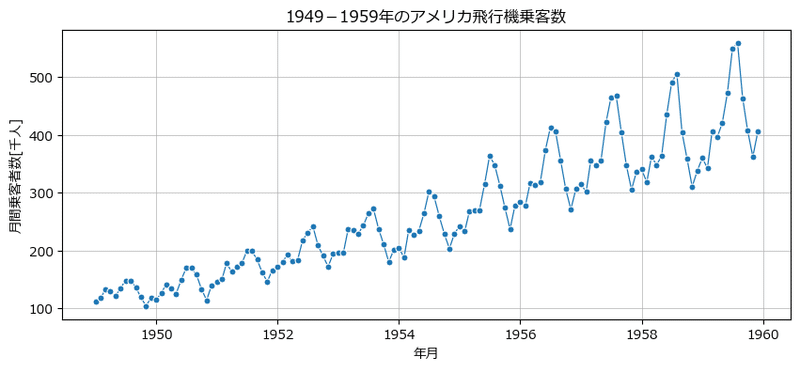
学習データの時系列折れ線グラフを描画します。
テキスト図7-11に相当します。

### 時系列プロット
fig, ax = plt.subplots(figsize=(10, 4))
sns.lineplot(data=train_df, markers='o', ms=5, lw=0.9, legend=None, ax=ax)
ax.set(xlabel='年月', ylabel='月間乗客者数[千人]',
       title='1949－1959年のアメリカ飛行機乗客数')
ax.grid(lw=0.5)

【実行結果】

時系列データの分析

テキストの分析手順に沿って、学習データの時系列の特性を掴みます。

■ 自己相関の散布図
ラグ１の自己相関を散布図で確認します。
テキスト図7-12に相当します。

### 散布図の表示

# 相関係数の算出
r = np.corrcoef(train_df.iloc[:-1, 0], train_df.iloc[1:, 0])[0, 1]
# 描画領域の指定
fig, ax = plt.subplots(figsize=(5, 4))
# 散布図の描画 回帰直線付き
sns.regplot(x=train_df[:-1], y=train_df[1:],
            line_kws={'color': 'tomato'},
            scatter_kws={'ec': 'white', 's': 80})
# 修飾
ax.set(xlabel='$y_{t-1}$ [千人]', ylabel='$y_t$ [千人]',
       title=f'ラグ１の散布図\n相関係数:{r:.3f}')
plt.grid(lw=0.5);

【実行結果】
横軸が１か月前の乗客数、縦軸が当月の乗客数の散布図です。

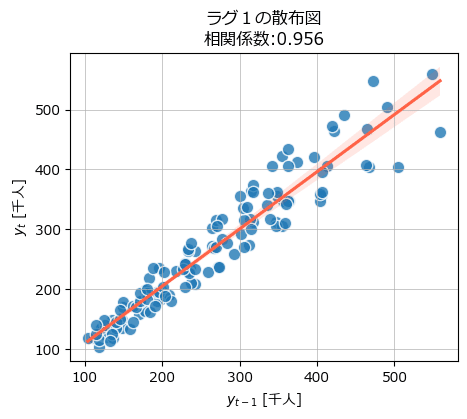
かなり強い正の相関関係があります。
データ点は回帰直線にはまっている感じもしますし、400人を超えるあたりから回帰直線との乖離が大きくなっている感じもします。

■ コレログラムと偏自己相関プロットの描画
自己相関関数と偏自己相関関数を描画します。
自己相関関数の図はコレログラムと呼ばれます。
statsmodels の plot_acf() でコレログラムを描き、plot_pacf() で偏自己相関関数を描画します。
テキスト図7-13に相当します。

### 自己相関・偏自己相関のプロット

# 描画領域の設定
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 3))
# コレログラムの描画
plot_acf(train_df, lags=50, ax=ax1, title='コレログラム')
ax1.set(xlabel='Lag', ylabel='ACF', ylim=(-1, 1.2))
ax1.grid(lw=0.5)
# 偏自己相関プロットの描画
plot_pacf(train_df, lags=50, ax=ax2, title='偏自己相関プロット')
ax2.set(xlabel='Lag', ylabel='PACF', ylim=(-1, 1.2))
ax2.grid(lw=0.5)
plt.tight_layout();

【実行結果】

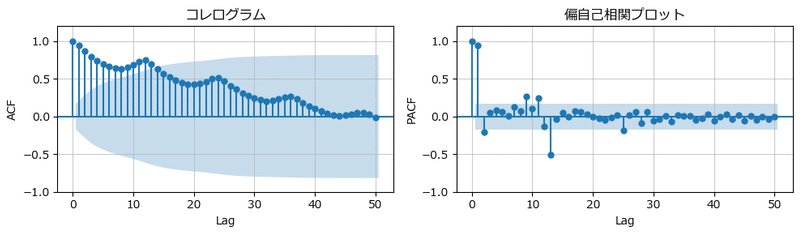
コレログラムより、12か月まで有意な自己相関関数が見られます。
偏自己相関関数からは、1か月前（ラグ１）と13か月前（ラグ13）に有意な値が見られます。
１階階差と12階階差（12か月周期の1階階差）を考慮するのがいいかもしれません。

■ 定常性の検定
定常性に関するADF検定を行います。
帰無仮説は「データは非定常である」です。
statsmodels の adfuller を利用します。

### 学習データのADF検定
# 帰無仮説：データは単位根を持つ（非定常である）

# ADF検定（原系列）
adf = adfuller(train_df)
print('原系列　　　:', round(adf[1], 3))

# ADF検定（１階差分列）
adf_diff = adfuller(train_df.diff(1)[1:])
print('１階差分系列:', round(adf_diff[1], 3))

# ADF検定（1階差分&12階差分列）
adf_diff = adfuller(train_df.diff(1).diff(12)[13:])
print('1階&12階系列:', round(adf_diff[1], 3))

【実行結果】
ADF検定の結果の$${p}$$値を表示しています。

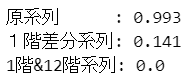
素のデータである原系列は 99.3% であり（帰無仮説を棄却できないでしょうから）非定常と考えられます。
１階差分系列は 14.1% 。有意水準を10%においても（帰無仮説を棄却できないので）非定常と考えられます。
1階差分系列から更に12階差分を取った１階＆12階階差系列は 0.0 %であり、（帰無仮説を棄却できると思われますので）定常！と考えられます。

ARIMAモデルの１階差分と季節性の１階差分（12階分）を考えるのは妥当そうです。

SARIMAモデルの構築

季節性を考慮できる SARIMA モデルを構築します！

■ 最適モデルの探索
pmdarima パッケージの auto_arima を利用して、最適な次数を自動探索しましょう。
引数に d=1 と D=1 を設定することで、１階階差＆季節性１階階差を取るように指定できます。

### auto arima で最適なSARIMAのp,q,P,Qを探索

# 残差の検定
# Ljung-Box検定　：帰無仮説「自己相関関係はない」
# Jarque-Bera検定：帰無仮説「データは正規分布母集団から生成された」

sarima = auto_arima(train_df, seasonal=True, m=12, d=1, D=1)
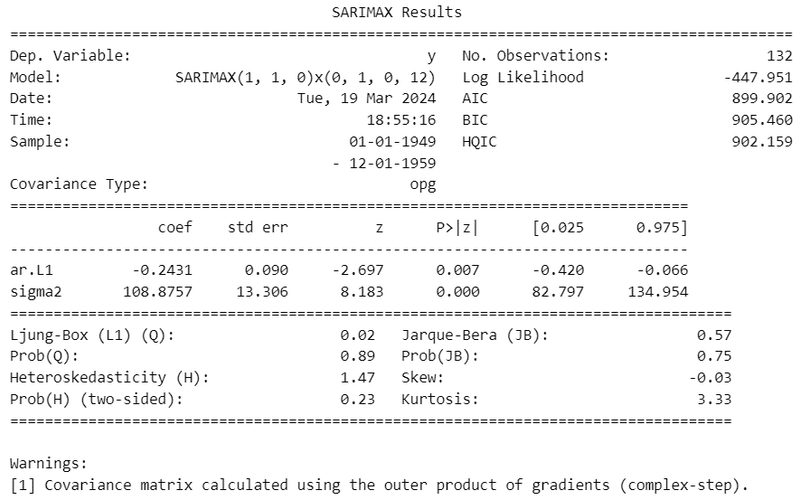
print(sarima.summary())

【実行結果】
最適モデルはSARIMA(1, 1, 0)(0, 1, 0, 12)モデルのようです。
「AR(1)過程, 1階階差、季節性1階階差、周期12」です。
MAは使わないようなので SARI モデルかもです。

■ 最適モデルの評価
残差が正規分布に従っているか、Jarque-Bera検定で確認しましょう。
上述の表の下段右「Prob(JB)」に注目します。
Jarque-Bera検定の$${p}$$値「Prob(JB)」の値は 0.75。
大きい値なので帰無仮説は棄却できず、帰無仮説どおり残差は「正規分布に従う」と解釈できそうです！
その他の指標では、Skew（歪度）の -0.03 は正規分布の歪度 0 に近似していて、Kurtosis（尖度）の 3.33 は正規分布の尖度 3 に近似しています。
残差が正規分布に従うという仮定は満たしているようです。

残差の自己相関の確認には Ljung-Box 検定を利用できます。
上述の表の下段左「Prob(Q)」に注目します。
Ljung-Box検定の$${p}$$値「Prob(Q)」の値は 0.89。
大きい値なので帰無仮説は棄却できず、帰無仮説どおり残差に「自己相関は無い」です！

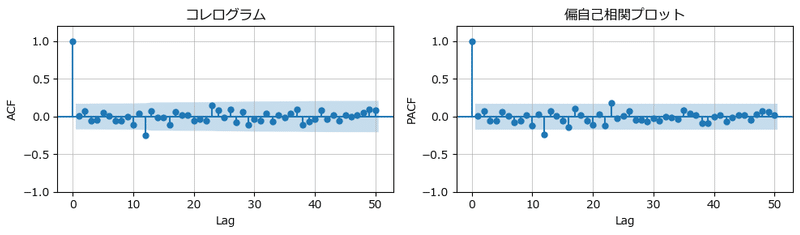
コレログラムと偏自己相関プロットで残差の自己相関の様子を確認しましょう。
テキスト図7-14に相当します。

### 図7-14 残差のコレログラムの描画

# 残差の取得
resid = sarima.resid()
# 描画領域の設定
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 3))
# コレログラムの描画
plot_acf(resid, lags=50, ax=ax1, title='コレログラム')
ax1.set(xlabel='Lag', ylabel='ACF', ylim=(-1, 1.2))
ax1.grid(lw=0.5)
# 偏自己相関プロットの描画
plot_pacf(resid, lags=50, ax=ax2, title='偏自己相関プロット')
ax2.set(xlabel='Lag', ylabel='PACF', ylim=(-1, 1.2))
ax2.grid(lw=0.5)
plt.tight_layout();

【実行結果】
青塗りの外側にはみ出た棒がほぼほぼ無いので、残差に自己相関無しです！

auto_arima で見つけた最適モデル「sarima」を使っていきましょう！

テスト期間の予測

「sarima」を「predict」することで将来期間の予測ができます。
今回は将来12ヶ月分を予測するので、引数 n_periods=12 とします。
ちなみに予測時に説明変数を与える必要は無いです。

### 将来24か月の予測
pred = sarima.predict(n_periods=12)
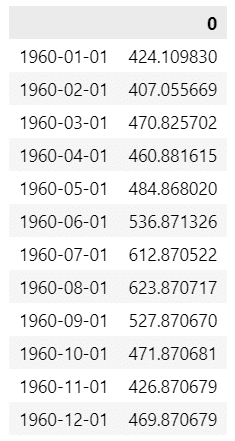
display(pred.to_frame().head())

【実行結果】
1960年の12か月分の予測値です。

1949～1960年の全期間について、観測値（正解値）と予測値を可視化しましょう。
テキスト図7-15に相当します。
学習期間の予測値は、最適モデル「sarima」に対して「fittedvalues()」を適用して取得できます。

### 観測値と予測値の時系列プロットの描画

# 描画領域の指定
fig, ax = plt.subplots(figsize=(10, 4))
# 観測値の折れ線グラフの描画
sns.lineplot(data=passengers, markers='o', ms=5, color='tab:blue', lw=0.8,
             legend=None, ax=ax)
# 予測値の折れ線グラフの描画
sns.lineplot(data=sarima.fittedvalues(), color='tab:orange', ls='--', ax=ax)
# 予測値の折れ線グラフの描画
sns.lineplot(data=pred, color='tab:red', ls='--', ax=ax)
# 予測期間の塗りつぶし等
ax.axvline(pd.to_datetime('1960-01-01'), color='black', ls='--', lw=0.5)
ax.axvline(pd.to_datetime('1960-12-01'), color='black', ls='--', lw=0.5)
ax.fill_between([pd.to_datetime('1960-01-01'), pd.to_datetime('1960-12-01')],
                0, 650, color='lightpink', alpha=0.2)
# 修飾
ax.set(xlabel='年月', ylabel='月間乗客者数[千人]', ylim=(0, 650),
       title='1949－1960年のアメリカ飛行機乗客数')
ax.grid(lw=0.5)
# 凡例
ax.plot([], [], '-o', ms=5, lw=0.8, color='tab:blue', label='観測値')
ax.plot([], [], color='tab:orange', ls='--', label='予測値:学習データ')
ax.plot([], [], color='tab:red', ls='--', label='予測値:テストデータ')
ax.legend();

【実行結果】
薄赤色面がテスト期間です。
青い観測値と赤点線の予測値は近い感じがします！

異常検知の実行

いよいよ大詰めです！

■ 異常度の算出
残差が正規分布に従う仮定が満たされる場合、異常度$${a(y_t^{\prime})}$$は次式で計算できます。

$${y_t}$$は時間$${t}$$における観測値、$${y_t^{\prime}}$$は$${y_t}$$に対する予測値、$${\sigma}$$は残差の標準偏差（正確には誤差の標準偏差）です。

テキストによるとARIMAモデルに関して上述の異常度を適用しています。
SARIMAモデルも同様に上述の異常度を使えるかどうかは分かっていません。
でも上述の異常度を使ってみます！

■ 異常度の閾値
残差が正規分布に従う仮定が満たされて説明変数が$${M}$$個のとき、異常度は自由度$${\boldsymbol{M}}$$のカイ二乗分布に従います。
今回の時系列データが説明変数が１つなので、閾値は自由度１のカイ二乗分布のたとえば 99%点（上側 1%点）や 95%点（上側 5%点）などを採用することになります。

■ 異常検知の実装
この記事では閾値を 99%点（上側 1%点） にします。
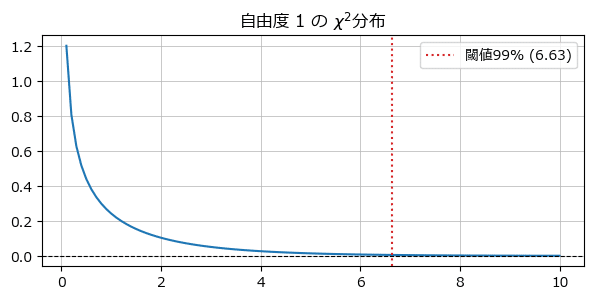
カイ二乗分布を確認してみましょう。

### 異常度の閾値に用いたカイ二乗分布の描画

## 設定
# 自由度（変数の数M）
df = 1
# 基準値
pp = 0.99

## カイ二乗分布の確率密度関数と閾値の算出
xval = np.linspace(0, 10, 101)
yval = stats.chi2.pdf(x=xval, df=df)
threshold = stats.chi2.ppf(q=pp, df=df)

## 描画
# 描画領域の設定
plt.figure(figsize=(7, 3))
# カイ二乗分布の確率密度関数の描画
sns.lineplot(x=xval, y=yval)
# 閾値の垂直線の描画
plt.axvline(threshold, color='tab:red', ls=':',
            label=f'閾値{pp:.0%} ({threshold:.2f})')
# y=0の水平線の描画
plt.axhline(0, color='black', lw=0.8, ls='--')
# 修飾
plt.title('自由度 1 の $\chi^2$分布')
plt.grid(lw=0.5)
plt.legend();

【実行結果】

テストデータの異常度の算出、異常度の閾値の算出、閾値を超えるデータ点の抽出を行います。
テキストにならって 99%点に加えて 95%点も算出します。

### 異常検知の実行

## 異常度aの算出
# 学習データの残差の標準偏差の算出
sigma = resid.std(ddof=0)
# テストデータの異常度aの算出 ((実績値-予測値) / 標準偏差)^2
a = ((test_df.value - pred) / sigma)**2

## 異常度の閾値の算出 自由度M=説明変数数のカイ二乗分布の95%点（または99%点）
thres99 = stats.chi2.ppf(q=0.99, df=1)
thres95 = stats.chi2.ppf(q=0.95, df=1)
thres88 = stats.chi2.ppf(q=0.88, df=1)

## 閾値を超える異常度の算出
a_99 = a[a > thres99]
a_95 = a[a > thres95]

## 結果表示
print(f'99%閾値: {thres99:.3f}')
print(f'99%閾値で異常値と判定:\n{a_99}')
print(f'\n95%閾値: {thres95:.3f}')
print(f'95%閾値で異常値と判定:\n{a_95}')

【実行結果】
99%閾値では1960年3月が異常だと判別されました。

異常度を可視化します。
テキスト図7-16に相当します。

### 異常度の散布図の描画

# 描画領域の設定
fig, ax = plt.subplots(figsize=(10, 4))
# 異常度aの散布図の描画
sns.scatterplot(x=test_df.index, y=a, s=80, ec='white', alpha=0.7, ax=ax)
# 閾値88%の水平線の描画
ax.axhline(thres88, color='tab:red', lw=0.9, ls='-.',
           label=f'88% ({thres88:.2f})')
# 閾値95%の水平線の描画
ax.axhline(thres95, color='tab:red', lw=0.9, ls='--',
           label=f'95% ({thres95:.2f})')
# 閾値99%の水平線の描画
ax.axhline(thres99, color='tab:red', lw=0.9, ls=':',
           label=f'99% ({thres99:.2f})')
# 修飾
ax.set(xlabel='年月', ylabel='異常度$a$', title='テストデータの異常度プロット')
ax.legend(title='閾値', loc='upper left')
ax.grid(lw=0.5);

【実行結果】
３つの閾値で異常度を可視化しました。
閾値を99%点に置くと異常データは１点、95%点に置くと異常データは３点になります。
閾値を88%にしても異常検知ができるかもしれません（あくまで想像上のつぶやき）。

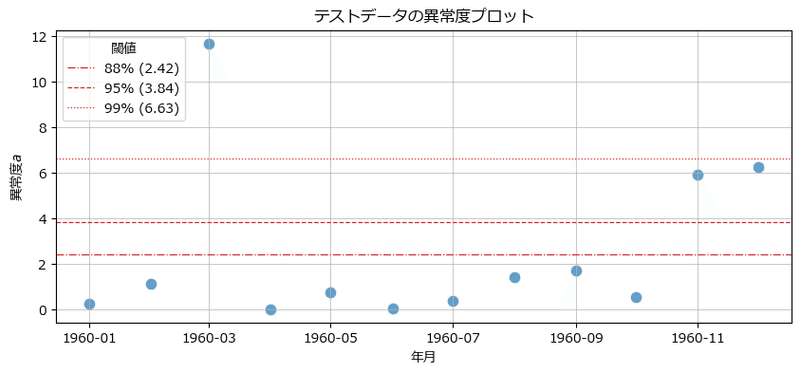
ところで、1960年3月、11月、12月は観測値が予測値よりも小さい値になっていることが気になります！
つまり、過大な予測をしている状態なのです。
この３つの月に乗客数を減少させるような事象が起きていたのでしょうか？
それとも、1960年は既に国際線が当たり前の時代になっていて、従来の高い乗客数伸び率（トレンド）が落ち着きつつある年なのでしょうか？
気になります・・・

第７章③の寄り道写経は以上です。

シリーズの記事

次の記事

前の記事

目次

ブログの紹介

note で７つのシリーズ記事を書いています。
ぜひ覗いていってくださいね！

１．のんびり統計

統計検定２級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定２級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。

２．実験！たのしいベイズモデリング１＆２をPyMC Ver.5で

書籍「たのしいベイズモデリング」・「たのしいベイズモデリング２」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは Ｒ言語＋Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう！

３．実験！岩波データサイエンス1のベイズモデリングをPyMC Ver.5で

書籍「実験！岩波データサイエンスvol.1」の４人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう！

４．楽しい写経 ベイズ・Python等

ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀

５．RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で

書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん！
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。

６．データサイエンスっぽいことを綴る

統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。

７．Python機械学習プログラミング実践記

書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。

最後までお読みいただきまして、ありがとうございました。