今回の統計トピック

今回から分散分析のテーマが始まります。
まずはシンプルな一元配置分散分析表を検討します。
分散分析特有の用語や記号遣いがあるので、徐々に慣れていきましょう！

公式問題集の準備

「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください！
「知る」「実践する」の章で、のんびり統計をお楽しみください！

今回の記事の構成

この記事は、通常の記事構成と違う章立てにいたします。
「問題を解く」と「知る」を１つの章にまとめます。
次に「実践する」で例題を用いて一元配置分散分析を手作業・EXCEL・R・Pythonで実践いたします。

問題を解きながら知る

📘公式問題集のカテゴリ

線形モデルの分野　～分散分析の分野
問1 一元配置分散分析の基本（地域別売上）

試験実施年月
調査中

📕公式テキスト：5.2.1 １元配置分散分析（185ページ～）

問題

公式問題集をご参照ください。

解き方

題意
問題文に記載された一元配置分散分析表に基づいて、次の３問を解答します。
① 分散分析表から量的変数の不偏分散を算出
② 分散分析表の穴埋め
③ 分散分析表に基づく統計的仮説検定の結論

問題の趣旨をざっくり洗ったのちに、分散分析の概要を確認しましょう。

■ 関心のあること
「各地域の売上に違いがあるのか知りたい」
本問題が最も関心を示していることです。
一元配置分散分析を用いて「売上平均が他地域と異なる地域があるかどうか」を検定しましょう！

問題文から、地域は４つあり、各地域には５店舗あるので、合計２０店舗を運営しています。
地域・店舗・売上の値は次のような図の関係にあります。

■ 売上データのイメージ
問題文では明らかにされていませんが、分散分析表に用いた「観測データ」はきっと次のような形式でしょう。
青字は数値の想定です。

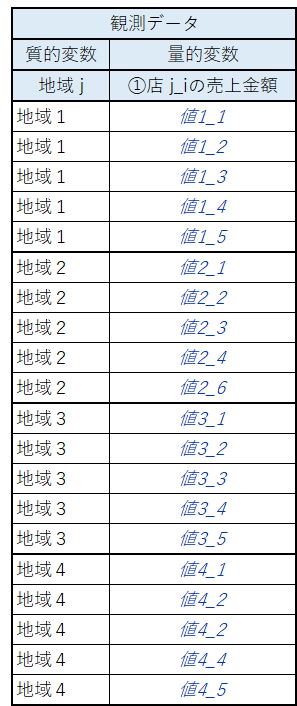
４つの地域は「質的変数」、店舗別の売上金額は「量的変数」です。
質的変数のカテゴリは「地域１」から「地域４」までの４つがあります。

分散分析では、質的変数のことを「要因」や「因子」と呼びます
本問題の要因は「地域」です。
また、質的変数のカテゴリ（グループ）のことを「水準」と呼びます。
本問題の水準は「地域１」から「地域４」までの４つの地域を指します。

一元配置分散分析は、質的変数１つと量的変数１つを使って、質的変数に含む水準（カテゴリ）と量的変数の関係を分析をします。

■ 分散分析表の役割
分散分析表は、地域１から地域４までの４つの水準の母平均に違いがあるかどうかを統計的仮説検定で結論づけるときに使用されます。
問題文の穴開きの分散分析表を再掲しましょう。

分散分析表の形式では「要因」欄に１つ「地域」が記載されます。
１つ下には「残差」が記載されています。
売上データ（観測データ）の細かなデータがどのように分散分析表にまとまっていくのでしょう？

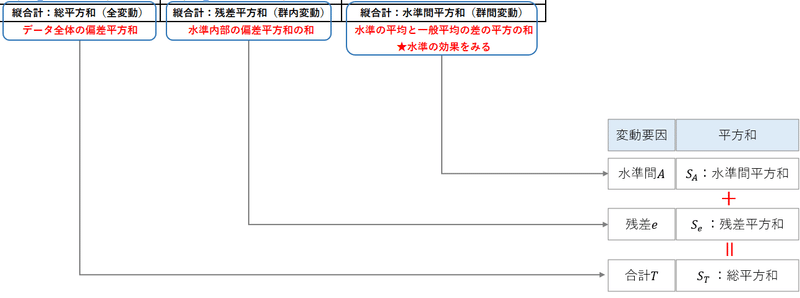
■ 平方和の計算メカニズム
まず、観測データと「地域の平均値」・「全データの平均値」を対応させます。
「全データの平均値」のことを一般平均と呼びます。
青字は店舗別の値、緑字は地域別の値、赤字は全店同一値です。

対応する２種類の平均値を用いて「平方和」を計算します。

非常に細かいですが、行単位・列単位で次の計算を行います。

関心事を思い出しましょう。
「各地域の売上に違いがあるのか知りたい」
これは「水準間平方和」に現れます。
水準間平方和は地域別の平均と一般平均（全体平均）の差を取り扱います。

もしも地域別の売上平均が同じであったら、水準間平方和はゼロになります。
なぜなら「地域別の売上平均が同じ＝地域別の売上平均は全体平均と同じ」ということになるからです。
分散分析表界隈で「水準」と呼ばれる４つの地域の売上平均の格差が大きいほど、水準間平方和の値も大きくなります。

■ 平方和から分散分析表へ
３つの平方和は、分散分析表の左に位置する「平方和」の部分に記載されます。

■ 分散分析表の顔つき
分散分析表のフォーム全体を見ましょう。
左には先程の計算シートから連動した「平方和」があります。
行には平方和に対応する「水準間」「残差」「合計」があります。

新しい項目は「自由度」「平均平方」「Ｆ値」「ｐ値」です。
自由度は、地域の数である「水準の数$${a=4}$$」と全店舗数である「標本サイズ$${n=20}$$」を用いて計算できます。
平均平方はずばり「分散」です。分散分析表の分散です。
Ｆ値は分散の比です。Ｆ比とも言います。

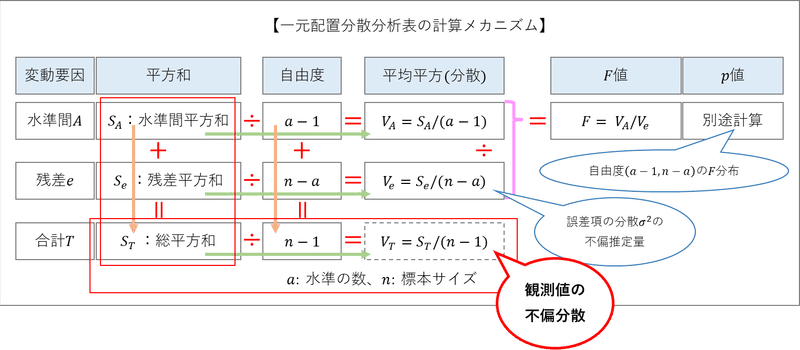
■ 分散分析表の計算メカニズム
この表は「平方和」と「自由度」が埋まれば、残りの項目のほとんどは一定のメカニズムで計算できます。
計算メカニズムを追いましょう。
赤い記号と色付きの線をご覧ください。

分散にはトピックがあります。
・残差の平均平方（分散）は誤差項の不偏分散です。
・合計の平均平方（分散）は観測値の不偏分散です。
また、Ｆ値は自由度$${(a-1, n-a)}$$の$${F}$$分布に従います。
ｐ値は、Ｆ値と$${F}$$分布から求めます。

計算メカニズムのマップが完成しました。

■ 分散分析表から統計的仮説検定へ
関心事「各地域の売上に違いがあるのか知りたい」は統計的仮説検定で調べます。
「違い」のことを水準の「効果」と呼びます。
特定の地域に売上を稼ぐパワーがあって、他の地域よりも売上が多い＝売上に違いがあるのは、その地域の効果なのです。

統計的仮説検定は「分散分析表で求めたＦ値・ｐ値」に基づいて判定をします。
帰無仮説は「すべての水準の効果は０である」または「すべての水準の母平均は等しい」です。
ｐ値が有意水準よりも小さい場合、帰無仮説は棄却され、いずれかの水準に効果がある、いずれかの水準の母平均は他と違う、と言う結論になります。

なお、$${F}$$分布上の棄却域に基づいて検定を行う場合、上側確率を利用する片側検定となります。

■ 統計的仮説検定、そういえば
統計的仮説検定の中にはよく似たものがあります。
「２標本の母平均の差の検定（$${t}$$検定）」です。
この検定は「２つの標本＝２つの水準」を取り扱います。
一方で、分散分析表は「３つ以上の水準の母平均の差」を取り扱うことができます。

■ 用語・記号のまとめ
分散分析の役者をまとめました。

さて、前置きはこれくらいにして、問題に戻りましょう。
（ヒントを手に入れましたか？？？）

① 分散分析表から量的変数の不偏分散を算出

全店売上の標本分散（不偏分散）を計算します。
分散分析表の計算メカニズムを思い出しましょう。

赤い吹き出しが指し示す箇所が「全データの不偏分散」の項目です。
「総平方和$${S_T}$$÷自由度$${n-1}$$＝観測値の不偏分散$${V_T}$$」です。
穴開きの分散分析表を見ましょう。

$${S_{T}}$$：総平方和は地域の平方和$${0.2204}$$と残差平方和$${0.3370}$$の和$${0.5574}$$です。
自由度$${n-1}$$は、データの数：標本サイズ$${n=20}$$ですので、$${20-1=19}$$です。
総平方和$${0.5574}$$を自由度$${19}$$で割ると、$${0.0293\cdots}$$です。

この問題の解答選択肢は ① 0.0293 です。

② 分散分析表の穴埋め

問題を確認しましょう。
５箇所のカッコ内の値を計算します。

分散分析表の計算メカニズムに沿って、カッコの数値を埋めましょう。
赤い太枠が計算対象の項目です。

■ 自由度

地域：水準の自由度は$${a-1}$$です。
水準の数$${a=4}$$ですので、$${a-1=4-1=3}$$です。
残差の自由度は$${n-a}$$です。
標本サイズ$${n=20}$$、水準の数$${a=4}$$ですので、$${n-a=20-4=16}$$です。
検算しましょう。
水準の自由度$${3+}$$残差の自由度$${16=}$$全体の自由度$${19}$$です。

■ 平均平方
地域：水準の平均平方は、水準間平方和／水準間の自由度です。
$${0.2204/3 \fallingdotseq 0.07347}$$です。
残差の平均平方は、残差平方和／残差の自由度です。
$${0.3370/16 \fallingdotseq 0.02106}$$です。

■ Ｆ値

Ｆ値は、水準間平均平方／残差平均平方です。
$${0.07347/0.02106 \fallingdotseq 3.488}$$です。

解答をまとめます。
（ア）から順に、$${3, 16,\ 0.07347,\ 0.02106,\ 3.488}$$です。 

この問題の解答選択肢は ⑤ です。

③ 分散分析表に基づく統計的仮説検定の結論

穴開きの分散分析表をみます。

この分散分析表に基づいて「有意水準$${5\%}$$」で検定を行って、帰無仮説、帰無仮説の棄却の有無、対立仮説を解答します。

まず帰無仮説と対立仮説です。
統計的仮説検定のまとめ資料を思い出します。

この問題は「検定の視点２」方式ですので、仮説は次のとおりです。
・帰無仮説は「全ての水準の母平均は等しい」
・対立仮説は「どれかの水準の母平均は異なる」

また、穴開きの分散分析表より、$${p}$$値は$${0.0405}$$です。
この$${p}$$値は有意水準$${5\%}$$を下回っているので、帰無仮説を棄却できます。

文章をまとめると次のようになります。

この問題の解答選択肢は ① です。

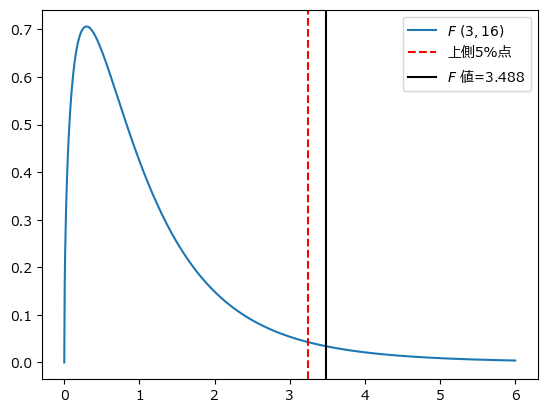
最後に自由度$${(3,16)}$$の$${F}$$分布の確率密度関数、上側$${5\%}$$、$${F}$$値$${3.488}$$の関係をグラフで確認しましょう。

解答

〔1〕①、〔2〕⑤、〔3〕① です。

難易度　やさしい

・知識：標本不偏分散、一元配置分散分析表、分散分析による母平均の差の検定
・計算力：数式組み立て（低）、電卓（低）
・時間目安：3問合計 5分

実践する

例題を解いて一元配置分散分析を実践する

例題の一元配置分散分析を手作業、EXCEL、R、Pythonで実践しましょう！

例題
お友だちに３種類のどうぶつの好感度を訊きました。
「とら」「くま」「うま」です。
好感度は０～１０です。
値の大きさが好感度の高さを示します。

訊いた結果を表にまとめました。
さて、どうぶつの好感度に差はあるのでしょうか？

CSVファイルのダウンロード
こちらのリンクから「どうぶつ好感度データ」のCSVファイルをダウンロードできます。
R、Python で CSV ファイルを利用します。

さあ、一元配置分散分析で検定しましょう！
有意水準を$${\boldsymbol{5\%}}$$とします。
レッツゴー！

手作業で作成してみよう！

① 平方和の算出

さっそく「平方和の計算メカニズム」表を埋めていきます！
まず左側のゾーンです。
青い項目は、どうぶつ好感度データを「質的変数」と「量的変数」に区分して整理し直しました。
ピンクの項目は、②がどうぶつ別平均です。
とらの平均、くまの平均、うまの平均です
③は、とら～うまの全てのデータの平均です。

好感度データと平均値を埋めたところで、右側のゾーンに計算を進めます。

黄色の項目が増えました。
④は「（①好感度－③全平均）の２乗」の数値です。
⑤は「（①好感度－②どうぶつ別平均）の２乗」の数値です。
⑥は「（②どうぶつ別平均－③全平均）の２乗」の数値です。

④～⑥の縦合計が平方和のゴールです。
左から「総平方和」「残差平方和」「水準間平方和」です。
この３つの平方和を「分散分析表」に持ち込みます！

② 分散分析表の計算

いかがでしょう？
「どうぶつ」の「平方和」は水準間平方和です。

要因「どうぶつ」と「残差」の横に向かって「平方和÷自由度＝平均平方」を計算しましょう。
最後に「どうぶつの平均平方÷残差の平均平方＝F値」を計算しましょう。

さて、p値はどうやって計算するのでしょう・・・
（Excelの関数を使いました）

③ 統計的仮説検定の結論

どうぶつの好感度に差はあるかを知りたいのでした。
帰無仮説は「どうぶつの好感度の母平均は等しい」です。
$${p}$$値の計算が煩雑なことを踏まえて、$${F}$$分布のパーセント点を用いて棄却域を算出しましょう。

検定の方法は「上側確率」の片側検定です。
有意水準は$${5\%}$$に設定しました。
自由度$${(2,12)}$$の上側$${5\%}$$点を取得して、$${F}$$値と比べることにしましょう。

第２自由度の欄に「12」が無いので、代用として「15」を利用します。
かなりザックリしていますのでご容赦くださいな🌺

自由度$${(2,15)}$$の上側$${5\%}$$点は$${4.103}$$です。
$${F}$$値$${5.340}$$は上側$${5\%}$$点$${4.103}$$よりも大きいので、棄却域に含まれます。

【結論】
有意水準$${\boldsymbol{5\%}}$$で帰無仮説は棄却され、対立仮説「どうぶつのどれかの母平均は他のどうぶつと異なる」と言えます。

自由度$${(2,15)}$$の$${F}$$分布で上側$${5\%}$$点と$${F}$$値の位置関係を確かめましょう。

確かに、$${F}$$値（黒線）は上側$${5\%}$$点（赤点線）の上側、つまり棄却域に位置しています。

■ 信頼区間の可視化

「とら」「くま」「うま」の好感度の$${95\%}$$信頼区間を可視化しましょう。

$${95\%}$$信頼区間の公式は次のとおりです。

計算しましょう。
実はこのデータは、各水準の標本サイズ$${n_j}$$は全て$${5}$$で等しいです。
なので、$${t_{\alpha/2}(n-a)\sqrt{V_e/n_j}}$$は１つの値になります。
まずは、$${t_{\alpha/2}(n-a)\sqrt{V_e/n_j}}$$を計算しましょう。

① $${t}$$分布のパーセント点$${t_{\alpha/2}(n-a)}$$

信頼区間$${95\%}$$の場合、$${\alpha}$$は$${1-0.95=0.05}$$です。
したがって、$${\alpha/2}$$は$${0.025}$$です。
また、残差の自由度$${n-a}$$は、$${15-3=12}$$です。
まとめますと、自由度$${12}$$の$${t}$$分布の$${2.5\%}$$点を見つけましょう。

$${t_{\alpha/2}(n-a)}$$は$${2.179}$$です。

② $${t_{\alpha/2}(n-a)\sqrt{V_e/n_j}}$$の計算

$${t_{\alpha/2}(n-a)=2.179}$$、残差の平均平方$${V_e=3.2333}$$、各水準の標本サイズ$${n_j=5}$$を用いて計算すると、$${1.75}$$です。

③ 各水準の平均値$${\bar{y}_j}$$

各どうぶつの平均値を求めます。

④ 各水準の信頼区間
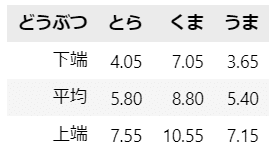
各水準の平均値$${\bar{y}_j \pm 1.75}$$が信頼区間です。

信頼区間の下端・上端の値を計算して表にしました。

答えが出揃ったところで、グラフにしましょう。
中央の青丸は平均値、上下に伸びるヒゲの区間が「各どうぶつの好感度の母平均の$${95\%}$$信頼区間」です。

実は分散分析では、どのどうぶつの母平均が異なるのか判明しません。
どうぶつ毎の信頼区間の可視化によって、平均値が異なるどうぶつを想像することはできそうです。（🧸？）

母平均が異なるどうぶつをPythonで確認したいと思っています。

EXCELで作成してみよう！

２種類の方法で一元配置分散分析表を作成しましょう。
・EXCEL関数を活用
・データ分析機能の「分散分析－一元配置」

好感度データは、予め、どうぶつ単位で列を分けておきます。

Ⅰ．EXCEL関数を活用

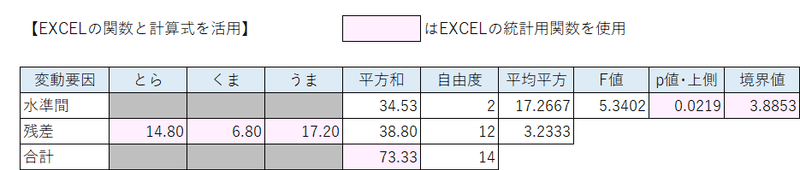
完成イメージは次のようになります。

ピンク色のセルで統計関係のEXCEL関数を用いています。

はじめに、各水準（どうぶつ単位）の残差を計算します。
「とら」を例にして確認しましょう。

■ 利用関数：DEVSQ 関数
「偏差平方和」の計算ができます。
「とら」の好感度を範囲指定しています。
範囲内の値で平均値を算出して、各値と平均値の差を二乗して、合計しています。

次に、合計の平方和を計算します。
こちらも「DEVSQ 関数」で、全ての好感度の値の偏差平方和を計算します。

続いて、ｐ値を計算します。
Ｆ値と自由度を用いて、$${F}$$分布の上側確率を計算します。

■ 利用関数：F.DIST.RT 関数
Ｆ値について、自由度（水準間自由度、残差自由度）の$${F}$$分布の上側確率を算出します。
引数に ( Ｆ値, 水準間自由度, 残差自由度 ) を指定します。

最後に、境界値を計算します。
境界値は、棄却域の境界となる「棄却限界値」のことです。

■ 利用関数：F.INV.RT 関数
有意水準$${5\%}$$について、自由度（水準間自由度、残差自由度）の$${F}$$分布の上側％点を算出します。
引数に ( 有意水準, 水準間自由度, 残差自由度 ) を指定します。

さあ、もう一度、分散分析表の完成イメージを確認しましょう。

統計的仮説検定の結論を出すときが来ました。
$${p}$$値が有意水準$${5\%}$$より小さい、または、Ｆ値が境界値より大きいので、有意水準$${5\%}$$で帰無仮説は棄却されます。

Ⅱ．データ分析機能の「分散分析－一元配置」

完成イメージは次のようになります。
各水準（どうぶつ単位）の要約統計量が併記されるので、データの読み取りがしやすいです！
好感度の平均値は「くま」がダントツです。

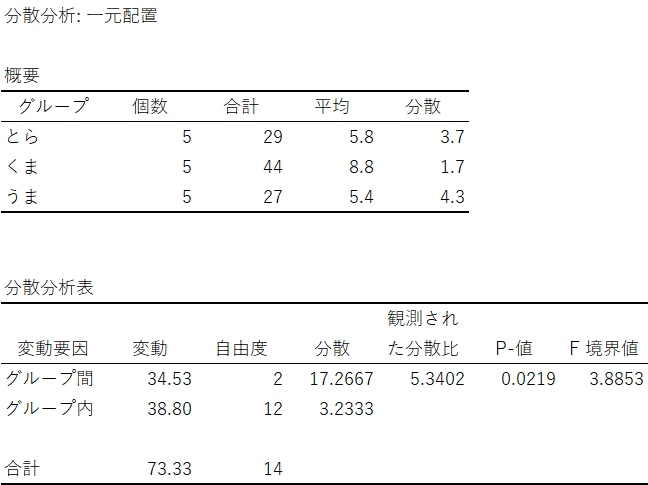
先に結論しましょう。
P-値が有意水準$${5\%}$$より小さい、または、Ｆ値（観測された分散比）がＦ境界値より大きいので、有意水準$${5\%}$$で帰無仮説は棄却されます。

■ 作成方法
メニューより、データ　＞　データ分析　を指定して、「データ分析」画面を開きます。

「データ分析」画面で「分散分析：一元配置」を選んで「ＯＫ」ボタンをクリックします。

「分散分析：一元配置」画面が表示されます。

入力範囲等を指定して「ＯＫ」ボタンをクリックすると、出力先に分散分析表が表示されます。

かなりシンプルな操作で本格的な分散分析表を作成できます。
ぜひぜひ、３種類以上のグループのデータ平均を比べてみましょう！

EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。

R で作成してみよう！

R スクリプトで一元配置分散分析を実践します。
コードはめっちゃシンプルです。

① データの読み込み

### データの読み込み
data <- read.csv('sampledata.csv')
# データの要約表示
str(data)
summary(data)

【出力結果】
データは変数「どうぶつ」と変数「好感度」で構成されます。

② どうぶつ別の統計量の表示
psych ライブラリの describeBy 関数を利用します。

### どうぶつ別の統計量
library(psych)
describeBy(data$好感度, data$どうぶつ)

【出力結果】
かなり詳細に要約統計量を表示してくれました。

③ 箱ひげ図の描画
箱ひげ図でどうぶつ毎のデータの外観を確認しましょう。

### 箱ひげ図グラフ
boxplot(好感度~どうぶつ, data=data, main='どうぶつの好感度', 
        col=c('lightpink', 'lightgreen', 'lightblue'))

【出力結果】
くまのダントツで好感度が高いです。

④ 分散分析の実行
真打ちの登場です。
たった１行で分散分析ができます！

### 分散分析の実施と結果表示
anova(aov(好感度 ~ どうぶつ, data=data))

【処理結果】
$${p}$$値の表示があるので、検定の結論を出しやすいです。

R のコードは非常にシンプルです。
シンプル・イズ・ベストな方にお勧めいたします。

Rサンプルファイルのダウンロード
こちらのリンクからRスクリプト形式のサンプルファイルをダウンロードできます。

Pythonで作成してみよう！

３つのライブラリで一元配置分散分析を実施します。
最後に、多重比較の方法を用いて、母平均が異なるどうぶつを検討します。

① インポート

### インポート

# 数値計算
import numpy as np
import pandas as pd

# 統計処理
from scipy import stats
import statsmodels.api as sm
import statsmodels.formula.api as smf
import pingouin as pg

# 可視化
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'

② データの読み込み

### データの読み込み
data = pd.read_csv(r'sampledata.csv')
print('data.shape', data.shape)
display(data)

【出力結果】

③ どうぶつ別の要約統計量
pandas の ピボットテーブル関数を用いて、どうぶつ別の要約統計量をデータフレーム形式で作成します。
aggfunc 引数で統計量を指定します。

data.pivot_table(index=None, columns='どうぶつ', values='好感度',
                 aggfunc={'好感度': [len, np.sum, np.mean, np.std, min,
                                     np.median, max]},
                 sort=False).round(3)

【出力結果】

④ 箱ひげ図の描画
seaborn の boxplot を利用します。

### 箱ひげ図の描画
sns.boxplot(x='どうぶつ', y='好感度', data=data);

【出力結果】

⑤ 分散分析の実行
statsmodels、scipy.stats、pingouin の分散分析を比べてみましょう。

■ statsmodels
回帰分析と同じように、ols（最小二乗法）に fit させてから、「anova_lm」で分散分析を実行します。

### 分散分析 statsmodels
# df:自由度、sum_sq:平方和、mean_sq:平均平方、F:F値、PR(>F):上側片側確率のp値

# モデルの定義・フィット
anova = smf.ols('好感度 ~ どうぶつ', data=data).fit()
# 分散分析の実行
result_sm = sm.stats.anova_lm(anova, typ=1)
result_sm.round(4)

【出力結果】
一元配置分散分析表の「水準間」「残差」（Residual）行が表示されます。
R の出力結果と同じレベルです。

■ scipy.stats
一元配置分散分析用の関数 f_oneway を利用します。
この関数は、引数に「水準別」（どうぶつ別）に分けられたデータを指定する必要があります。
そこで、コードの前段で、水準別データを作成しています。
pandas の groupby を使って、どうぶつ別データを作成しました。
変数名に「ひらがな」を使ってみました（かわいい）。

### 分散分析 scipy.stats

# GroupByオブジェクトの生成
animal_g = data.groupby('どうぶつ', sort=False)

# 水準別データの作成
とら = animal_g.get_group('とら')['好感度']
くま = animal_g.get_group('くま')['好感度']
うま = animal_g.get_group('うま')['好感度']

# 分析分析の実行＆データフレームに格納
result_stats = pd.DataFrame(columns=['F値', 'p値'])
result_stats.loc['どうぶつ'] = stats.f_oneway(とら, くま, うま)
result_stats.round(4)

【出力結果】
f_oneway 関数の出力は$${F}$$値と$${p}$$値の２項目です。
分散分析表、とまでは行かないようですね。

■ pingouin
ダークホース的存在のpingouin。
anova 関数で分散分析を行います。
引数は、dv:目的変数（従属変数）、between:水準を含む変数（水準間）などです。
statsmodels のような事前の最小二乗法処理が不要であり、なかなか使い勝手が良さそうです。

### 分散分析 pingouin
## Source:要因、SS:平方和、DF:自由度、MS:平均平方、F:F値、P-unc:p値、np2：相関比

result_pg = pg.anova(dv='好感度', between='どうぶつ', data=data, detailed=True)
result_pg.round(4)

【出力結果】
一元配置分散分析の「水準間」「残差」（水準内：Within）行が表示されました。
分散分析表の項目が網羅されています。
そして、相関比$${\eta^2}$$（np2）の表示もあります。
相関比は、質的変数と量的変数の相関関係にかかわる統計量です。
「水準間平方和÷総平方和」で計算できます。

⑥ 各水準の信頼区間の描画
記事に用いた信頼区間のグラフを描画します。
思いの外、長いコードになりました。

■ 計算要素の算出

### 信頼区間の計算要素の算出

# 設定 信頼係数
cf = 0.95

# 計算要素の算出
df = result_sm.df.Residual                     # 残差の自由度
mean_square = result_sm.mean_sq.Residual       # 残差の平均平方
t_ppf = stats.t.ppf((1 + cf) / 2, df)          # t分布の上側cf/2％点
counts = animal_g.count()                      # 各水準のデータ数
means = animal_g.mean()                        # 各水準の平均値

# 信頼区間の片幅（正値側）の算出
ci_upper = t_ppf * np.sqrt(mean_square / counts)

# 計算要素の表示
print(f't分布の上側{(1-cf)/2:.1%}: {t_ppf:.3f}, 残差の平均平方: {mean_square:.3f}, '
      f'信頼区間の片幅（正値側）: {ci_upper.iloc[0, 0]:.3f}')

【出力結果】

■ 信頼区間の表示
pandas のデータフレーム形式に加工するので、コードが増えました。

### どうぶつ別の信頼区間の表示

# 下端の設定
animal_ci = (means - ci_upper).rename(columns={'好感度': '下端'})
# 平均の設定
animal_ci['平均'] = means
# 上端の設定
animal_ci['上端'] = means + ci_upper
# 表示
animal_ci.T.round(2)

【出力結果】

■ グラフ描画
matplotlib の errorbar 関数を利用します。
信頼区間の片側の値を引数「yerr」に渡します。

### エラーバー付きプロットの描画

# エラーバー付きプロットの描画
plt.errorbar(means.index, means['好感度'], yerr=ci_upper['好感度'],
             marker='o', markersize=15, linewidth=0, elinewidth=1,
             ecolor='gray', capsize=10)
# 修飾
plt.xlim(-1 ,3)
plt.ylim(0, 11)
plt.title('どうぶつの好感度 母平均の95%信頼区間')
plt.ylabel('好感度')
plt.show()

【出力結果】

⑦ 多重比較
どのどうぶつの母平均が異なるかをチェックしましょう。
その前に、どうぶつ好感度データが正規性・等分散性を満たすかどうか、検定します。

■ 正規性・等分散性の検定のための関数

### 検定の結果を返す関数
def test_result(test_func, term):
    # 有意水準の設定
    alpha = 0.05
    # p値の取得
    x = test_func
    # p値が有意水準以上の場合、帰無仮説は棄却されず、正規性／等分散性ありと判定する
    if x >= alpha:
        return f'p値={x:.4f}  {term}あり'
    else:
        return f'p値={x:.4f}'

■ 正規性の検定～Shapiro-Wilk検定
scipy.stats の shapiro 関数を用いて、Shapiro-Wilk検定を実行します。
戻り値は、統計値と$${p}$$値です。
３つのどうぶつの好感度は、それぞれ正規性ありです。

#### 正規性の検定～Shapiro-Wilk検定
# 帰無仮説「データは正規分布に従う」：有意水準5%で棄却されないので正規性ありと解釈
print(f'とら: {test_result(stats.shapiro(とら)[1], "正規性")}')
print(f'くま: {test_result(stats.shapiro(くま)[1], "正規性")}')
print(f'うま: {test_result(stats.shapiro(うま)[1], "正規性")}')

【出力結果】

■ 等分散性の検定～Bartlett検定
scipy.stats の bartlett関数を用いて、Bartlett検定を実行します。
戻り値は、統計値と$${p}$$値です。
３つのどうぶつの好感度の分散は等しい（等分散性あり）です。

### 等分散性の検定～Bartlett検定
# 帰無仮説「各群の分散は等しい」：有意水準5%で棄却されないので「等しい」と解釈
print(f'{test_result(stats.bartlett(とら, くま, うま)[1], "等分散性")}')

【出力結果】

■ 多重比較検定の実行
正規性・等分散性ともに「あり」なので、多重比較をTukey検定で行います。
３つのどうぶつの全組み合わせについて、母平均に違いがあるかどうかを検定します。
statsmodels の pairwise_tukeyhsd 関数を利用します。

### インポート
from statsmodels.stats.multicomp import pairwise_tukeyhsd

### 多重比較～Tukey検定
print(pairwise_tukeyhsd(data['好感度'], data['どうぶつ'], alpha=0.05))

【出力結果】
右端の reject（棄却）を見ましょう。
「True=棄却される」の組み合わせは「うま」「くま」です。
「うま」・「くま」の組み合わせは、有意水準$${\boldsymbol{5\%}}$$で「母平均に差があり」と結論できます。
ちなみに「くま」「とら」の組み合わせは、差があるとは言えない、という結論になりました。

Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。

おわりに

分散分析のテーマが始まりました。
質的変数と量的変数の組み合わせを対象にした統計的仮説検定です。
「質的変数のカテゴリごと」の「量的変数の平均値」に差があるかをみます。
独特の用語・記号・数式が出てきますが、手を動かして計算メカニズムに慣れると、一元配置分散分析の実践が楽しくなると思います。

最後までお読みいただきまして、ありがとうございました。

のんびり統計シリーズの記事

次の記事

前の記事

目次