計算機に少し詳しい方は、計算結果が周期的になったり、そうでなかったりするのは計算誤差のせいではないか、と考えるかもしれません。実際、ローレンツの場合も、上田睆亮の場合も、当初はそのような批判があったようです。1974年にロジスティック写像について研究していたRobert May教授もカオス状態になるのは計算誤差によるものと推測していたくらいです。
　計算機で誤差、というと、１÷３の計算を思い浮かべるかもしれません。電卓で 1÷3を計算したのち、その結果に3を掛けると 0.99999999となって１に戻りません。8桁電卓の場合、表示を8桁で打ち切ってしまうからです。しかし，MacOSやWindowsに付属している電卓アプリではちゃんと１に戻ります。どうなっているのでしょうか。結構複雑です。
　Excelは小数計算が苦手、というのは実は有名な話で、知っている人も多いと思います。たとえば、A1セルに −5 、A2セルに−4.9 をいれておいて、オートフィルでA列に0.1刻みの表を作ったとき、A51セルは０になりません。-2と -1.9から始めると0になります。-3と-2.9ではどうでしょうか。やってみてください。ただし，Excelも改訂されているので結果が異なるかもしれません。

　そこで、ロジスティック写像を例に、計算誤差について検証してみましょう。ロジスティック写像の式と、それを展開した式ではかけ算の回数が違います。そのために計算誤差が発生するというものです。ロジスティック写像の２つの式とは次の式です。

　　　$${x_{n+1}=ax_n(1-x_n)}$$
　　　$${x_{n+1}=ax_n-ax_n x_n}$$

この2式に対して，表計算ソフトや数式処理ソフト，プログラミング言語で結果を比較します。

表計算ソフトによる誤差

　いま，$${a=3.9}$$ とし，初期値を0.5 とします。
A1セルとB1に初期値の0.5を入れます。
A2セルには計算式の =3.9A1(1-A1) を，B2セルには =3.9B1-3.9B1*B1 を入れて，ずっと下の方にコピーしていきます。
　筆者はWindowsのExcelを持っていませんので，互換ソフトのWPS Office を使いました。その結果，39行目から結果が違っています。数年前のExcelでは25行目ですでに違っていました。今のExcelではどうでしょうか。

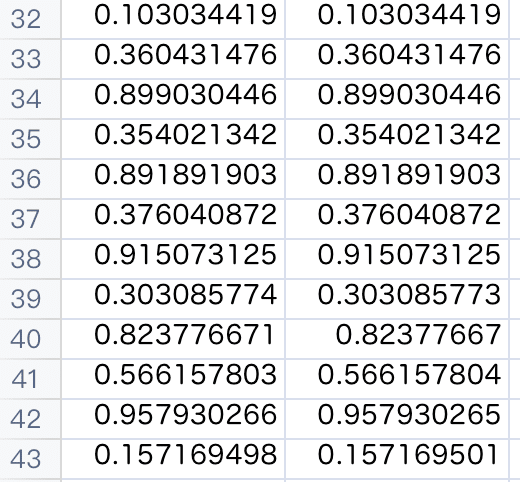
　さらに興味深い結果を示しましょう。ひとつは，セルの書式設定で小数点以下の表示を16位までに増やすこと，もう一つは，２つの計算式による結果が等しいかどうかを，IF 文を使って判定させることです。C列に，「=IF(A2=B2,1,0)」を入れます。「A2とB2が等しければ 1，そうでなければ 0」ということです。すると，次のような結果になりました。

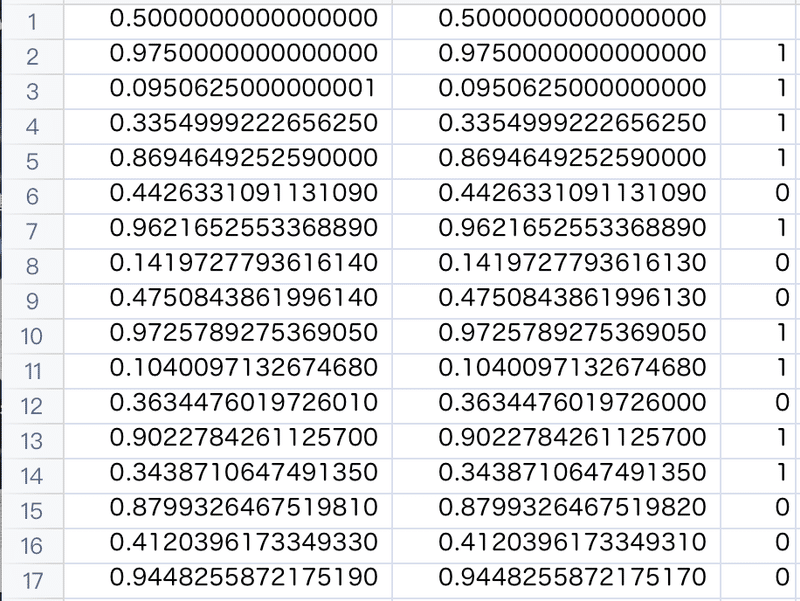
A列とB列を目視で比較すると，8行目で異なる結果になっています。C列で比較結果を見ると，6行目が0なので，ここで異なることになりますが，次の7行目では同じ，ということを示しています。奇妙ですね。
　しかし，これが表計算ソフトの計算誤差による結果なのです。

　次に数式処理ソフト用いて繰り返し計算を行い，その結果を折れ線グラフにして表示します。北海道大学大学院の井上純一氏の講義ノートから，第２回の「数値計算上の丸め誤差による影響」を参考にしました。なお，講義ノートはWeb上に公開されていましたが現在は削除されています。

数式処理ソフトによる誤差

　数式処理ソフトの代表格であるMathematica でやってみました。Mathematica は無料ではないので追試はしにくいかもしれませんが，参考まで。
コードは次の通り。

a = 3.9;
x1 = 0.5;
x2 = 0.5;
p1 = {{0, x1}};
p2 = {{0, x2}};
p3 = {{0, x1, x2}};
f1[x_] := ax(1 - x);
f2[x_] := ax - ax*x;
For[i = 0, i < 80, i++,
    xx1 = f1[x1];
    xx2 = f2[x2];
    p1 = Append[p1, {i/80, xx1}];
    p2 = Append[p2, {i/80, xx2}];
    p3 = Append[p3, {i + 1, xx1, xx2}];
    x1 = xx1;
    x2 = xx2;
];
g1 = ListLinePlot[p1, PlotStyle -> RGBColor[1, 0, 0]];
g2 = ListLinePlot[p2, PlotStyle -> RGBColor[0, 0, 1]];
Show[g1, g2]
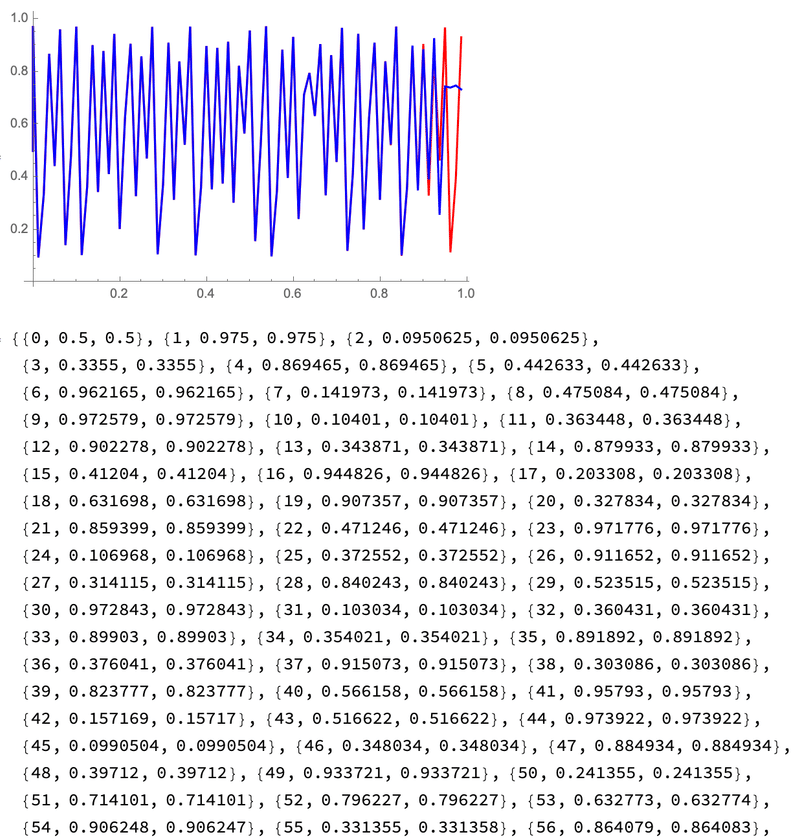
p3

x1,x2 は２つの計算式で算出した値。p1,p2 は折れ線グラフにするための点のリスト，p3 は2つの値を比較して表示するためのリストです。$${x_{n+1}=ax_n(1-x_n)}$$ による点列を ListLinePlot[・・]で赤の線分で結び，$${x_{n+1}=ax_n-ax_n x_n}$$ による点列を青の線分で結んで折れ線グラフにします。
実行結果は次の通り。値を比較すると 53 回目に異なる値になっています。

プログラミング言語による誤差

　このnoteでのカオスの記事の図は，数学ソフトのCinderella に付属しているプログラミング言語を使って描いています。そこで，CindyScript でプログラムを書いてみます。モジュールなどの import は不要で，簡単にプログラムが書けます。
コードは次の通り。

a = 3.9;
x1 = 0.5;
x2 = 0.5;
f(x):= a*x*(1 - x);
g(x):= a*x - a*x*x;
repeat(80,n,
  xx1 = f(x1);
  xx2 = g(x2);
  draw([[(n-1)/5, x1*10], [n/5, xx1*10]], size->1, color->[1, 0, 0]);
  draw([[(n-1)/5, x2*10], [n/5, xx2*10]], size->1, color->[0, 0, 1]);
  x1 = xx1;
  x2 = xx2;
  println(n + " : " + x1 + " , " + x2);
); 

repeat で80回繰り返します。その都度，前の値を計算後の値を draw(・・・) で2点間を結んで描画面に表示します。青と赤の折れ線ができます。

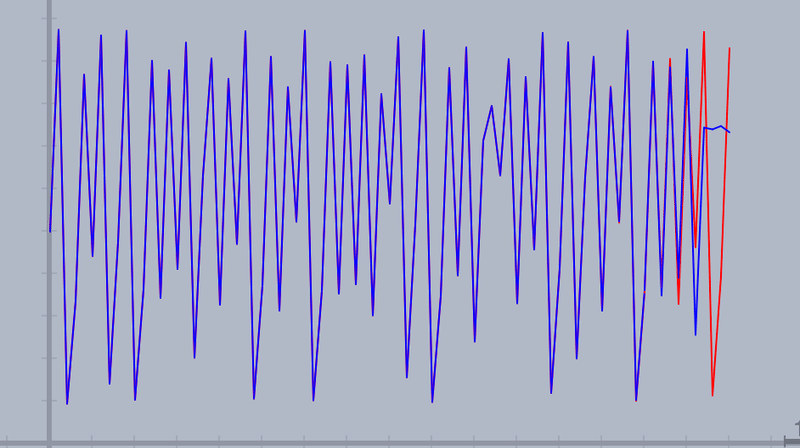
初めのうちは値が同じなので重なりますが，途中から値が変わるので青と赤の線に分かれています。
　また，println(・・・) で，回数と値をコンソールに表示しています。CindyScriptでは，初期状態では小数点以下第4位まで表示するので，63回目で値が異なるのがわかります。
　　　　 println(n+" : "+format(x1,16)+" , "+format(x2,16));
にすると，小数点以下16位まで表示できます。すると，11回目から値が異なります。表示桁をさらに増やすこともできます。次の図は4位まで表示したときと16位まで表示したときのものです。

表計算ソフトの場合もそうですが，計算結果を内部で保持している値と表示する値は同一ではありません。それぞれ四捨五入などで丸めて表示しているので，表示桁数が少ないと見た目は同じになってしまうわけです。

CindyScript にはなじみがなく，Python は知っている，という人のために，Python で処理したものものせておきましょう。同じような結果が得られます。

import numpy as np
import matplotlib.pyplot as plt
n = 80
plt.figure(figsize = (10, 5))
plt.axis([0, n/10, 0, 1])
x = np.linspace(0,n/10,n)
y1 = list(range(1,n+1))
y2 = list(range(1,n+1))
y1[0] = 0.5
y2[0] = 0.5
a = 3.9
for i in range(n-1):
    y1[i+1] = a * y1[i] * (1 - y1[i])
    y2[i+1] = a * y2[i] - a * y2[i] * y2[i]
plt.plot(x, y1, color='r')
plt.plot(x, y2)
plt.show()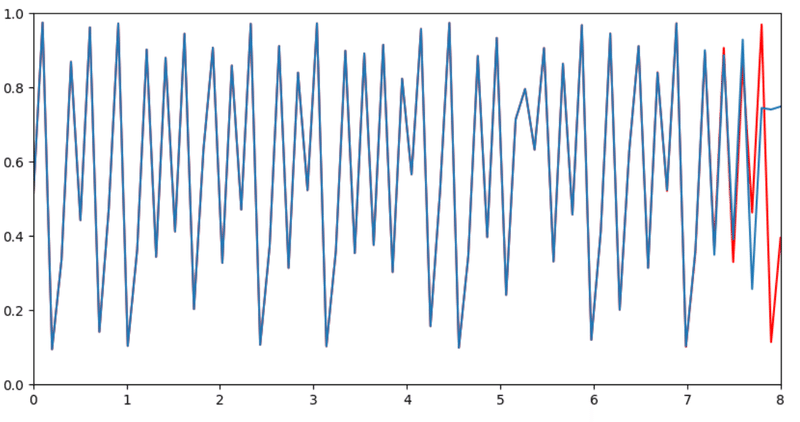

計算誤差とカオスの存在

　以上のように、計算機の結果には誤差がつきまといます。しかし、それは「カオスは存在しない」ということを意味するものではありません。計算機の誤差とは関係なく、「収束しない」「初期値鋭敏性」というものが存在するわけです。それを証明したのが、リー・ヨークです。当時、リー（李）はメリーランド大学の大学院生で、ヨークが指導教官でした。
　リー・ヨークの論文の理解は、高校数学の範疇を超えていますので、一般の人には解析的に（数式処理で）カオスを論じることは無理です。しかし、計算機でカオスをシミュレートするときに、計算機の計算誤差について理解したうえで臨むことは大切です。

誤差対策

　では，計算誤差を回避するにはどうすればよいでしょうか。それは，処理する対象によっていろいろあると言えるでしょう。桁数を切って四捨五入するというのも一つの方法です。
　ここでは，テント写像のリターンマップを例にあげてやってみます。
　テント写像は

　　　$${x_{n+1}= \begin{cases}2x_n \left( 0 \leqq x_n \leqq \dfrac{1}{2} \right)\\ 2(1-x_n) \left( \dfrac{1}{2}< x_n \leqq 1 \right) \end{cases}}$$

で定義されます。
　初期値が 0.1 のとき、値の変化は 0.1 , 0.2 , 0.4 , 0.8 , 0.4 , 0.8 , ・・・ と周期２になります。
　スクリプトは次のようにします。

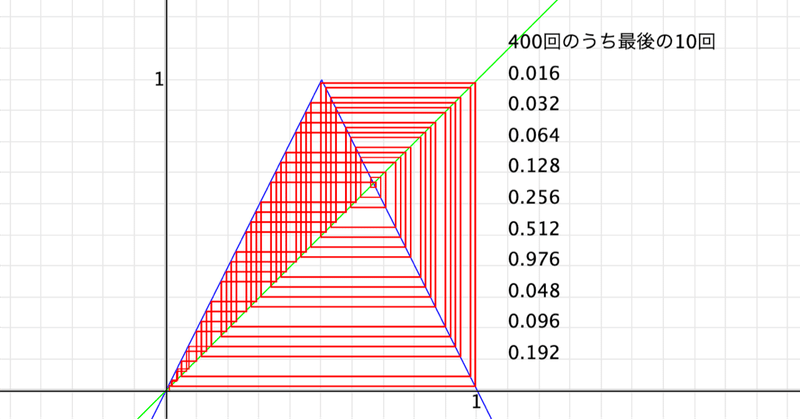
drawtext([0.98, -0.06], 1, size->16);  // 目盛の数字
drawtext([-0.04, 0.98], 1, size->16);
f(x):= if(x < 0.5, 2x, 2(1-x));
plot(f(#));
plot(#, color->[0, 1, 0]);
x = 0.1;
y = 0;
n = 40;
drawtext([1.1,1.1],n+"回のうち最後の10回",size->16);
repeat(n,i,
  draw([x, y], [x, f(x)], color->[1, 0, 0]);
  draw([x, f(x)], [f(x), f(x)], color->[1, 0, 0]);
  if(i > n-10, drawtext([1.1, 0.1 + 0.1*mod(n-i, 10)], x, size->16));
  x = f(x);
  y = x;
);

繰り返し回数が40回のときと60回のときのリターンマップを比較すると次のようになります。
40回では

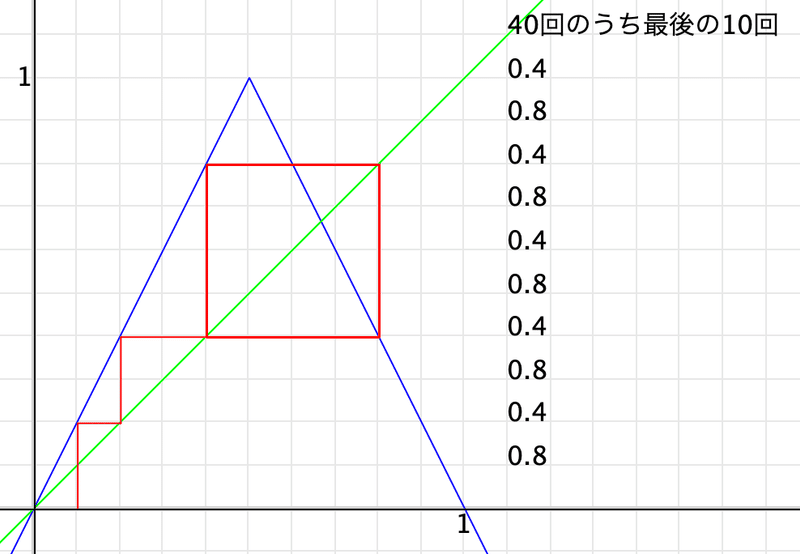
60回では

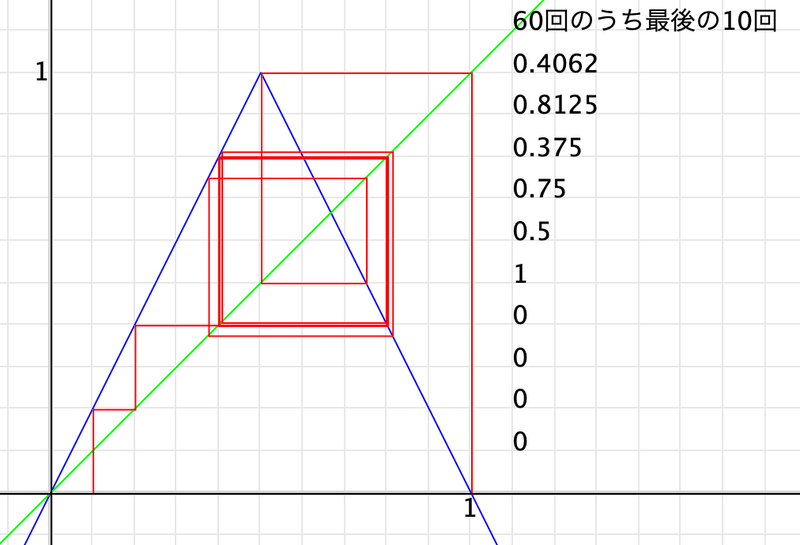
50回くらいでずれたのでしょう、57回目からは０になってしまいました。

　では，対策です。
ロジスティック写像を表計算ソフトで計算した例に戻りましょう。小数点以下16位まで表示しました。2回目以外は右端の数字は０です。計算が合わなくなり始めるのは小数点以下15位くらいの数からです。そこで、小数点以下15位か14位で切ってしまってはどうでしょうか。100000000000000を掛けて小数点の位置を動かしてから四捨五入して戻す、という方法を使います。
スクリプトの
　x=f(x);
を
　x=round(f(x)*100000000000000)/100000000000000;
に変えます。次のようになりました。200回でも大丈夫です。

初期値を 0.09 のように変えても同じような結果になります。x=f(x) だと0になってしまうのが，四捨五入すると周期的になります。
見出し画像は初期値が0.009 の場合の結果です。

←序と目次　に戻る