２次方程式

　２次方程式に関する問題を、２次関数のグラフを利用して考えることがよくあります。
　2次関数のグラフと x 軸との交点の座標は y 座標が０です。グラフ上の点の y 座標は関数の値ですから、2次関数を$${f(x)=ax^2+bx+c}$$ とすると，$${ax^2+bx+c=0}$$ ということになります。この２次方程式の実数解が、x 軸との交点の x 座標になるのです。したがって、２次方程式の実数解の個数や解の範囲についての問題を、グラフを利用して解くことができます。２次方程式の解に関して、グラフを利用するのがもっとも有効な場面は、解の存在範囲の問題でしょう。

【例題】
　２次方程式 $${x^2-2ax-a+2=0}$$ が異なる２つの正の解をもつための定数$${a}$$の値の範囲を求めよ。

　まず、Cinderellaを使って、$${f(x)=x^2-2ax-a+2}$$ のグラフを描き、状況を把握することにします。定数$${a}$$の値は、「スライダ」で変化させます。
　まず、スライダを作図します。磁石ツール（グリッドにスナップする）で軸と方眼を表示しておき、線分を加えるツールで適当なところに線分をとります。次に、点を加えるツールで線分上に点をとります。線分はAB、点はCになるはずです。点AとCの距離は |A, C| で計算できるので、これを利用して値を設定します。スクリプトエディタを開いて、Drawスロットに次のスクリプトを書きます。

　　　　　　　a = |A, C| - 3;

ここでは、Cが左端(A)にあるとき、$${a=-3}$$  となるようにしました。問題の状況に応じて適当に変えることにします。
 　drawtext(C.xy-[0,1],"a="+a,size -> 16,align -> "mid");
で$${a}$$の値を点Cの下に表示しておきましょう。また，判別式 $${D=a^2+a-2}$$ の値もその下に表示しておきます。

f(x):= x^2 - 2*a*x - a + 2;
a = |A, C| - 3;
drawtext(C.xy-[0, 1], "a="+a,size -> 16, align -> "mid");
drawtext(C.xy-[0, 2], "D="+(a^2+a-2), size -> 16, align -> "mid");
drawtext([6, 4], "$f(x)=x^2-2ax-a+2$", size -> 16);
plot(f(x));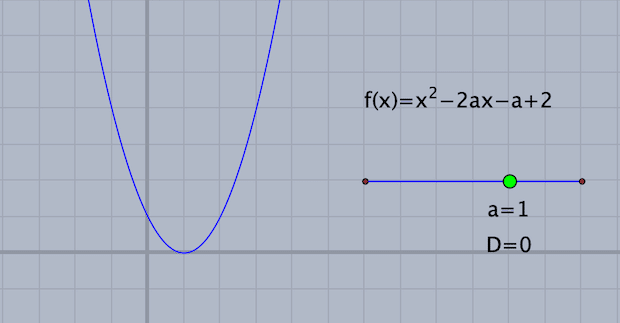

　動かすモードにして、スライダ上の点Cをドラッグすると、放物線の位置が変わります。「異なる２つの正の解をもつ」ということは、x軸の正の部分の２ヶ所で交わるということです。そのような$${a}$$の値の範囲を求めてみると、$${1<a<2}$$ であることがわかります。

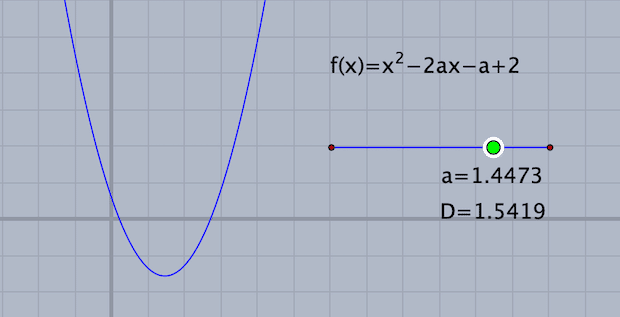
　では、これをどのように計算して求めればよいでしょうか。いいかえると、どのような条件式を立てればよいでしょうか。
　そのためには、「x軸の正の部分の２ヶ所で交わる」ための条件を探し出すわけですが、これが結構難しいのです。教科書などではいきなり条件を挙げていますが、なぜその条件になるのか，理由がわからなければ結局は解けるようにはなりません。いくつか想定しながらスライダを動かしてみましょう。

(1) 頂点の位置はどうか。
(2) 軸の位置はどうか。
　これは頂点のｘ座標と同じですが、(1)ではx軸と交わるかどうか、つまり頂点のy座標（縦方向に注目していくことになるので、こちらでは横方向に注目してみます。
(3)「正の」という条件はどのように考えればよいか。

これらのことを，インタラクティブに頭を動かしながら考察していくわけです。とはいえ，そう簡単ではありません。
　まず、(1)ですが、頂点がx軸より下方になければいけないことはもちろんです。前述の、判別式と関係してきます。D>0です。これだけでは決まらないことはすぐわかるでしょう。
　(2)の軸の位置をみてみましょう。スクリプトを１行増やして，軸を破線で表示することにします。
  draw(join([a, 0], [a, 1]), dashtype -> 2);
　すると、軸はy軸より右になければいけないことはわかるでしょう。しかし、次図のように、軸がy軸より右にあるだけでは条件は満たさないということもよくわかります。

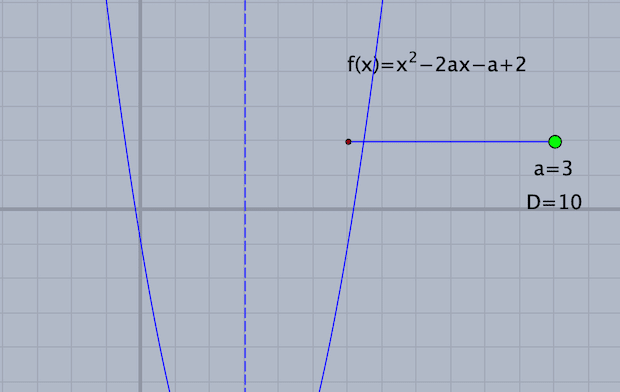
　頂点が下の方に行き過ぎると、原点より下でy軸と交わるので条件を満たさないわけです。すると、(3)の「正の」という条件は、「原点より上でy軸と交わる」ことになります。
　こうして条件を拾い出すようにすれば、問題が「異なる２つの負の解」「異符号の解」「０以上３以下の解」のように変わっても応用ができます。
　整理すると、次の３つの条件を調べていけばよいことになります。

　(1) 判別式 D > 0
　(2) 軸の位置
　(3) 定義域における端点での関数値の正負

　しかし、これを暗記するだけではやはりだめで、頭の中に図がないと解けるようにはなりません。そのためには，いろいろな状況を想定して条件を絞り込んでいくという作業を実際にやってみることが必要なのです。教科書や問題集にある練習問題を、Cinderellaで実際に動かしてみると状況が理解できるようになるでしょう。

２次不等式

　２次不等式 $${ax^2+bx+c>0}$$ の解は，$${f(x)=ax^2+bx+c}$$ のグラフがx軸より上にあるxの範囲，$${ax^2+bx+c<0}$$ の解は，$${f(x)=ax^2+bx+c}$$ のグラフがx軸より下にあるxの範囲，です。これは，２次方程式の解とグラフの位置関係を見たときから一歩発展して考えます。このことは，２次不等式だけでなく，３次不等式や三角関数の不等式でも同じように考えられます。

【例題】
　２次不等式 $${x^2-2ax-a+2>0}$$ がすべての実数$${x}$$ に対して成り立つように定数$${a}$$ の値の範囲を求めよ。

　これは，先ほどの２次方程式の例題で使ったグラフで考えれば状況はすぐにわかるでしょう。グラフ全体が$${x}$$軸より上方にあるときの$${a}$$ の値の範囲です。条件は判別式だけでよいことがわかります。
　「すべての実数」ではなく、範囲を限定すると少し難しくなります。

【例題】
　２次不等式 $${x^2-2ax-a+2>0}$$ が，$${0 \leqq x \leqq 2}$$ のとき常に成り立つように定数$${a}$$ の値の範囲を求めよ。

　こんどは、判別式だけでは決定できません。
　前節の、２次方程式の解の存在範囲で考えたことを思い出すと、軸の位置がポイントであることがわかるでしょう。さらに、定数$${a}$$の値を変化させたとき、放物線がどのように動くかまで理解しておくと状況把握も楽になります。
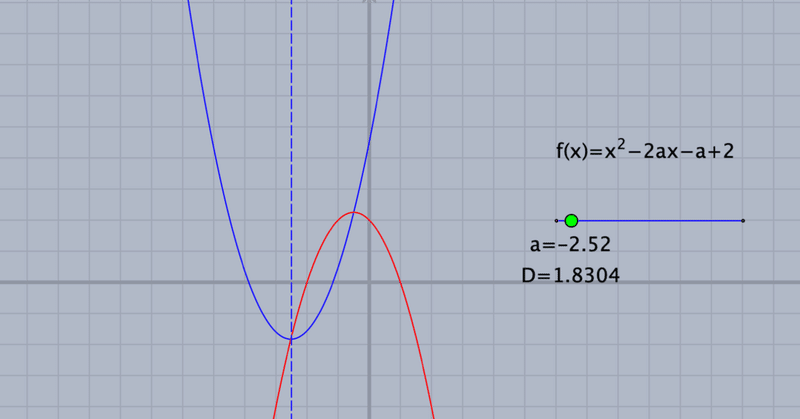
　放物線の頂点の座標は$${(a,-a^2-a+2)}$$ です。$${x=a,y=-a^2-a+2}$$ から$${a}$$ を消去すると $${y=-x^2-x+2}$$ となります。このことは，$${f(x)=x^2-2ax-a+2}$$ のグラフの頂点がこの放物線上にあることを示しています。前の図に，plot(-x^2-x+2,color->[1,0,0]);　を追加して，スライダを動かしてみましょう。頂点がこの赤い放物線上を動くことがわかります。

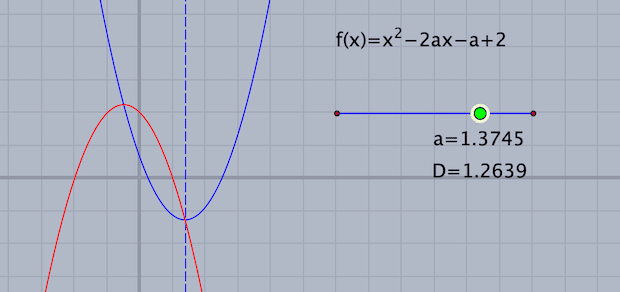
　このイメージができると，$${0 \leqq x \leqq 2}$$ のとき常に成り立つための条件も拾いやすくなります。

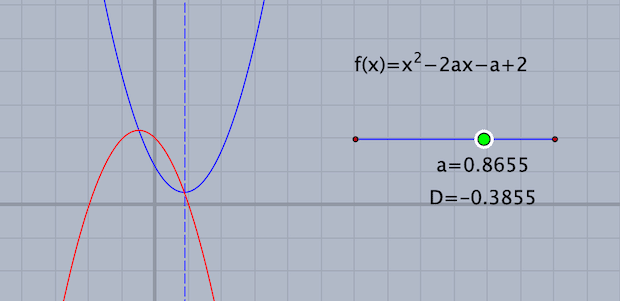
　教科書では，いきなり条件を挙げていて，ここまではやっていません。しかし，このイメージを持つことは，問題を解く上でおおきな手助けになります。

← Cinderella で数学・情報　に戻る