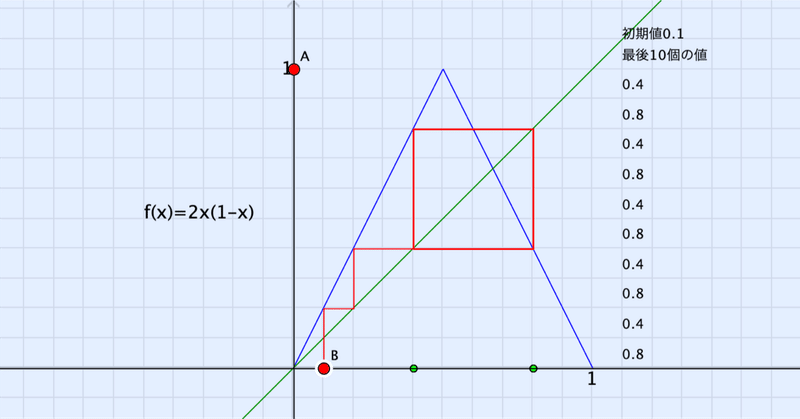
Cinderellaでカオスを描く:パイこね変換
カオスというと必ず出てくるのが「パイこね変換」です。しかし、私は最初に「Excelで学ぶ理工系シミュレーション入門」(臼田昭司他 CQ出版社)で見たときに、どういう意味があるのかさっぱりわかりませんでした。のばしてたたんで、断面がカオス?
山口昌哉著「カオスとフラクタル」(ちくま学芸文庫(前ブルーバックス))には詳しく書いてあり、少しわかりました。ここから図を引用して、関数との関係を示しましょう。
次の図は,パイの材料を「上から押さえてのばし」「半分に切って」「重ねた」ものです。重ねるときに,左はそのままの向きで,右は向きを変えたものです。
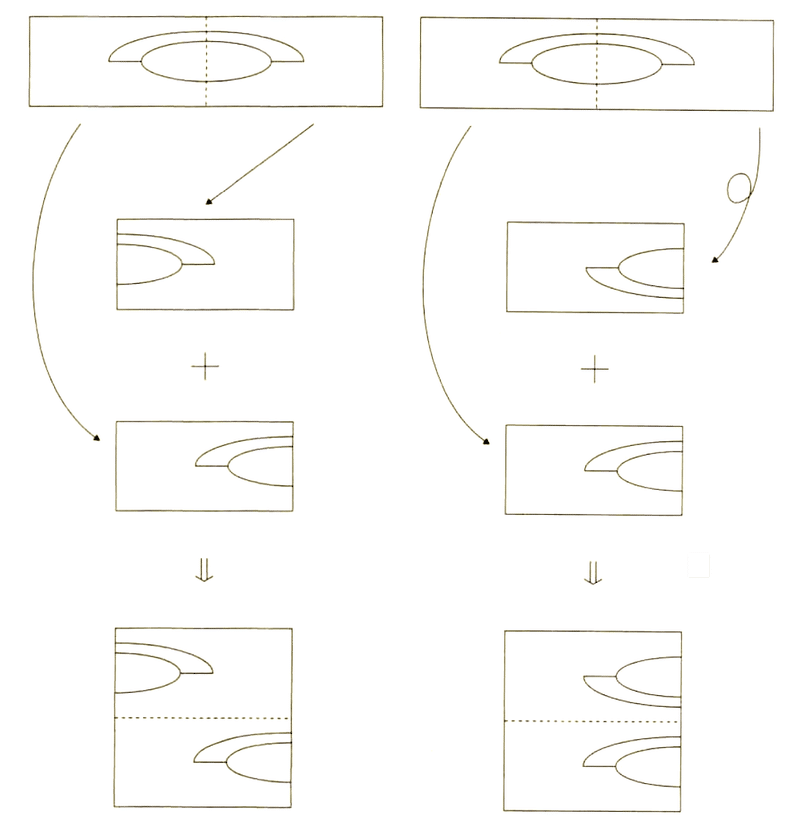
半分に切ったので横幅が半分になりますが,これを横に「引き伸ばして」初めと同じ幅にします。同書ではこのあと長い説明が続きますが,そこは省略して,この2つのパターンに相当する2つの関数を次のように定義します。(詳しくは同書または類書をごらんください)
$${f(x)=\begin{cases}2x \left(0 \leqq x \leqq \dfrac{1}{2} \right) \\ 2x-1 \left(\dfrac{1}{2} < x \leqq 1 \right)\end{cases}}$$
$${g(x)=\begin{cases}2x \left(0 \leqq x \leqq \dfrac{1}{2} \right) \\ 2(1-x) \left(\dfrac{1}{2} < x \leqq 1 \right)\end{cases}}$$
$${f(x)}$$ をベルヌーイ写像,$${g(x)}$$ をテント写像といいます。
この関数を用いて、ある値を変換していくのです。たとえば、0.2から出発するとベルヌーイ写像では 0.2 , f(0.2)=0.4 , f(0.4)=0.8 , f(0.8)=0.6 , f(0.6)=0.2 , 以下、0.4 , 0.8 , 0.6 , ・・・・ となっていきます。
テント写像では 0.2 , 0.4 , 0.8 , 0.4 , 0.8 , 0.4 , 0.8 , 0.4 , ・・・・ となっていきます。
このリターンマップを描いてみましょう。(リターンマップについては「ロジスティック写像」を参照してください)
左がベルヌーイ写像、右がテント写像です。繰り返しは200回行っていますが,ベルヌーイ写像では周期4,テント写像では周期2で繰り返すようになります。
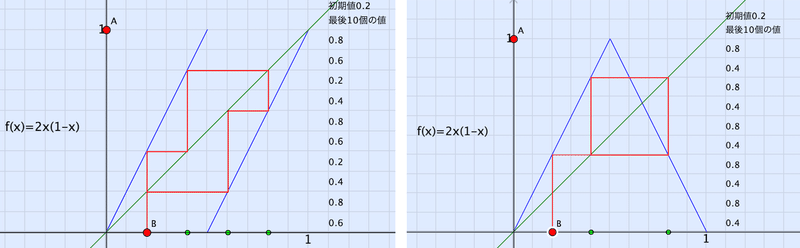
初期値をわずかに増やして 0.2001にすると,次のようになります。
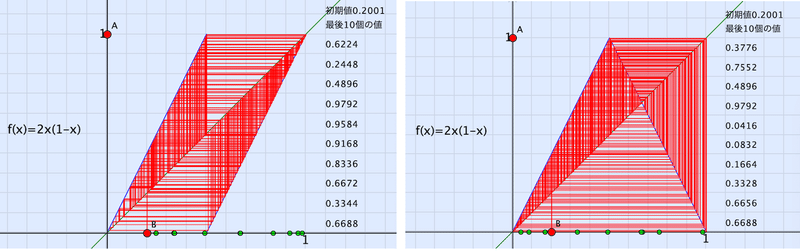
値の動きがばらばらになりました。これが、カオスの初期値鋭敏性です。
しかし、本当にカオスなのか? カオスだから初期値鋭敏性が出ているのか、という疑問は残ります。この疑問にきちんと答えるためには、解析的に(数式処理をして)リー・ヨークの定理が成り立つかどうかとか、リアプノフ指数が正かどうかとかを検証しなければなりませんが、ここは高校数学の範疇を超えるのでパスして、周期倍分岐図を描くことで納得することにしましょう。さきほどの関数で,係数2を$${a}$$として,次のように定義します。
$${f(x)=\begin{cases}ax \left(0 \leqq x \leqq \dfrac{1}{2} \right) \\ a(x-\dfrac{1}{2}) \left(\dfrac{1}{2} < x \leqq 1 \right)\end{cases}}$$
$${g(x)=\begin{cases}ax \left(0 \leqq x \leqq \dfrac{1}{2} \right) \\ a(1-x) \left(\dfrac{1}{2} < x \leqq 1 \right)\end{cases}}$$
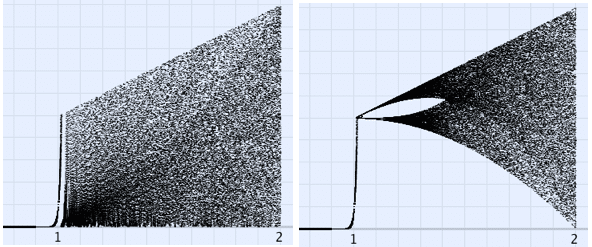
似たような関数ですが、周期倍分岐図を描いて見るとまったく様相が違うことがわかります。
では,Cinderella でこれらの図を描く方法を簡単に説明しましょう。作図ツールで,点A,B をとり,座標軸も直線を加えるツールで描いておきます。
リターンマップのスクリプトは次のようになっています。
ca = A.y*2;
B.x = 0.2;//f(x):= if(x < 0.5, cax, ca(1 - x)); // テント
f(x):= if(x < 0.5, cax, ca(x - 1/2)); // ベルヌーイplot(f(#), start->0, stop->1);
plot(#, color->[0, 0.5, 0]);
drawtext([-0.5, 0.5],"f(x)=" + ca + "x(1-x)", size->16);
drawtext([0.98, -0.06], 1, size->16);
drawtext([-0.04, 0.98], 1, size->16);
drawtext([1.1, 1.1], "初期値" + B.x, size->12);
drawtext([1.1, 1.03], "最後10個の値");
x = B.x;
y = 0;
n = 200;
linecolor([1, 0, 0]);
repeat(n, i,
println(format(x, 4));
if(i > n - 10,
drawtext([1.1, (n-i)*0.1 + 0.03],format(x, 5), size->12);
);
draw([x, y], [x, f(x)]);
draw([x, f(x)], [f(x), f(x)]);
x = round(f(x)*1000000)/1000000;
y = x;
if(i > n - 10, draw([x,0], color->[0, 1, 0], size->3));
);周期倍分岐図のほうは次のようになっています。こちらは繰り返し回数が多いので実行に時間がかかりますのでそのつもりで。
f(a,x):= if(x < 0.5, ax, a(x - 1/2)); // ベルヌーイ
//f(a,x):= if(x < 0.5, ax, a(1 - x)); // テント
a = 0;
x0 = 0.1;
repeat(2000,
a = a + 0.001;
x = x0;
repeat(100,x = f(a,x));
repeat(60,
x = f(a, x);
draw([a, x], size->0.05);
);
);
// a軸目盛表示
apply(0..4, drawtext([#-0.02, -0.07], #, size->16));